 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
L'inférence variationnelle (VI) présente l'inférence bayésienne approximative comme un problème d'optimisation et recherche une distribution postérieure « de substitution » qui minimise la divergence KL avec la vraie postérieure. Le VI basé sur le gradient est souvent plus rapide que les méthodes MCMC, se compose naturellement avec l'optimisation des paramètres du modèle et fournit une limite inférieure sur la preuve du modèle qui peut être utilisée directement pour la comparaison de modèles, le diagnostic de convergence et l'inférence composable.
TensorFlow Probability propose des outils pour des VIs rapides, flexibles et évolutifs qui s'intègrent naturellement dans la pile TFP. Ces outils permettent de construire des a posteriori de substitution avec des structures de covariance induites par des transformations linéaires ou des flux de normalisation.
VI peut être utilisé pour estimer bayésienne intervalles crédibles pour les paramètres d'un modèle de régression pour estimer les effets des différents traitements ou les caractéristiques observées sur un résultat d'intérêt. Des intervalles crédibles limitent les valeurs d'un paramètre non observé avec une certaine probabilité, selon la distribution postérieure du paramètre conditionnée sur les données observées et étant donné une hypothèse sur la distribution a priori du paramètre.
Dans ce Colab, nous montrons comment utiliser VI pour obtenir des intervalles crédibles pour les paramètres d'un modèle de régression bayésienne linéaires pour les niveaux de radon mesurés dans les foyers ( en utilisant Gelman et al de (2007) ensemble de données Radon. , Voir des exemples similaires à Stan). Nous montrons comment TFP JointDistribution s se combinent avec bijectors pour construire et installer deux types de substitution de dents postérieures expressives:
- une distribution normale standard transformée par une matrice de blocs. La matrice peut refléter l'indépendance entre certaines composantes de la postérieure et la dépendance parmi d'autres, relâchant l'hypothèse d'une postérieure à champ moyen ou à covariance complète.
- un plus complexe, de plus grande capacité inverse écoulement autorégressif .
Les postérieurs de substitution sont entraînés et comparés aux résultats d'une ligne de base postérieure de substitution à champ moyen, ainsi qu'à des échantillons de vérité terrain de l'hamiltonien Monte Carlo.
Présentation de l'inférence variationnelle bayésienne
Supposons que nous ayons le processus génératif suivant, où \(\theta\) représente des paramètres aléatoires, \(\omega\) représente les paramètres déterministes et les \(x_i\) sont caractéristiques et les \(y_i\) sont des valeurs cibles pour \(i=1,\ldots,n\) points de données observées: \ begin {align } &\theta \sim r(\Theta) && \text{(Prior)}\ &\text{for } i = 1 \ldots n: \nonumber \ &\quad y_i \sim p(Y_i|x_i, \theta , \ omega) && \ texte {(probabilité)} \ end {align}
VI est alors caractérisé par : $\newcommand{\E}{\operatorname{\mathbb{E} } } \newcommand{\K}{\operatorname{\mathbb{K} } } \newcommand{\defeq}{\overset {\tiny\text{def} }{=} } \DeclareMathOperator*{\argmin}{arg\,min}$
\ begin {align} - \ log p ({y_i} _i ^ n | {x_i} _i ^ n, \ omega) et \ defeq - \ log \ int \ textrm {d} \ theta \, r (\ theta) \ prod_i^np(y_i|x_i,\theta, \omega) && \text{(Intégrale vraiment difficile)} \ &= -\log \int \textrm{d}\theta\, q(\theta) \frac{1 }{q(\theta)} r(\theta) \prod_i^np(y_i|x_i,\theta, \omega) && \text{(Multiplier par 1)}\ &\le - \int \textrm{d} \ theta \, q (\ theta) \ log \ frac {r (\ theta) \ prod_i ^ np (y_i | x i, \ theta, \ omega)} {q (\ theta)} && \ texte {(inégalité de Jensen )} \ & \ defeq \ E {q (\ theta)} [- \ log p (y_i | x_i, \ theta, \ omega)] + \ K [q (\ theta), r (\ theta)] \ & \ defeq \text{expected negative log likelihood"} + - \text{expected negative log likelihood"} + \ texte {kl régularisateur"} \ end {align}
(Techniquement Nous supposons que \(q\) est absolument continue par rapport à \(r\). Voir aussi, l'inégalité de Jensen .)
Puisque la borne est valable pour tout q, elle est évidemment la plus stricte pour :
\[q^*,w^* = \argmin_{q \in \mathcal{Q},\omega\in\mathbb{R}^d} \left\{ \sum_i^n\E_{q(\Theta)}\left[ -\log p(y_i|x_i,\Theta, \omega) \right] + \K[q(\Theta), r(\Theta)] \right\}\]
Concernant la terminologie, on appelle
- \(q^*\) le "postérieur de substitution" et,
- \(\mathcal{Q}\) la "famille de substitution."
\(\omega^*\) représente les valeurs maximum de vraisemblance des paramètres déterministes sur la perte VI. Voir cette enquête pour plus d' informations sur l' inférence variationnelle.
Exemple : Régression linéaire hiérarchique bayésienne sur les mesures de Radon
Le radon est un gaz radioactif qui pénètre dans les maisons par des points de contact avec le sol. C'est un cancérogène qui est la principale cause de cancer du poumon chez les non-fumeurs. Les niveaux de radon varient considérablement d'un foyer à l'autre.
L'EPA a fait une étude des niveaux de radon dans 80 000 maisons. Deux prédicteurs importants sont :
- Étage sur lequel la mesure a été prise (radon plus élevé dans les sous-sols)
- Niveau d'uranium du comté (corrélation positive avec les niveaux de radon)
Prédire les niveaux de radon dans les maisons groupées par comté est un problème classique dans la modélisation hiérarchique bayésienne, introduite par Gelman et Hill (2006) . Nous construirons un modèle linéaire hiérarchique pour prédire les mesures de radon dans les maisons, dans lequel la hiérarchie est le regroupement des maisons par comté. Nous nous intéressons à des intervalles crédibles pour l'effet de l'emplacement (comté) sur le niveau de radon des maisons au Minnesota. Afin d'isoler cet effet, les effets du plancher et du niveau d'uranium sont également inclus dans le modèle. De plus, nous incorporerons un effet contextuel correspondant à l'étage moyen sur lequel la mesure a été prise, par comté, de sorte que s'il y a une variation entre les comtés de l'étage sur lequel les mesures ont été prises, cela ne soit pas attribué à l'effet de comté.
pip3 install -q tf-nightly tfp-nightly
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
import warnings
tfd = tfp.distributions
tfb = tfp.bijectors
plt.rcParams['figure.facecolor'] = '1.'
# Load the Radon dataset from `tensorflow_datasets` and filter to data from
# Minnesota.
dataset = tfds.as_numpy(
tfds.load('radon', split='train').filter(
lambda x: x['features']['state'] == 'MN').batch(10**9))
# Dependent variable: Radon measurements by house.
dataset = next(iter(dataset))
radon_measurement = dataset['activity'].astype(np.float32)
radon_measurement[radon_measurement <= 0.] = 0.1
log_radon = np.log(radon_measurement)
# Measured uranium concentrations in surrounding soil.
uranium_measurement = dataset['features']['Uppm'].astype(np.float32)
log_uranium = np.log(uranium_measurement)
# County indicator.
county_strings = dataset['features']['county'].astype('U13')
unique_counties, county = np.unique(county_strings, return_inverse=True)
county = county.astype(np.int32)
num_counties = unique_counties.size
# Floor on which the measurement was taken.
floor_of_house = dataset['features']['floor'].astype(np.int32)
# Average floor by county (contextual effect).
county_mean_floor = []
for i in range(num_counties):
county_mean_floor.append(floor_of_house[county == i].mean())
county_mean_floor = np.array(county_mean_floor, dtype=log_radon.dtype)
floor_by_county = county_mean_floor[county]
Le modèle de régression est spécifié comme suit :
\(\newcommand{\Normal}{\operatorname{\sf Normal} }\)\ begin {align} & \ text {uranium_weight} \ sim \ Normal (0, 1) \ & \ text {county_floor_weight} \ sim \ Normal (0, 1) \ & \ text {for} j = 1 \ ldots \text{num_counties}:\ &\quad \text{county_effect}_j \sim \Normal (0, \sigma_c)\ &\text{for } i = 1\ldots n:\ &\quad \mu_i = ( \ & \ quad \ quad \ text {biais} \ & \ quad \ quad + \ texte {effet du comté} {\ texte {comté} _i} \ & \ quad \ quad + \ texte {log_uranium} _i \ texte de fois {uranium_weight } \ & \ quad \ quad + \ texte {floor_of_house} _i \ texte de fois {de floor_weight} \ & \ quad \ quad + \ texte {comté floor_by} {\ texte {comté} _i} \ texte de fois {county_floor_weight}) \ & \ quad \ text {log_radon} _i \ sim \ normal (\ mu_i, \ sigma_y) \ end {align} dans lequel \(i\) indexe les observations et \(\text{county}_i\) est le comté où le \(i\)e observation était pris.
Nous utilisons un effet aléatoire au niveau du comté pour capturer la variation géographique. Les paramètres uranium_weight et county_floor_weight sont modélisés de façon probabiliste et floor_weight et la constante de bias sont déterministes. Ces choix de modélisation sont largement arbitraires et sont faits dans le but de démontrer VI sur un modèle probabiliste de complexité raisonnable. Pour une discussion plus approfondie de la modélisation multi - niveaux avec fixes et des effets aléatoires dans TFP, en utilisant l'ensemble de données de radon, voir multiniveau Modélisation Primaire et Fitting linéaires généralisés effets mixtes modèles utilisant Variational Inference .
# Create variables for fixed effects.
floor_weight = tf.Variable(0.)
bias = tf.Variable(0.)
# Variables for scale parameters.
log_radon_scale = tfp.util.TransformedVariable(1., tfb.Exp())
county_effect_scale = tfp.util.TransformedVariable(1., tfb.Exp())
# Define the probabilistic graphical model as a JointDistribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
uranium_weight = yield tfd.Normal(0., scale=1., name='uranium_weight')
county_floor_weight = yield tfd.Normal(
0., scale=1., name='county_floor_weight')
county_effect = yield tfd.Sample(
tfd.Normal(0., scale=county_effect_scale),
sample_shape=[num_counties], name='county_effect')
yield tfd.Normal(
loc=(log_uranium * uranium_weight + floor_of_house* floor_weight
+ floor_by_county * county_floor_weight
+ tf.gather(county_effect, county, axis=-1)
+ bias),
scale=log_radon_scale[..., tf.newaxis],
name='log_radon')
# Pin the observed `log_radon` values to model the un-normalized posterior.
target_model = model.experimental_pin(log_radon=log_radon)
Postérieurs de substitution expressifs
Ensuite, nous estimons les distributions postérieures des effets aléatoires à l'aide de VI avec deux types différents de postérieurs de substitution :
- Une distribution normale multivariée contrainte, avec une structure de covariance induite par une transformation matricielle par blocs.
- Une distribution à plusieurs variables standard normale transformée par un inverse Autoregressive de flux , qui est ensuite divisé et restructuré pour correspondre à l'appui de la partie postérieure.
Multivariée Normale mère porteuse postérieure
Pour construire ce postérieur de substitution, un opérateur linéaire pouvant être entraîné est utilisé pour induire une corrélation entre les composants du postérieur.
# Determine the `event_shape` of the posterior, and calculate the size of each
# `event_shape` component. These determine the sizes of the components of the
# underlying standard Normal distribution, and the dimensions of the blocks in
# the blockwise matrix transformation.
event_shape = target_model.event_shape_tensor()
flat_event_shape = tf.nest.flatten(event_shape)
flat_event_size = tf.nest.map_structure(tf.reduce_prod, flat_event_shape)
# The `event_space_bijector` maps unconstrained values (in R^n) to the support
# of the prior -- we'll need this at the end to constrain Multivariate Normal
# samples to the prior's support.
event_space_bijector = target_model.experimental_default_event_space_bijector()
Construire un JointDistribution à la norme multivaluée composants normaux, avec des tailles déterminées par les composants correspondants avant. Les composants doivent être à valeur vectorielle afin qu'ils puissent être transformés par l'opérateur linéaire.
base_standard_dist = tfd.JointDistributionSequential(
[tfd.Sample(tfd.Normal(0., 1.), s) for s in flat_event_size])
Construisez un opérateur linéaire triangulaire inférieur entraînable. Nous l'appliquerons à la distribution normale standard pour implémenter une transformation matricielle par blocs (entrainable) et induire la structure de corrélation du postérieur.
Au sein de l'opérateur linéaire séquencée, un bloc complet matrice trainable représente pleine covariance entre deux composantes de la partie postérieure, alors qu'un bloc de zéros (ou None ) exprime son indépendance. Les blocs sur la diagonale sont des matrices triangulaires inférieures ou diagonales, de sorte que la structure entière du bloc représente une matrice triangulaire inférieure.
L'application de ce bijecteur à la distribution de base donne une distribution normale multivariée avec une moyenne de 0 et une covariance (factorisée de Cholesky) égale à la matrice de blocs triangulaire inférieur.
operators = (
(tf.linalg.LinearOperatorDiag,), # Variance of uranium weight (scalar).
(tf.linalg.LinearOperatorFullMatrix, # Covariance between uranium and floor-by-county weights.
tf.linalg.LinearOperatorDiag), # Variance of floor-by-county weight (scalar).
(None, # Independence between uranium weight and county effects.
None, # Independence between floor-by-county and county effects.
tf.linalg.LinearOperatorDiag) # Independence among the 85 county effects.
)
block_tril_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
scale_bijector = tfb.ScaleMatvecLinearOperatorBlock(block_tril_linop)
Après l' application de l'opérateur linéaire à la norme distribution normale, appliquer une multipart Shift bijector pour permettre la moyenne de prendre des valeurs non nulles.
loc_bijector = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
La distribution normale multivariée résultante, obtenue en transformant la distribution normale standard avec les bijecteurs d'échelle et d'emplacement, doit être remodelée et restructurée pour correspondre à la priorite, et finalement contrainte au support de la prior.
# Reshape each component to match the prior, using a nested structure of
# `Reshape` bijectors wrapped in `JointMap` to form a multipart bijector.
reshape_bijector = tfb.JointMap(
tf.nest.map_structure(tfb.Reshape, flat_event_shape))
# Restructure the flat list of components to match the prior's structure
unflatten_bijector = tfb.Restructure(
tf.nest.pack_sequence_as(
event_shape, range(len(flat_event_shape))))
Maintenant, mettez le tout ensemble - chaînez les bijecteurs pouvant être entraînés ensemble et appliquez-les à la distribution normale standard de base pour construire le postérieur de substitution.
surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
loc_bijector, # allow for nonzero mean
scale_bijector # apply the block matrix transformation to the standard Normal distribution
]))
Former le substitut postérieur normal multivarié.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
mvn_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mvn_samples = surrogate_posterior.sample(1000)
mvn_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mvn_samples)
- surrogate_posterior.log_prob(mvn_samples))
print('Multivariate Normal surrogate posterior ELBO: {}'.format(mvn_final_elbo))
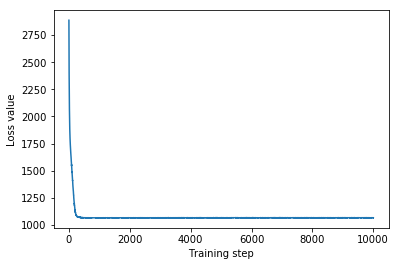
plt.plot(mvn_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Multivariate Normal surrogate posterior ELBO: -1065.705322265625
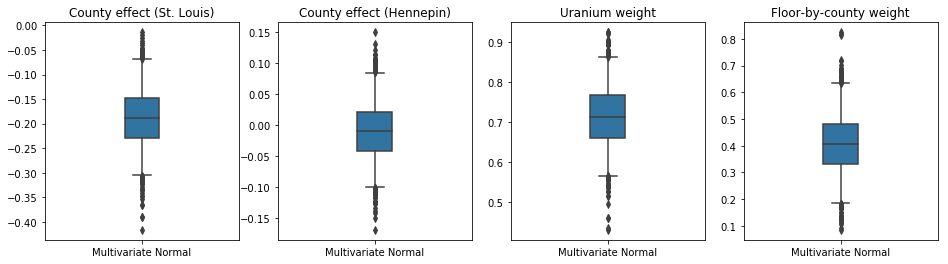
Étant donné que le substitut a posteriori formé est une distribution TFP, nous pouvons en prélever des échantillons et les traiter pour produire des intervalles crédibles postérieurs pour les paramètres.
La boîte et moustaches courbes montrent en dessous de 50% et 95% des intervalles crédibles pour l'effet du comté des deux plus grands comtés et les coefficients de régression sur les mesures d'uranium dans le sol et le plancher moyen par comté. Les intervalles de crédibilité postérieurs pour les effets de comté indiquent que l'emplacement dans le comté de St. Louis est associé à des niveaux de radon inférieurs, après prise en compte d'autres variables, et que l'effet de l'emplacement dans le comté de Hennepin est presque neutre.
Les intervalles postérieurs crédibles sur les poids de régression montrent que des niveaux plus élevés d'uranium dans le sol sont associés à des niveaux plus élevés de radon, et les comtés où les mesures ont été prises aux étages supérieurs (probablement parce que la maison n'avait pas de sous-sol) ont tendance à avoir des niveaux plus élevés de radon, qui pourraient se rapporter aux propriétés du sol et à leur effet sur le type de structures construites.
Le coefficient (déterministe) du plancher est négatif, indiquant que les étages inférieurs ont des niveaux de radon plus élevés, comme prévu.
st_louis_co = 69 # Index of St. Louis, the county with the most observations.
hennepin_co = 25 # Index of Hennepin, with the second-most observations.
def pack_samples(samples):
return {'County effect (St. Louis)': samples.county_effect[..., st_louis_co],
'County effect (Hennepin)': samples.county_effect[..., hennepin_co],
'Uranium weight': samples.uranium_weight,
'Floor-by-county weight': samples.county_floor_weight}
def plot_boxplot(posterior_samples):
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
# Invert the results dict for easier plotting.
k = list(posterior_samples.values())[0].keys()
plot_results = {
v: {p: posterior_samples[p][v] for p in posterior_samples} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
sns.boxplot(data=list(var_results.values()), ax=axes[i],
width=0.18*len(var_results), whis=(2.5, 97.5))
# axes[i].boxplot(list(var_results.values()), whis=(2.5, 97.5))
axes[i].title.set_text(var)
fs = 10 if len(var_results) < 4 else 8
axes[i].set_xticklabels(list(var_results.keys()), fontsize=fs)
results = {'Multivariate Normal': pack_samples(mvn_samples)}
print('Bias is: {:.2f}'.format(bias.numpy()))
print('Floor fixed effect is: {:.2f}'.format(floor_weight.numpy()))
plot_boxplot(results)
Bias is: 1.40 Floor fixed effect is: -0.72
Substitut de flux autorégressif inverse postérieur
Les flux autorégressifs inverses (IAF) sont des flux de normalisation qui utilisent des réseaux de neurones pour capturer des dépendances complexes et non linéaires entre les composants de la distribution. Ensuite, nous construisons un modèle a posteriori de substitution IAF pour voir si ce modèle à capacité plus élevée et plus flexible surpasse le modèle normal multivarié contraint.
# Build a standard Normal with a vector `event_shape`, with length equal to the
# total number of degrees of freedom in the posterior.
base_distribution = tfd.Sample(
tfd.Normal(0., 1.), sample_shape=[tf.reduce_sum(flat_event_size)])
# Apply an IAF to the base distribution.
num_iafs = 2
iaf_bijectors = [
tfb.Invert(tfb.MaskedAutoregressiveFlow(
shift_and_log_scale_fn=tfb.AutoregressiveNetwork(
params=2, hidden_units=[256, 256], activation='relu')))
for _ in range(num_iafs)
]
# Split the base distribution's `event_shape` into components that are equal
# in size to the prior's components.
split = tfb.Split(flat_event_size)
# Chain these bijectors and apply them to the standard Normal base distribution
# to build the surrogate posterior. `event_space_bijector`,
# `unflatten_bijector`, and `reshape_bijector` are the same as in the
# multivariate Normal surrogate posterior.
iaf_surrogate_posterior = tfd.TransformedDistribution(
base_distribution,
bijector=tfb.Chain([
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the prior
reshape_bijector, # reshape the vector-valued components to match the shapes of the prior components
split] + # Split the samples into components of the same size as the prior components
iaf_bijectors # Apply a flow model to the Tensor-valued standard Normal distribution
))
Former la mère porteuse IAF postérieure.
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
iaf_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
iaf_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=4,
jit_compile=True)
iaf_samples = iaf_surrogate_posterior.sample(1000)
iaf_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*iaf_samples)
- iaf_surrogate_posterior.log_prob(iaf_samples))
print('IAF surrogate posterior ELBO: {}'.format(iaf_final_elbo))
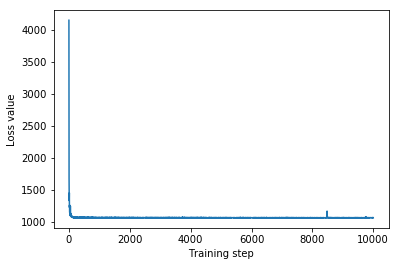
plt.plot(iaf_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
IAF surrogate posterior ELBO: -1065.3663330078125
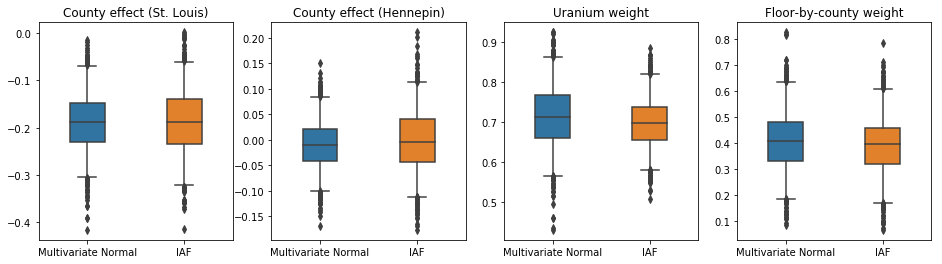
Les intervalles crédibles pour l'IAF a posteriori de substitution semblent similaires à ceux de la normale multivariée contrainte.
results['IAF'] = pack_samples(iaf_samples)
plot_boxplot(results)
Ligne de base : champ moyen de substitution a posteriori
Les variables postérieures de substitution VI sont souvent supposées être des distributions normales à champ moyen (indépendantes), avec des moyennes et des variances entraînables, qui sont contraintes à la prise en charge de la priorité par une transformation bijective. Nous définissons un substitut postérieur à champ moyen en plus des deux substituts postérieurs plus expressifs, en utilisant la même formule générale que le postérieur normal multivarié de substitution.
# A block-diagonal linear operator, in which each block is a diagonal operator,
# transforms the standard Normal base distribution to produce a mean-field
# surrogate posterior.
operators = (tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag)
block_diag_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
mean_field_scale = tfb.ScaleMatvecLinearOperatorBlock(block_diag_linop)
mean_field_loc = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
mean_field_surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
mean_field_loc, # allow for nonzero mean
mean_field_scale # apply the block matrix transformation to the standard Normal distribution
]))
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
mean_field_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
mean_field_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mean_field_samples = mean_field_surrogate_posterior.sample(1000)
mean_field_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mean_field_samples)
- mean_field_surrogate_posterior.log_prob(mean_field_samples))
print('Mean-field surrogate posterior ELBO: {}'.format(mean_field_final_elbo))
plt.plot(mean_field_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Mean-field surrogate posterior ELBO: -1065.7652587890625
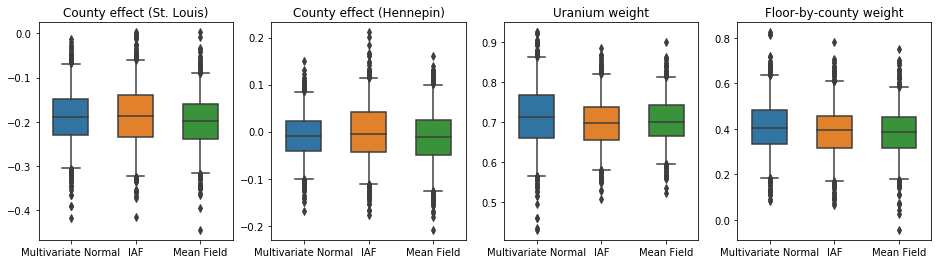
Dans ce cas, le champ moyen a posteriori de substitution donne des résultats similaires aux postérieurs de substitution plus expressifs, indiquant que ce modèle plus simple peut être adéquat pour la tâche d'inférence.
results['Mean Field'] = pack_samples(mean_field_samples)
plot_boxplot(results)
Vérité terrain : l'hamiltonien Monte Carlo (HMC)
Nous utilisons HMC pour générer des échantillons de « vérité terrain » à partir du vrai postérieur, pour comparaison avec les résultats des postérieurs de substitution.
num_chains = 8
num_leapfrog_steps = 3
step_size = 0.4
num_steps=20000
flat_event_shape = tf.nest.flatten(target_model.event_shape)
enum_components = list(range(len(flat_event_shape)))
bijector = tfb.Restructure(
enum_components,
tf.nest.pack_sequence_as(target_model.event_shape, enum_components))(
target_model.experimental_default_event_space_bijector())
current_state = bijector(
tf.nest.map_structure(
lambda e: tf.zeros([num_chains] + list(e), dtype=tf.float32),
target_model.event_shape))
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_model.unnormalized_log_prob,
num_leapfrog_steps=num_leapfrog_steps,
step_size=[tf.fill(s.shape, step_size) for s in current_state])
hmc = tfp.mcmc.TransformedTransitionKernel(
hmc, bijector)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(num_steps // 2 * 0.8),
target_accept_prob=0.9)
chain, is_accepted = tf.function(
lambda current_state: tfp.mcmc.sample_chain(
current_state=current_state,
kernel=hmc,
num_results=num_steps // 2,
num_burnin_steps=num_steps // 2,
trace_fn=lambda _, pkr:
(pkr.inner_results.inner_results.is_accepted),
),
autograph=False,
jit_compile=True)(current_state)
accept_rate = tf.reduce_mean(tf.cast(is_accepted, tf.float32))
ess = tf.nest.map_structure(
lambda c: tfp.mcmc.effective_sample_size(
c,
cross_chain_dims=1,
filter_beyond_positive_pairs=True),
chain)
r_hat = tf.nest.map_structure(tfp.mcmc.potential_scale_reduction, chain)
hmc_samples = pack_samples(
tf.nest.pack_sequence_as(target_model.event_shape, chain))
print('Acceptance rate is {}'.format(accept_rate))
Acceptance rate is 0.9008625149726868
Tracez des traces d'échantillons pour vérifier l'intégrité des résultats de la console HMC.
def plot_traces(var_name, samples):
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
s = samples.numpy()[:, chain]
axes[0].plot(s, alpha=0.7)
sns.kdeplot(s, ax=axes[1], shade=False)
axes[0].title.set_text("'{}' trace".format(var_name))
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
warnings.filterwarnings('ignore')
for var, var_samples in hmc_samples.items():
plot_traces(var, var_samples)




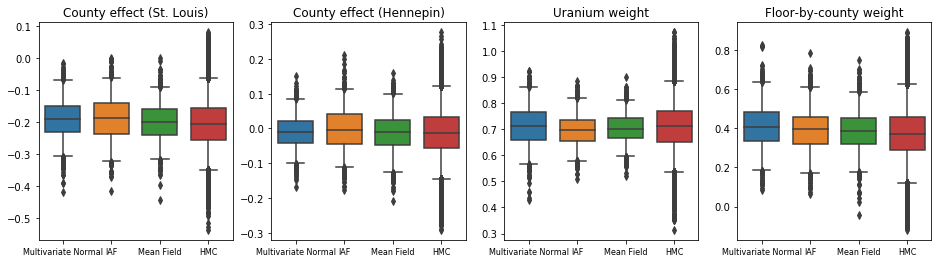
Les trois paramètres postérieurs de substitution ont produit des intervalles crédibles qui sont visuellement similaires aux échantillons HMC, bien que parfois sous-dispersés en raison de l'effet de la perte ELBO, comme cela est courant dans VI.
results['HMC'] = hmc_samples
plot_boxplot(results)
Résultats supplémentaires
Fonctions de traçage
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'medium'})
def plot_loss_and_elbo():
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].scatter([0, 1, 2],
[mvn_final_elbo.numpy(),
iaf_final_elbo.numpy(),
mean_field_final_elbo.numpy()])
axes[0].set_xticks(ticks=[0, 1, 2])
axes[0].set_xticklabels(labels=[
'Multivariate Normal', 'IAF', 'Mean Field'])
axes[0].title.set_text('Evidence Lower Bound (ELBO)')
axes[1].plot(mvn_loss, label='Multivariate Normal')
axes[1].plot(iaf_loss, label='IAF')
axes[1].plot(mean_field_loss, label='Mean Field')
axes[1].set_ylim([1000, 4000])
axes[1].set_xlabel('Training step')
axes[1].set_ylabel('Loss (negative ELBO)')
axes[1].title.set_text('Loss')
plt.legend()
plt.show()
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'small'})
def plot_kdes(num_chains=8):
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
k = list(results.values())[0].keys()
plot_results = {
v: {p: results[p][v] for p in results} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
ax = axes[i % 2, i // 2]
for posterior, posterior_results in var_results.items():
if posterior == 'HMC':
label = posterior
for chain in range(num_chains):
sns.kdeplot(
posterior_results[:, chain],
ax=ax, shade=False, color='k', linestyle=':', label=label)
label=None
else:
sns.kdeplot(
posterior_results, ax=ax, shade=False, label=posterior)
ax.title.set_text('{}'.format(var))
ax.legend()
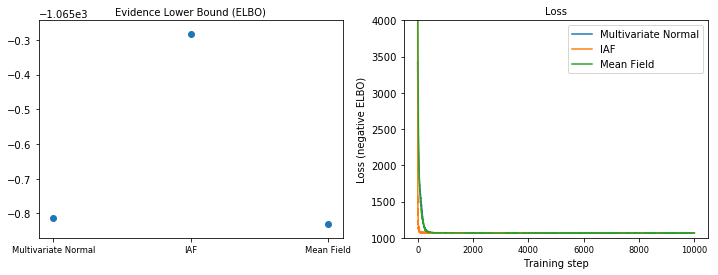
Limite inférieure des preuves (ELBO)
L'IAF, de loin le substitut postérieur le plus grand et le plus flexible, converge vers la limite inférieure de preuve la plus élevée (ELBO).
plot_loss_and_elbo()
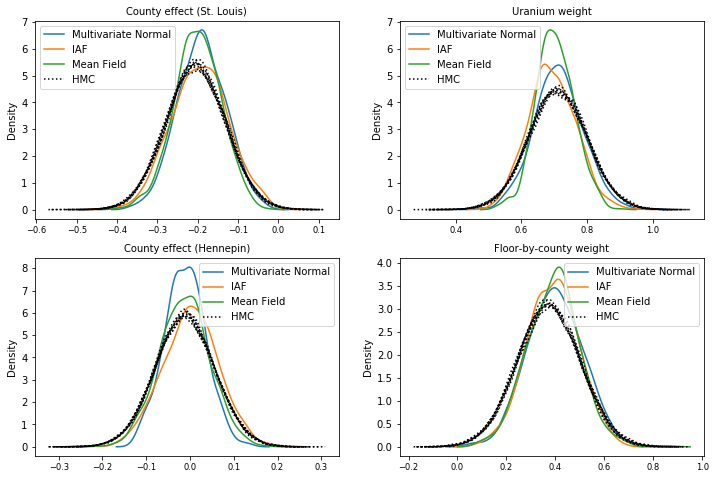
Échantillons postérieurs
Échantillons de chaque a posteriori de substitution, comparés aux échantillons de vérité terrain HMC (une visualisation différente des échantillons montrés dans les boîtes à moustaches).
plot_kdes()
Conclusion
Dans ce Colab, nous avons construit des VI postérieurs de substitution à l'aide de distributions conjointes et de bijecteurs en plusieurs parties, et les avons ajustés pour estimer des intervalles crédibles pour les poids dans un modèle de régression sur l'ensemble de données sur le radon. Pour ce modèle simple, des postérieurs de substitution plus expressifs ont fonctionné de la même manière qu'un postérieur de substitution à champ moyen. Les outils que nous avons démontrés, cependant, peuvent être utilisés pour construire une large gamme de postérieurs de substitution flexibles adaptés à des modèles plus complexes.
