 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
S'appuyant sur des comparaisons faites dans le MNIST tutoriel, ce tutoriel explore les travaux récents de Huang et al. qui montre comment différents ensembles de données affectent les comparaisons de performances. Dans le travail, les auteurs cherchent à comprendre comment et quand les modèles d'apprentissage automatique classiques peuvent apprendre aussi bien (ou mieux que) les modèles quantiques. Le travail présente également une séparation empirique des performances entre le modèle d'apprentissage automatique classique et quantique via un ensemble de données soigneusement conçu. Vous serez:
- Préparez un jeu de données Fashion-MNIST de dimension réduite.
- Utilisez des circuits quantiques pour ré-étiqueter l'ensemble de données et calculer les caractéristiques du noyau quantique projeté (PQK).
- Entraînez un réseau de neurones classique sur l'ensemble de données ré-étiqueté et comparez les performances avec un modèle qui a accès aux fonctionnalités PQK.
Installer
pip install tensorflow==2.4.1 tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
1. Préparation des données
Vous commencerez par préparer l'ensemble de données fashion-MNIST pour une exécution sur un ordinateur quantique.
1.1 Télécharger fashion-MNIST
La première étape consiste à obtenir l'ensemble de données fashion-mnist traditionnel. Cela peut être fait à l' aide du tf.keras.datasets module.
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train/255.0, x_test/255.0
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
Number of original training examples: 60000 Number of original test examples: 10000
Filtrez l'ensemble de données pour ne conserver que les t-shirts/tops et robes, supprimez les autres classes. En même temps , convertir l'étiquette, y , à booléenne: true pour 0 et False pour 3.
def filter_03(x, y):
keep = (y == 0) | (y == 3)
x, y = x[keep], y[keep]
y = y == 0
return x,y
x_train, y_train = filter_03(x_train, y_train)
x_test, y_test = filter_03(x_test, y_test)
print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))
Number of filtered training examples: 12000 Number of filtered test examples: 2000
print(y_train[0])
plt.imshow(x_train[0, :, :])
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7f6db42c3460>

1.2 Réduire l'échelle des images
Tout comme dans l'exemple du MNIST, vous devrez réduire l'échelle de ces images afin de respecter les limites des ordinateurs quantiques actuels. Cependant , cette fois , vous utiliserez une transformation de PCA pour réduire les dimensions au lieu d'une tf.image.resize opération.
def truncate_x(x_train, x_test, n_components=10):
"""Perform PCA on image dataset keeping the top `n_components` components."""
n_points_train = tf.gather(tf.shape(x_train), 0)
n_points_test = tf.gather(tf.shape(x_test), 0)
# Flatten to 1D
x_train = tf.reshape(x_train, [n_points_train, -1])
x_test = tf.reshape(x_test, [n_points_test, -1])
# Normalize.
feature_mean = tf.reduce_mean(x_train, axis=0)
x_train_normalized = x_train - feature_mean
x_test_normalized = x_test - feature_mean
# Truncate.
e_values, e_vectors = tf.linalg.eigh(
tf.einsum('ji,jk->ik', x_train_normalized, x_train_normalized))
return tf.einsum('ij,jk->ik', x_train_normalized, e_vectors[:,-n_components:]), \
tf.einsum('ij,jk->ik', x_test_normalized, e_vectors[:, -n_components:])
DATASET_DIM = 10
x_train, x_test = truncate_x(x_train, x_test, n_components=DATASET_DIM)
print(f'New datapoint dimension:', len(x_train[0]))
New datapoint dimension: 10
La dernière étape consiste à réduire la taille de l'ensemble de données à seulement 1 000 points de données d'entraînement et 200 points de données de test.
N_TRAIN = 1000
N_TEST = 200
x_train, x_test = x_train[:N_TRAIN], x_test[:N_TEST]
y_train, y_test = y_train[:N_TRAIN], y_test[:N_TEST]
print("New number of training examples:", len(x_train))
print("New number of test examples:", len(x_test))
New number of training examples: 1000 New number of test examples: 200
2. Réétiquetage et calcul des fonctionnalités PQK
Vous allez maintenant préparer un ensemble de données quantiques "sur pilotis" en incorporant des composants quantiques et en ré-étiquetant l'ensemble de données tronqué fashion-MNIST que vous avez créé ci-dessus. Afin d'obtenir la plus grande séparation entre les méthodes quantiques et classiques, vous allez d'abord préparer les fonctionnalités PQK, puis réétiqueter les sorties en fonction de leurs valeurs.
2.1 Encodage quantique et fonctionnalités PQK
Vous allez créer un nouvel ensemble de fonctionnalités, basé sur x_train , y_train , x_test et y_test qui est défini comme le 1-MRD sur tous les qubits de:
\(V(x_{\text{train} } / n_{\text{trotter} }) ^ {n_{\text{trotter} } } U_{\text{1qb} } | 0 \rangle\)
Où \(U_\text{1qb}\) est un mur de rotation des qubits simples et \(V(\hat{\theta}) = e^{-i\sum_i \hat{\theta_i} (X_i X_{i+1} + Y_i Y_{i+1} + Z_i Z_{i+1})}\)
Tout d'abord, vous pouvez générer le mur des rotations d'un seul qubit :
def single_qubit_wall(qubits, rotations):
"""Prepare a single qubit X,Y,Z rotation wall on `qubits`."""
wall_circuit = cirq.Circuit()
for i, qubit in enumerate(qubits):
for j, gate in enumerate([cirq.X, cirq.Y, cirq.Z]):
wall_circuit.append(gate(qubit) ** rotations[i][j])
return wall_circuit
Vous pouvez vérifier rapidement que cela fonctionne en regardant le circuit :
SVGCircuit(single_qubit_wall(
cirq.GridQubit.rect(1,4), np.random.uniform(size=(4, 3))))
Ensuite , vous pouvez préparer \(V(\hat{\theta})\) avec l'aide de tfq.util.exponential qui peut exponentiate tout trajet cirq.PauliSum objets:
def v_theta(qubits):
"""Prepares a circuit that generates V(\theta)."""
ref_paulis = [
cirq.X(q0) * cirq.X(q1) + \
cirq.Y(q0) * cirq.Y(q1) + \
cirq.Z(q0) * cirq.Z(q1) for q0, q1 in zip(qubits, qubits[1:])
]
exp_symbols = list(sympy.symbols('ref_0:'+str(len(ref_paulis))))
return tfq.util.exponential(ref_paulis, exp_symbols), exp_symbols
Ce circuit peut être un peu plus difficile à vérifier en regardant, mais vous pouvez toujours examiner un cas à deux qubits pour voir ce qui se passe :
test_circuit, test_symbols = v_theta(cirq.GridQubit.rect(1, 2))
print(f'Symbols found in circuit:{test_symbols}')
SVGCircuit(test_circuit)
Symbols found in circuit:[ref_0]
Vous disposez maintenant de tous les éléments constitutifs dont vous avez besoin pour assembler vos circuits d'encodage complets :
def prepare_pqk_circuits(qubits, classical_source, n_trotter=10):
"""Prepare the pqk feature circuits around a dataset."""
n_qubits = len(qubits)
n_points = len(classical_source)
# Prepare random single qubit rotation wall.
random_rots = np.random.uniform(-2, 2, size=(n_qubits, 3))
initial_U = single_qubit_wall(qubits, random_rots)
# Prepare parametrized V
V_circuit, symbols = v_theta(qubits)
exp_circuit = cirq.Circuit(V_circuit for t in range(n_trotter))
# Convert to `tf.Tensor`
initial_U_tensor = tfq.convert_to_tensor([initial_U])
initial_U_splat = tf.tile(initial_U_tensor, [n_points])
full_circuits = tfq.layers.AddCircuit()(
initial_U_splat, append=exp_circuit)
# Replace placeholders in circuits with values from `classical_source`.
return tfq.resolve_parameters(
full_circuits, tf.convert_to_tensor([str(x) for x in symbols]),
tf.convert_to_tensor(classical_source*(n_qubits/3)/n_trotter))
Choisissez quelques qubits et préparez les circuits d'encodage des données :
qubits = cirq.GridQubit.rect(1, DATASET_DIM + 1)
q_x_train_circuits = prepare_pqk_circuits(qubits, x_train)
q_x_test_circuits = prepare_pqk_circuits(qubits, x_test)
Ensuite, calculer les caractéristiques PQK basé sur le 1-RDM des circuits d'ensembles de données ci - dessus et stocker les résultats dans rdm , un tf.Tensor avec la forme [n_points, n_qubits, 3] . Les entrées de rdm[i][j][k] = \(\langle \psi_i | OP^k_j | \psi_i \rangle\) où i indexe plus de points de données, j index sur qubits et k index sur \(\lbrace \hat{X}, \hat{Y}, \hat{Z} \rbrace\) .
def get_pqk_features(qubits, data_batch):
"""Get PQK features based on above construction."""
ops = [[cirq.X(q), cirq.Y(q), cirq.Z(q)] for q in qubits]
ops_tensor = tf.expand_dims(tf.reshape(tfq.convert_to_tensor(ops), -1), 0)
batch_dim = tf.gather(tf.shape(data_batch), 0)
ops_splat = tf.tile(ops_tensor, [batch_dim, 1])
exp_vals = tfq.layers.Expectation()(data_batch, operators=ops_splat)
rdm = tf.reshape(exp_vals, [batch_dim, len(qubits), -1])
return rdm
x_train_pqk = get_pqk_features(qubits, q_x_train_circuits)
x_test_pqk = get_pqk_features(qubits, q_x_test_circuits)
print('New PQK training dataset has shape:', x_train_pqk.shape)
print('New PQK testing dataset has shape:', x_test_pqk.shape)
New PQK training dataset has shape: (1000, 11, 3) New PQK testing dataset has shape: (200, 11, 3)
2.2 Ré-étiquetage basé sur les fonctionnalités PQK
Maintenant que vous avez ces caractéristiques quantiques généré en x_train_pqk et x_test_pqk , il est temps de réétiqueter l'ensemble de données. Pour atteindre un maximum entre seperation quantique et de la performance classique , vous pouvez ré-étiqueter l'ensemble de données sur la base des informations de spectre trouvées dans x_train_pqk et x_test_pqk .
def compute_kernel_matrix(vecs, gamma):
"""Computes d[i][j] = e^ -gamma * (vecs[i] - vecs[j]) ** 2 """
scaled_gamma = gamma / (
tf.cast(tf.gather(tf.shape(vecs), 1), tf.float32) * tf.math.reduce_std(vecs))
return scaled_gamma * tf.einsum('ijk->ij',(vecs[:,None,:] - vecs) ** 2)
def get_spectrum(datapoints, gamma=1.0):
"""Compute the eigenvalues and eigenvectors of the kernel of datapoints."""
KC_qs = compute_kernel_matrix(datapoints, gamma)
S, V = tf.linalg.eigh(KC_qs)
S = tf.math.abs(S)
return S, V
S_pqk, V_pqk = get_spectrum(
tf.reshape(tf.concat([x_train_pqk, x_test_pqk], 0), [-1, len(qubits) * 3]))
S_original, V_original = get_spectrum(
tf.cast(tf.concat([x_train, x_test], 0), tf.float32), gamma=0.005)
print('Eigenvectors of pqk kernel matrix:', V_pqk)
print('Eigenvectors of original kernel matrix:', V_original)
Eigenvectors of pqk kernel matrix: tf.Tensor( [[-2.09569391e-02 1.05973557e-02 2.16634180e-02 ... 2.80352887e-02 1.55521873e-02 2.82677952e-02] [-2.29303762e-02 4.66355234e-02 7.91163836e-03 ... -6.14174758e-04 -7.07804322e-01 2.85902526e-02] [-1.77853629e-02 -3.00758495e-03 -2.55225878e-02 ... -2.40783971e-02 2.11018627e-03 2.69009806e-02] ... [ 6.05797209e-02 1.32483775e-02 2.69536003e-02 ... -1.38843581e-02 3.05043962e-02 3.85345481e-02] [ 6.33309558e-02 -3.04112374e-03 9.77444276e-03 ... 7.48321265e-02 3.42793856e-03 3.67484428e-02] [ 5.86028099e-02 5.84433973e-03 2.64811981e-03 ... 2.82612257e-02 -3.80136147e-02 3.29943895e-02]], shape=(1200, 1200), dtype=float32) Eigenvectors of original kernel matrix: tf.Tensor( [[ 0.03835681 0.0283473 -0.01169789 ... 0.02343717 0.0211248 0.03206972] [-0.04018159 0.00888097 -0.01388255 ... 0.00582427 0.717551 0.02881948] [-0.0166719 0.01350376 -0.03663862 ... 0.02467175 -0.00415936 0.02195409] ... [-0.03015648 -0.01671632 -0.01603392 ... 0.00100583 -0.00261221 0.02365689] [ 0.0039777 -0.04998879 -0.00528336 ... 0.01560401 -0.04330755 0.02782002] [-0.01665728 -0.00818616 -0.0432341 ... 0.00088256 0.00927396 0.01875088]], shape=(1200, 1200), dtype=float32)
Vous avez maintenant tout ce dont vous avez besoin pour ré-étiqueter l'ensemble de données ! Vous pouvez désormais consulter l'organigramme pour mieux comprendre comment maximiser la séparation des performances lors du réétiquetage de l'ensemble de données :
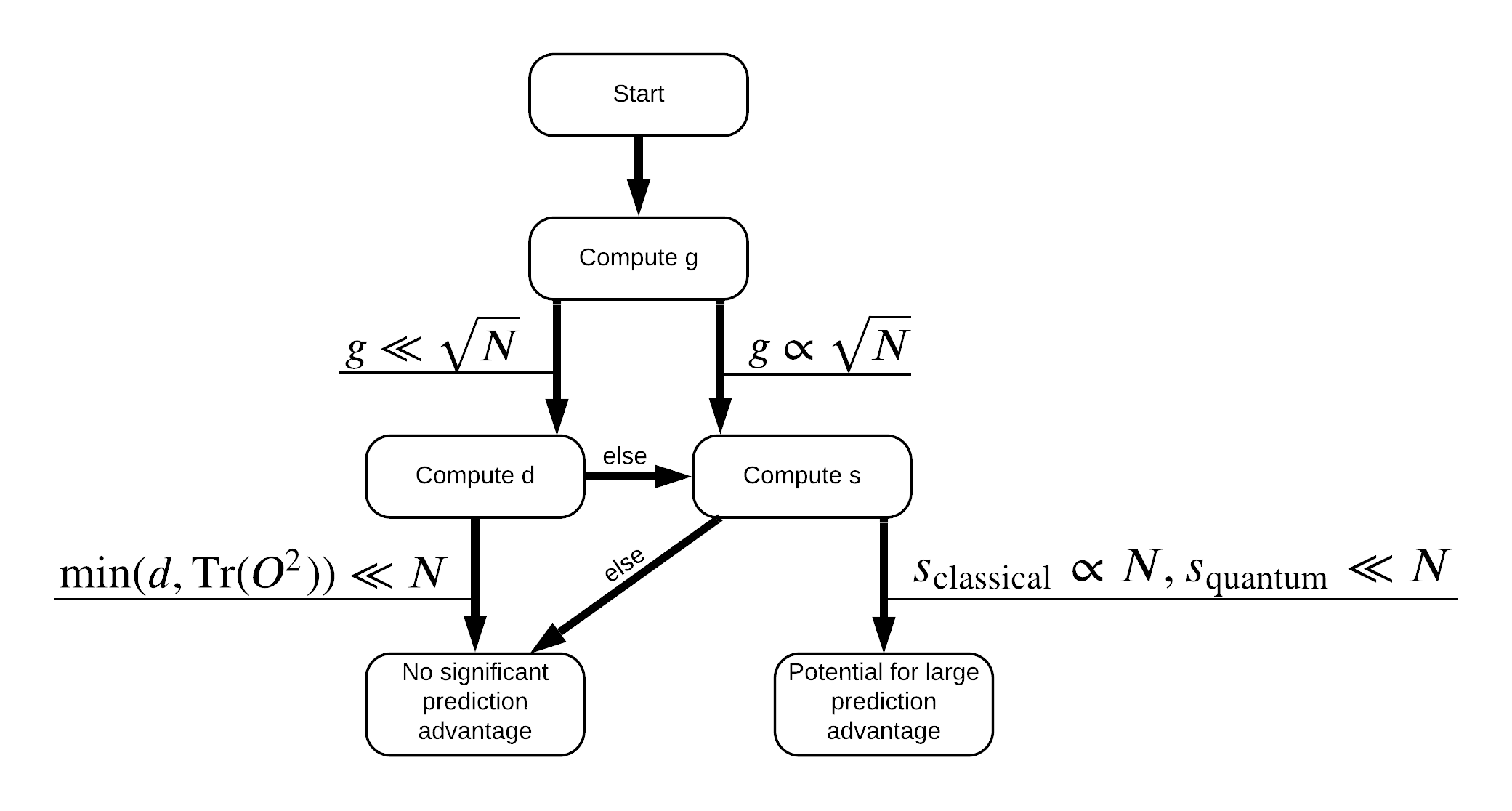
Afin de maximiser la séparation entre quantique et les modèles classiques, vous essayez de maximiser la différence géométrique entre l'ensemble de données d' origine et les caractéristiques PQK matrices noyau \(g(K_1 || K_2) = \sqrt{ || \sqrt{K_2} K_1^{-1} \sqrt{K_2} || _\infty}\) en utilisant S_pqk, V_pqk et S_original, V_original . Une valeur de \(g\) assure que vous déplacer d' abord vers la droite dans le bas d'organigramme vers un avantage de prédiction dans le cas quantique.
def get_stilted_dataset(S, V, S_2, V_2, lambdav=1.1):
"""Prepare new labels that maximize geometric distance between kernels."""
S_diag = tf.linalg.diag(S ** 0.5)
S_2_diag = tf.linalg.diag(S_2 / (S_2 + lambdav) ** 2)
scaling = S_diag @ tf.transpose(V) @ \
V_2 @ S_2_diag @ tf.transpose(V_2) @ \
V @ S_diag
# Generate new lables using the largest eigenvector.
_, vecs = tf.linalg.eig(scaling)
new_labels = tf.math.real(
tf.einsum('ij,j->i', tf.cast(V @ S_diag, tf.complex64), vecs[-1])).numpy()
# Create new labels and add some small amount of noise.
final_y = new_labels > np.median(new_labels)
noisy_y = (final_y ^ (np.random.uniform(size=final_y.shape) > 0.95))
return noisy_y
y_relabel = get_stilted_dataset(S_pqk, V_pqk, S_original, V_original)
y_train_new, y_test_new = y_relabel[:N_TRAIN], y_relabel[N_TRAIN:]
3. Comparer les modèles
Maintenant que vous avez préparé votre jeu de données, il est temps de comparer les performances du modèle. Vous allez créer deux petits réseaux de neurones anticipatifs et comparer les performances lorsqu'on leur donne accès aux PQK fonctionnalités de x_train_pqk .
3.1 Créer un modèle amélioré PQK
L' utilisation standards tf.keras fonctionnalités bibliothèque , vous pouvez maintenant créer et un train un modèle sur la x_train_pqk et y_train_new datapoints:
#docs_infra: no_execute
def create_pqk_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[len(qubits) * 3,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
pqk_model = create_pqk_model()
pqk_model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.003),
metrics=['accuracy'])
pqk_model.summary()
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 32) 1088 _________________________________________________________________ dense_1 (Dense) (None, 16) 528 _________________________________________________________________ dense_2 (Dense) (None, 1) 17 ================================================================= Total params: 1,633 Trainable params: 1,633 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
pqk_history = pqk_model.fit(tf.reshape(x_train_pqk, [N_TRAIN, -1]),
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(tf.reshape(x_test_pqk, [N_TEST, -1]), y_test_new))
3.2 Créer un modèle classique
Semblable au code ci-dessus, vous pouvez désormais également créer un modèle classique qui n'a pas accès aux fonctionnalités PQK dans votre jeu de données sur pilotis. Ce modèle peut être formé en utilisant x_train et y_label_new .
#docs_infra: no_execute
def create_fair_classical_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[DATASET_DIM,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.03),
metrics=['accuracy'])
model.summary()
Model: "sequential_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_3 (Dense) (None, 32) 352 _________________________________________________________________ dense_4 (Dense) (None, 16) 528 _________________________________________________________________ dense_5 (Dense) (None, 1) 17 ================================================================= Total params: 897 Trainable params: 897 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
classical_history = model.fit(x_train,
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(x_test, y_test_new))
3.3 Comparer les performances
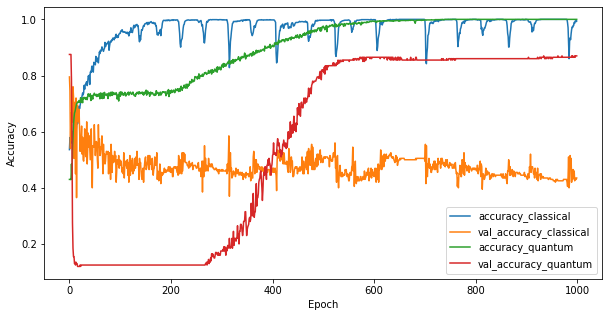
Maintenant que vous avez entraîné les deux modèles, vous pouvez rapidement tracer les écarts de performances dans les données de validation entre les deux. En règle générale, les deux modèles atteindront une précision > 0,9 sur les données d'entraînement. Cependant, sur les données de validation, il devient clair que seules les informations trouvées dans les fonctionnalités PQK sont suffisantes pour que le modèle se généralise bien aux instances invisibles.
#docs_infra: no_execute
plt.figure(figsize=(10,5))
plt.plot(classical_history.history['accuracy'], label='accuracy_classical')
plt.plot(classical_history.history['val_accuracy'], label='val_accuracy_classical')
plt.plot(pqk_history.history['accuracy'], label='accuracy_quantum')
plt.plot(pqk_history.history['val_accuracy'], label='val_accuracy_quantum')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x7f6d846ecee0>
4. Conclusions importantes
Il y a plusieurs conclusions importantes que vous pouvez tirer de cela et les MNIST expériences:
Il est très peu probable que les modèles quantiques d'aujourd'hui battent les performances des modèles classiques sur des données classiques. Surtout sur les ensembles de données classiques d'aujourd'hui qui peuvent avoir plus d'un million de points de données.
Le fait que les données puissent provenir d'un circuit quantique difficile à simuler de manière classique ne rend pas nécessairement les données difficiles à apprendre pour un modèle classique.
Des ensembles de données (en fin de compte quantiques par nature) qui sont faciles à apprendre pour les modèles quantiques et difficiles à apprendre pour les modèles classiques existent, indépendamment de l'architecture du modèle ou des algorithmes d'entraînement utilisés.
