 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Le guide Introduction aux gradients et à la différenciation automatique comprend tout ce qui est nécessaire pour calculer les gradients dans TensorFlow. Ce guide se concentre sur les fonctionnalités plus profondes et moins courantes de l'API tf.GradientTape .
Installer
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
Contrôle de l'enregistrement du gradient
Dans le guide de différenciation automatique, vous avez vu comment contrôler les variables et les tenseurs surveillés par la bande lors de la construction du calcul du gradient.
La bande a également des méthodes pour manipuler l'enregistrement.
Arrête d'enregistrer
Si vous souhaitez arrêter l'enregistrement des dégradés, vous pouvez utiliser tf.GradientTape.stop_recording pour suspendre temporairement l'enregistrement.
Cela peut être utile pour réduire les frais généraux si vous ne souhaitez pas différencier une opération compliquée au milieu de votre modèle. Cela peut inclure le calcul d'une métrique ou d'un résultat intermédiaire :
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Réinitialiser/démarrer l'enregistrement à partir de zéro
Si vous souhaitez recommencer entièrement, utilisez tf.GradientTape.reset . Le simple fait de quitter le bloc de bande dégradée et de redémarrer est généralement plus facile à lire, mais vous pouvez utiliser la méthode de reset lorsque la sortie du bloc de bande est difficile ou impossible.
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all the tape recorded so far.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Arrêtez le flux de gradient avec précision
Contrairement aux commandes de bande globales ci-dessus, la fonction tf.stop_gradient est beaucoup plus précise. Il peut être utilisé pour empêcher les dégradés de s'écouler le long d'un chemin particulier, sans avoir besoin d'accéder à la bande elle-même :
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Dégradés personnalisés
Dans certains cas, vous souhaiterez peut-être contrôler exactement la façon dont les dégradés sont calculés plutôt que d'utiliser la valeur par défaut. Ces situations incluent :
- Il n'y a pas de gradient défini pour une nouvelle opération que vous écrivez.
- Les calculs par défaut sont numériquement instables.
- Vous souhaitez mettre en cache un calcul coûteux de la passe avant.
- Vous souhaitez modifier une valeur (par exemple, en utilisant
tf.clip_by_valueoutf.math.round) sans modifier le dégradé.
Pour le premier cas, pour écrire une nouvelle opération, vous pouvez utiliser tf.RegisterGradient pour configurer la vôtre (reportez-vous à la documentation de l'API pour plus de détails). (Notez que le registre des gradients est global, modifiez-le donc avec prudence.)
Pour les trois derniers cas, vous pouvez utiliser tf.custom_gradient .
Voici un exemple qui applique tf.clip_by_norm au dégradé intermédiaire :
# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, shape=(), dtype=float32)
Reportez-vous à la documentation de l'API de tf.custom_gradient pour plus de détails.
Dégradés personnalisés dans SavedModel
Les dégradés personnalisés peuvent être enregistrés dans SavedModel à l'aide de l'option tf.saved_model.SaveOptions(experimental_custom_gradients=True) .
Pour être enregistrée dans le SavedModel, la fonction de gradient doit être traçable (pour en savoir plus, consultez le guide Meilleures performances avec tf.function ).
class MyModule(tf.Module):
@tf.function(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
model = MyModule()
tf.saved_model.save(
model,
'saved_model',
options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
INFO:tensorflow:Assets written to: saved_model/assets tf.Tensor(2.0, shape=(), dtype=float32)
Remarque à propos de l'exemple ci-dessus : si vous essayez de remplacer le code ci-dessus par tf.saved_model.SaveOptions(experimental_custom_gradients=False) , le dégradé produira toujours le même résultat lors du chargement. La raison en est que le registre des dégradés contient toujours le dégradé personnalisé utilisé dans la fonction call_custom_op . Toutefois, si vous redémarrez le runtime après avoir enregistré sans dégradés personnalisés, l'exécution du modèle chargé sous tf.GradientTape l'erreur : LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .
Plusieurs bandes
Plusieurs bandes interagissent de manière transparente.
Par exemple, ici, chaque bande regarde un ensemble différent de tenseurs :
x0 = tf.constant(0.0)
x1 = tf.constant(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
Gradients d'ordre supérieur
Les opérations à l'intérieur du gestionnaire de contexte tf.GradientTape sont enregistrées pour une différenciation automatique. Si des gradients sont calculés dans ce contexte, le calcul du gradient est également enregistré. Par conséquent, la même API fonctionne également pour les gradients d'ordre supérieur.
Par example:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient inside the outer `t2` context manager
# which means the gradient computation is differentiable as well.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0 d2y_dx2: 6.0
Bien que cela vous donne la dérivée seconde d'une fonction scalaire , ce modèle ne se généralise pas pour produire une matrice hessienne, puisque tf.GradientTape.gradient ne calcule que le gradient d'un scalaire. Pour construire une matrice Hessienne , allez à l' exemple Hessien sous la section Jacobienne .
"Appels imbriqués à tf.GradientTape.gradient " est un bon modèle lorsque vous calculez un scalaire à partir d'un dégradé, puis le scalaire résultant agit comme une source pour un deuxième calcul de gradient, comme dans l'exemple suivant.
Exemple : régularisation du gradient d'entrée
De nombreux modèles sont susceptibles d'« exemples contradictoires ». Cet ensemble de techniques modifie l'entrée du modèle pour confondre la sortie du modèle. L'implémentation la plus simple, telle que l' exemple Adversarial utilisant l'attaque Fast Gradient Signed Method, prend une seule étape le long du gradient de la sortie par rapport à l'entrée; le "gradient d'entrée".
Une technique pour augmenter la robustesse aux exemples contradictoires est la régularisation du gradient d'entrée (Finlay & Oberman, 2019), qui tente de minimiser l'ampleur du gradient d'entrée. Si le gradient d'entrée est faible, le changement dans la sortie doit également être faible.
Vous trouverez ci-dessous une implémentation naïve de la régularisation du gradient d'entrée. La mise en œuvre est :
- Calculez le gradient de la sortie par rapport à l'entrée à l'aide d'un ruban intérieur.
- Calculez l'ampleur de ce gradient d'entrée.
- Calculez le gradient de cette grandeur par rapport au modèle.
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The inner tape only takes the gradient with respect to the input,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the input gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the input gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
Jacobiens
Tous les exemples précédents prenaient les gradients d'une cible scalaire par rapport à un ou plusieurs tenseurs sources.
La matrice jacobienne représente les gradients d'une fonction à valeur vectorielle. Chaque ligne contient le dégradé d'un des éléments du vecteur.
La méthode tf.GradientTape.jacobian permet de calculer efficacement une matrice jacobienne.
Noter que:
- Comme
gradient: L'argumentsourcespeut être un tenseur ou un conteneur de tenseurs. - Contrairement au
gradient: le tenseurtargetdoit être un tenseur unique.
Source scalaire
Comme premier exemple, voici le jacobien d'un vecteur-cible par rapport à un scalaire-source.
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
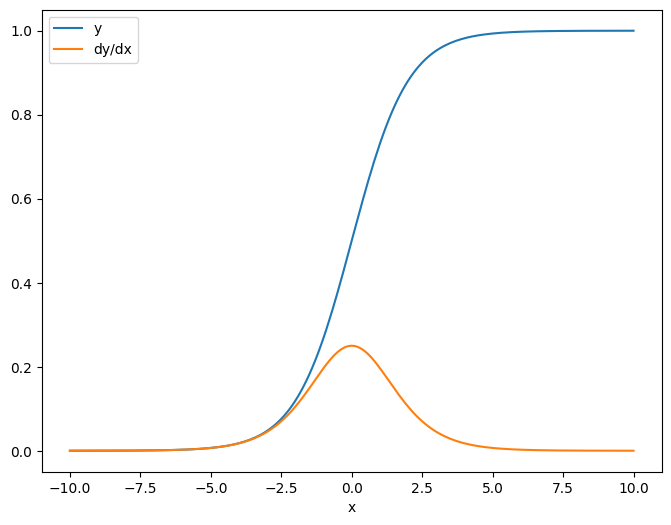
Lorsque vous prenez le jacobien par rapport à un scalaire, le résultat a la forme de la cible et donne le gradient de chaque élément par rapport à la source :
print(y.shape)
print(dy_dx.shape)
(201,) (201,)
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
Source de tenseur
Que l'entrée soit scalaire ou tenseur, tf.GradientTape.jacobian calcule efficacement le gradient de chaque élément de la source par rapport à chaque élément de la ou des cibles.
Par exemple, la sortie de ce calque a la forme (10, 7) :
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.shape
TensorShape([7, 10])
Et la forme du noyau de la couche est (5, 10) :
layer.kernel.shape
TensorShape([5, 10])
La forme du jacobien de la sortie par rapport au noyau est ces deux formes concaténées :
j = tape.jacobian(y, layer.kernel)
j.shape
TensorShape([7, 10, 5, 10])
Si vous additionnez sur les dimensions de la cible, il vous reste le gradient de la somme qui aurait été calculé par tf.GradientTape.gradient :
g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.shape: (5, 10) delta: 2.3841858e-07
Exemple : hessois
Bien que tf.GradientTape ne donne pas de méthode explicite pour construire une matrice Hessienne, il est possible d'en construire une en utilisant la méthode tf.GradientTape.jacobian .
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')
layer.kernel.shape: (5, 8) h.shape: (5, 8, 5, 8)
Pour utiliser ce Hessian pour une étape de la méthode de Newton , vous devez d'abord aplatir ses axes dans une matrice et aplatir le gradient dans un vecteur :
n_params = tf.reduce_prod(layer1.kernel.shape)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
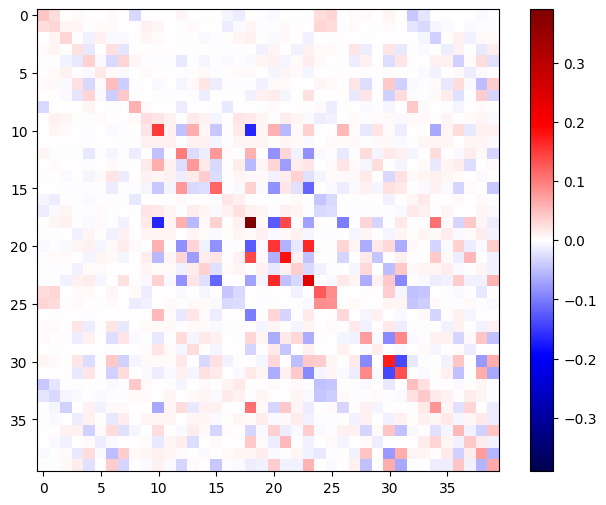
La matrice Hessienne doit être symétrique :
def imshow_zero_center(image, **kwargs):
lim = tf.reduce_max(abs(image))
plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
L'étape de mise à jour de la méthode de Newton est illustrée ci-dessous :
eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps
# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)
# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))
Bien que cela soit relativement simple pour un seul tf.Variable , l'appliquer à un modèle non trivial nécessiterait une concaténation et un découpage minutieux pour produire un hessien complet sur plusieurs variables.
Lot jacobien
Dans certains cas, vous souhaitez prendre le jacobien de chacune d'une pile de cibles par rapport à une pile de sources, où les jacobiens de chaque paire cible-source sont indépendants.
Par exemple, ici l'entrée x est mise en forme (batch, ins) et la sortie y est mise en forme (batch, outs) :
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.shape
TensorShape([7, 6])
Le jacobien complet de y par rapport à x a la forme (batch, ins, batch, outs) , même si vous ne voulez que (batch, ins, outs) :
j = tape.jacobian(y, x)
j.shape
TensorShape([7, 6, 7, 5])
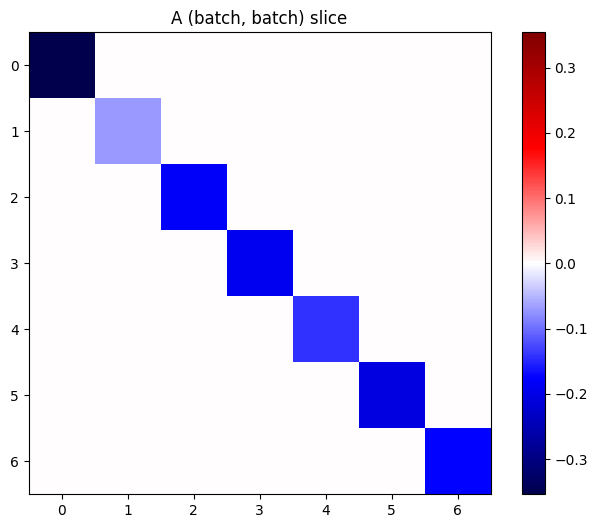
Si les gradients de chaque élément de la pile sont indépendants, alors chaque tranche (batch, batch) de ce tenseur est une matrice diagonale :
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
def plot_as_patches(j):
# Reorder axes so the diagonals will each form a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between each patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to form a single image.
s = j.shape
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
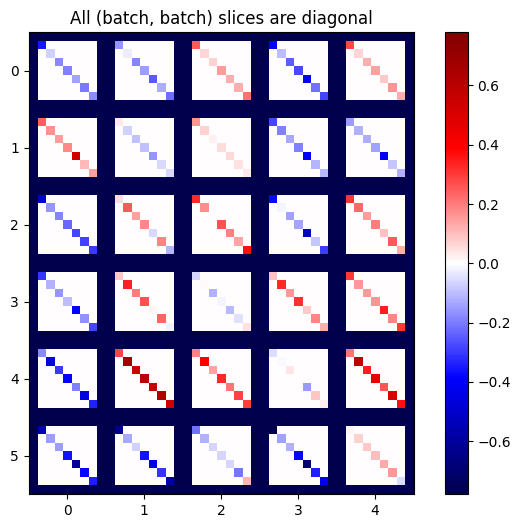
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
Pour obtenir le résultat souhaité, vous pouvez additionner la dimension du batch en double, ou bien sélectionner les diagonales à l'aide tf.einsum :
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)
(7, 6, 5) (7, 6, 5)
Il serait beaucoup plus efficace de faire le calcul sans la dimension supplémentaire en premier lieu. La méthode tf.GradientTape.batch_jacobian fait exactement cela :
jb = tape.batch_jacobian(y, x)
jb.shape
WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. TensorShape([7, 6, 5])
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, training=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')
WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. j.shape: (7, 6, 7, 5)
plot_as_patches(j)
_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")
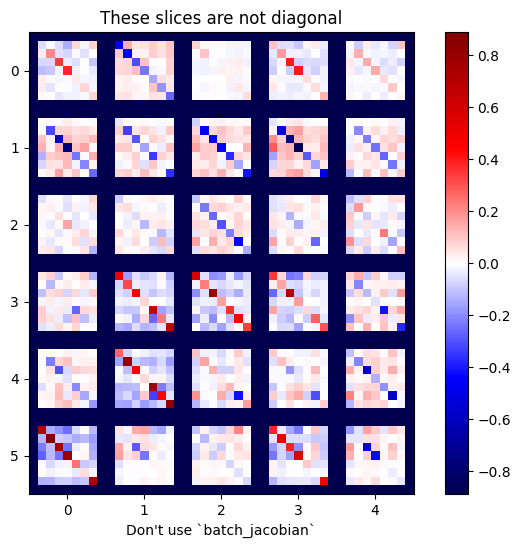
Dans ce cas, batch_jacobian s'exécute toujours et renvoie quelque chose avec la forme attendue, mais son contenu a une signification peu claire :
jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')
jb.shape: (7, 6, 5)
