 Veja no TensorFlow.org Veja no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
import tensorflow as tf
import numpy as np
Tensores são arrays multidimensionais com um tipo uniforme (chamado de dtype ). Você pode ver todos os dtypes suportados em tf.dtypes.DType .
Se você estiver familiarizado com NumPy , os tensores são (mais ou menos) como np.arrays .
Todos os tensores são imutáveis como números e strings do Python: você nunca pode atualizar o conteúdo de um tensor, apenas criar um novo.
Fundamentos
Vamos criar alguns tensores básicos.
Aqui está um tensor "escalar" ou "rank-0". Um escalar contém um único valor e nenhum "eixo".
# This will be an int32 tensor by default; see "dtypes" below.
rank_0_tensor = tf.constant(4)
print(rank_0_tensor)
tf.Tensor(4, shape=(), dtype=int32)
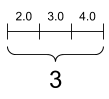
Um tensor "vetor" ou "rank-1" é como uma lista de valores. Um vetor tem um eixo:
# Let's make this a float tensor.
rank_1_tensor = tf.constant([2.0, 3.0, 4.0])
print(rank_1_tensor)
tf.Tensor([2. 3. 4.], shape=(3,), dtype=float32)
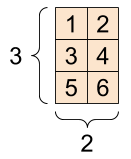
Um tensor "matriz" ou "rank-2" tem dois eixos:
# If you want to be specific, you can set the dtype (see below) at creation time
rank_2_tensor = tf.constant([[1, 2],
[3, 4],
[5, 6]], dtype=tf.float16)
print(rank_2_tensor)
tf.Tensor( [[1. 2.] [3. 4.] [5. 6.]], shape=(3, 2), dtype=float16)
Um escalar, forma: [] | Um vetor, forma: [3] | Uma matriz, forma: [3, 2] |
|---|---|---|
 |  |  |
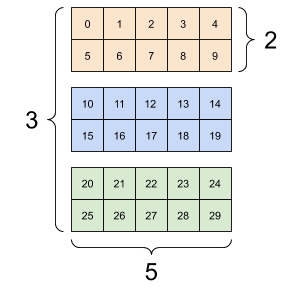
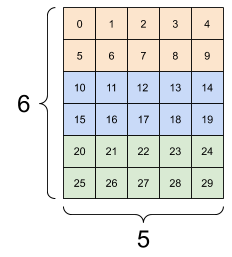
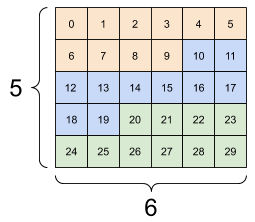
Os tensores podem ter mais eixos; aqui está um tensor com três eixos:
# There can be an arbitrary number of
# axes (sometimes called "dimensions")
rank_3_tensor = tf.constant([
[[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]],
[[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]],
[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29]],])
print(rank_3_tensor)
tf.Tensor( [[[ 0 1 2 3 4] [ 5 6 7 8 9]] [[10 11 12 13 14] [15 16 17 18 19]] [[20 21 22 23 24] [25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)
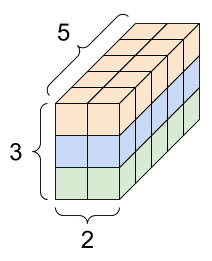
Há muitas maneiras de visualizar um tensor com mais de dois eixos.
Um tensor de 3 eixos, forma: [3, 2, 5] | ||
|---|---|---|
 |  |  |
Você pode converter um tensor em um array NumPy usando np.array ou o método tensor.numpy :
np.array(rank_2_tensor)
array([[1., 2.],
[3., 4.],
[5., 6.]], dtype=float16)
rank_2_tensor.numpy()
array([[1., 2.],
[3., 4.],
[5., 6.]], dtype=float16)
Tensores geralmente contêm floats e ints, mas têm muitos outros tipos, incluindo:
- números complexos
- cordas
A classe base tf.Tensor requer que os tensores sejam "retangulares" --- isto é, ao longo de cada eixo, cada elemento é do mesmo tamanho. No entanto, existem tipos especializados de tensores que podem lidar com diferentes formas:
- Tensores irregulares (veja RaggedTensor abaixo)
- Tensores esparsos (veja SparseTensor abaixo)
Você pode fazer matemática básica em tensores, incluindo adição, multiplicação por elementos e multiplicação de matrizes.
a = tf.constant([[1, 2],
[3, 4]])
b = tf.constant([[1, 1],
[1, 1]]) # Could have also said `tf.ones([2,2])`
print(tf.add(a, b), "\n")
print(tf.multiply(a, b), "\n")
print(tf.matmul(a, b), "\n")
tf.Tensor( [[2 3] [4 5]], shape=(2, 2), dtype=int32) tf.Tensor( [[1 2] [3 4]], shape=(2, 2), dtype=int32) tf.Tensor( [[3 3] [7 7]], shape=(2, 2), dtype=int32)
print(a + b, "\n") # element-wise addition
print(a * b, "\n") # element-wise multiplication
print(a @ b, "\n") # matrix multiplication
tf.Tensor( [[2 3] [4 5]], shape=(2, 2), dtype=int32) tf.Tensor( [[1 2] [3 4]], shape=(2, 2), dtype=int32) tf.Tensor( [[3 3] [7 7]], shape=(2, 2), dtype=int32)
Tensores são usados em todos os tipos de operações (ops).
c = tf.constant([[4.0, 5.0], [10.0, 1.0]])
# Find the largest value
print(tf.reduce_max(c))
# Find the index of the largest value
print(tf.argmax(c))
# Compute the softmax
print(tf.nn.softmax(c))
tf.Tensor(10.0, shape=(), dtype=float32) tf.Tensor([1 0], shape=(2,), dtype=int64) tf.Tensor( [[2.6894143e-01 7.3105854e-01] [9.9987662e-01 1.2339458e-04]], shape=(2, 2), dtype=float32)
Sobre formas
Os tensores têm formas. Algum vocabulário:
- Forma : O comprimento (número de elementos) de cada um dos eixos de um tensor.
- Rank : Número de eixos tensores. Um escalar tem posto 0, um vetor tem posto 1, uma matriz é posto 2.
- Eixo ou Dimensão : Uma dimensão particular de um tensor.
- Tamanho : O número total de itens no tensor, o vetor de forma do produto.
Os objetos Tensors e tf.TensorShape têm propriedades convenientes para acessá-los:
rank_4_tensor = tf.zeros([3, 2, 4, 5])
Um tensor de nível 4, forma: [3, 2, 4, 5] | |
|---|---|
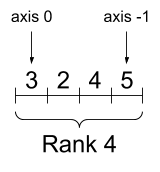 | 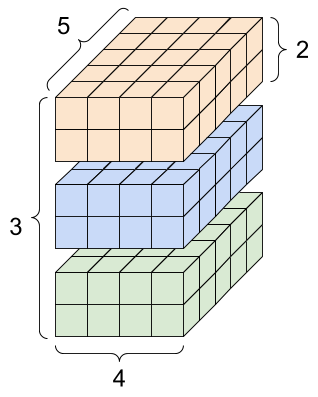 |
print("Type of every element:", rank_4_tensor.dtype)
print("Number of axes:", rank_4_tensor.ndim)
print("Shape of tensor:", rank_4_tensor.shape)
print("Elements along axis 0 of tensor:", rank_4_tensor.shape[0])
print("Elements along the last axis of tensor:", rank_4_tensor.shape[-1])
print("Total number of elements (3*2*4*5): ", tf.size(rank_4_tensor).numpy())
Type of every element: <dtype: 'float32'> Number of axes: 4 Shape of tensor: (3, 2, 4, 5) Elements along axis 0 of tensor: 3 Elements along the last axis of tensor: 5 Total number of elements (3*2*4*5): 120
Embora os eixos sejam frequentemente referidos por seus índices, você deve sempre acompanhar o significado de cada um. Freqüentemente, os eixos são ordenados de global para local: o eixo do lote primeiro, seguido pelas dimensões espaciais e os recursos para cada local por último. Dessa forma, os vetores de recursos são regiões contíguas da memória.
| Ordem típica do eixo |
|---|
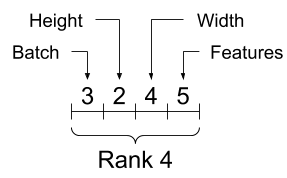 |
Indexação
Indexação de eixo único
O TensorFlow segue as regras de indexação padrão do Python, semelhantes à indexação de uma lista ou string no Python e as regras básicas para a indexação do NumPy.
- índices começam em
0 - índices negativos contam para trás a partir do final
- dois pontos,
:, são usados para fatias:start:stop:step
rank_1_tensor = tf.constant([0, 1, 1, 2, 3, 5, 8, 13, 21, 34])
print(rank_1_tensor.numpy())
[ 0 1 1 2 3 5 8 13 21 34]
A indexação com um escalar remove o eixo:
print("First:", rank_1_tensor[0].numpy())
print("Second:", rank_1_tensor[1].numpy())
print("Last:", rank_1_tensor[-1].numpy())
First: 0 Second: 1 Last: 34
A indexação com um : slice mantém o eixo:
print("Everything:", rank_1_tensor[:].numpy())
print("Before 4:", rank_1_tensor[:4].numpy())
print("From 4 to the end:", rank_1_tensor[4:].numpy())
print("From 2, before 7:", rank_1_tensor[2:7].numpy())
print("Every other item:", rank_1_tensor[::2].numpy())
print("Reversed:", rank_1_tensor[::-1].numpy())
Everything: [ 0 1 1 2 3 5 8 13 21 34] Before 4: [0 1 1 2] From 4 to the end: [ 3 5 8 13 21 34] From 2, before 7: [1 2 3 5 8] Every other item: [ 0 1 3 8 21] Reversed: [34 21 13 8 5 3 2 1 1 0]
Indexação de vários eixos
Os tensores de classificação mais alta são indexados passando vários índices.
As mesmas regras exatas que no caso de eixo único se aplicam a cada eixo independentemente.
print(rank_2_tensor.numpy())
[[1. 2.] [3. 4.] [5. 6.]]
Passando um inteiro para cada índice, o resultado é um escalar.
# Pull out a single value from a 2-rank tensor
print(rank_2_tensor[1, 1].numpy())
4.0
Você pode indexar usando qualquer combinação de inteiros e fatias:
# Get row and column tensors
print("Second row:", rank_2_tensor[1, :].numpy())
print("Second column:", rank_2_tensor[:, 1].numpy())
print("Last row:", rank_2_tensor[-1, :].numpy())
print("First item in last column:", rank_2_tensor[0, -1].numpy())
print("Skip the first row:")
print(rank_2_tensor[1:, :].numpy(), "\n")
Second row: [3. 4.] Second column: [2. 4. 6.] Last row: [5. 6.] First item in last column: 2.0 Skip the first row: [[3. 4.] [5. 6.]]
Aqui está um exemplo com um tensor de 3 eixos:
print(rank_3_tensor[:, :, 4])
tf.Tensor( [[ 4 9] [14 19] [24 29]], shape=(3, 2), dtype=int32)
| Selecionando o último recurso em todos os locais em cada exemplo no lote | |
|---|---|
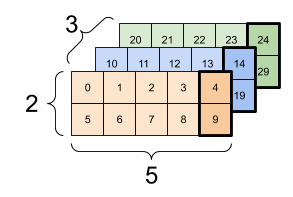 | 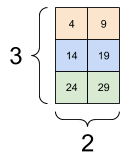 |
Leia o guia de fatiamento de tensor para saber como aplicar indexação para manipular elementos individuais em seus tensores.
Manipulando Formas
Remodelar um tensor é de grande utilidade.
# Shape returns a `TensorShape` object that shows the size along each axis
x = tf.constant([[1], [2], [3]])
print(x.shape)
(3, 1)
# You can convert this object into a Python list, too
print(x.shape.as_list())
[3, 1]
Você pode remodelar um tensor em uma nova forma. A operação tf.reshape é rápida e barata, pois os dados subjacentes não precisam ser duplicados.
# You can reshape a tensor to a new shape.
# Note that you're passing in a list
reshaped = tf.reshape(x, [1, 3])
print(x.shape)
print(reshaped.shape)
(3, 1) (1, 3)
Os dados mantêm seu layout na memória e um novo tensor é criado, com a forma solicitada, apontando para os mesmos dados. O TensorFlow usa a ordenação de memória "linha principal" no estilo C, em que o incremento do índice mais à direita corresponde a uma única etapa na memória.
print(rank_3_tensor)
tf.Tensor( [[[ 0 1 2 3 4] [ 5 6 7 8 9]] [[10 11 12 13 14] [15 16 17 18 19]] [[20 21 22 23 24] [25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)
Se você achatar um tensor, pode ver a ordem em que ele está na memória.
# A `-1` passed in the `shape` argument says "Whatever fits".
print(tf.reshape(rank_3_tensor, [-1]))
tf.Tensor( [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29], shape=(30,), dtype=int32)
Normalmente, o único uso razoável de tf.reshape é combinar ou dividir eixos adjacentes (ou adicionar/remover 1 s).
Para este tensor 3x2x5, remodelar para (3x2)x5 ou 3x(2x5) são coisas razoáveis a fazer, pois as fatias não se misturam:
print(tf.reshape(rank_3_tensor, [3*2, 5]), "\n")
print(tf.reshape(rank_3_tensor, [3, -1]))
tf.Tensor( [[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14] [15 16 17 18 19] [20 21 22 23 24] [25 26 27 28 29]], shape=(6, 5), dtype=int32) tf.Tensor( [[ 0 1 2 3 4 5 6 7 8 9] [10 11 12 13 14 15 16 17 18 19] [20 21 22 23 24 25 26 27 28 29]], shape=(3, 10), dtype=int32)
| Algumas boas reformulações. | ||
|---|---|---|
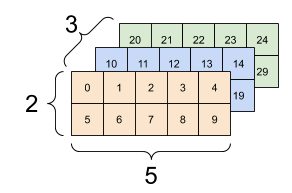 | 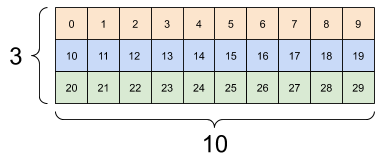 |  |
A remodelação "funcionará" para qualquer nova forma com o mesmo número total de elementos, mas não fará nada útil se você não respeitar a ordem dos eixos.
A troca de eixos em tf.reshape não funciona; você precisa de tf.transpose para isso.
# Bad examples: don't do this
# You can't reorder axes with reshape.
print(tf.reshape(rank_3_tensor, [2, 3, 5]), "\n")
# This is a mess
print(tf.reshape(rank_3_tensor, [5, 6]), "\n")
# This doesn't work at all
try:
tf.reshape(rank_3_tensor, [7, -1])
except Exception as e:
print(f"{type(e).__name__}: {e}")
tf.Tensor( [[[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14]] [[15 16 17 18 19] [20 21 22 23 24] [25 26 27 28 29]]], shape=(2, 3, 5), dtype=int32) tf.Tensor( [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23] [24 25 26 27 28 29]], shape=(5, 6), dtype=int32) InvalidArgumentError: Input to reshape is a tensor with 30 values, but the requested shape requires a multiple of 7 [Op:Reshape]
| Algumas reformulações ruins. | ||
|---|---|---|
 | 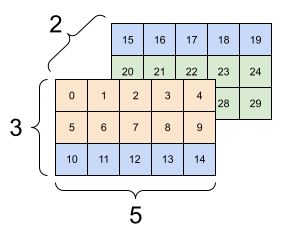 |  |
Você pode se deparar com formas não totalmente especificadas. Ou a forma contém um None (um comprimento de eixo é desconhecido) ou a forma inteira é None (a classificação do tensor é desconhecida).
Exceto para tf.RaggedTensor , essas formas ocorrerão apenas no contexto das APIs simbólicas de criação de gráficos do TensorFlow:
Mais sobre DTypes
Para inspecionar o tipo de dados de um tf.Tensor , use a propriedade Tensor.dtype .
Ao criar um tf.Tensor a partir de um objeto Python, você pode opcionalmente especificar o tipo de dados.
Caso contrário, o TensorFlow escolhe um tipo de dados que pode representar seus dados. O TensorFlow converte números inteiros do Python em tf.int32 e números de ponto flutuante do Python em tf.float32 . Caso contrário, o TensorFlow usa as mesmas regras que o NumPy usa ao converter em arrays.
Você pode transmitir de tipo para tipo.
the_f64_tensor = tf.constant([2.2, 3.3, 4.4], dtype=tf.float64)
the_f16_tensor = tf.cast(the_f64_tensor, dtype=tf.float16)
# Now, cast to an uint8 and lose the decimal precision
the_u8_tensor = tf.cast(the_f16_tensor, dtype=tf.uint8)
print(the_u8_tensor)
tf.Tensor([2 3 4], shape=(3,), dtype=uint8)
Transmissão
Broadcasting é um conceito emprestado do recurso equivalente no NumPy . Resumindo, sob certas condições, tensores menores são "esticados" automaticamente para caber tensores maiores ao executar operações combinadas neles.
O caso mais simples e comum é quando você tenta multiplicar ou adicionar um tensor a um escalar. Nesse caso, o escalar é transmitido para ter a mesma forma que o outro argumento.
x = tf.constant([1, 2, 3])
y = tf.constant(2)
z = tf.constant([2, 2, 2])
# All of these are the same computation
print(tf.multiply(x, 2))
print(x * y)
print(x * z)
tf.Tensor([2 4 6], shape=(3,), dtype=int32) tf.Tensor([2 4 6], shape=(3,), dtype=int32) tf.Tensor([2 4 6], shape=(3,), dtype=int32)
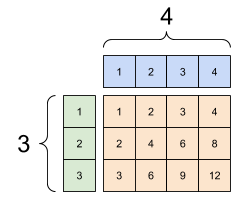
Da mesma forma, eixos com comprimento 1 podem ser estendidos para corresponder aos outros argumentos. Ambos os argumentos podem ser estendidos na mesma computação.
Neste caso, uma matriz 3x1 é multiplicada por elementos por uma matriz 1x4 para produzir uma matriz 3x4. Observe como o 1 inicial é opcional: A forma de y é [4] .
# These are the same computations
x = tf.reshape(x,[3,1])
y = tf.range(1, 5)
print(x, "\n")
print(y, "\n")
print(tf.multiply(x, y))
tf.Tensor( [[1] [2] [3]], shape=(3, 1), dtype=int32) tf.Tensor([1 2 3 4], shape=(4,), dtype=int32) tf.Tensor( [[ 1 2 3 4] [ 2 4 6 8] [ 3 6 9 12]], shape=(3, 4), dtype=int32)
Um add transmitido: um [3, 1] vezes um [1, 4] dá um [3,4] |
|---|
 |
Aqui está a mesma operação sem transmissão:
x_stretch = tf.constant([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
y_stretch = tf.constant([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
print(x_stretch * y_stretch) # Again, operator overloading
tf.Tensor( [[ 1 2 3 4] [ 2 4 6 8] [ 3 6 9 12]], shape=(3, 4), dtype=int32)
Na maioria das vezes, a transmissão é eficiente em termos de tempo e espaço, pois a operação de transmissão nunca materializa os tensores expandidos na memória.
Você vê como é a transmissão usando tf.broadcast_to .
print(tf.broadcast_to(tf.constant([1, 2, 3]), [3, 3]))
tf.Tensor( [[1 2 3] [1 2 3] [1 2 3]], shape=(3, 3), dtype=int32)
Ao contrário de uma operação matemática, por exemplo, broadcast_to não faz nada de especial para economizar memória. Aqui, você está materializando o tensor.
Pode ficar ainda mais complicado. Esta seção do livro Python Data Science Handbook de Jake VanderPlas mostra mais truques de transmissão (novamente no NumPy).
tf.convert_to_tensor
A maioria das operações, como tf.matmul e tf.reshape , recebe argumentos da classe tf.Tensor . No entanto, você notará no caso acima, objetos Python em forma de tensores são aceitos.
A maioria, mas não todas, as operações chamam convert_to_tensor em argumentos não tensores. Existe um registro de conversões, e a maioria das classes de objetos como NumPy's ndarray , TensorShape , Python lists e tf.Variable serão todas convertidas automaticamente.
Veja tf.register_tensor_conversion_function para mais detalhes, e se você tiver seu próprio tipo, você gostaria de converter automaticamente para um tensor.
Tensores irregulares
Um tensor com números variáveis de elementos ao longo de algum eixo é chamado de "ragged". Use tf.ragged.RaggedTensor para dados irregulares.
Por exemplo, Isso não pode ser representado como um tensor regular:
A tf.RaggedTensor , forma: [4, None] |
|---|
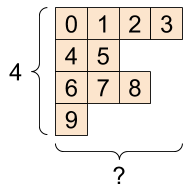 |
ragged_list = [
[0, 1, 2, 3],
[4, 5],
[6, 7, 8],
[9]]
try:
tensor = tf.constant(ragged_list)
except Exception as e:
print(f"{type(e).__name__}: {e}")
ValueError: Can't convert non-rectangular Python sequence to Tensor.
Em vez disso, crie um tf.RaggedTensor usando tf.ragged.constant :
ragged_tensor = tf.ragged.constant(ragged_list)
print(ragged_tensor)
<tf.RaggedTensor [[0, 1, 2, 3], [4, 5], [6, 7, 8], [9]]>
A forma de um tf.RaggedTensor conterá alguns eixos com comprimentos desconhecidos:
print(ragged_tensor.shape)
(4, None)
Tensores de string
tf.string é um dtype , o que significa que você pode representar dados como strings (matrizes de bytes de comprimento variável) em tensores.
As strings são atômicas e não podem ser indexadas como as strings do Python. O comprimento da corda não é um dos eixos do tensor. Veja tf.strings para funções para manipulá-los.
Aqui está um tensor de string escalar:
# Tensors can be strings, too here is a scalar string.
scalar_string_tensor = tf.constant("Gray wolf")
print(scalar_string_tensor)
tf.Tensor(b'Gray wolf', shape=(), dtype=string)
E um vetor de strings:
Um vetor de strings, forma: [3,] |
|---|
 |
# If you have three string tensors of different lengths, this is OK.
tensor_of_strings = tf.constant(["Gray wolf",
"Quick brown fox",
"Lazy dog"])
# Note that the shape is (3,). The string length is not included.
print(tensor_of_strings)
tf.Tensor([b'Gray wolf' b'Quick brown fox' b'Lazy dog'], shape=(3,), dtype=string)
Na impressão acima, o prefixo b indica que tf.string dtype não é uma string unicode, mas uma string de bytes. Consulte o Tutorial Unicode para saber mais sobre como trabalhar com texto unicode no TensorFlow.
Se você passar caracteres unicode, eles serão codificados em utf-8.
tf.constant("🥳👍")
<tf.Tensor: shape=(), dtype=string, numpy=b'\xf0\x9f\xa5\xb3\xf0\x9f\x91\x8d'>
Algumas funções básicas com strings podem ser encontradas em tf.strings , incluindo tf.strings.split .
# You can use split to split a string into a set of tensors
print(tf.strings.split(scalar_string_tensor, sep=" "))
tf.Tensor([b'Gray' b'wolf'], shape=(2,), dtype=string)
# ...but it turns into a `RaggedTensor` if you split up a tensor of strings,
# as each string might be split into a different number of parts.
print(tf.strings.split(tensor_of_strings))
<tf.RaggedTensor [[b'Gray', b'wolf'], [b'Quick', b'brown', b'fox'], [b'Lazy', b'dog']]>
Três cordas divididas, forma: [3, None] |
|---|
 |
E tf.string.to_number :
text = tf.constant("1 10 100")
print(tf.strings.to_number(tf.strings.split(text, " ")))
tf.Tensor([ 1. 10. 100.], shape=(3,), dtype=float32)
Embora você não possa usar tf.cast para transformar um tensor de string em números, você pode convertê-lo em bytes e depois em números.
byte_strings = tf.strings.bytes_split(tf.constant("Duck"))
byte_ints = tf.io.decode_raw(tf.constant("Duck"), tf.uint8)
print("Byte strings:", byte_strings)
print("Bytes:", byte_ints)
Byte strings: tf.Tensor([b'D' b'u' b'c' b'k'], shape=(4,), dtype=string) Bytes: tf.Tensor([ 68 117 99 107], shape=(4,), dtype=uint8)
# Or split it up as unicode and then decode it
unicode_bytes = tf.constant("アヒル 🦆")
unicode_char_bytes = tf.strings.unicode_split(unicode_bytes, "UTF-8")
unicode_values = tf.strings.unicode_decode(unicode_bytes, "UTF-8")
print("\nUnicode bytes:", unicode_bytes)
print("\nUnicode chars:", unicode_char_bytes)
print("\nUnicode values:", unicode_values)
Unicode bytes: tf.Tensor(b'\xe3\x82\xa2\xe3\x83\x92\xe3\x83\xab \xf0\x9f\xa6\x86', shape=(), dtype=string) Unicode chars: tf.Tensor([b'\xe3\x82\xa2' b'\xe3\x83\x92' b'\xe3\x83\xab' b' ' b'\xf0\x9f\xa6\x86'], shape=(5,), dtype=string) Unicode values: tf.Tensor([ 12450 12498 12523 32 129414], shape=(5,), dtype=int32)
O tf.string tf.string é usado para todos os dados de bytes brutos no TensorFlow. O módulo tf.io contém funções para converter dados de e para bytes, incluindo decodificação de imagens e análise de csv.
Tensores esparsos
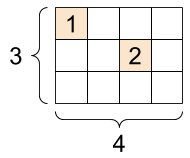
Às vezes, seus dados são escassos, como um espaço de incorporação muito amplo. O TensorFlow oferece suporte a tf.sparse.SparseTensor e operações relacionadas para armazenar dados esparsos com eficiência.
A tf.SparseTensor , forma: [3, 4] |
|---|
 |
# Sparse tensors store values by index in a memory-efficient manner
sparse_tensor = tf.sparse.SparseTensor(indices=[[0, 0], [1, 2]],
values=[1, 2],
dense_shape=[3, 4])
print(sparse_tensor, "\n")
# You can convert sparse tensors to dense
print(tf.sparse.to_dense(sparse_tensor))
SparseTensor(indices=tf.Tensor( [[0 0] [1 2]], shape=(2, 2), dtype=int64), values=tf.Tensor([1 2], shape=(2,), dtype=int32), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64)) tf.Tensor( [[1 0 0 0] [0 0 2 0] [0 0 0 0]], shape=(3, 4), dtype=int32)
