 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir sur GitHub Voir sur GitHub |  Télécharger le cahier Télécharger le cahier |  Voir le modèle TF Hub Voir le modèle TF Hub |
Ce Colab démontre l'utilisation d'un module TF Hub basé sur un réseau accusatoire génératif (GAN). Le module mappe des vecteurs à N dimensions, appelés espace latent, aux images RVB.
Deux exemples sont fournis :
- La cartographie de l' espace latent aux images, et
- Étant donné une image cible, en utilisant la descente de gradient pour trouver un vecteur latent qui génère une image similaire à l'image cible.
Prérequis facultatifs
- Familiarité avec faible niveau des concepts tensorflow .
- Générative accusatoire Réseau sur Wikipédia.
- Document Progressive GAN: progressive croissante de GAN pour la qualité améliorée, la stabilité et la variation .
Plus de modèles
Ici vous pouvez trouver tous les modèles actuellement hébergés sur tfhub.dev qui peut générer des images.
Installer
# Install imageio for creating animations.pip -q install imageiopip -q install scikit-imagepip install git+https://github.com/tensorflow/docs
Importations et définitions de fonctions
from absl import logging
import imageio
import PIL.Image
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
tf.random.set_seed(0)
import tensorflow_hub as hub
from tensorflow_docs.vis import embed
import time
try:
from google.colab import files
except ImportError:
pass
from IPython import display
from skimage import transform
# We could retrieve this value from module.get_input_shapes() if we didn't know
# beforehand which module we will be using.
latent_dim = 512
# Interpolates between two vectors that are non-zero and don't both lie on a
# line going through origin. First normalizes v2 to have the same norm as v1.
# Then interpolates between the two vectors on the hypersphere.
def interpolate_hypersphere(v1, v2, num_steps):
v1_norm = tf.norm(v1)
v2_norm = tf.norm(v2)
v2_normalized = v2 * (v1_norm / v2_norm)
vectors = []
for step in range(num_steps):
interpolated = v1 + (v2_normalized - v1) * step / (num_steps - 1)
interpolated_norm = tf.norm(interpolated)
interpolated_normalized = interpolated * (v1_norm / interpolated_norm)
vectors.append(interpolated_normalized)
return tf.stack(vectors)
# Simple way to display an image.
def display_image(image):
image = tf.constant(image)
image = tf.image.convert_image_dtype(image, tf.uint8)
return PIL.Image.fromarray(image.numpy())
# Given a set of images, show an animation.
def animate(images):
images = np.array(images)
converted_images = np.clip(images * 255, 0, 255).astype(np.uint8)
imageio.mimsave('./animation.gif', converted_images)
return embed.embed_file('./animation.gif')
logging.set_verbosity(logging.ERROR)
Interpolation de l'espace latent
Vecteurs aléatoires
Interpolation spatiale latente entre deux vecteurs initialisés aléatoirement. Nous utiliserons un module Hub TF PROGAN-128 qui contient un progressif pré-formé GAN.
progan = hub.load("https://tfhub.dev/google/progan-128/1").signatures['default']
def interpolate_between_vectors():
v1 = tf.random.normal([latent_dim])
v2 = tf.random.normal([latent_dim])
# Creates a tensor with 25 steps of interpolation between v1 and v2.
vectors = interpolate_hypersphere(v1, v2, 50)
# Uses module to generate images from the latent space.
interpolated_images = progan(vectors)['default']
return interpolated_images
interpolated_images = interpolate_between_vectors()
animate(interpolated_images)

Trouver le vecteur le plus proche dans l'espace latent
Corrigez une image cible. À titre d'exemple, utilisez une image générée à partir du module ou téléchargez la vôtre.
image_from_module_space = True # @param { isTemplate:true, type:"boolean" }
def get_module_space_image():
vector = tf.random.normal([1, latent_dim])
images = progan(vector)['default'][0]
return images
def upload_image():
uploaded = files.upload()
image = imageio.imread(uploaded[list(uploaded.keys())[0]])
return transform.resize(image, [128, 128])
if image_from_module_space:
target_image = get_module_space_image()
else:
target_image = upload_image()
display_image(target_image)

Après avoir défini une fonction de perte entre l'image cible et l'image générée par une variable d'espace latent, nous pouvons utiliser la descente de gradient pour trouver des valeurs de variables qui minimisent la perte.
tf.random.set_seed(42)
initial_vector = tf.random.normal([1, latent_dim])
display_image(progan(initial_vector)['default'][0])

def find_closest_latent_vector(initial_vector, num_optimization_steps,
steps_per_image):
images = []
losses = []
vector = tf.Variable(initial_vector)
optimizer = tf.optimizers.Adam(learning_rate=0.01)
loss_fn = tf.losses.MeanAbsoluteError(reduction="sum")
for step in range(num_optimization_steps):
if (step % 100)==0:
print()
print('.', end='')
with tf.GradientTape() as tape:
image = progan(vector.read_value())['default'][0]
if (step % steps_per_image) == 0:
images.append(image.numpy())
target_image_difference = loss_fn(image, target_image[:,:,:3])
# The latent vectors were sampled from a normal distribution. We can get
# more realistic images if we regularize the length of the latent vector to
# the average length of vector from this distribution.
regularizer = tf.abs(tf.norm(vector) - np.sqrt(latent_dim))
loss = target_image_difference + regularizer
losses.append(loss.numpy())
grads = tape.gradient(loss, [vector])
optimizer.apply_gradients(zip(grads, [vector]))
return images, losses
num_optimization_steps=200
steps_per_image=5
images, loss = find_closest_latent_vector(initial_vector, num_optimization_steps, steps_per_image)
.................................................................................................... ....................................................................................................
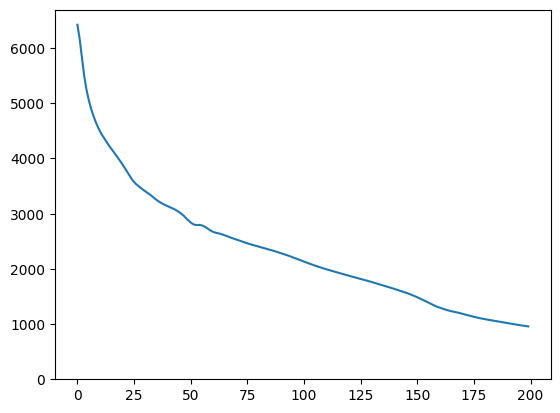
plt.plot(loss)
plt.ylim([0,max(plt.ylim())])
(0.0, 6696.301751708985)
animate(np.stack(images))

Comparez le résultat à la cible :
display_image(np.concatenate([images[-1], target_image], axis=1))

Jouer avec l'exemple ci-dessus
Si l'image provient de l'espace du module, la descente est rapide et converge vers un échantillon raisonnable. Essayez descendant à une image qui ne sont pas de l'espace du module. La descente ne convergera que si l'image est raisonnablement proche de l'espace des images d'entraînement.
Comment le faire descendre plus vite et vers une image plus réaliste ? On peut essayer :
- en utilisant une perte différente sur la différence d'image, par exemple quadratique,
- en utilisant un régularisateur différent sur le vecteur latent,
- initialisation à partir d'un vecteur aléatoire en plusieurs exécutions,
- etc.
