Zobacz na TensorFlow.org

Uruchom w Google Colab

Wyświetl źródło na GitHub

Pobierz notatnik

TensorFlow Probability (TFP) w JAX ma teraz narzędzia do rozproszonych obliczeń numerycznych. Aby skalować do dużej liczby akceleratorów, narzędzia zbudowane są wokół pisania kodu przy użyciu paradygmatu „pojedynczy program wielu danych”, w skrócie SPMD.

W tym notatniku omówimy, jak „myśleć w SPMD” i wprowadzimy nowe abstrakcje TFP do skalowania do konfiguracji, takich jak moduły TPU lub klastry procesorów graficznych. Jeśli sam uruchamiasz ten kod, wybierz środowisko wykonawcze TPU.

Najpierw zainstalujemy najnowsze wersje TFP, JAX i TF.

Instaluje

pip install jaxlib --upgrade -q 2>&1 1> /dev/null
pip install tfp-nightly[jax] --upgrade -q 2>&1 1> /dev/null
pip install tf-nightly-cpu -q -I 2>&1 1> /dev/null
pip install jax -I -q --upgrade 2>&1 1>/dev/null

Zaimportujemy kilka ogólnych bibliotek wraz z kilkoma narzędziami JAX.

Konfiguracja i import

import functools
import collections
import contextlib

import jax
import jax.numpy as jnp
from jax import lax
from jax import random
import jax.numpy as jnp

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow_datasets as tfds

from tensorflow_probability.substrates import jax as tfp

sns.set(style='white')

INFO:tensorflow:Enabling eager execution
INFO:tensorflow:Enabling v2 tensorshape
INFO:tensorflow:Enabling resource variables
INFO:tensorflow:Enabling tensor equality
INFO:tensorflow:Enabling control flow v2

Skonfigurujemy również kilka przydatnych aliasów TFP. Nowe abstrakcje są obecnie zawarte w tfp.experimental.distribute i tfp.experimental.mcmc .

tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc

Root = tfed.JointDistributionCoroutine.Root

Aby podłączyć notebook do TPU, używamy następującego pomocnika firmy JAX. Aby potwierdzić, że jesteśmy połączeni, wypisujemy liczbę urządzeń, która powinna wynosić osiem.

from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')

Found 8 devices

Szybkie wprowadzenie do jax.pmap

Po podłączeniu do TPU, mamy dostęp do ośmiu urządzeń. Jednak, gdy chętnie uruchamiamy kod JAX, JAX domyślnie uruchamia obliczenia tylko na jednym.

Najprostszym sposobem wykonywania obliczeń na wielu urządzeniach jest mapowanie funkcji, przy czym każde urządzenie wykonuje jeden indeks mapy. JAX zapewnia jax.pmap ( „Mapa”) równolegle transformację, która zamienia się w jedną funkcję, która odwzorowuje funkcji na kilku urządzeniach.

W poniższym przykładzie tworzymy tablicę o rozmiarze 8 (aby dopasować liczbę dostępnych urządzeń) i mapujemy funkcję, która dodaje do niej 5.

xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)

<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5.  6.  7.  8.  9. 10. 11. 12.]

Należy pamiętać, że otrzymujemy ShardedDeviceArray typu plecami, wskazując, że tablica wyjściowa jest fizycznie podzielony na różnych urządzeniach.

jax.pmap działa semantycznie jak mapa, ale ma kilka istotnych opcji, które modyfikują swoje zachowanie. Domyślnie pmap zakłada, wszystkie wejścia do funkcji są odwzorowywane na, ale możemy to zmienić, z in_axes argument.

xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)

[ 5.  6.  7.  8.  9. 10. 11. 12.]

Analogicznie, out_axes argument pmap określa, czy nie wrócić do wartości, na każdym urządzeniu. Ustawianie out_axes do None automatycznie zwraca wartość na 1. urządzenia i powinno być używane tylko wtedy, gdy mamy pewność, że wartości są takie same na każdym urządzeniu.

xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)

2.0

Co się dzieje, gdy to, co chcielibyśmy zrobić, nie jest łatwe do wyrażenia jako zmapowana czysta funkcja? Na przykład, co jeśli chcielibyśmy zsumować na osi, na której mapujemy? JAX oferuje "zbiory", funkcje, które komunikują się między urządzeniami, aby umożliwić pisanie ciekawszych i bardziej złożonych programów rozproszonych. Aby zrozumieć, jak dokładnie działają, wprowadzimy SPMD.

Co to jest SPMD?

Pojedynczy program wielu danych (SPMD) to współbieżny model programowania, w którym pojedynczy program (tj. ten sam kod) jest wykonywany jednocześnie na różnych urządzeniach, ale dane wejściowe do każdego z uruchomionych programów mogą się różnić.

Jeśli nasz program jest prostą funkcją jej wejść (czyli coś jak x + 5 ), uruchomiony program w sPmd właśnie odwzorowanie go na różne dane, tak jak my z jax.pmap wcześniej. Możemy jednak zrobić coś więcej niż tylko „mapować” funkcję. JAX oferuje „zbiory”, czyli funkcje, które komunikują się między urządzeniami.

Na przykład może chcielibyśmy zmierzyć sumę ilości na wszystkich naszych urządzeniach. Zanim to zrobimy, musimy przypisać nazwę do osi jesteśmy mapowanie nad w pmap . Następnie używamy lax.psum ( „Sum”) równolegle do wykonywania funkcji sumy różnych urządzeniach, zapewniając nam zidentyfikować nazwie oś jesteśmy zsumowanie.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)

ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)

psum agregaty zbiorowe wartości x na każdym urządzeniu i synchronizuje jego wartość po mapie tj out jest 28. na każdym urządzeniu. Nie wykonujemy już prostej „mapy”, ale wykonujemy program SPMD, w którym obliczenia każdego urządzenia mogą teraz wchodzić w interakcje z tymi samymi obliczeniami na innych urządzeniach, choć w ograniczony sposób przy użyciu kolektywów. W tym scenariuszu, możemy użyć out_axes = None , ponieważ psum zsynchronizuje wartość.

def f(x):
  out = lax.psum(x, axis_name='i')
  return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))

ShardedDeviceArray(28., dtype=float32)

SPMD umożliwia nam napisanie jednego programu, który jest uruchamiany na każdym urządzeniu w dowolnej konfiguracji TPU jednocześnie. Ten sam kod, który jest używany do uczenia maszynowego na 8 rdzeniach TPU, może być użyty w module TPU, który może mieć setki, a nawet tysiące rdzeni! W celu bardziej szczegółowego poradnika o jax.pmap i sPmd, można zwrócić się do The JAX 101 tutorialu .

MCMC na dużą skalę

W tym zeszycie skupimy się na wykorzystaniu metod Markowa Łańcucha Monte Carlo (MCMC) do wnioskowania bayesowskiego. Istnieje wiele sposobów wykorzystania wielu urządzeń do obsługi MCMC, ale w tym notebooku skupimy się na dwóch:

1. Uruchamianie niezależnych łańcuchów Markowa na różnych urządzeniach. Ten przypadek jest dość prosty i można go zrobić z waniliowym TFP.
2. Dzielenie zbioru danych na fragmenty na różnych urządzeniach. Ta sprawa jest nieco bardziej złożona i wymaga niedawno dodanego sprzętu TFP.

Niezależne łańcuchy

Powiedzmy, że chcielibyśmy przeprowadzić wnioskowanie bayesowskie dotyczące problemu za pomocą MCMC i chcielibyśmy uruchomić kilka łańcuchów równolegle na kilku urządzeniach (powiedzmy 2 na każdym urządzeniu). Okazuje się, że jest to program, który możemy po prostu „mapować” na różnych urządzeniach, czyli taki, który nie potrzebuje kolektywów. Aby upewnić się, że każdy program wykonuje inny łańcuch Markowa (w przeciwieństwie do uruchamiania tego samego), przekazujemy inną wartość dla losowego ziarna do każdego urządzenia.

Wypróbujmy to z zabawkowym problemem próbkowania z dwuwymiarowego rozkładu Gaussa. Możemy wykorzystać istniejącą funkcjonalność MCMC TFP po wyjęciu z pudełka. Ogólnie rzecz biorąc, staramy się umieścić większość logiki w naszej mapowanej funkcji, aby wyraźniej rozróżnić między tym, co działa na wszystkich urządzeniach, a tylko na pierwszym.

def run(seed):
  target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob

  initial_state = jnp.zeros([2, 2]) # 2 chains
  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
  def trace_fn(state, pkr):
    return target_log_prob(state)

  states, log_prob = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    kernel=kernel,
    current_state=initial_state,
    trace_fn=trace_fn,
    seed=seed
  )
  return states, log_prob

By sobie, run funkcja przyjmuje w bezpaństwowym losowej nasion (aby zobaczyć, jak bezpaństwowcem pracę losowości można przeczytać TFP na JAX notebooka lub zobacz poradnik JAX 101 ). Mapowanie run przez różnych nasion spowoduje działa kilka niezależnych łańcuchów Markowa.

states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)

(8, 1000, 2, 2) (8, 1000, 2)

Zwróć uwagę, że mamy teraz dodatkową oś odpowiadającą każdemu urządzeniu. Możemy zmienić rozmieszczenie wymiarów i spłaszczyć je, aby uzyskać oś dla 16 łańcuchów.

states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])

fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()

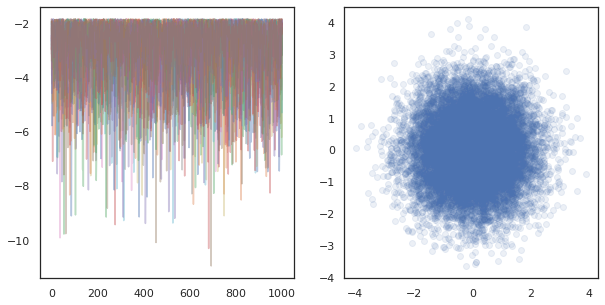
Uruchamiając niezależne łańcuchy na wielu urządzeniach, jest to tak proste jak pmap -ing na funkcję, która używa tfp.mcmc , zapewniające mijamy różne wartości dla losowego nasion do każdego urządzenia.

Podział danych

Kiedy wykonujemy MCMC, rozkład docelowy jest często rozkładem a posteriori uzyskanym przez warunkowanie na zbiorze danych, a obliczenie nieznormalizowanej gęstości logarytmicznej obejmuje sumowanie prawdopodobieństw dla każdego zaobserwowanego danych.

W przypadku bardzo dużych zbiorów danych uruchomienie nawet jednego łańcucha na jednym urządzeniu może być zbyt kosztowne. Jednak gdy mamy dostęp do wielu urządzeń, możemy podzielić zbiór danych na urządzenia, aby lepiej wykorzystać dostępne obliczenia.

Jeśli chcielibyśmy zrobić MCMC z sharded zbioru danych, musimy upewnić się, że nieznormalizowanych dziennika gęstość obliczamy na każdym urządzeniu reprezentuje sumę, czyli gęstość we wszystkich danych, w przeciwnym razie każde urządzenie będzie robić MCMC z własnej niewłaściwej tarczy dystrybucja. W tym celu TFP ma teraz nowe narzędzia (tj tfp.experimental.distribute i tfp.experimental.mcmc ), które pozwalają computing „sharded” prawdopodobieństw dziennika i robi MCMC z nimi.

Dystrybucje podzielone na fragmenty

Rdzeń abstrakcji TFP zapewnia teraz do obliczania sharded probabiliities dziennika jest Sharded meta-dystrybucji, który zajmuje się dystrybucją na wejściu i zwraca nowy rozkład, który ma szczególne właściwości, gdy są wykonywane w kontekście sPmd. Sharded mieszka w tfp.experimental.distribute .

Intuicyjnie Sharded odpowiada dystrybucji do zestawu zmiennych losowych, które zostały „split” na różnych urządzeniach. Na każdym urządzeniu wytworzą różne próbki i mogą indywidualnie mieć różne gęstości logarytmiczne. Alternatywnie Sharded odpowiada dystrybucji do „płytki” w terminologii graficznego wzoru, gdy rozmiar płyty jest liczba urządzeń.

Próbkowanie Sharded dystrybucji

Gdybyśmy próbki od Normal rozkładu w programie samopoczucia pmap -ED przy użyciu tego samego materiału siewnego na każdym urządzeniu, będziemy mieli taką samą próbkę na każdym urządzeniu. Poniższą funkcję możemy traktować jako próbkowanie pojedynczej zmiennej losowej zsynchronizowanej między urządzeniami.

# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
  return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                    -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32)

Jeśli będziemy zawijać tfd.Normal(0., 1.) z tfed.Sharded , możemy logicznie teraz mają osiem różnych zmiennych losowych (po jednym z każdego urządzenia) i dlatego będzie produkować różne próbki do każdego z nich, mimo przekazując tym samym materiałem siewnym .

def f(seed, _):
  return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

ShardedDeviceArray([ 1.2152631 ,  0.7818249 ,  0.32549605,  0.6828047 ,
                     1.3973192 , -0.57830244,  0.37862757,  2.7706041 ],                   dtype=float32)

Równoważną reprezentacją tego rozkładu na pojedynczym urządzeniu jest tylko 8 niezależnych próbek normalnych. Mimo że wartość próbki będą różne ( tfed.Sharded robi pseudolosowych generowania liczb nieco inaczej), obaj reprezentują ten sam rozkład.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))

DeviceArray([ 0.08086783, -0.38624594, -0.3756545 ,  1.668957  ,
             -1.2758069 ,  2.1192007 , -0.85821325,  1.1305912 ],            dtype=float32)

Biorąc logarytm gęstości Sharded dystrybucji

Zobaczmy, co się stanie, gdy obliczymy gęstość logarytmiczną próbki ze zwykłej dystrybucji w kontekście SPMD.

def f(seed, _):
  dist = tfd.Normal(0., 1.)
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))

(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
                     -0.20584236, -0.20584236, -0.20584236, -0.20584236],                   dtype=float32),
 ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
                     -0.94012403, -0.94012403, -0.94012403, -0.94012403],                   dtype=float32))

Każda próbka jest taka sama na każdym urządzeniu, więc obliczamy tę samą gęstość również na każdym urządzeniu. Intuicyjnie mamy tutaj tylko rozkład dla jednej zmiennej o rozkładzie normalnym.

Z Sharded dystrybucji, mamy rozkład na 8 zmiennych losowych, więc kiedy obliczamy log_prob próbki, możemy podsumować, na różnych urządzeniach, na każdym z poszczególnych gęstościach dziennika. (Możesz zauważyć, że ta całkowita wartość log_prob jest większa niż obliczona powyżej pojedyncza wartość log_prob).

def f(seed, _):
  dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
    random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)

Sample: [ 1.2152631   0.7818249   0.32549605  0.6828047   1.3973192  -0.57830244
  0.37862757  2.7706041 ]
Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205
 -13.7349205 -13.7349205]

Równoważna dystrybucja „niepodzielona” daje taką samą gęstość dziennika.

dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)

DeviceArray(-13.7349205, dtype=float32)

Sharded dystrybucja produkuje różne wartości z sample na każdym urządzeniu, ale dostać taką samą wartość dla log_prob na każdym urządzeniu. Co tu się dzieje? Sharded dystrybucja robi psum wewnętrznie, aby zapewnić log_prob wartości są zsynchronizowane różnych urządzeniach. Dlaczego mielibyśmy chcieć takiego zachowania? Jeśli używasz tego samego łańcucha MCMC na każdym urządzeniu, chcielibyśmy się target_log_prob być taka sama w całej każdego urządzenia, nawet jeśli niektóre zmienne losowe w obliczeniach są sharded różnych urządzeniach.

Ponadto u Sharded zapewnia rozdział że gradienty między urządzeniami są prawidłowe, w celu zapewnienia, że algorytmy jak HMC które biorą gradienty Funkcja rejestru gęstości jako część funkcji przejściowej wytwarzają odpowiednie próbki.

Sharded JointDistribution s

Możemy tworzyć modele z wieloma Sharded zmiennych losowych za pomocą JointDistribution s (JDs). Niestety, Sharded dystrybucje nie może być bezpiecznie stosowany z wanilii tfd.JointDistribution s, ale tfp.experimental.distribute eksport „połatany” JDS że będzie się zachowywał jak Sharded dystrybucji.

def f(seed, _):
  dist = tfed.JointDistributionSequential([
    tfd.Normal(0., 1.),
    tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
  ])
  x = dist.sample(seed=seed)
  return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))

([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
                      1.6121525, 1.6121525, 1.6121525], dtype=float32),
  ShardedDeviceArray([ 0.8690128 , -0.83167845,  1.2209264 ,  0.88412696,
                       0.76478404, -0.66208494, -0.0129658 ,  0.7391483 ],                   dtype=float32)],
 ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
                     -12.214451, -12.214451, -12.214451, -12.214451],                   dtype=float32))

Te sharded JDs może mieć zarówno Sharded dystrybucje i wanilia TFP jak składniki. Dla dystrybucji niesharded otrzymujemy tę samą próbkę na każdym urządzeniu, a dla dystrybucji sharded otrzymujemy różne próbki. log_prob na każdym urządzeniu jest zsynchronizowany, jak również.

MCMC z Sharded rozkładów

Jak myślimy o Sharded dystrybucji w kontekście MCMC? Jeśli mamy generatywny model, który może być wyrażona jako JointDistribution , możemy odebrać jakąś oś tego modelu do „odłamek” po drugiej stronie. Zazwyczaj jedna zmienna losowa w modelu będzie odpowiadać obserwowanym danym, a jeśli mamy duży zestaw danych, który chcielibyśmy podzielić na różne urządzenia, chcemy, aby zmienne skojarzone z punktami danych również zostały podzielone. Możemy również mieć „lokalne” zmienne losowe, które są jeden do jednego z obserwacjami, które shardujemy, więc będziemy musieli dodatkowo shardować te zmienne losowe.

Pójdziemy na przykłady użycia Sharded rozkładów z TFP MCMC w tej sekcji. Zaczniemy prostszym przykładzie regresji logistycznej Bayesa i zawarcia z przykładu faktoryzacji macierzy, w celu wykazania kilka przypadków użycia dla distribute biblioteki.

Przykład: Bayesowska regresja logistyczna dla MNIST

Chcielibyśmy wykonać Bayesowska regresję logistyczną na dużym zbiorze danych; model ten uprzedniego \(p(\theta)\) nad wag regresji, a prawdopodobieństwo \(p(y_i | \theta, x_i)\) że sumuje się wszystkimi danymi \(\{x_i, y_i\}_{i = 1}^N\) do otrzymania całkowitej gęstości stawów dziennika. Gdybyśmy shard nasze dane, chcielibyśmy shard obserwowanych zmiennych losowych \(x_i\) i \(y_i\) w naszym modelu.

Do klasyfikacji MNIST stosujemy następujący bayesowski model regresji logistycznej:

\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]

Załadujmy MNIST za pomocą zestawów danych TensorFlow.

mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.

raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.

Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1...
WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your
local data directory. If you'd instead prefer to read directly from our public
GCS bucket (recommended if you're running on GCP), you can instead pass
`try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`.
HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio…
Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.

Mamy 60000 obrazów treningowych, ale wykorzystajmy nasze 8 dostępnych rdzeni i podzielmy je na 8 sposobów. Będziemy korzystać z tej wygodnej shard funkcję użytkową.

def shard_value(x):
  x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
  return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices

shard = functools.partial(jax.tree_map, shard_value)

sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)

(8, 7500, 784) (8, 7500)

Zanim przejdziemy dalej, szybko omówmy precyzję w TPU i jej wpływ na konsolę HMC. TPU wykonać mnożenie macierzy za pomocą niskiej bfloat16 precyzji dla szybkości. bfloat16 mnożenie macierzy są często wystarczające dla wielu zastosowań głębokiego uczenia się, ale gdy używana z HMC mamy empirycznie stwierdzono niższe precyzji może prowadzić do rozbieżnych trajektoriach, powoduje odrzucenie. Możemy użyć mnożenia macierzy o wyższej precyzji, kosztem dodatkowych obliczeń.

Aby zwiększyć precyzję matmul, możemy użyć jax.default_matmul_precision dekorator z "tensorfloat32" precyzją (dla jeszcze większej precyzji możemy użyć "float32" precyzja).

Załóżmy teraz zdefiniować naszą run funkcji, które odbędzie się w losowej nasion (które będą takie same na każdym urządzeniu) i odłamek MNIST. Funkcja zaimplementuje wspomniany model, a następnie użyjemy waniliowej funkcjonalności MCMC TFP do uruchomienia pojedynczego łańcucha. Będziemy upewnić ozdobić run z jax.default_matmul_precision dekoratora aby upewnić się, że mnożenie macierzy jest prowadzony z większą precyzją, chociaż w tym konkretnym przykładzie poniżej, możemy równie dobrze użyć jnp.dot(images, w, precision=lax.Precision.HIGH) .

# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device. 
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
  images, labels = data # a sharded dataset
  num_examples, dim = images.shape
  num_classes = 10

  def model_fn():
    w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
    b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
    logits = jnp.dot(images, w) + b
    yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
                       shard_axis_name='data')
  model = tfed.JointDistributionCoroutine(model_fn)

  init_seed, sample_seed = random.split(seed)

  initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`

  def target_log_prob(*state):
    return model.log_prob((*state, labels))

  def accuracy(w, b):
    logits = images.dot(w) + b
    preds = logits.argmax(axis=-1)
    # We take the average accuracy across devices by using `lax.pmean`
    return lax.pmean((preds == labels).mean(), 'data')

  kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
  kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
  def trace_fn(state, pkr):
    return (
        target_log_prob(*state),
        accuracy(*state),
        pkr.new_step_size)
  states, trace = tfm.sample_chain(
    num_results=1000,
    num_burnin_steps=1000,
    current_state=initial_state,
    kernel=kernel,
    trace_fn=trace_fn,
    seed=sample_seed
  )
  return states, trace

jax.pmap zawiera kompilacji JIT ale funkcja zestawiane są buforowane po pierwszej rozmowy. Zadzwonimy run i ignorować wyjście cache kompilację.

%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s
Wall time: 1min 54s

Będziemy dziś nazywamy run ponownie, aby zobaczyć, jak długo faktyczna realizacja trwa.

%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s
Wall time: 1min 43s

Wykonujemy 200 000 kroków przeskoku, z których każdy oblicza gradient w całym zbiorze danych. Podział obliczeń na 8 rdzeni pozwala nam obliczyć odpowiednik 200 000 epok treningu w około 95 sekund, około 2100 epok na sekundę!

Wykreślmy gęstość logarytmiczną każdej próbki i dokładność każdej próbki:

fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()

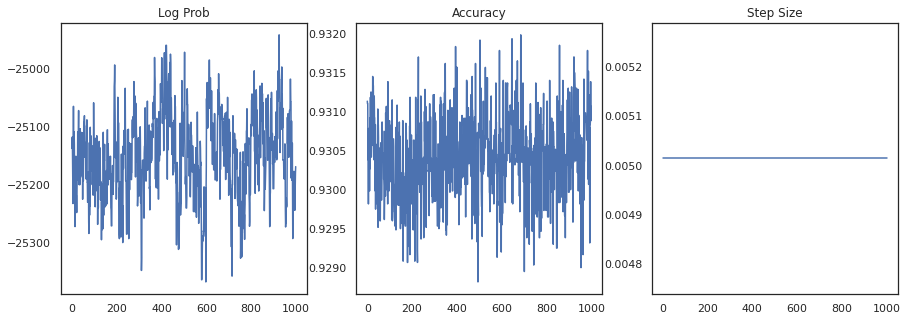
Jeśli połączymy próbki, możemy obliczyć średnią modelu bayesowskiego, aby poprawić naszą wydajność.

@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
  images, labels = data
  logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
  probs = jax.nn.softmax(logits, axis=-1)
  bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
  avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
  return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')

sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')

Average Accuracy: 0.9188529253005981
BMA Accuracy: 0.9264000058174133
Accuracy Improvement: 0.0075470805168151855

Średnia modelu bayesowskiego zwiększa naszą dokładność o prawie 1%!

Przykład: system rekomendacji MovieLens

Spróbujmy teraz przeprowadzić wnioskowanie na podstawie zestawu danych rekomendacji MovieLens, który jest zbiorem użytkowników i ich ocen różnych filmów. W szczególności, możemy reprezentować MovieLens w charakterze \(N \times M\) macierzy zegarek \(W\) gdzie \(N\) jest liczbą użytkowników i \(M\) jest liczbą filmów; oczekujemy \(N > M\). Wpisy \(W_{ij}\) są logiczną wskazującą, czy użytkownik \(i\) oglądał film \(j\). Pamiętaj, że MovieLens zapewnia oceny użytkowników, ale ignorujemy je, aby uprościć problem.

Najpierw załadujemy zbiór danych. Użyjemy wersji z 1 milionem ocen.

movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
          'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
          'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
          'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']

Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0...
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty…
HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl…

HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))
Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord
HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value='')))
Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.

Zrobimy jakieś wstępne przetwarzanie w zbiorze danych w celu uzyskania macierzy zegarek \(W\).

raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']

movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])

num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1

movie_titles = dict(zip(movielens['train']['movie_id'],
                        movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
                        genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
                     for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]

watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)

(6040, 3706)

Można zdefiniować generatywny model \(W\)za pomocą prostego modelu faktoryzacji macierzy probabilistyczne. Zakładamy utajony \(N \times D\) macierzy użytkownik \(U\) i utajony \(M \times D\) matrycowy film \(V\), która po pomnożeniu produkować logits o Bernoulliego dla macierzy zegarek \(W\). Będziemy także do wektory polaryzacji dla użytkowników, jak i filmów, \(u\) i \(v\).

\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]

To dość duża macierz; 6040 użytkowników i 3706 filmów prowadzi do matrycy z ponad 22 milionami wpisów. Jak podchodzimy do shardingu tego modelu? Dobrze, jeśli założymy, że \(N > M\) (czyli istnieje więcej użytkowników niż w filmach), wtedy byłoby sensu shard matrycę zegarek poprzek osi użytkownika, więc każde urządzenie miałoby kawałek matrycy zegarek odpowiedni do podzbioru użytkowników . W przeciwieństwie do poprzedniego przykładu, jednak będziemy również musieli shard górę \(U\) matrycę, ponieważ ma osadzanie dla każdego użytkownika, więc każde urządzenie będzie odpowiedzialny za odłamek \(U\) i odłamek \(W\). Z drugiej strony, \(V\) będzie unsharded i być synchronizowane między urządzeniami.

sharded_watch_matrix = shard(watch_matrix)

Przed piszemy nasz run , niech szybko omówić dodatkowe wyzwania z sharding lokalną zmienną losową \(U\). Uruchamiając HMC wanilii tfp.mcmc.HamiltonianMonteCarlo jądro próbki pędu dla każdego elementu stanu tej sieci. Wcześniej tylko zmienne losowe bez fragmentów były częścią tego stanu, a pęd był taki sam na każdym urządzeniu. Kiedy mamy teraz sharded \(U\), musimy spróbować różne momenty na każdym urządzeniu do \(U\), podczas pobierania próbek tego samego pędu dla \(V\). Aby to osiągnąć, możemy użyć tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo z Sharded rozkładu pędu. Ponieważ kontynuujemy wykonywanie obliczeń równoległych na najwyższym poziomie, możemy to uprościć, np. przenosząc wskaźnik shardedness do jądra konsoli HMC.

def make_run(*,
             axis_name,
             dim=20,
             num_chains=2,
             prior_variance=1.,
             step_size=1e-2,
             num_leapfrog_steps=100,
             num_burnin_steps=1000,
             num_results=500,
             ):
  @functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
  @jax.default_matmul_precision('tensorfloat32')
  def run(key, watch_matrix):
    num_users, num_movies = watch_matrix.shape

    Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)

    def prior_fn():
      user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
      user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
      movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
      movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
      return (user_embeddings, user_bias, movie_embeddings, movie_bias)
    prior = tfed.JointDistributionCoroutine(prior_fn)

    def model_fn():
      user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
      logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
                + user_bias[..., :, None] + movie_bias[..., None, :])
      yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
    model = tfed.JointDistributionCoroutine(model_fn)

    init_key, sample_key = random.split(key)
    initial_state = prior.sample(seed=init_key, sample_shape=num_chains)

    def target_log_prob(*state):
      return model.log_prob((*state, watch_matrix))

    momentum_distribution = tfed.JointDistributionSequential([
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
      Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
      tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
    ])

    # We pass in momentum_distribution here to ensure that the momenta for 
    # user_embeddings and user_bias are also sharded
    kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
                                                      num_leapfrog_steps,
                                                      momentum_distribution=momentum_distribution)

    num_adaptation_steps = int(0.8 * num_burnin_steps)
    kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)

    def trace_fn(state, pkr):
      return {
        'log_prob': target_log_prob(*state),
        'log_accept_ratio': pkr.inner_results.log_accept_ratio,
      }
    return tfm.sample_chain(
        num_results, initial_state,
        kernel=kernel,
        num_burnin_steps=num_burnin_steps,
        trace_fn=trace_fn,
        seed=sample_key)
  return run

Będziemy ponownie uruchomić go raz, aby buforować skompilowany run .

%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), output)

CPU times: user 56 s, sys: 1min 24s, total: 2min 20s
Wall time: 3min 35s

Teraz uruchomimy go ponownie bez narzutu na kompilację.

%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree_map(lambda x: x.block_until_ready(), trace)

CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s
Wall time: 3min 1s

Wygląda na to, że wykonaliśmy około 150 000 przeskoków w około 3 minuty, czyli około 83 przeskoków na sekundę! Wykreślmy współczynnik akceptacji i gęstość logarytmiczną naszych próbek.

fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
  ax.plot(val[0]) # Indexing into a sharded array, each element is the same
  ax.set_title(key);

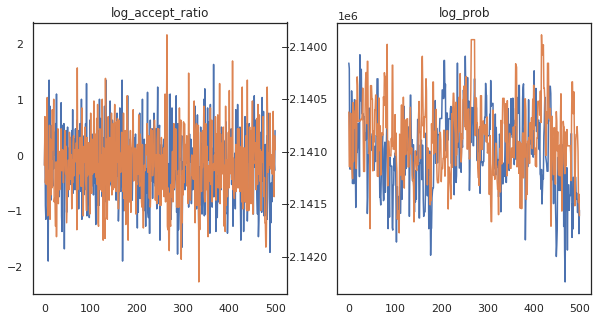
Teraz, gdy mamy kilka próbek z naszego łańcucha Markowa, wykorzystajmy je do prognozowania. Najpierw wyodrębnijmy każdy ze składników. Pamiętaj, że user_embeddings i user_bias są podzielone w poprzek urządzenia, więc musimy złączyć nasze ShardedArray je wszystkie zdobyć. Z drugiej strony, movie_embeddings i movie_bias są takie same na każdym urządzeniu, więc możemy po prostu wybrać wartość z pierwszego odłamek. Użyjemy regularne numpy skopiować wartości z tyłu TPU do CPU.

user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')

User embeddings: (500, 2, 6040, 20)
User bias: (500, 2, 6040)
Movie embeddings: (500, 2, 3706, 20)
Movie bias: (500, 2, 3706)

Spróbujmy zbudować prosty system rekomendacji, który wykorzystuje niepewność uchwyconą w tych próbkach. Napiszmy najpierw funkcję, która klasyfikuje filmy według prawdopodobieństwa oglądania.

@jax.jit
def recommend(sample, user_id):
  user_embeddings, user_bias, movie_embeddings, movie_bias = sample
  movie_logits = (
      jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
      + user_bias[user_id] + movie_bias)
  return movie_logits.argsort()[::-1]

Możemy teraz napisać funkcję, która zapętli wszystkie próbki i dla każdego z nich wybierze najwyżej oceniany film, którego użytkownik jeszcze nie oglądał. Możemy wtedy zobaczyć liczbę wszystkich polecanych filmów w próbkach.

def get_recommendations(user_id): 
  movie_ids = []
  already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
  for i in range(500):
    for j in range(2):
      sample = jax.tree_map(lambda x: x[i, j], samples)
      ranking = recommend(sample, user_id)
      for movie_id in ranking:
        if int(movie_id) not in already_watched:
          movie_ids.append(movie_id)
          break
  return movie_ids

def plot_recommendations(movie_ids, ax=None):
  titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
  ax = ax or plt.gca()
  names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
  ax.bar(names, counts)
  ax.set_xticklabels(names, rotation=90)

Weźmy użytkownika, który widział najwięcej filmów, w porównaniu z tym, który widział najmniej.

user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])

2314 20

Mamy nadzieję, że nasz system ma większą pewność co user_most niż user_least , biorąc pod uwagę, że mamy więcej informacji o jakiego rodzaju filmy user_most jest bardziej prawdopodobne, aby obejrzeć.

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');

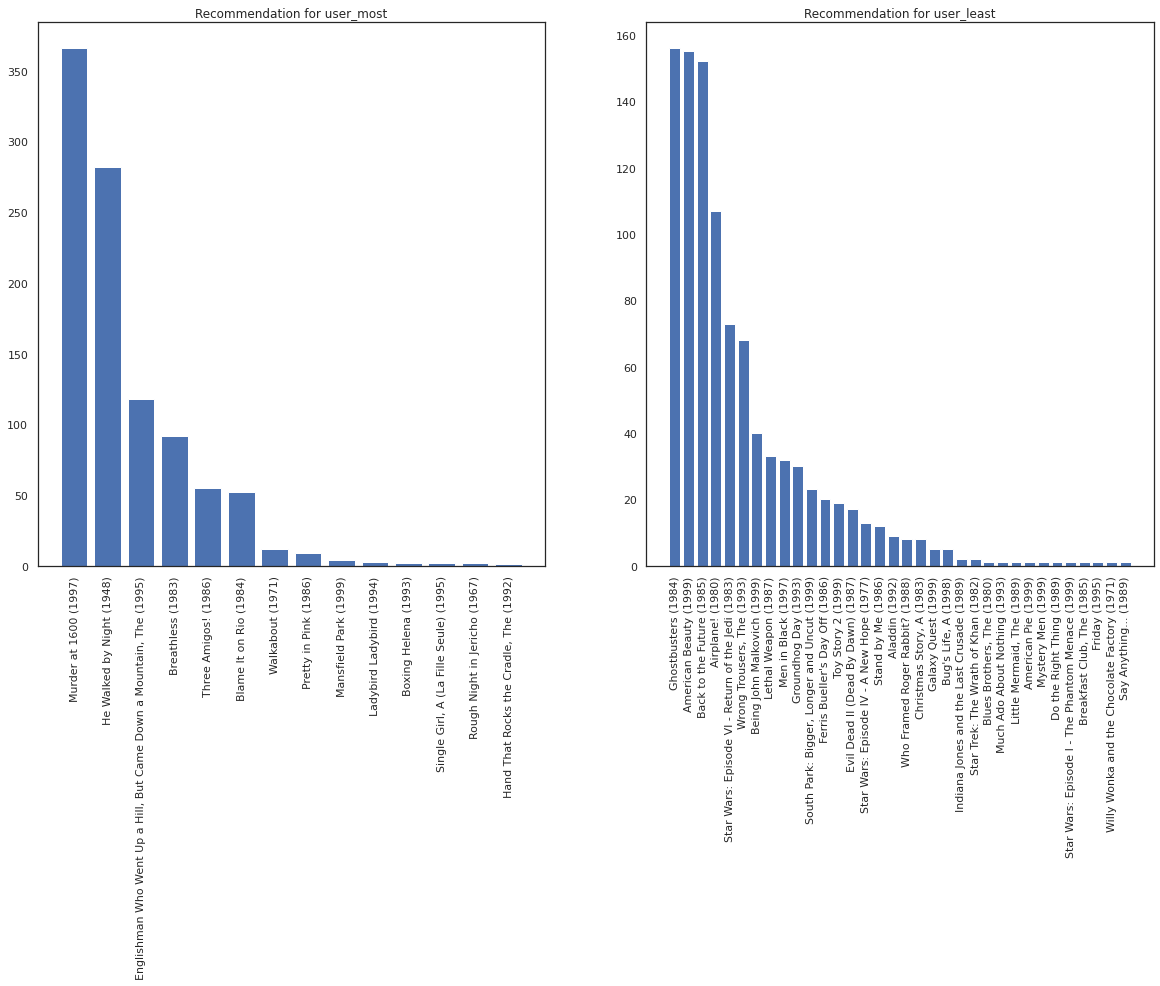
Widzimy, że istnieje więcej wariancji w naszych zaleceniach dla user_least odzwierciedla naszą dodatkową niepewność w ich preferencji zegarka.

Możemy też przyjrzeć się gatunkom polecanych filmów.

most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');

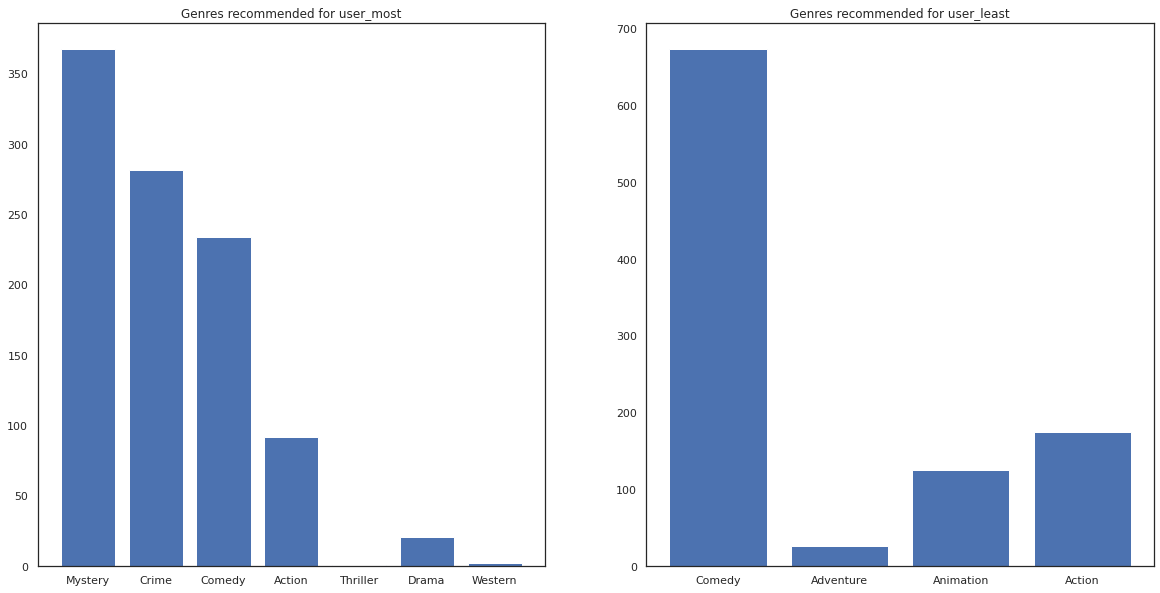
user_most widział dużo filmów i został rekomendowany więcej niszowe gatunki jak tajemnicy i przestępczością natomiast user_least nie oglądałem dużo filmów i zalecono więcej filmów głównego nurtu, co pochylać komedia i akcja.