 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
O problema oito escolas ( Rubin 1981 ) considera a eficácia de programas de treinamento SAT realizados em paralelo em oito escolas. Tornou-se um problema clássico ( Análise de Dados Bayesiana , Stan ) que ilustra a utilidade da modelagem hierárquica para a partilha de informações entre grupos permutáveis.
A IMPLEMENTAÇÃO abaixo é uma adaptação de uma 1,0 Edward tutorial .
Importações
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
import warnings
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
Os dados
Da Análise de Dados Bayesiana, seção 5.5 (Gelman et al. 2013):
Um estudo foi realizado para o serviço de teste educacional para analisar os efeitos dos programas de treinamento especial para SAT-V (Scholastic Aptitude Test-Verbal) em cada uma das oito escolas de ensino médio. A variável de resultado em cada estudo foi a pontuação em uma aplicação especial do SAT-V, um teste padronizado de múltipla escolha administrado pelo Educational Testing Service e usado para ajudar as faculdades a tomarem decisões de admissão; as pontuações podem variar entre 200 e 800, com média em torno de 500 e desvio padrão em torno de 100. Os exames SAT são projetados para resistir a esforços de curto prazo direcionados especificamente para melhorar o desempenho no teste; em vez disso, eles são projetados para refletir o conhecimento adquirido e as habilidades desenvolvidas ao longo de muitos anos de educação. No entanto, cada uma das oito escolas neste estudo considerou seu programa de coaching de curto prazo muito bem-sucedido em aumentar as pontuações do SAT. Além disso, não havia nenhuma razão anterior para acreditar que qualquer um dos oito programas fosse mais eficaz do que qualquer outro ou que alguns tivessem efeitos mais semelhantes entre si do que qualquer outro.
Para cada uma das oito escolas (\(J = 8\)), temos um efeito de tratamento estimado \(y_j\) e um erro padrão do efeito estimativa \(\sigma_j\). Os efeitos do tratamento no estudo foram obtidos por uma regressão linear no grupo de tratamento usando os escores PSAT-M e PSAT-V como variáveis de controle. Como não havia nenhuma crença anterior de que qualquer uma das escolas eram mais ou menos semelhante, ou que qualquer um dos programas de treinamento seria mais eficaz, podemos considerar os efeitos do tratamento como permutáveis .
num_schools = 8 # number of schools
treatment_effects = np.array(
[28, 8, -3, 7, -1, 1, 18, 12], dtype=np.float32) # treatment effects
treatment_stddevs = np.array(
[15, 10, 16, 11, 9, 11, 10, 18], dtype=np.float32) # treatment SE
fig, ax = plt.subplots()
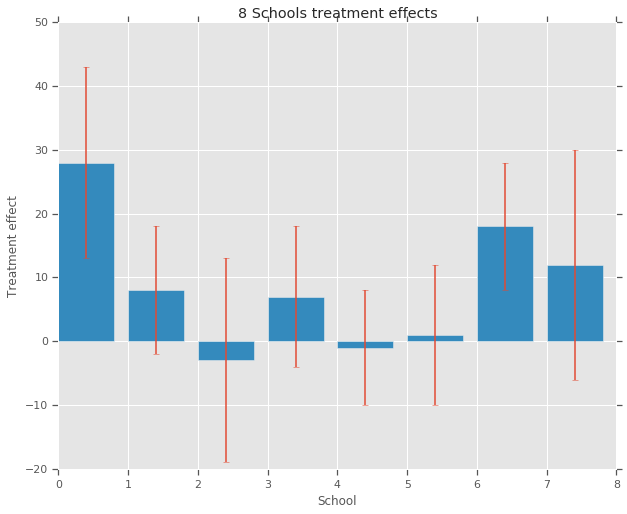
plt.bar(range(num_schools), treatment_effects, yerr=treatment_stddevs)
plt.title("8 Schools treatment effects")
plt.xlabel("School")
plt.ylabel("Treatment effect")
fig.set_size_inches(10, 8)
plt.show()
Modelo
Para capturar os dados, usamos um modelo normal hierárquico. Segue o processo gerador,
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i \sim \text{Normal}\left(\text{loc}{=}\mu,\ \text{scale}{=}\tau \right) \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
onde \(\mu\) representa o efeito médio do tratamento e anteriores \(\tau\) controla a quantidade de variância existe entre as escolas. O \(y_i\) e \(\sigma_i\) são observados. Como \(\tau \rightarrow \infty\), o modelo se aproxima do modelo não-agrupamento, ou seja, cada uma das estimativas do efeito de tratamento escola são autorizados a ser mais independente. Como \(\tau \rightarrow 0\), o modelo se aproxima do modelo completo de pooling, ou seja, todos os efeitos do tratamento da escola estão mais próximos do grupo média \(\mu\). Para restringir o desvio-padrão para ser positivo, chamamos \(\tau\) a partir de uma distribuição log-normal (que é equivalente ao desenho \(log(\tau)\) de uma distribuição normal).
Seguindo Diagnóstico inclinada inferência com Divergências , podemos transformar o modelo acima em um modelo não-centrado equivalente:
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i' \sim \text{Normal}\left(\text{loc}{=}0,\ \text{scale}{=}1 \right) \\ & \theta_i = \mu + \tau \theta_i' \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
Nós reificam este modelo como um JointDistributionSequential exemplo:
model = tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=10., name="avg_effect"), # `mu` above
tfd.Normal(loc=5., scale=1., name="avg_stddev"), # `log(tau)` above
tfd.Independent(tfd.Normal(loc=tf.zeros(num_schools),
scale=tf.ones(num_schools),
name="school_effects_standard"), # `theta_prime`
reinterpreted_batch_ndims=1),
lambda school_effects_standard, avg_stddev, avg_effect: (
tfd.Independent(tfd.Normal(loc=(avg_effect[..., tf.newaxis] +
tf.exp(avg_stddev[..., tf.newaxis]) *
school_effects_standard), # `theta` above
scale=treatment_stddevs),
name="treatment_effects", # `y` above
reinterpreted_batch_ndims=1))
])
def target_log_prob_fn(avg_effect, avg_stddev, school_effects_standard):
"""Unnormalized target density as a function of states."""
return model.log_prob((
avg_effect, avg_stddev, school_effects_standard, treatment_effects))
Inferência Bayesiana
Dados dados, realizamos Monte Carlo Hamiltoniano (HMC) para calcular a distribuição posterior sobre os parâmetros do modelo.
num_results = 5000
num_burnin_steps = 3000
# Improve performance by tracing the sampler using `tf.function`
# and compiling it using XLA.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
tf.zeros([], name='init_avg_effect'),
tf.zeros([], name='init_avg_stddev'),
tf.ones([num_schools], name='init_school_effects_standard'),
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.4,
num_leapfrog_steps=3))
states, kernel_results = do_sampling()
avg_effect, avg_stddev, school_effects_standard = states
school_effects_samples = (
avg_effect[:, np.newaxis] +
np.exp(avg_stddev)[:, np.newaxis] * school_effects_standard)
num_accepted = np.sum(kernel_results.is_accepted)
print('Acceptance rate: {}'.format(num_accepted / num_results))
Acceptance rate: 0.5974
fig, axes = plt.subplots(8, 2, sharex='col', sharey='col')
fig.set_size_inches(12, 10)
for i in range(num_schools):
axes[i][0].plot(school_effects_samples[:,i].numpy())
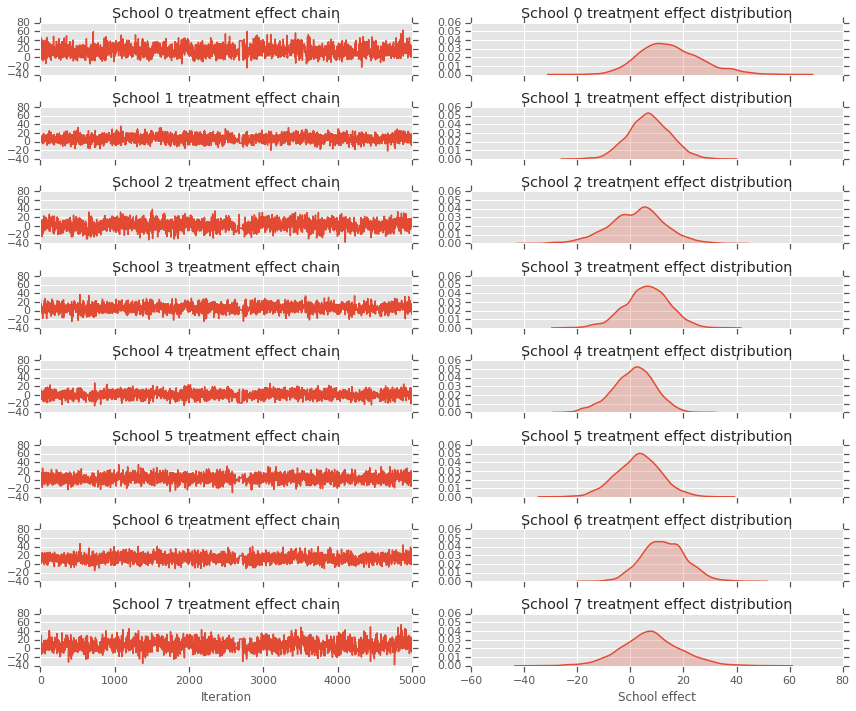
axes[i][0].title.set_text("School {} treatment effect chain".format(i))
sns.kdeplot(school_effects_samples[:,i].numpy(), ax=axes[i][1], shade=True)
axes[i][1].title.set_text("School {} treatment effect distribution".format(i))
axes[num_schools - 1][0].set_xlabel("Iteration")
axes[num_schools - 1][1].set_xlabel("School effect")
fig.tight_layout()
plt.show()
print("E[avg_effect] = {}".format(np.mean(avg_effect)))
print("E[avg_stddev] = {}".format(np.mean(avg_stddev)))
print("E[school_effects_standard] =")
print(np.mean(school_effects_standard[:, ]))
print("E[school_effects] =")
print(np.mean(school_effects_samples[:, ], axis=0))
E[avg_effect] = 5.57183933258 E[avg_stddev] = 2.47738981247 E[school_effects_standard] = 0.08509017 E[school_effects] = [15.0051 7.103311 2.4552586 6.2744603 1.3364682 3.1125953 12.762501 7.743602 ]
# Compute the 95% interval for school_effects
school_effects_low = np.array([
np.percentile(school_effects_samples[:, i], 2.5) for i in range(num_schools)
])
school_effects_med = np.array([
np.percentile(school_effects_samples[:, i], 50) for i in range(num_schools)
])
school_effects_hi = np.array([
np.percentile(school_effects_samples[:, i], 97.5)
for i in range(num_schools)
])
fig, ax = plt.subplots(nrows=1, ncols=1, sharex=True)
ax.scatter(np.array(range(num_schools)), school_effects_med, color='red', s=60)
ax.scatter(
np.array(range(num_schools)) + 0.1, treatment_effects, color='blue', s=60)
plt.plot([-0.2, 7.4], [np.mean(avg_effect),
np.mean(avg_effect)], 'k', linestyle='--')
ax.errorbar(
np.array(range(8)),
school_effects_med,
yerr=[
school_effects_med - school_effects_low,
school_effects_hi - school_effects_med
],
fmt='none')
ax.legend(('avg_effect', 'HMC', 'Observed effect'), fontsize=14)
plt.xlabel('School')
plt.ylabel('Treatment effect')
plt.title('HMC estimated school treatment effects vs. observed data')
fig.set_size_inches(10, 8)
plt.show()
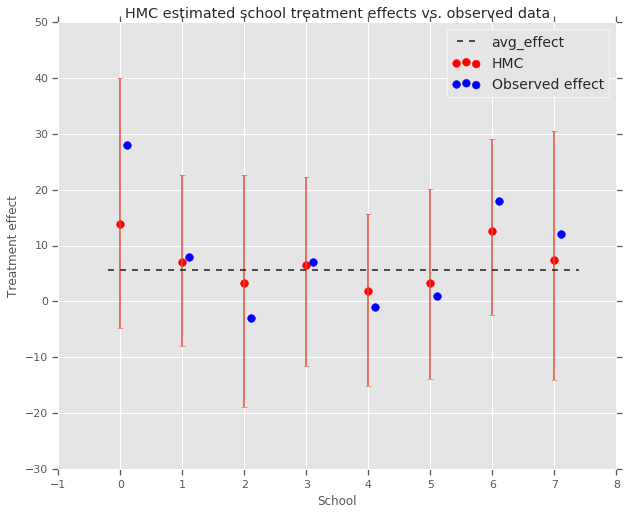
Podemos observar o encolhimento em direção ao grupo avg_effect acima.
print("Inferred posterior mean: {0:.2f}".format(
np.mean(school_effects_samples[:,])))
print("Inferred posterior mean se: {0:.2f}".format(
np.std(school_effects_samples[:,])))
Inferred posterior mean: 6.97 Inferred posterior mean se: 10.41
Crítica
Para obter a distribuição preditiva posterior, ou seja, um modelo de novos dados \(y^*\) dado os dados observados \(y\):
\[ p(y^*|y) \propto \int_\theta p(y^* | \theta)p(\theta |y)d\theta\]
que substituem os valores das variáveis aleatórias no modelo para defini-los para a média da distribuição posterior, e a amostra a partir desse modelo para gerar novos dados \(y^*\).
sample_shape = [5000]
_, _, _, predictive_treatment_effects = model.sample(
value=(tf.broadcast_to(np.mean(avg_effect, 0), sample_shape),
tf.broadcast_to(np.mean(avg_stddev, 0), sample_shape),
tf.broadcast_to(np.mean(school_effects_standard, 0),
sample_shape + [num_schools]),
None))
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(predictive_treatment_effects[:, 2*i].numpy(),
ax=ax[0], shade=True)
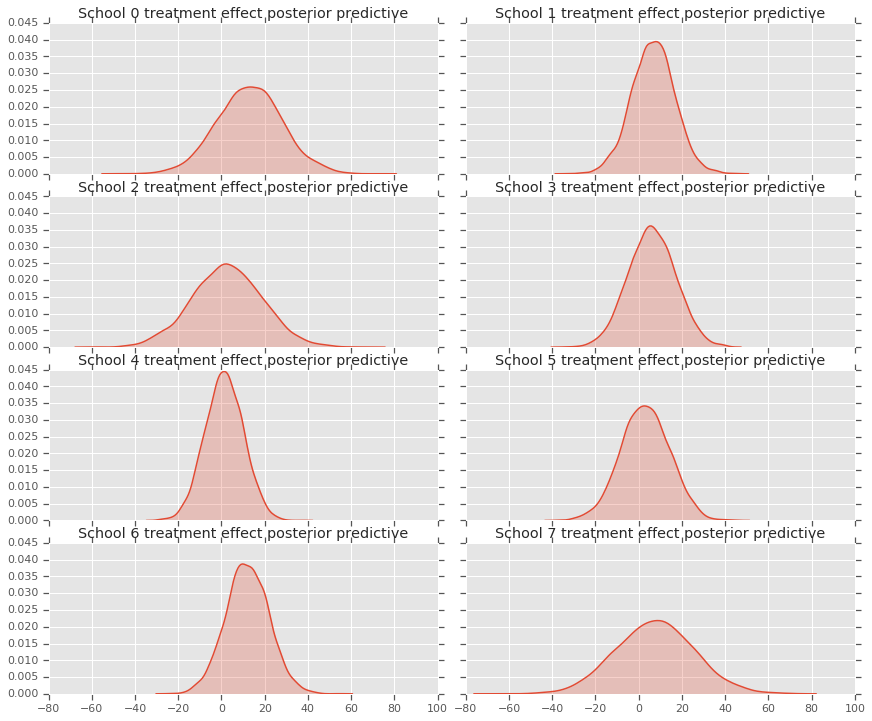
ax[0].title.set_text(
"School {} treatment effect posterior predictive".format(2*i))
sns.kdeplot(predictive_treatment_effects[:, 2*i + 1].numpy(),
ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect posterior predictive".format(2*i + 1))
plt.show()
# The mean predicted treatment effects for each of the eight schools.
prediction = np.mean(predictive_treatment_effects, axis=0)
Podemos olhar para os resíduos entre os dados dos efeitos do tratamento e as previsões do modelo posterior. Estes correspondem ao gráfico acima, que mostra a redução dos efeitos estimados em relação à média da população.
treatment_effects - prediction
array([14.905351 , 1.2838383, -5.6966295, 0.8327627, -2.3356671,
-2.0363257, 5.997898 , 4.3731265], dtype=float32)
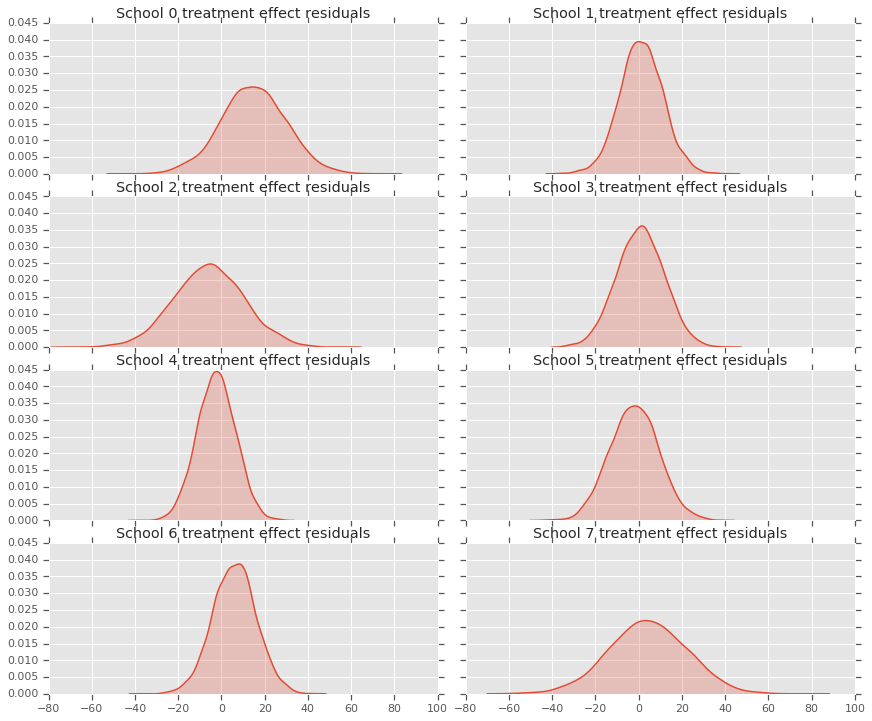
Como temos uma distribuição de previsões para cada escola, podemos considerar a distribuição de resíduos também.
residuals = treatment_effects - predictive_treatment_effects
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(residuals[:, 2*i].numpy(), ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect residuals".format(2*i))
sns.kdeplot(residuals[:, 2*i + 1].numpy(), ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect residuals".format(2*i + 1))
plt.show()
Reconhecimentos
Este tutorial foi escrito originalmente em Edward 1,0 ( fonte ). Agradecemos a todos os colaboradores por escrever e revisar essa versão.
Referências
- Donald B. Rubin. Estimativa em experimentos paralelos randomizados. Journal of Educational Statistics, 6 (4): 377-401, 1981.
- Andrew Gelman, John Carlin, Hal Stern, David Dunson, Aki Vehtari e Donald Rubin. Análise de dados bayesiana, terceira edição. Chapman e Hall / CRC, 2013.
