 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Um [cópula] (https://en.wikipedia.org/wiki/Copula_ (probability_theory% 29) é uma abordagem clássica para capturar a dependência entre variáveis aleatórias. Mais formalmente, uma cópula é uma distribuição multivariada \(C(U_1, U_2, ...., U_n)\) tal que marginalizador dá \(U_i \sim \text{Uniform}(0, 1)\).
Cópulas são interessantes porque podemos usá-los para criar distribuições multivariadas com marginais arbitrárias. Esta é a receita:
- Usando o integral de probabilidade Transform voltas um RV contínua arbitrária \(X\) num uniforme uma \(F_X(X)\), onde \(F_X\) é a CDF de \(X\).
- Dada uma cópula (digamos bivariada) \(C(U, V)\), temos que \(U\) e \(V\) têm distribuições marginais uniformes.
- Agora dado o nosso RV é de interesse \(X, Y\), criar uma distribuição nova \(C'(X, Y) = C(F_X(X), F_Y(Y))\). Os marginais para \(X\) e \(Y\) são os que nós desejados.
Os marginais são univariados e, portanto, podem ser mais fáceis de medir e / ou modelar. Uma cópula permite começar a partir dos marginais, mas também alcançar uma correlação arbitrária entre as dimensões.
Cópula Gaussiana
Para ilustrar como as cópulas são construídas, considere o caso de captura de dependência de acordo com correlações gaussianas multivariadas. Um Gaussiana Copula é um dado por \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) onde \(\Phi_\Sigma\) representa a CDF de um MultivariateNormal, com covariância \(\Sigma\) e média 0, e \(\Phi^{-1}\) é o CDF inversa para o padrão normal.
Aplicar o CDF inverso do normal distorce as dimensões uniformes para serem normalmente distribuídas. Aplicar o CDF da normal multivariada então comprime a distribuição para ser marginalmente uniforme e com correlações gaussianas.
Assim, o que temos é que o Gaussian Cópula é uma distribuição sobre a unidade hypercube \([0, 1]^n\) com os marginais uniformes.
Definido como tal, o Gaussian Cópula pode ser implementado com tfd.TransformedDistribution e apropriada Bijector . Ou seja, estamos transformando uma MultivariateNormal, através do uso da distribuição normal do inverso CDF, implementado pelo tfb.NormalCDF bijector.
A seguir, implementar uma Gaussiana Copula com um pressuposto simplificando: que a covariância é parametrizada por um factor de Cholesky (daí uma covariância para MultivariateNormalTriL ). (Pode-se usar outras tf.linalg.LinearOperators para codificar diferentes hipóteses livre de matriz.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
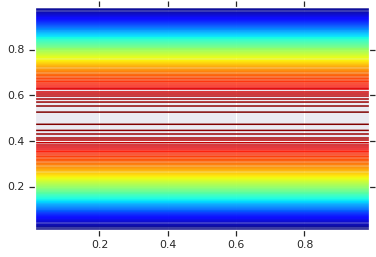
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
O poder, entretanto, de tal modelo é usar a Transformada Integral de Probabilidade, para usar a cópula em RVs arbitrários. Dessa forma, podemos especificar marginais arbitrários e usar a cópula para costurá-los.
Começamos com um modelo:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
e usar a cópula para obter um RV bivariada \(Z\), que tem marginais Kumaraswamy e Gumbel .
Começaremos traçando a distribuição do produto gerado por esses dois RVs. Isso serve apenas como um ponto de comparação para quando aplicamos o Copula.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
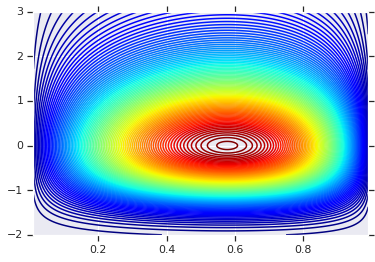
Distribuição Conjunta com Diferentes Marginais
Agora usamos uma cópula gaussiana para acoplar as distribuições e plotar isso. Mais uma vez a nossa ferramenta de escolha é TransformedDistribution aplicar o apropriado Bijector para obter os marginais escolhidos.
Especificamente, usamos um Blockwise bijector que aplica diferentes bijectors em diferentes partes do vector (que é ainda uma transformação bijective).
Agora podemos definir o Copula que queremos. Dada uma lista de marginais alvo (codificados como bijetores), podemos facilmente construir uma nova distribuição que usa a cópula e tem os marginais especificados.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
Finalmente, vamos realmente usar esta cópula gaussiana. Vamos utilizar um Cholesky de \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\), o que vai corresponder a desvios de 1, e correlação \(\rho\) para o normal multivariada.
Veremos alguns casos:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
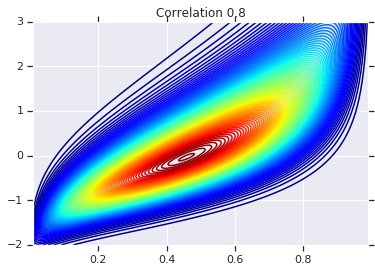
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
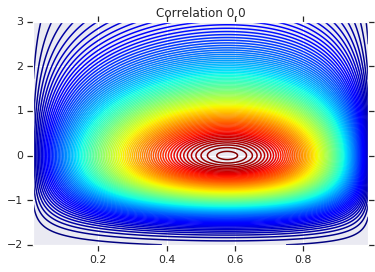
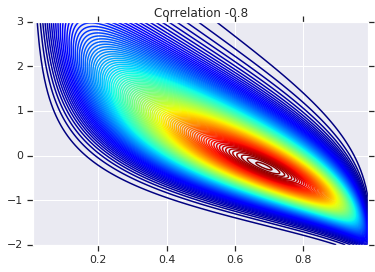
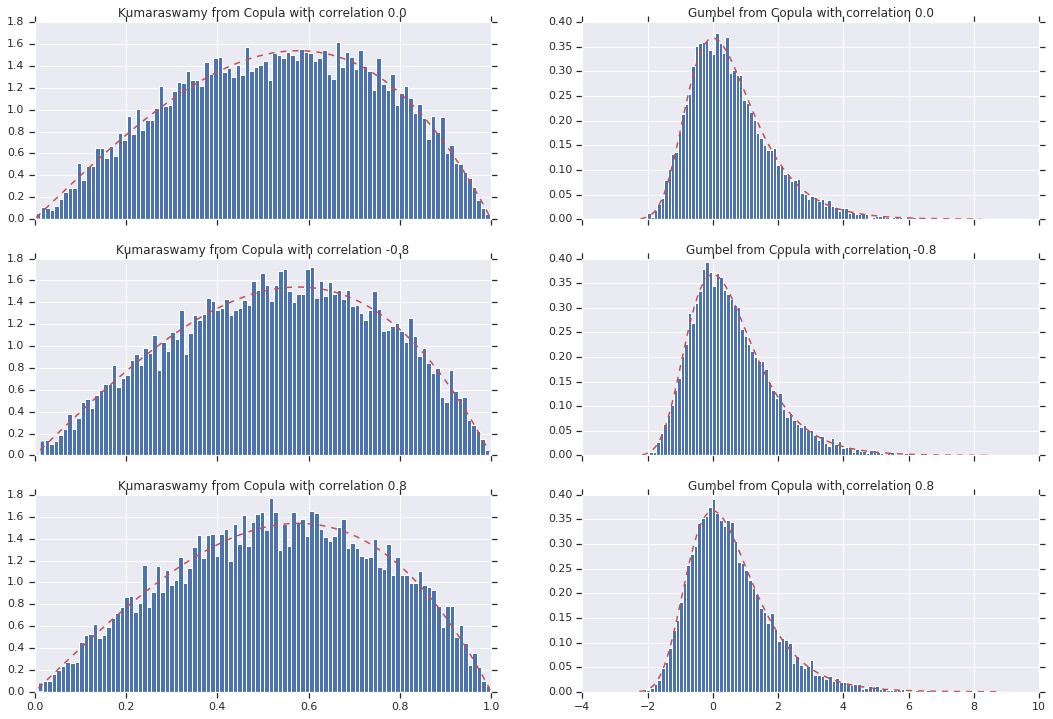
Finalmente, vamos verificar se realmente obtemos os marginais que queremos.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
Conclusão
E lá vamos nós! Nós demonstramos que podemos construir Gaussian cópulas usando o Bijector API.
De modo mais geral, escrevendo bijectors usando o Bijector API e compõem-los com uma distribuição, pode criar famílias ricas de distribuições para a modelagem flexível.
