 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Um modelo linear de efeitos mistos é uma abordagem simples para modelar relacionamentos lineares estruturados (Harville, 1997; Laird e Ware, 1982). Cada ponto de dados consiste em entradas de vários tipos - categorizadas em grupos - e uma saída com valor real. Um modelo linear de efeitos mistos é um modelo hierárquico: partilha força estatística entre os grupos, a fim de melhorar inferências sobre qualquer ponto de dados individual.
Neste tutorial, demonstramos modelos lineares de efeitos mistos com um exemplo do mundo real na Probabilidade do TensorFlow. Usaremos o JointDistributionCoroutine e Markov Chain Monte Carlo ( tfp.mcmc ) módulos.
Dependências e pré-requisitos
Importar e configurar
import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')
Torne as coisas mais rápidas!
Antes de começarmos, vamos ter certeza de que estamos usando uma GPU para esta demonstração.
Para fazer isso, selecione "Runtime" -> "Alterar tipo de tempo de execução" -> "Acelerador de hardware" -> "GPU".
O snippet a seguir verificará se temos acesso a uma GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
Dados
Usamos as InstEval definidas a partir do popular dados lme4 pacote em R (Bates et al., 2015). É um conjunto de dados de cursos e suas classificações de avaliação. Cada curso inclui metadados, como students , instructors e departments , e a variável resposta de interesse é a classificação de avaliação.
def load_insteval():
"""Loads the InstEval data set.
It contains 73,421 university lecture evaluations by students at ETH
Zurich with a total of 2,972 students, 2,160 professors and
lecturers, and several student, lecture, and lecturer attributes.
Implementation is built from the `observations` Python package.
Returns:
Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
dictionary `metadata` of column headers (feature names).
"""
url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
'lme4/InstEval.csv')
with requests.Session() as s:
download = s.get(url)
f = download.content.decode().splitlines()
iterator = csv.reader(f)
columns = next(iterator)[1:]
x_train = np.array([row[1:] for row in iterator], dtype=np.int)
metadata = {'columns': columns}
return x_train, metadata
Carregamos e pré-processamos o conjunto de dados. Retemos 20% dos dados para que possamos avaliar nosso modelo ajustado em pontos de dados invisíveis. Abaixo, visualizamos as primeiras linhas.
data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
'd': 'instructors',
'dept': 'departments',
'y': 'ratings'})
data['students'] -= 1 # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes
train = data.sample(frac=0.8)
test = data.drop(train.index)
train.head()
Montamos o conjunto de dados em termos de features dicionário de entradas e labels de saída correspondente às classificações. Cada recurso é codificado como um inteiro e cada rótulo (classificação de avaliação) é codificado como um número de ponto flutuante.
get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
k: get_value(train, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)
features_test = {k: get_value(test, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)
num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]
print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)
Number of students: 2972 Number of instructors: 1128 Number of departments: 14 Number of observations: 58737
Modelo
Um modelo linear típico assume independência, onde qualquer par de pontos de dados tem um relacionamento linear constante. No InstEval conjunto de dados, observações surgem em grupos, cada um dos quais pode ter diferentes pistas e intercepta. Modelos lineares de efeitos mistos, também conhecidos como modelos lineares hierárquicos ou modelos lineares multiníveis, capturam esse fenômeno (Gelman & Hill, 2006).
Exemplos desse fenômeno incluem:
- Alunos. As observações de um aluno não são independentes: alguns alunos podem sistematicamente dar notas baixas (ou altas) nas aulas.
- Instrutores. As observações de um instrutor não são independentes: esperamos que bons professores geralmente tenham boas avaliações e que professores ruins geralmente tenham avaliações ruins.
- Departamentos. As observações de um departamento não são independentes: certos departamentos podem geralmente ter material seco ou classificação mais rígida e, portanto, ser avaliados abaixo de outros.
Para capturar isso, lembre-se que para um conjunto de dados de \(N\times D\) apresenta \(\mathbf{X}\) e \(N\) etiquetas \(\mathbf{y}\), postula de regressão linear do modelo
\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]
onde há uma inclinação vector \(\beta\in\mathbb{R}^D\), interceptar \(\alpha\in\mathbb{R}\)e ruído aleatório \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Dizemos que \(\beta\) e \(\alpha\) são "efeitos fixos": são efeitos mantidas constantes em toda a população de pontos de dados \((x, y)\). Uma formulação equivalente da equação como uma probabilidade é \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\). Esta probabilidade é maximizada durante a inferência, a fim de encontrar as estimativas pontuais de \(\beta\) e \(\alpha\) que se encaixam os dados.
Um modelo de efeitos mistos lineares estende a regressão linear como
\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]
onde ainda há uma inclinação vector \(\beta\in\mathbb{R}^P\), interceptar \(\alpha\in\mathbb{R}\)e ruído aleatório \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Além disso, existe um termo \(\mathbf{Z}\eta\), onde \(\mathbf{Z}\) é uma matriz de características e \(\eta\in\mathbb{R}^Q\) é um vector de pistas aleatórias; \(\eta\) é normalmente distribuída com parâmetro de componentes de variância \(\sigma^2\). \(\mathbf{Z}\) é formado por particionar o original \(N\times D\) possui matriz em termos de uma nova \(N\times P\) matriz \(\mathbf{X}\) e \(N\times Q\) matriz \(\mathbf{Z}\), onde \(P + Q=D\): esta partição nos permite modelar as características separadamente usando os efeitos fixos \(\beta\) e a variável latente \(\eta\) respectivamente.
Dizemos as variáveis latentes \(\eta\) são "efeitos aleatórios": são efeitos que variam toda a população (embora possam ser constante em subpopulações). Em particular, porque os efeitos aleatórios \(\eta\) tem média 0, médio do rótulo de dados é capturado por \(\mathbf{X}\beta + \alpha\). Os efeitos aleatórios componentes \(\mathbf{Z}\eta\) capta as variações dos dados: por exemplo, "instrutor # 54 é classificado 1,4 pontos mais elevados do que a média."
Neste tutorial, postulamos os seguintes efeitos:
- Efeitos fixos:
service.serviceé uma co-variável binária correspondente ao facto do curso pertence ao departamento principal do instrutor. Não importa o quanto de dados adicionais que coletamos, só pode assumir valores \(0\) e \(1\). - Efeitos aleatórios:
students,instructorsedepartments. Dadas mais observações da população de classificações de avaliação de cursos, podemos estar olhando para novos alunos, professores ou departamentos.
Na sintaxe do pacote lme4 de R (Bates et al., 2015), o modelo pode ser resumido como
ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1
onde x indica um efeito fixo, (1|x) indica um efeito aleatório para x , e 1 indica um termo intercepção.
Implementamos este modelo abaixo como uma JointDistribution. Para ter um melhor suporte para monitoramento de parâmetros (por exemplo, queremos acompanhar todo o tf.Variable em model.trainable_variables ), vamos implementar o modelo modelo como tf.Module .
class LinearMixedEffectModel(tf.Module):
def __init__(self):
# Set up fixed effects and other parameters.
# These are free parameters to be optimized in E-steps
self._intercept = tf.Variable(0., name="intercept") # alpha in eq
self._effect_service = tf.Variable(0., name="effect_service") # beta in eq
self._stddev_students = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_students") # sigma in eq
self._stddev_instructors = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_instructors") # sigma in eq
self._stddev_departments = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_departments") # sigma in eq
def __call__(self, features):
model = tfd.JointDistributionSequential([
# Set up random effects.
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_students),
scale_identity_multiplier=self._stddev_students),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_instructors),
scale_identity_multiplier=self._stddev_instructors),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_departments),
scale_identity_multiplier=self._stddev_departments),
# This is the likelihood for the observed.
lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
tfd.Normal(
loc=(self._effect_service * features["service"] +
tf.gather(effect_students, features["students"], axis=-1) +
tf.gather(effect_instructors, features["instructors"], axis=-1) +
tf.gather(effect_departments, features["departments"], axis=-1) +
self._intercept),
scale=1.),
reinterpreted_batch_ndims=1)
])
# To enable tracking of the trainable variables via the created distribution,
# we attach a reference to `self`. Since all TFP objects sub-class
# `tf.Module`, this means that the following is possible:
# LinearMixedEffectModel()(features_train).trainable_variables
# ==> tuple of all tf.Variables created by LinearMixedEffectModel.
model._to_track = self
return model
lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)
lmm_train.trainable_variables
(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)
Como um programa gráfico Probabilístico, também podemos visualizar a estrutura do modelo em termos de seu gráfico computacional. Este gráfico codifica o fluxo de dados através das variáveis aleatórias no programa, tornando explícito seus relacionamentos em termos de um modelo gráfico (Jordan, 2003).
Como uma ferramenta estatística, podemos olhar para o gráfico, a fim de ver melhor, por exemplo, que intercept e effect_service são condicionalmente dadas dependentes ratings ; isso pode ser mais difícil de ver no código-fonte se o programa for escrito com classes, referências cruzadas entre módulos e / ou sub-rotinas. Como uma ferramenta computacional, nós também pode notar variáveis latentes fluir para o ratings variável via tf.gather ops. Isso pode ser um gargalo em determinados aceleradores de hardware, se a indexação Tensor s é caro; visualizar o gráfico torna isso prontamente aparente.
lmm_train.resolve_graph()
(('effect_students', ()),
('effect_instructors', ()),
('effect_departments', ()),
('x', ('effect_departments', 'effect_instructors', 'effect_students')))
Estimativa de Parâmetro
Dado os dados, o objetivo de inferência é encaixar o modelo de efeitos fixos inclinação \(\beta\), interceptar \(\alpha\), e variância parâmetro componente \(\sigma^2\). O princípio de máxima verossimilhança formaliza esta tarefa como
\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]
Neste tutorial, usamos o algoritmo Monte Carlo EM para maximizar esta densidade marginal (Dempster et al., 1977; Wei e Tanner, 1990). Realizamos a cadeia de Markov Monte Carlo para calcular a expectativa da verossimilhança condicional em relação ao efeitos aleatórios ("E-step"), e realizamos uma descida gradiente para maximizar a expectativa em relação aos parâmetros ("M-step"):
Para a etapa E, configuramos o Hamiltoniano Monte Carlo (HMC). Ele obtém um estado atual - os efeitos do aluno, instrutor e departamento - e retorna um novo estado. Atribuímos o novo estado às variáveis do TensorFlow, que denotam o estado da cadeia HMC.
Para a etapa M, usamos a amostra posterior de HMC para calcular uma estimativa não enviesada da verossimilhança marginal até uma constante. Em seguida, aplicamos seu gradiente em relação aos parâmetros de interesse. Isso produz um degrau de descida estocástica imparcial na probabilidade marginal. Nós o implementamos com o otimizador Adam TensorFlow e minimizamos o negativo do marginal.
target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]
# For debugging
target_log_prob_fn(*current_state)
<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>
# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.015,
num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)
@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
next_state, next_kernel_results = hmc.one_step(
current_state=current_state,
previous_kernel_results=kernel_results)
return next_state, next_kernel_results
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
with tf.GradientTape() as tape:
loss = -target_log_prob_fn(*current_state)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
Realizamos um estágio de aquecimento, que executa uma cadeia MCMC por um número de iterações para que o treinamento possa ser inicializado dentro da massa de probabilidade posterior. Em seguida, executamos um loop de treinamento. Ele executa as etapas E e M em conjunto e registra os valores durante o treinamento.
num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])
# Run warm-up stage.
for t in range(num_warmup_iters):
current_state, kernel_results = one_e_step(current_state, kernel_results)
num_accepted += kernel_results.is_accepted.numpy()
if t % 500 == 0 or t == num_warmup_iters - 1:
print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
t, num_accepted / (t + 1)))
num_accepted = 0 # reset acceptance rate counter
# Run training.
for t in range(num_iters):
# run 5 MCMC iterations before every joint EM update
for _ in range(5):
current_state, kernel_results = one_e_step(current_state, kernel_results)
loss = one_m_step(current_state)
effect_students_samples[t, :] = current_state[0].numpy()
effect_instructors_samples[t, :] = current_state[1].numpy()
effect_departments_samples[t, :] = current_state[2].numpy()
num_accepted += kernel_results.is_accepted.numpy()
loss_history[t] = loss.numpy()
if t % 500 == 0 or t == num_iters - 1:
print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
t, num_accepted / (t + 1), loss_history[t]))
Warm-Up Iteration: 0 Acceptance Rate: 1.000 Warm-Up Iteration: 500 Acceptance Rate: 0.754 Warm-Up Iteration: 999 Acceptance Rate: 0.707 Iteration: 0 Acceptance Rate: 1.000 Loss: 98220.266 Iteration: 500 Acceptance Rate: 0.703 Loss: 96003.969 Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609 Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891
Você também pode escrever o aquecimento para-circuito em um tf.while_loop , ea etapa de formação em um tf.scan ou tf.while_loop para ainda mais rápido inferência. Por exemplo:
@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
_, next_state, next_kernel_results = tf.while_loop(
cond=lambda i, state, pkr: i < k,
body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
loop_vars=(tf.constant(0), current_state, kernel_results)
)
return next_state, next_kernel_results
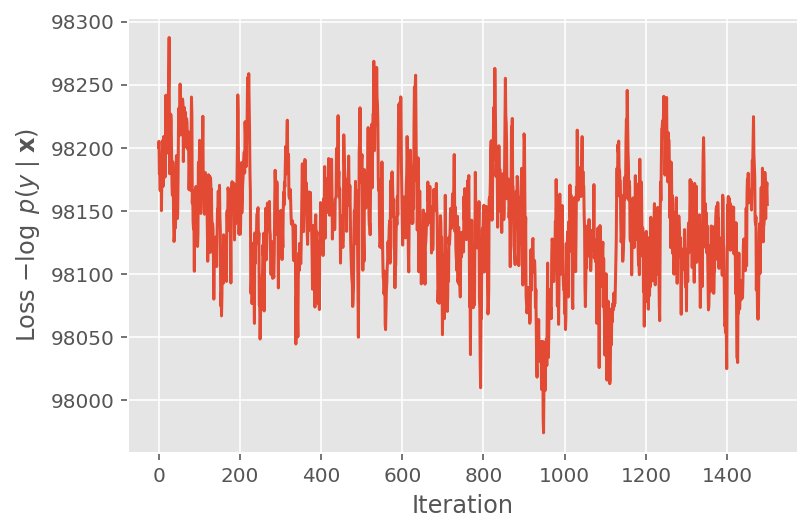
Acima, não executamos o algoritmo até que um limite de convergência fosse detectado. Para verificar se o treinamento foi sensato, verificamos que a função de perda de fato tende a convergir sobre as iterações de treinamento.
plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()
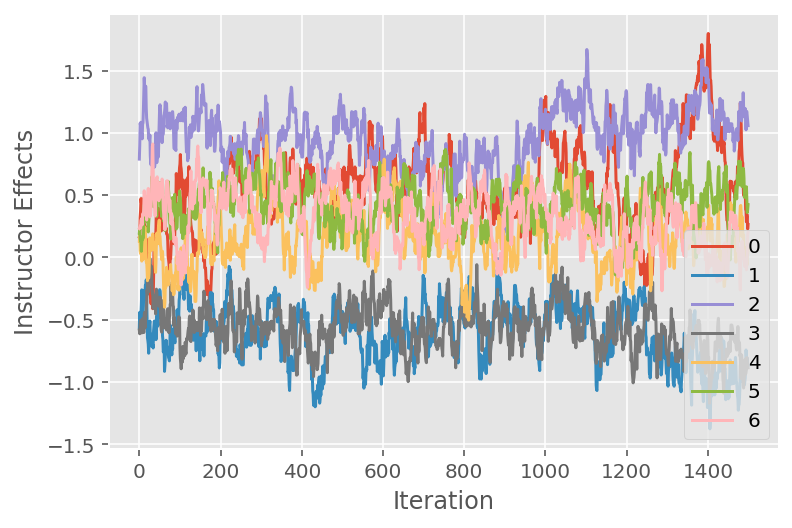
Também usamos um trace plot, que mostra a trajetória do algoritmo de Monte Carlo da cadeia de Markov em dimensões latentes específicas. Abaixo, vemos que efeitos específicos do instrutor realmente fazem uma transição significativa de seu estado inicial e exploram o espaço de estados. O traçado gráfico também indica que os efeitos diferem entre os instrutores, mas com comportamento de mistura semelhante.
for i in range(7):
plt.plot(effect_instructors_samples[:, i])
plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()
Crítica
Acima, ajustamos o modelo. Agora analisamos criticar seu ajuste usando dados, o que nos permite explorar e entender melhor o modelo. Uma dessas técnicas é um gráfico residual, que representa a diferença entre as previsões do modelo e a verdade fundamental para cada ponto de dados. Se o modelo estiver correto, então sua diferença deve ser normalmente distribuída por padrão; quaisquer desvios deste padrão no gráfico indicam desajuste do modelo.
Construímos o gráfico residual formando primeiro a distribuição preditiva posterior sobre as classificações, que substitui a distribuição anterior nos efeitos aleatórios com seus dados de treinamento dados posteriores. Em particular, executamos o modelo para a frente e interceptamos sua dependência de efeitos aleatórios anteriores com suas médias posteriores inferidas.²
lmm_test = lmm_jointdist(features_test)
[
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
] = [
np.mean(x, axis=0).astype(np.float32) for x in [
effect_students_samples,
effect_instructors_samples,
effect_departments_samples
]
]
# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
value=(
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
))
ratings_prediction = ratings_posterior.mean()
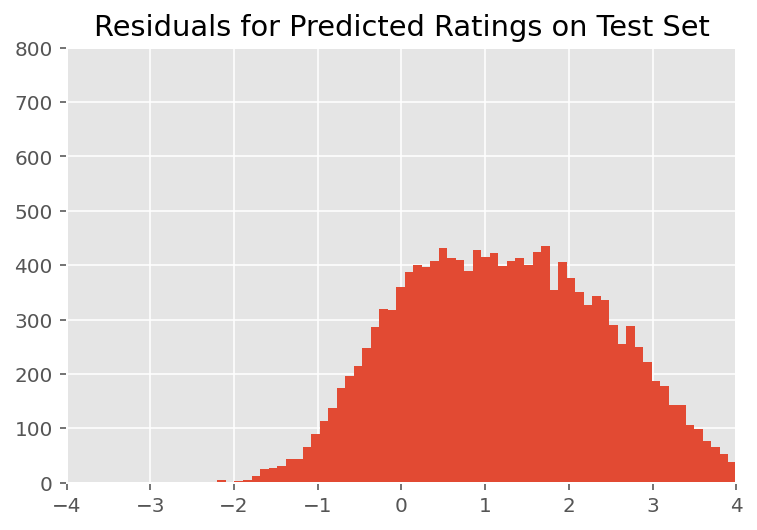
Após a inspeção visual, os resíduos parecem de alguma forma distribuídos normalmente. No entanto, o ajuste não é perfeito: há uma massa de probabilidade maior nas caudas do que uma distribuição normal, o que indica que o modelo pode melhorar seu ajuste relaxando suas suposições de normalidade.
Em particular, embora seja mais comum o uso de uma distribuição normal para avaliações modelo no InstEval conjunto de dados, um olhar mais atento dos dados revela que as notações de avaliação do curso estão em valores ordinais fato de 1 a 5. Isso sugere que devemos estar usando uma distribuição ordinal, ou mesmo Categórica, se tivermos dados suficientes para descartar a ordem relativa. Esta é uma alteração de uma linha para o modelo acima; o mesmo código de inferência é aplicável.
plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()
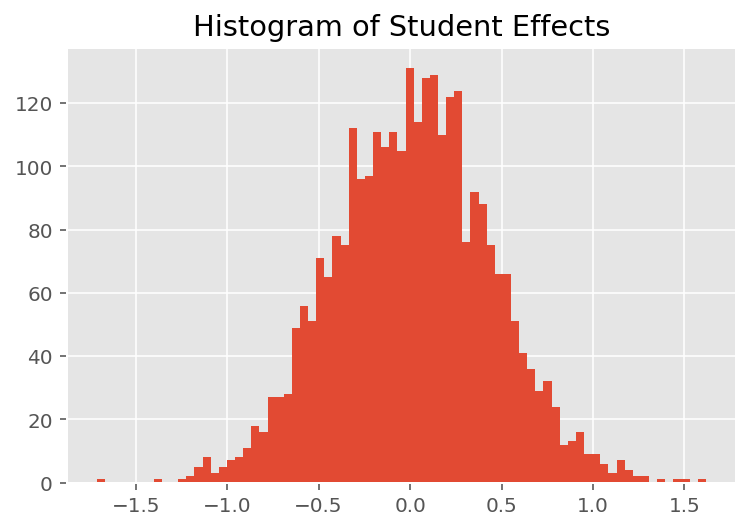
Para explorar como o modelo faz previsões individuais, examinamos o histograma de efeitos para alunos, instrutores e departamentos. Isso nos permite entender como os elementos individuais em um vetor de recursos de ponto de dados tendem a influenciar o resultado.
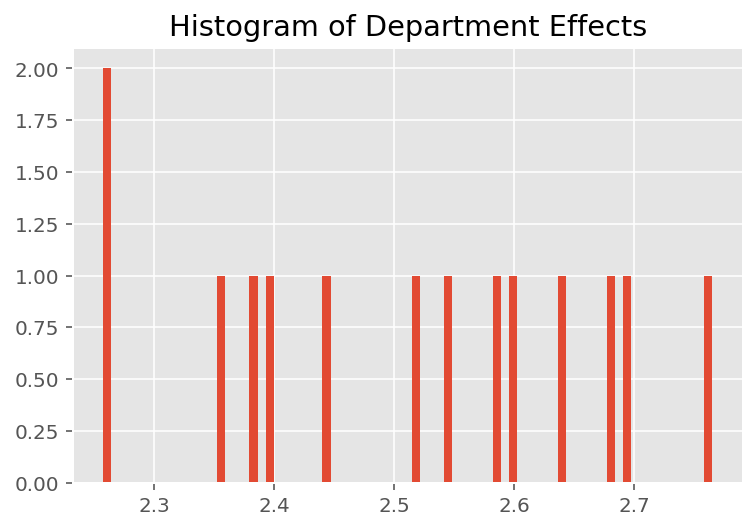
Sem surpresa, vemos abaixo que cada aluno normalmente tem pouco efeito na classificação de avaliação de um instrutor. Curiosamente, vemos que o departamento ao qual um instrutor pertence tem um grande efeito.
plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()
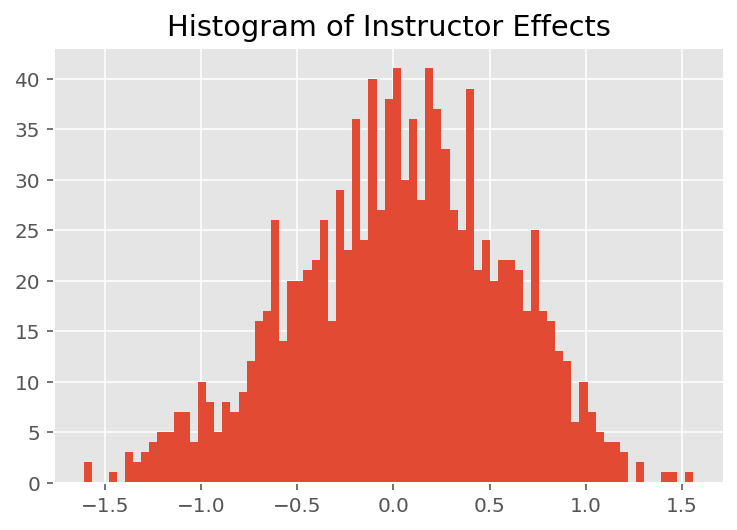
plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()
plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()
Notas de rodapé
¹ Modelos lineares de efeitos mistos são um caso especial onde podemos calcular analiticamente sua densidade marginal. Para os fins deste tutorial, demonstramos Monte Carlo EM, que se aplica mais prontamente a densidades marginais não analíticas, como se a probabilidade fosse estendida para ser Categórica em vez de Normal.
² Para simplificar, formamos a média da distribuição preditiva usando apenas uma passagem para frente do modelo. Isso é feito pelo condicionamento na média posterior e é válido para modelos lineares de efeitos mistos. No entanto, isso não é válido em geral: a média da distribuição preditiva posterior é normalmente intratável e requer a obtenção da média empírica em várias passagens para frente do modelo dadas amostras posteriores.
Agradecimentos
Este tutorial foi escrito originalmente em Edward 1,0 ( fonte ). Agradecemos a todos os colaboradores por escrever e revisar essa versão.
Referências
Douglas Bates e Martin Machler e Ben Bolker e Steve Walker. Ajustando modelos lineares de efeitos mistos usando lme4. Journal of Statistical Software, 67 (1): 1-48, 2015.
Arthur P. Dempster, Nan M. Laird e Donald B. Rubin. Máxima probabilidade de dados incompletos por meio do algoritmo EM. Journal of Royal Statistical Society, série B (metodológico), 1-38, 1977.
Andrew Gelman e Jennifer Hill. Análise de dados por meio de regressão e modelos multiníveis / hierárquicos. Cambridge University Press, 2006.
David A. Harville. Abordagens de máxima verossimilhança para estimativa do componente de variância e problemas relacionados. Journal of the American Statistical Association, 72 (358): 320-338, 1977.
Michael I. Jordan. Uma introdução aos modelos gráficos. Relatório Técnico, 2003.
Nan M. Laird e James Ware. Modelos de efeitos aleatórios para dados longitudinais. Biometrics, 963-974, 1982.
Greg Wei e Martin A. Tanner. Uma implementação de Monte Carlo do algoritmo EM e algoritmos de aumento de dados do homem pobre. Jornal da Associação Americana de Estatística, 699-704, 1990.
