 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Wnioskowanie wariacyjne (VI) rzuca przybliżone wnioskowanie bayesowskie jako problem optymalizacji i poszukuje „zastępczego” rozkładu a posteriori, który minimalizuje rozbieżność KL z prawdziwym a posteriori. Gradientowa VI jest często szybsza niż metody MCMC, składa się w naturalny sposób z optymalizacją parametrów modelu i zapewnia dolną granicę dowodów modelu, które można wykorzystać bezpośrednio do porównania modeli, diagnozy zbieżności i wnioskowania komponowanego.
TensorFlow Probability oferuje narzędzia do szybkiego, elastycznego i skalowalnego VI, które naturalnie dopasowuje się do stosu TFP. Narzędzia te umożliwiają konstruowanie zastępczych a posterioriów ze strukturami kowariancji indukowanymi przez przekształcenia liniowe lub normalizujące przepływy.
VI mogą być wykorzystane do oszacowania Bayesa wiarygodnych przedziały dla parametrów modelu regresji do szacowania skutków różnych zabiegów lub zaobserwowanych cech dany rezultat zainteresowania. Przedziały wiarygodne wiążą wartości nieobserwowanego parametru z pewnym prawdopodobieństwem, zgodnie z rozkładem a posteriori parametru uwarunkowanym danymi obserwowanymi i przy założeniu wcześniejszego rozkładu parametru.
W tym Colab, pokażemy, jak korzystać z VI w celu uzyskania wiarygodnych przedziały dla parametrów liniowych bayesowskiej modelu regresji dla zmierzonych poziomów radonu w domach (z wykorzystaniem Gelman et al (2007) Radon zestawu danych. Patrz podobnych przykładów w stan). Pokażemy, jak TFP JointDistribution y połączyć z bijectors zbudować i dopasować dwa rodzaje ekspresyjnych posteriors zastępczych:
- standardowy rozkład normalny przekształcony przez macierz blokową. Macierz może odzwierciedlać niezależność niektórych elementów a posteriori i zależność między innymi, rozluźniając założenie a posteriori pola średniego lub pełnej kowariancji.
- bardziej skomplikowane, o większej pojemności odwrotny przepływ autoregresyjny .
Tylne części zastępcze są szkolone i porównywane z wynikami ze średniego pola zastępczego w odcinku tylnym linii bazowej, jak również z próbkami prawdy podstawowej z hamiltonianu Monte Carlo.
Przegląd Bayesowskiego wnioskowania wariacyjnego
Załóżmy, że mamy następujący proces generatywny, gdzie \(\theta\) reprezentuje losowe parametry \(\omega\) reprezentuje parametry deterministyczne, a \(x_i\) są cechy i \(y_i\) są wartości docelowe dla \(i=1,\ldots,n\) obserwowane punkty danych: \ begin {align } &\theta \sim r(\Theta) && \text{(Przed)}\ &\text{for } i = 1 \ldots n: \nonumber \ &\quad y_i \sim p(Y_i|x_i, \theta \ omega) && \ tekst {(Prawdopodobieństwo)} \ koniec {} wyrównanie
VI jest więc scharakteryzowany przez: $\newcommand{\E}{\operatorname{\mathbb{E} } } \newcommand{\K}{\operatorname{\mathbb{K} } } \newcommand{\defeq}{\overset {\tiny\text{def} }{=} } \DeclareMathOperator*{\argmin}{arg\,min}$
\ rozpocząć {align} - \ logP ({y_i} _I ^ N | {X_i} _I ^ n \ omega) & \ defeq - \ log \ Int \ textrm {d} \ theta \ R (\ theta) \ prod_i^np(y_i|x_i,\theta, \omega) && \text{(Naprawdę twarda całka)} \ &= -\log \int \textrm{d}\theta\, q(\theta) \frac{1 }{q(\theta)} r(\theta) \prod_i^np(y_i|x_i,\theta, \omega) && \text{(Mnożenie przez 1)}\ &\le - \int \textrm{d} \ theta \, Q (\ theta) \ log \ Frac {r (\ theta) \ prod_i ^ NP (y_i | x i \ theta \ omega)} {Q (\ theta)} && \ tekst {(nierówność Jensena )} \ & \ defeq \ e {Q (\ theta)} [- \ log P (y_i | x_i \ Theta \ omega)] + \ K [Q (\ theta), R (\ theta)] \ & \ defeq \text{expected negative log likelihood"} + \ text {kl regularizer"} \ end {align}
(Technicznie jesteśmy zakładając \(q\) jest absolutnie ciągła względem \(r\). Patrz także Nierówność Jensena ).
Ponieważ granica obowiązuje dla wszystkich q, jest oczywiście najściślejsza dla:
\[q^*,w^* = \argmin_{q \in \mathcal{Q},\omega\in\mathbb{R}^d} \left\{ \sum_i^n\E_{q(\Theta)}\left[ -\log p(y_i|x_i,\Theta, \omega) \right] + \K[q(\Theta), r(\Theta)] \right\}\]
Jeśli chodzi o terminologię, nazywamy
- \(q^*\) z "surogat posteriori", a
- \(\mathcal{Q}\) z "surogat rodziny."
\(\omega^*\) reprezentuje wartości maksymalnej wiarogodności deterministycznej parametrów na utratę VI. Zobacz tę ankietę , aby uzyskać więcej informacji na temat wariacyjnym wnioskowania.
Przykład: Bayesowska hierarchiczna regresja liniowa na pomiarach Radona
Radon to radioaktywny gaz, który dostaje się do domów przez punkty styku z ziemią. Jest to substancja rakotwórcza, która jest główną przyczyną raka płuc u osób niepalących. Poziom radonu różni się znacznie w zależności od gospodarstwa domowego.
Agencja Ochrony Środowiska przeprowadziła badanie poziomu radonu w 80 000 domów. Dwa ważne predyktory to:
- Piętro, na którym dokonano pomiaru (radon wyższy w piwnicach)
- Poziom uranu w hrabstwie (dodatnia korelacja z poziomem radonu)
Prognozowanie poziomu radonu w domach zgrupowane według powiatu jest klasycznym problemem Bayesa hierarchicznego modelowania, wprowadzony przez Gelman i Hill (2006) . Zbudujemy hierarchiczny model liniowy do przewidywania pomiarów radonu w domach, w którym hierarchia to grupowanie domów według powiatów. Interesują nas wiarygodne przedziały dla wpływu lokalizacji (hrabstwa) na poziom radonu domów w Minnesocie. Aby wyizolować ten efekt, w modelu uwzględniono również wpływ poziomu podłogi i uranu. Dodatkowo uwzględnimy efekt kontekstowy odpowiadający średniemu piętrze, na którym dokonano pomiaru, według powiatu, tak że jeśli istnieje różnica między powiatami piętra, na którym wykonano pomiary, nie jest to przypisywane efektowi powiatu.
pip3 install -q tf-nightly tfp-nightly
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
import warnings
tfd = tfp.distributions
tfb = tfp.bijectors
plt.rcParams['figure.facecolor'] = '1.'
# Load the Radon dataset from `tensorflow_datasets` and filter to data from
# Minnesota.
dataset = tfds.as_numpy(
tfds.load('radon', split='train').filter(
lambda x: x['features']['state'] == 'MN').batch(10**9))
# Dependent variable: Radon measurements by house.
dataset = next(iter(dataset))
radon_measurement = dataset['activity'].astype(np.float32)
radon_measurement[radon_measurement <= 0.] = 0.1
log_radon = np.log(radon_measurement)
# Measured uranium concentrations in surrounding soil.
uranium_measurement = dataset['features']['Uppm'].astype(np.float32)
log_uranium = np.log(uranium_measurement)
# County indicator.
county_strings = dataset['features']['county'].astype('U13')
unique_counties, county = np.unique(county_strings, return_inverse=True)
county = county.astype(np.int32)
num_counties = unique_counties.size
# Floor on which the measurement was taken.
floor_of_house = dataset['features']['floor'].astype(np.int32)
# Average floor by county (contextual effect).
county_mean_floor = []
for i in range(num_counties):
county_mean_floor.append(floor_of_house[county == i].mean())
county_mean_floor = np.array(county_mean_floor, dtype=log_radon.dtype)
floor_by_county = county_mean_floor[county]
Model regresji jest określony w następujący sposób:
\(\newcommand{\Normal}{\operatorname{\sf Normal} }\)\ rozpocząć {align} & \ tekst {uranium_weight} \ SIM \ normalna (0, 1) \ & \ tekst {county_floor_weight} \ SIM \ normalna (0, 1) \ & \ tekst {do} j = 1 \ ldots \text{liczba_hrabstw}:\ &\quad \text{county_effect}_j \sim \Normal (0, \sigma_c)\ &\text{for } i = 1\ldots n:\ &\quad \mu_i = ( \ & \ quad \ quad \ tekst {Odchylenie} \ & \ quad \ quad + \ tekst {efekt hrabstwo} {\ tekst {hrabstwo} _I} \ & \ quad \ quad + \ tekst {log_uranium} _I \ tekst Times \ {uranium_weight } \ & \ quad \ quad + \ tekst {floor_of_house} _I \ times \ tekst {floor_weight} \ & \ quad \ quad + \ tekst {hrabstwo floor_by} {\ tekst {hrabstwo} _I} \ tekst Times \ {county_floor_weight}) \ & \ quad \ tekst {log_radon} _I \ SIM \ normalna (\ mu_i \ sigma_y) \ koniec {wyrównanie} w którym \(i\) indeksy uwagi i \(\text{county}_i\) jest powiat w którym \(i\)p obserwacji wynosił zajęty.
Używamy efektu losowego na poziomie hrabstwa, aby uchwycić zróżnicowanie geograficzne. Parametry uranium_weight i county_floor_weight modeluje probabilistycznie i floor_weight a stałe bias są deterministyczny. Te wybory modelowania są w dużej mierze arbitralne i są dokonywane w celu zademonstrowania VI na modelu probabilistycznym o rozsądnej złożoności. Dla bardziej wnikliwej dyskusji wielopoziomowego modelowania ze stałymi i efektów losowych w TFP, przy użyciu zestawu danych radonu, zobacz wielopoziomowego Modeling Primer i dopasowywania uogólnionych Linear Mixed efekty modele Korzystanie wariacyjnymi Wnioskowanie .
# Create variables for fixed effects.
floor_weight = tf.Variable(0.)
bias = tf.Variable(0.)
# Variables for scale parameters.
log_radon_scale = tfp.util.TransformedVariable(1., tfb.Exp())
county_effect_scale = tfp.util.TransformedVariable(1., tfb.Exp())
# Define the probabilistic graphical model as a JointDistribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
uranium_weight = yield tfd.Normal(0., scale=1., name='uranium_weight')
county_floor_weight = yield tfd.Normal(
0., scale=1., name='county_floor_weight')
county_effect = yield tfd.Sample(
tfd.Normal(0., scale=county_effect_scale),
sample_shape=[num_counties], name='county_effect')
yield tfd.Normal(
loc=(log_uranium * uranium_weight + floor_of_house* floor_weight
+ floor_by_county * county_floor_weight
+ tf.gather(county_effect, county, axis=-1)
+ bias),
scale=log_radon_scale[..., tf.newaxis],
name='log_radon')
# Pin the observed `log_radon` values to model the un-normalized posterior.
target_model = model.experimental_pin(log_radon=log_radon)
Wyraziste zastępcze potyły
Następnie szacujemy rozkłady a posteriori efektów losowych za pomocą VI z dwoma różnymi typami zastępczych a posterioriów:
- Ograniczony wielowymiarowy rozkład normalny ze strukturą kowariancji indukowaną przez blokową transformację macierzy.
- Standardowy rozkład wielu zmiennych Normal zwerbowany przez Inverse autoregresyjnych przepływu , który jest następnie podzielony i restrukturyzacji, aby dopasować wsparcie tylnej.
Wielowymiarowy Prawidłowy zastępczy tylny
Aby zbudować ten zastępczy tył, używany jest wyszkolony operator liniowy, który indukuje korelację między komponentami odcinka tylnego.
# Determine the `event_shape` of the posterior, and calculate the size of each
# `event_shape` component. These determine the sizes of the components of the
# underlying standard Normal distribution, and the dimensions of the blocks in
# the blockwise matrix transformation.
event_shape = target_model.event_shape_tensor()
flat_event_shape = tf.nest.flatten(event_shape)
flat_event_size = tf.nest.map_structure(tf.reduce_prod, flat_event_shape)
# The `event_space_bijector` maps unconstrained values (in R^n) to the support
# of the prior -- we'll need this at the end to constrain Multivariate Normal
# samples to the prior's support.
event_space_bijector = target_model.experimental_default_event_space_bijector()
Skonstruować JointDistribution ze standardowych składników wektor normalny, z wartościami ustalonych wymiarach od odpowiednich poprzednich elementów. Składniki powinny mieć wartość wektorową, aby można je było przekształcić za pomocą operatora liniowego.
base_standard_dist = tfd.JointDistributionSequential(
[tfd.Sample(tfd.Normal(0., 1.), s) for s in flat_event_size])
Zbuduj nadającego się do trenowania operatora liniowego w kształcie dolnego trójkąta. Zastosujemy go do standardowego rozkładu normalnego, aby zaimplementować (uczącą się) transformację macierzy blokowej i wywołać strukturę korelacji a posteriori.
W operatora blokowo liniowego nadający się do szkolenia pełny blok reprezentuje macierz kowariancji pełnej pomiędzy dwoma składnikami tylnej, podczas gdy blok zerowe (lub None ) wyraża niezależność. Bloki na przekątnej są macierzami trójkątnymi dolnymi lub macierzami diagonalnymi, tak że cała struktura blokowa reprezentuje macierz trójkątną dolną.
Zastosowanie tego bijectora do rozkładu bazowego daje wielowymiarowy rozkład normalny ze średnią 0 i (współczynnikiem Cholesky'ego) kowariancją równą macierzy bloków trójkąta dolnego.
operators = (
(tf.linalg.LinearOperatorDiag,), # Variance of uranium weight (scalar).
(tf.linalg.LinearOperatorFullMatrix, # Covariance between uranium and floor-by-county weights.
tf.linalg.LinearOperatorDiag), # Variance of floor-by-county weight (scalar).
(None, # Independence between uranium weight and county effects.
None, # Independence between floor-by-county and county effects.
tf.linalg.LinearOperatorDiag) # Independence among the 85 county effects.
)
block_tril_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
scale_bijector = tfb.ScaleMatvecLinearOperatorBlock(block_tril_linop)
Po zastosowaniu operatora liniowego do standardowego rozkładu normalnego, zastosować wieloczęściowy Shift bijector aby umożliwić podjęcie średnią wartości niezerowe.
loc_bijector = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
Wynikowy wielowymiarowy rozkład normalny, uzyskany przez przekształcenie standardowego rozkładu normalnego za pomocą bijektorów skali i lokalizacji, musi zostać przekształcony i zrestrukturyzowany w celu dopasowania do poprzedniego, a ostatecznie ograniczony do wsparcia poprzedniego.
# Reshape each component to match the prior, using a nested structure of
# `Reshape` bijectors wrapped in `JointMap` to form a multipart bijector.
reshape_bijector = tfb.JointMap(
tf.nest.map_structure(tfb.Reshape, flat_event_shape))
# Restructure the flat list of components to match the prior's structure
unflatten_bijector = tfb.Restructure(
tf.nest.pack_sequence_as(
event_shape, range(len(flat_event_shape))))
Teraz zbierz to wszystko razem — połącz ze sobą nadających się do wytrenowania bijektorów i zastosuj je do podstawowego standardowego rozkładu normalnego, aby skonstruować zastępczy a posteriori.
surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
loc_bijector, # allow for nonzero mean
scale_bijector # apply the block matrix transformation to the standard Normal distribution
]))
Trenuj wielowymiarową normalną tylną surogację.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
mvn_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mvn_samples = surrogate_posterior.sample(1000)
mvn_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mvn_samples)
- surrogate_posterior.log_prob(mvn_samples))
print('Multivariate Normal surrogate posterior ELBO: {}'.format(mvn_final_elbo))
plt.plot(mvn_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Multivariate Normal surrogate posterior ELBO: -1065.705322265625
Ponieważ wytrenowany substytut a posteriori jest rozkładem TFP, możemy pobrać z niego próbki i przetworzyć je w celu uzyskania wiarygodnych przedziałów a posteriori dla parametrów.
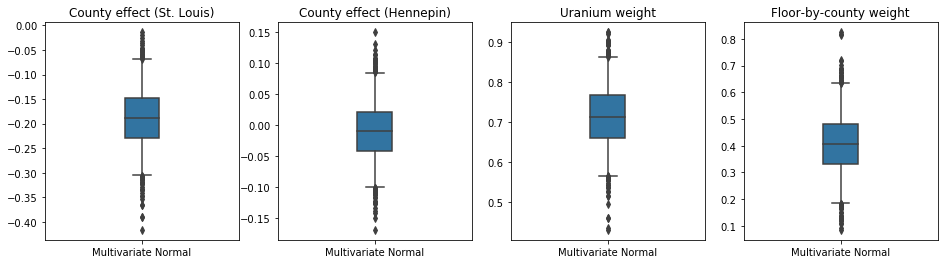
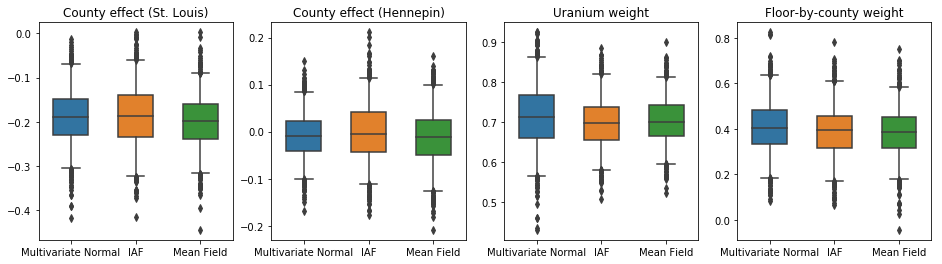
Poniższe wykresy pudełkowe-i-wąsy pokazują 50% i 95% wiarygodne przedziały dla efektu powiatu dwóch największych powiatów i wagi regresji na pomiarach uranu w glebie i średnim piętrze powiatu. Wiarygodność a posteriori przedziałów dla efektów hrabstwa wskazuje, że lokalizacja w hrabstwie St. Louis jest związana z niższymi poziomami radonu, po uwzględnieniu innych zmiennych, oraz że wpływ lokalizacji w hrabstwie Hennepin jest prawie neutralny.
Wiarygodne przedziały wag regresji z tyłu pokazują, że wyższe poziomy uranu w glebie są powiązane z wyższymi poziomami radonu, a hrabstwa, w których pomiary były wykonywane na wyższych piętrach (prawdopodobnie dlatego, że dom nie był podpiwniczony) zwykle mają wyższy poziom radonu. które mogą odnosić się do właściwości gruntu i ich wpływu na rodzaj budowanych konstrukcji.
(deterministyczny) współczynnik stropów jest ujemny, co wskazuje, że w niższych kondygnacjach poziom radonu jest wyższy, zgodnie z oczekiwaniami.
st_louis_co = 69 # Index of St. Louis, the county with the most observations.
hennepin_co = 25 # Index of Hennepin, with the second-most observations.
def pack_samples(samples):
return {'County effect (St. Louis)': samples.county_effect[..., st_louis_co],
'County effect (Hennepin)': samples.county_effect[..., hennepin_co],
'Uranium weight': samples.uranium_weight,
'Floor-by-county weight': samples.county_floor_weight}
def plot_boxplot(posterior_samples):
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
# Invert the results dict for easier plotting.
k = list(posterior_samples.values())[0].keys()
plot_results = {
v: {p: posterior_samples[p][v] for p in posterior_samples} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
sns.boxplot(data=list(var_results.values()), ax=axes[i],
width=0.18*len(var_results), whis=(2.5, 97.5))
# axes[i].boxplot(list(var_results.values()), whis=(2.5, 97.5))
axes[i].title.set_text(var)
fs = 10 if len(var_results) < 4 else 8
axes[i].set_xticklabels(list(var_results.keys()), fontsize=fs)
results = {'Multivariate Normal': pack_samples(mvn_samples)}
print('Bias is: {:.2f}'.format(bias.numpy()))
print('Floor fixed effect is: {:.2f}'.format(floor_weight.numpy()))
plot_boxplot(results)
Bias is: 1.40 Floor fixed effect is: -0.72
Odwrotny autoregresyjny przepływ zastępczy tylny
Odwrotne przepływy autoregresyjne (IAF) to normalizujące przepływy, które wykorzystują sieci neuronowe do przechwytywania złożonych, nieliniowych zależności między składnikami rozkładu. Następnie tworzymy zastępczy model IAF a posteriori, aby sprawdzić, czy ten bardziej elastyczny model o większej wydajności przewyższa ograniczoną wielowymiarową normalną.
# Build a standard Normal with a vector `event_shape`, with length equal to the
# total number of degrees of freedom in the posterior.
base_distribution = tfd.Sample(
tfd.Normal(0., 1.), sample_shape=[tf.reduce_sum(flat_event_size)])
# Apply an IAF to the base distribution.
num_iafs = 2
iaf_bijectors = [
tfb.Invert(tfb.MaskedAutoregressiveFlow(
shift_and_log_scale_fn=tfb.AutoregressiveNetwork(
params=2, hidden_units=[256, 256], activation='relu')))
for _ in range(num_iafs)
]
# Split the base distribution's `event_shape` into components that are equal
# in size to the prior's components.
split = tfb.Split(flat_event_size)
# Chain these bijectors and apply them to the standard Normal base distribution
# to build the surrogate posterior. `event_space_bijector`,
# `unflatten_bijector`, and `reshape_bijector` are the same as in the
# multivariate Normal surrogate posterior.
iaf_surrogate_posterior = tfd.TransformedDistribution(
base_distribution,
bijector=tfb.Chain([
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the prior
reshape_bijector, # reshape the vector-valued components to match the shapes of the prior components
split] + # Split the samples into components of the same size as the prior components
iaf_bijectors # Apply a flow model to the Tensor-valued standard Normal distribution
))
Trenuj tylną zastępcę IAF.
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
iaf_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
iaf_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=4,
jit_compile=True)
iaf_samples = iaf_surrogate_posterior.sample(1000)
iaf_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*iaf_samples)
- iaf_surrogate_posterior.log_prob(iaf_samples))
print('IAF surrogate posterior ELBO: {}'.format(iaf_final_elbo))
plt.plot(iaf_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
IAF surrogate posterior ELBO: -1065.3663330078125
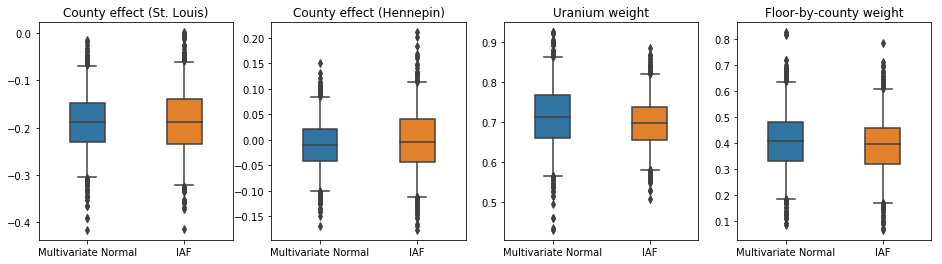
Wiarygodne odstępy dla zastępczej części tylnej IAF wydają się podobne do tych dla ograniczonej wielowymiarowej normy.
results['IAF'] = pack_samples(iaf_samples)
plot_boxplot(results)
Linia bazowa: substytut średniego pola tylnego
Często zakłada się, że zastępcze a posteriori VI to rozkłady normalne pola średniego (niezależne), z możliwymi do trenowania średnimi i wariancjami, które są ograniczone do wsparcia a priori z transformacją bijektywną. Definiujemy zastępczy tył o średnim polu oprócz dwóch bardziej wyrazistych zastępczych tylnych części ciała, stosując ten sam ogólny wzór, co wieloczynnikowy normalny zastępczy tylny tył.
# A block-diagonal linear operator, in which each block is a diagonal operator,
# transforms the standard Normal base distribution to produce a mean-field
# surrogate posterior.
operators = (tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag)
block_diag_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
mean_field_scale = tfb.ScaleMatvecLinearOperatorBlock(block_diag_linop)
mean_field_loc = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
mean_field_surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
mean_field_loc, # allow for nonzero mean
mean_field_scale # apply the block matrix transformation to the standard Normal distribution
]))
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
mean_field_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
mean_field_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mean_field_samples = mean_field_surrogate_posterior.sample(1000)
mean_field_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mean_field_samples)
- mean_field_surrogate_posterior.log_prob(mean_field_samples))
print('Mean-field surrogate posterior ELBO: {}'.format(mean_field_final_elbo))
plt.plot(mean_field_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Mean-field surrogate posterior ELBO: -1065.7652587890625
W tym przypadku średnie pole zastępcze tylne daje podobne wyniki do bardziej wyrazistych zastępczych tylnych, co wskazuje, że ten prostszy model może być odpowiedni do zadania wnioskowania.
results['Mean Field'] = pack_samples(mean_field_samples)
plot_boxplot(results)
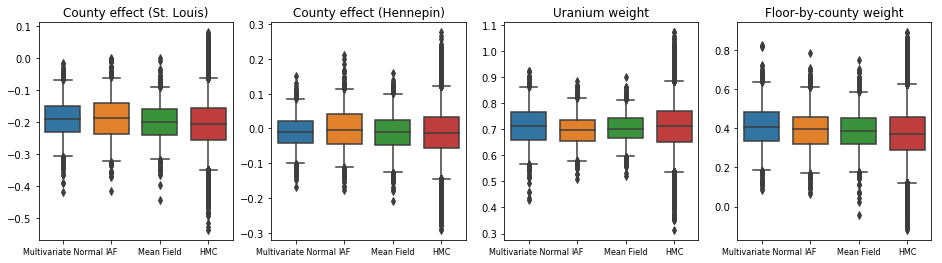
Prawda podstawowa: hamiltonian Monte Carlo (HMC)
Używamy HMC do generowania próbek „prawdziwych podstaw” z prawdziwego odcinka tylnego, w celu porównania z wynikami zastępczych zębów tylnych.
num_chains = 8
num_leapfrog_steps = 3
step_size = 0.4
num_steps=20000
flat_event_shape = tf.nest.flatten(target_model.event_shape)
enum_components = list(range(len(flat_event_shape)))
bijector = tfb.Restructure(
enum_components,
tf.nest.pack_sequence_as(target_model.event_shape, enum_components))(
target_model.experimental_default_event_space_bijector())
current_state = bijector(
tf.nest.map_structure(
lambda e: tf.zeros([num_chains] + list(e), dtype=tf.float32),
target_model.event_shape))
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_model.unnormalized_log_prob,
num_leapfrog_steps=num_leapfrog_steps,
step_size=[tf.fill(s.shape, step_size) for s in current_state])
hmc = tfp.mcmc.TransformedTransitionKernel(
hmc, bijector)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(num_steps // 2 * 0.8),
target_accept_prob=0.9)
chain, is_accepted = tf.function(
lambda current_state: tfp.mcmc.sample_chain(
current_state=current_state,
kernel=hmc,
num_results=num_steps // 2,
num_burnin_steps=num_steps // 2,
trace_fn=lambda _, pkr:
(pkr.inner_results.inner_results.is_accepted),
),
autograph=False,
jit_compile=True)(current_state)
accept_rate = tf.reduce_mean(tf.cast(is_accepted, tf.float32))
ess = tf.nest.map_structure(
lambda c: tfp.mcmc.effective_sample_size(
c,
cross_chain_dims=1,
filter_beyond_positive_pairs=True),
chain)
r_hat = tf.nest.map_structure(tfp.mcmc.potential_scale_reduction, chain)
hmc_samples = pack_samples(
tf.nest.pack_sequence_as(target_model.event_shape, chain))
print('Acceptance rate is {}'.format(accept_rate))
Acceptance rate is 0.9008625149726868
Wykreśl ślady próbek w celu sprawdzenia wyników HMC.
def plot_traces(var_name, samples):
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
s = samples.numpy()[:, chain]
axes[0].plot(s, alpha=0.7)
sns.kdeplot(s, ax=axes[1], shade=False)
axes[0].title.set_text("'{}' trace".format(var_name))
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
warnings.filterwarnings('ignore')
for var, var_samples in hmc_samples.items():
plot_traces(var, var_samples)




Wszystkie trzy zastępcze a posteriori tworzyły wiarygodne odstępy, które są wizualnie podobne do próbek HMC, choć czasami są słabo rozproszone ze względu na efekt utraty ELBO, co jest powszechne w VI.
results['HMC'] = hmc_samples
plot_boxplot(results)
Dodatkowe wyniki
Funkcje kreślenia
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'medium'})
def plot_loss_and_elbo():
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].scatter([0, 1, 2],
[mvn_final_elbo.numpy(),
iaf_final_elbo.numpy(),
mean_field_final_elbo.numpy()])
axes[0].set_xticks(ticks=[0, 1, 2])
axes[0].set_xticklabels(labels=[
'Multivariate Normal', 'IAF', 'Mean Field'])
axes[0].title.set_text('Evidence Lower Bound (ELBO)')
axes[1].plot(mvn_loss, label='Multivariate Normal')
axes[1].plot(iaf_loss, label='IAF')
axes[1].plot(mean_field_loss, label='Mean Field')
axes[1].set_ylim([1000, 4000])
axes[1].set_xlabel('Training step')
axes[1].set_ylabel('Loss (negative ELBO)')
axes[1].title.set_text('Loss')
plt.legend()
plt.show()
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'small'})
def plot_kdes(num_chains=8):
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
k = list(results.values())[0].keys()
plot_results = {
v: {p: results[p][v] for p in results} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
ax = axes[i % 2, i // 2]
for posterior, posterior_results in var_results.items():
if posterior == 'HMC':
label = posterior
for chain in range(num_chains):
sns.kdeplot(
posterior_results[:, chain],
ax=ax, shade=False, color='k', linestyle=':', label=label)
label=None
else:
sns.kdeplot(
posterior_results, ax=ax, shade=False, label=posterior)
ax.title.set_text('{}'.format(var))
ax.legend()
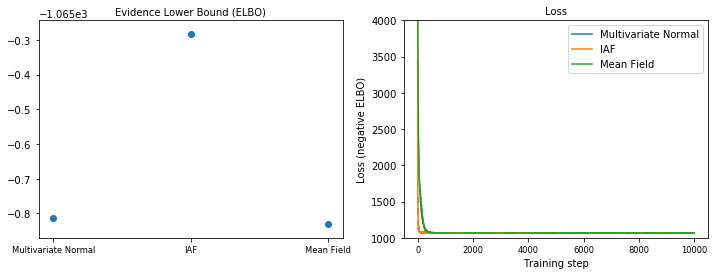
Dolna granica dowodów (ELBO)
IAF, zdecydowanie największa i najbardziej elastyczna tylna część zastępcza, zbiega się do najwyższej dolnej granicy dowodów (ELBO).
plot_loss_and_elbo()
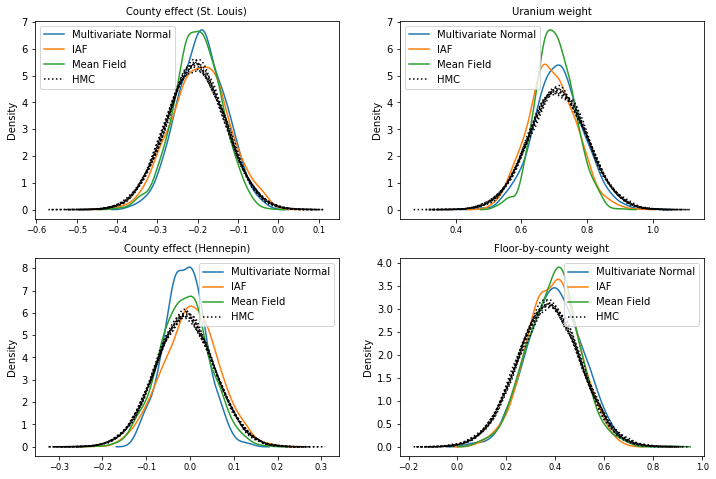
Próbki tylne
Próbki z każdego zastępczego tylnego odcinka w porównaniu z próbkami gruntu HMC (inna wizualizacja próbek pokazanych na wykresach pudełkowych).
plot_kdes()
Wniosek
W tym Colab zbudowaliśmy zastępcze posteriors VI za pomocą rozkładów stawów i wieloczęściowych bijektorów i dopasowaliśmy je do oszacowania wiarygodnych przedziałów dla wag w modelu regresji na zbiorze danych radonu. W przypadku tego prostego modelu, bardziej wyraziste zastępcze zęby tylne były wykonywane podobnie do zastępczych tylnych części ciała o średnim polu. Zademonstrowane przez nas narzędzia można jednak wykorzystać do budowy szerokiej gamy elastycznych zastępczych zębów bocznych odpowiednich dla bardziej złożonych modeli.
