Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza l'origine su GitHub Visualizza l'origine su GitHub |  Scarica quaderno Scarica quaderno |
Il rumore è presente nei moderni computer quantistici. I qubit sono suscettibili alle interferenze dell'ambiente circostante, alla fabbricazione imperfetta, ai TLS e talvolta anche ai raggi gamma . Fino a quando non si raggiunge la correzione degli errori su larga scala, gli algoritmi odierni devono essere in grado di rimanere funzionali in presenza di rumore. Ciò rende il test degli algoritmi sotto rumore un passaggio importante per la convalida degli algoritmi/modelli quantistici che funzioneranno sui computer quantistici di oggi.
In questo tutorial esplorerai le basi della simulazione di circuiti rumorosi in TFQ tramite l'API tfq.layers di alto livello.
Impostare
pip install tensorflow==2.7.0 tensorflow-quantum
pip install -q git+https://github.com/tensorflow/docs
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
import random
import cirq
import sympy
import tensorflow_quantum as tfq
import tensorflow as tf
import numpy as np
# Plotting
import matplotlib.pyplot as plt
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
2022-02-04 12:35:30.853880: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Comprendere il rumore quantistico
1.1 Rumore del circuito di base
Il rumore su un computer quantistico influisce sui campioni di stringhe di bit che puoi misurare da esso. Un modo intuitivo in cui puoi iniziare a pensarci è che un computer quantistico rumoroso "inserirà", "eliminerà" o "sostituirà" le porte in luoghi casuali come il diagramma seguente:
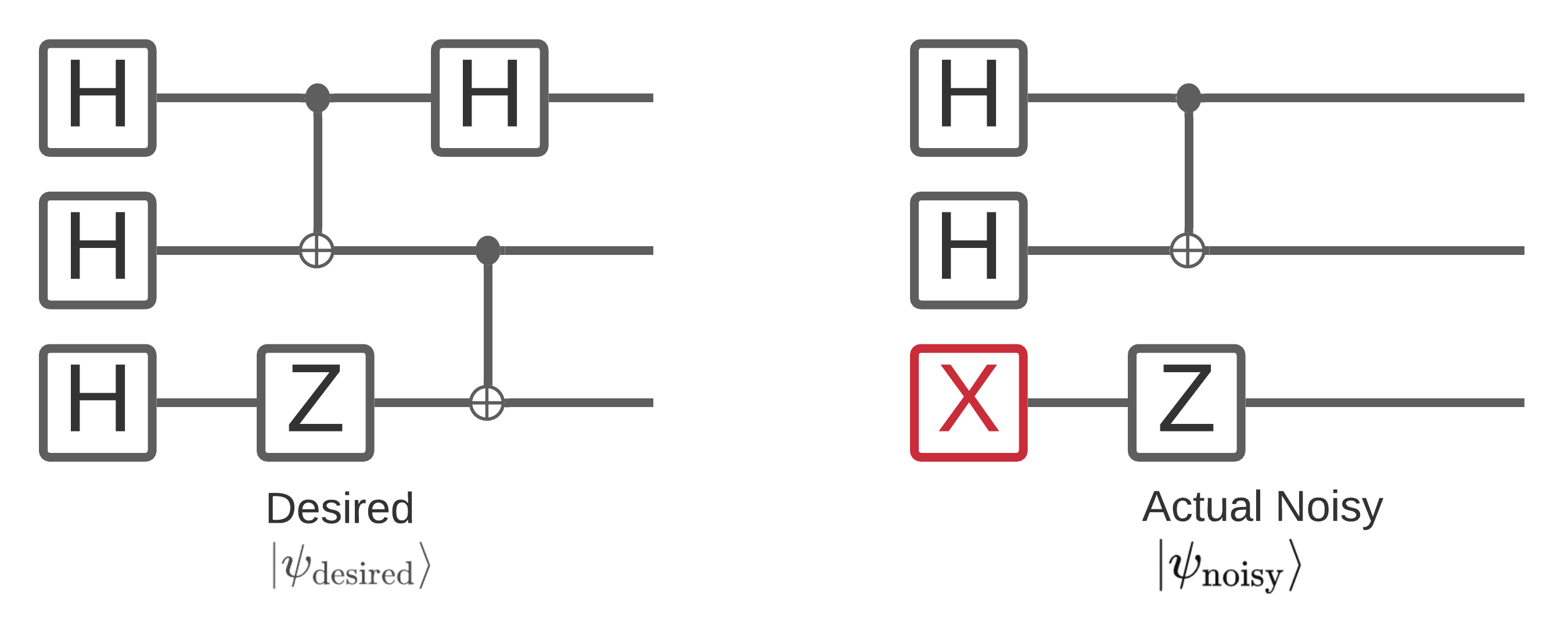
Basandosi su questa intuizione, quando si ha a che fare con il rumore, non si utilizza più un singolo stato puro \(|\psi \rangle\) ma si ha invece a che fare con un insieme di tutte le possibili realizzazioni rumorose del circuito desiderato: \(\rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |\) . Dove \(p_j\) fornisce la probabilità che il sistema sia in \(|\psi_j \rangle\) .
Rivisitando l'immagine sopra, se sapessimo in anticipo che il 90% delle volte il nostro sistema ha funzionato perfettamente, o ha sbagliato il 10% delle volte con solo questa modalità di errore, allora il nostro insieme sarebbe:
\(\rho = 0.9 |\psi_\text{desired} \rangle \langle \psi_\text{desired}| + 0.1 |\psi_\text{noisy} \rangle \langle \psi_\text{noisy}| \)
Se ci fosse più di un solo modo in cui il nostro circuito potrebbe sbagliare, l'insieme \(\rho\) conterrebbe più di due termini (uno per ogni nuova realizzazione rumorosa che potrebbe verificarsi). \(\rho\) è indicato come la matrice di densità che descrive il sistema rumoroso.
1.2 Utilizzo dei canali per modellare il rumore del circuito
Sfortunatamente in pratica è quasi impossibile conoscere tutti i modi in cui il tuo circuito potrebbe sbagliare e le loro esatte probabilità. Un presupposto semplificativo che puoi fare è che dopo ogni operazione nel tuo circuito c'è una sorta di canale che cattura approssimativamente come quell'operazione potrebbe essere un errore. Puoi creare rapidamente un circuito con un po' di rumore:
def x_circuit(qubits):
"""Produces an X wall circuit on `qubits`."""
return cirq.Circuit(cirq.X.on_each(*qubits))
def make_noisy(circuit, p):
"""Add a depolarization channel to all qubits in `circuit` before measurement."""
return circuit + cirq.Circuit(cirq.depolarize(p).on_each(*circuit.all_qubits()))
my_qubits = cirq.GridQubit.rect(1, 2)
my_circuit = x_circuit(my_qubits)
my_noisy_circuit = make_noisy(my_circuit, 0.5)
my_circuit
my_noisy_circuit
È possibile esaminare la matrice di densità silenziosa \(\rho\) con:
rho = cirq.final_density_matrix(my_circuit)
np.round(rho, 3)
array([[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j]], dtype=complex64)
E la matrice di densità rumorosa \(\rho\) con:
rho = cirq.final_density_matrix(my_noisy_circuit)
np.round(rho, 3)
array([[0.111+0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.222+0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0.222+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0.444+0.j]], dtype=complex64)
Confrontando i due diversi \( \rho \) si può notare che il rumore ha influenzato le ampiezze dello stato (e di conseguenza le probabilità di campionamento). Nel caso silenzioso ti aspetteresti sempre di campionare lo stato \( |11\rangle \) . Ma nello stato rumoroso ora c'è una probabilità diversa da zero di campionare anche \( |00\rangle \) o \( |01\rangle \) o \( |10\rangle \) :
"""Sample from my_noisy_circuit."""
def plot_samples(circuit):
samples = cirq.sample(circuit + cirq.measure(*circuit.all_qubits(), key='bits'), repetitions=1000)
freqs, _ = np.histogram(samples.data['bits'], bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
plot_samples(my_noisy_circuit)
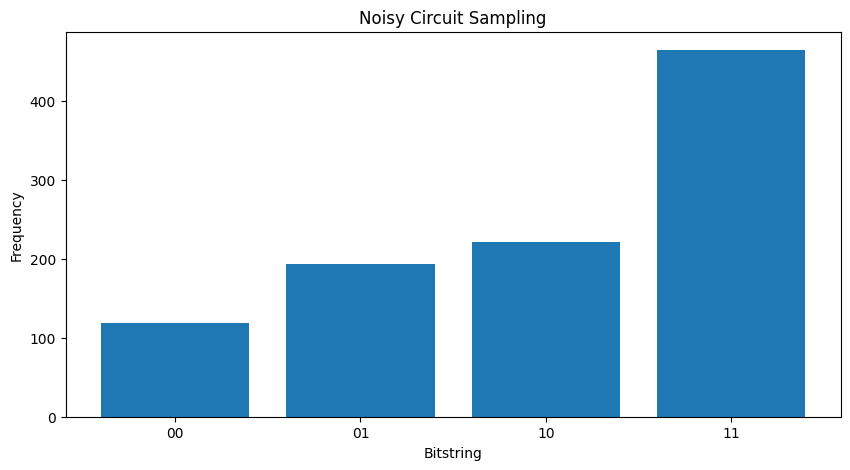
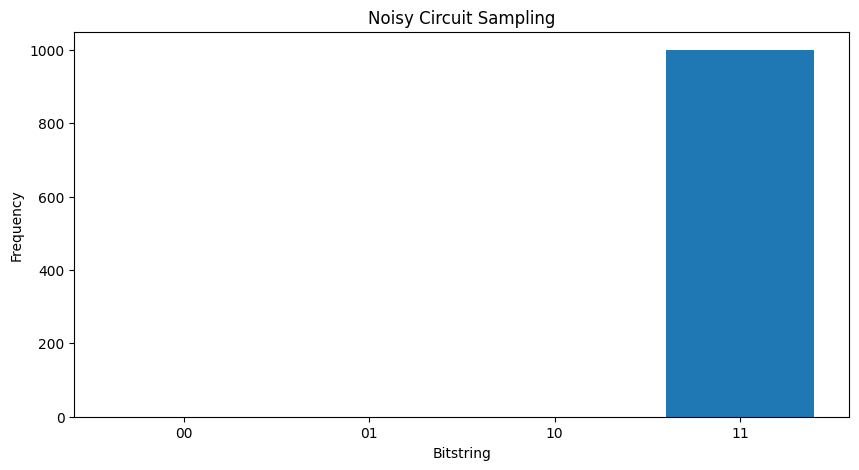
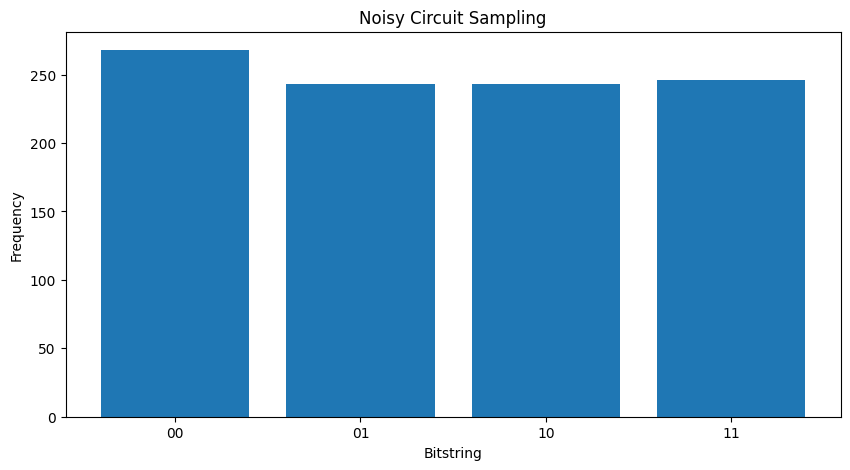
Senza alcun rumore otterrai sempre \(|11\rangle\):
"""Sample from my_circuit."""
plot_samples(my_circuit)
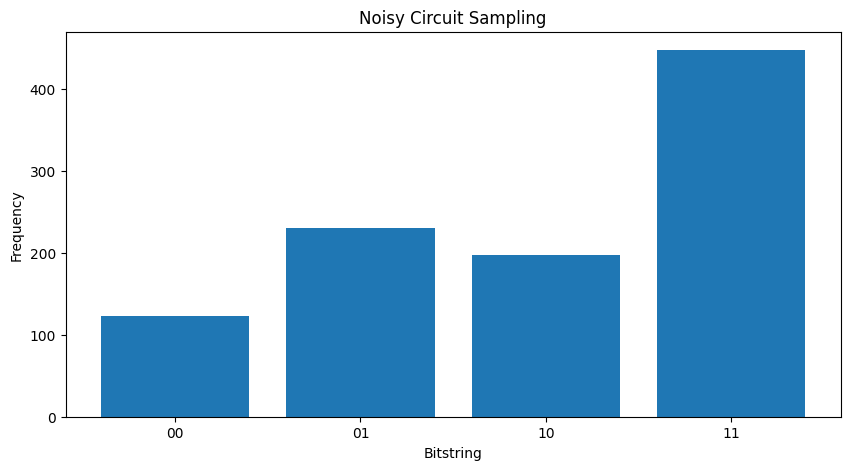
Se aumenti ulteriormente il rumore, diventerà sempre più difficile distinguere il comportamento desiderato (campionamento \(|11\rangle\) ) dal rumore:
my_really_noisy_circuit = make_noisy(my_circuit, 0.75)
plot_samples(my_really_noisy_circuit)
2. Rumore di base in TFQ
Con questa comprensione di come il rumore può influire sull'esecuzione del circuito, puoi esplorare come funziona il rumore in TFQ. TensorFlow Quantum utilizza la simulazione monte-carlo/basata sulla traiettoria come alternativa alla simulazione della matrice di densità. Questo perché la complessità della memoria della simulazione della matrice di densità limita le simulazioni di grandi dimensioni a <= 20 qubit con i tradizionali metodi di simulazione della matrice a densità piena. Monte-carlo / traiettoria scambia questo costo in memoria con un costo aggiuntivo nel tempo. L'opzione backend='noisy' è disponibile per tutti tfq.layers.Sample , tfq.layers.SampledExpectation e tfq.layers.Expectation (nel caso di Expectation questo aggiunge un parametro di repetitions richiesto).
2.1 Campionamento rumoroso in TFQ
Per ricreare i grafici di cui sopra usando TFQ e la simulazione della traiettoria puoi usare tfq.layers.Sample
"""Draw bitstring samples from `my_noisy_circuit`"""
bitstrings = tfq.layers.Sample(backend='noisy')(my_noisy_circuit, repetitions=1000)
numeric_values = np.einsum('ijk,k->ij', bitstrings.to_tensor().numpy(), [1, 2])[0]
freqs, _ = np.histogram(numeric_values, bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
<BarContainer object of 4 artists>
2.2 Aspettativa basata su campioni rumorosi
Per eseguire calcoli di aspettativa basati su campioni rumorosi è possibile utilizzare tfq.layers.SampleExpectation :
some_observables = [cirq.X(my_qubits[0]), cirq.Z(my_qubits[0]), 3.0 * cirq.Y(my_qubits[1]) + 1]
some_observables
[cirq.X(cirq.GridQubit(0, 0)),
cirq.Z(cirq.GridQubit(0, 0)),
cirq.PauliSum(cirq.LinearDict({frozenset({(cirq.GridQubit(0, 1), cirq.Y)}): (3+0j), frozenset(): (1+0j)}))]
Calcola le stime di aspettativa senza rumore tramite campionamento dal circuito:
noiseless_sampled_expectation = tfq.layers.SampledExpectation(backend='noiseless')(
my_circuit, operators=some_observables, repetitions=10000
)
noiseless_sampled_expectation.numpy()
array([[-0.0028, -1. , 1.0264]], dtype=float32)
Confronta quelli con le versioni rumorose:
noisy_sampled_expectation = tfq.layers.SampledExpectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_sampled_expectation.numpy()
array([[ 0.0242 , -0.33200002, 1.0138001 ],
[ 0.0108 , -0.0012 , 0.9502 ]], dtype=float32)
Puoi vedere che il rumore ha avuto un impatto particolare sulla precisione \(\langle \psi | Z | \psi \rangle\) , con my_really_noisy_circuit si è concentrato molto rapidamente verso 0.
2.3 Calcolo dell'aspettativa analitica rumorosa
L'esecuzione di rumorosi calcoli delle aspettative analitiche è quasi identica a quanto sopra:
noiseless_analytic_expectation = tfq.layers.Expectation(backend='noiseless')(
my_circuit, operators=some_observables
)
noiseless_analytic_expectation.numpy()
array([[ 1.9106853e-15, -1.0000000e+00, 1.0000002e+00]], dtype=float32)
noisy_analytic_expectation = tfq.layers.Expectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_analytic_expectation.numpy()
array([[ 1.9106850e-15, -3.3359998e-01, 1.0000000e+00],
[ 1.9106857e-15, -3.8000005e-03, 1.0000001e+00]], dtype=float32)
3. Modelli ibridi e rumore dei dati quantistici
Ora che hai implementato alcune simulazioni di circuiti rumorosi in TFQ, puoi sperimentare in che modo il rumore influisce sui modelli quantistici classici e ibridi, confrontando e confrontando le loro prestazioni rumorose e silenziose. Un buon primo controllo per vedere se un modello o un algoritmo è robusto al rumore consiste nel testare un modello depolarizzante a livello di circuito che assomiglia a questo:
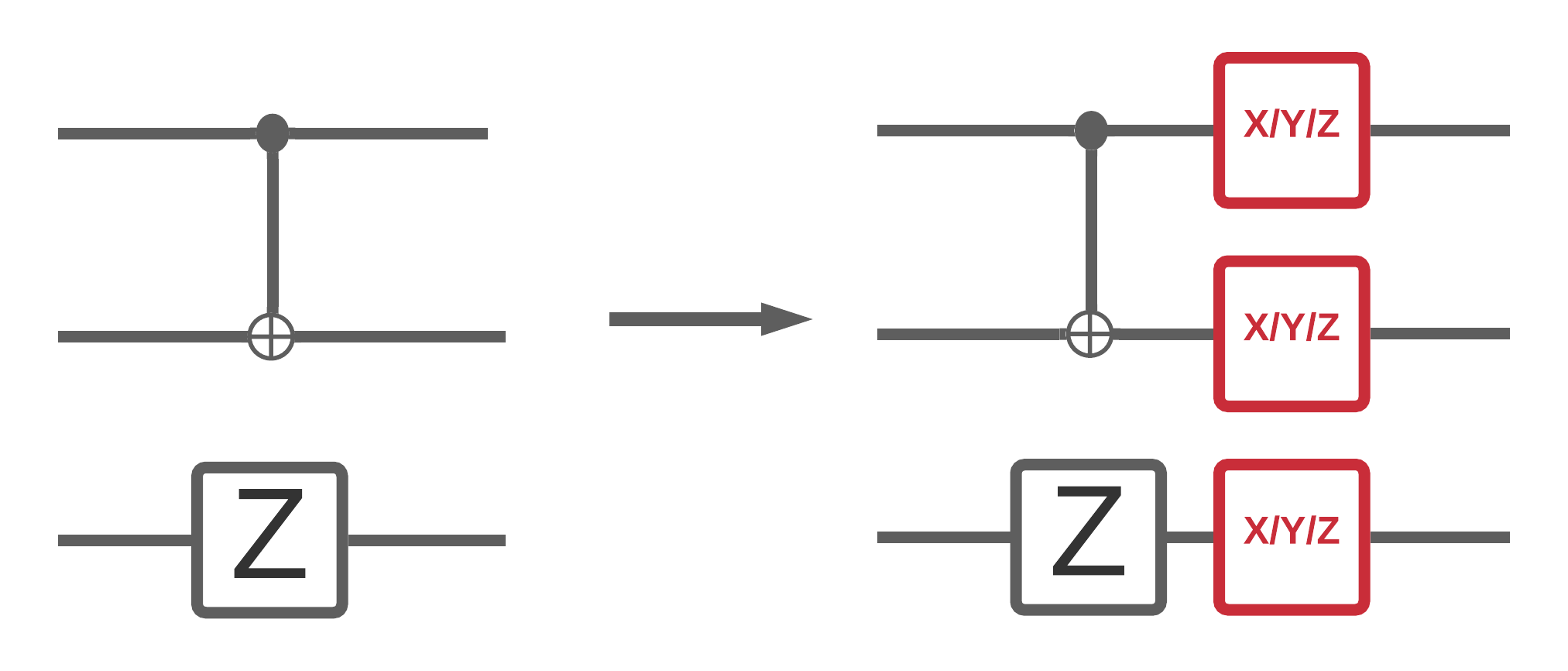
Dove ogni intervallo di tempo del circuito (a volte indicato come momento) ha un canale depolarizzante aggiunto dopo ogni operazione di gate in quell'intervallo di tempo. Il canale depolarizzante con applica uno di \(\{X, Y, Z \}\) con probabilità \(p\) o non applica nulla (mantieni l'operazione originale) con probabilità \(1-p\).
3.1 Dati
Per questo esempio puoi utilizzare alcuni circuiti preparati nel modulo tfq.datasets come dati di addestramento:
qubits = cirq.GridQubit.rect(1, 8)
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
circuits[0]
Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/quantum/spin_systems/XXZ_chain.zip 184451072/184449737 [==============================] - 2s 0us/step 184459264/184449737 [==============================] - 2s 0us/step
Scrivere una piccola funzione di supporto aiuterà a generare i dati per il caso rumoroso vs silenzioso:
def get_data(qubits, depolarize_p=0.):
"""Return quantum data circuits and labels in `tf.Tensor` form."""
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
if depolarize_p >= 1e-5:
circuits = [circuit.with_noise(cirq.depolarize(depolarize_p)) for circuit in circuits]
tmp = list(zip(circuits, labels))
random.shuffle(tmp)
circuits_tensor = tfq.convert_to_tensor([x[0] for x in tmp])
labels_tensor = tf.convert_to_tensor([x[1] for x in tmp])
return circuits_tensor, labels_tensor
3.2 Definire un circuito modello
Ora che hai dati quantistici sotto forma di circuiti, avrai bisogno di un circuito per modellare questi dati, come con i dati puoi scrivere una funzione di supporto per generare questo circuito che contiene facoltativamente rumore:
def modelling_circuit(qubits, depth, depolarize_p=0.):
"""A simple classifier circuit."""
dim = len(qubits)
ret = cirq.Circuit(cirq.H.on_each(*qubits))
for i in range(depth):
# Entangle layer.
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[::2], qubits[1::2]))
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[1::2], qubits[2::2]))
# Learnable rotation layer.
# i_params = sympy.symbols(f'layer-{i}-0:{dim}')
param = sympy.Symbol(f'layer-{i}')
single_qb = cirq.X
if i % 2 == 1:
single_qb = cirq.Y
ret += cirq.Circuit(single_qb(q) ** param for q in qubits)
if depolarize_p >= 1e-5:
ret = ret.with_noise(cirq.depolarize(depolarize_p))
return ret, [op(q) for q in qubits for op in [cirq.X, cirq.Y, cirq.Z]]
modelling_circuit(qubits, 3)[0]
3.3 Costruzione del modello e formazione
Con i dati e il circuito modello costruiti, la funzione di supporto finale di cui avrai bisogno è quella in grado di assemblare un tf.keras.Model ibrido quantistico rumoroso o silenzioso:
def build_keras_model(qubits, depolarize_p=0.):
"""Prepare a noisy hybrid quantum classical Keras model."""
spin_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
circuit_and_readout = modelling_circuit(qubits, 4, depolarize_p)
if depolarize_p >= 1e-5:
quantum_model = tfq.layers.NoisyPQC(*circuit_and_readout, sample_based=False, repetitions=10)(spin_input)
else:
quantum_model = tfq.layers.PQC(*circuit_and_readout)(spin_input)
intermediate = tf.keras.layers.Dense(4, activation='sigmoid')(quantum_model)
post_process = tf.keras.layers.Dense(1)(intermediate)
return tf.keras.Model(inputs=[spin_input], outputs=[post_process])
4. Confronta le prestazioni
4.1 Linea di base silenziosa
Con la generazione dei dati e il codice di costruzione del modello, ora puoi confrontare e confrontare le prestazioni del modello nelle impostazioni noiseless e noisey, prima puoi eseguire un training di riferimento senza rumore:
training_histories = dict()
depolarize_p = 0.
n_epochs = 50
phase_classifier = build_keras_model(qubits, depolarize_p)
phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
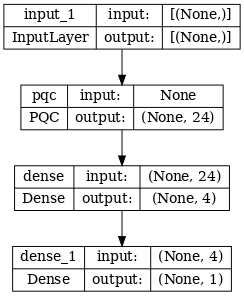
# Show the keras plot of the model
tf.keras.utils.plot_model(phase_classifier, show_shapes=True, dpi=70)
noiseless_data, noiseless_labels = get_data(qubits, depolarize_p)
training_histories['noiseless'] = phase_classifier.fit(x=noiseless_data,
y=noiseless_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 1s 133ms/step - loss: 0.7212 - accuracy: 0.4688 - val_loss: 0.6834 - val_accuracy: 0.5000 Epoch 2/50 4/4 [==============================] - 0s 80ms/step - loss: 0.6787 - accuracy: 0.4688 - val_loss: 0.6640 - val_accuracy: 0.5000 Epoch 3/50 4/4 [==============================] - 0s 76ms/step - loss: 0.6637 - accuracy: 0.4688 - val_loss: 0.6529 - val_accuracy: 0.5000 Epoch 4/50 4/4 [==============================] - 0s 78ms/step - loss: 0.6505 - accuracy: 0.4688 - val_loss: 0.6423 - val_accuracy: 0.5000 Epoch 5/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6409 - accuracy: 0.4688 - val_loss: 0.6322 - val_accuracy: 0.5000 Epoch 6/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6300 - accuracy: 0.4844 - val_loss: 0.6187 - val_accuracy: 0.5000 Epoch 7/50 4/4 [==============================] - 0s 77ms/step - loss: 0.6171 - accuracy: 0.5781 - val_loss: 0.6007 - val_accuracy: 0.5000 Epoch 8/50 4/4 [==============================] - 0s 79ms/step - loss: 0.6008 - accuracy: 0.6250 - val_loss: 0.5825 - val_accuracy: 0.5833 Epoch 9/50 4/4 [==============================] - 0s 76ms/step - loss: 0.5864 - accuracy: 0.6406 - val_loss: 0.5610 - val_accuracy: 0.6667 Epoch 10/50 4/4 [==============================] - 0s 77ms/step - loss: 0.5670 - accuracy: 0.6719 - val_loss: 0.5406 - val_accuracy: 0.8333 Epoch 11/50 4/4 [==============================] - 0s 79ms/step - loss: 0.5474 - accuracy: 0.6875 - val_loss: 0.5173 - val_accuracy: 0.9167 Epoch 12/50 4/4 [==============================] - 0s 77ms/step - loss: 0.5276 - accuracy: 0.7188 - val_loss: 0.4941 - val_accuracy: 0.9167 Epoch 13/50 4/4 [==============================] - 0s 75ms/step - loss: 0.5066 - accuracy: 0.7500 - val_loss: 0.4686 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4838 - accuracy: 0.7812 - val_loss: 0.4437 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4618 - accuracy: 0.8281 - val_loss: 0.4182 - val_accuracy: 0.9167 Epoch 16/50 4/4 [==============================] - 0s 76ms/step - loss: 0.4386 - accuracy: 0.8281 - val_loss: 0.3930 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 0s 79ms/step - loss: 0.4158 - accuracy: 0.8438 - val_loss: 0.3673 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 0s 79ms/step - loss: 0.3944 - accuracy: 0.8438 - val_loss: 0.3429 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 0s 77ms/step - loss: 0.3735 - accuracy: 0.8594 - val_loss: 0.3203 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 0s 77ms/step - loss: 0.3535 - accuracy: 0.8750 - val_loss: 0.2998 - val_accuracy: 1.0000 Epoch 21/50 4/4 [==============================] - 0s 78ms/step - loss: 0.3345 - accuracy: 0.8906 - val_loss: 0.2815 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 0s 76ms/step - loss: 0.3168 - accuracy: 0.8906 - val_loss: 0.2640 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 0s 76ms/step - loss: 0.3017 - accuracy: 0.9062 - val_loss: 0.2465 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2840 - accuracy: 0.9219 - val_loss: 0.2328 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2700 - accuracy: 0.9219 - val_loss: 0.2181 - val_accuracy: 1.0000 Epoch 26/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2566 - accuracy: 0.9219 - val_loss: 0.2053 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 0s 77ms/step - loss: 0.2445 - accuracy: 0.9375 - val_loss: 0.1935 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2332 - accuracy: 0.9375 - val_loss: 0.1839 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 0s 78ms/step - loss: 0.2227 - accuracy: 0.9375 - val_loss: 0.1734 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2145 - accuracy: 0.9375 - val_loss: 0.1630 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 0s 76ms/step - loss: 0.2047 - accuracy: 0.9375 - val_loss: 0.1564 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1971 - accuracy: 0.9375 - val_loss: 0.1525 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1894 - accuracy: 0.9531 - val_loss: 0.1464 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 0s 74ms/step - loss: 0.1825 - accuracy: 0.9531 - val_loss: 0.1407 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1771 - accuracy: 0.9531 - val_loss: 0.1330 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1704 - accuracy: 0.9531 - val_loss: 0.1288 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1647 - accuracy: 0.9531 - val_loss: 0.1237 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 0s 80ms/step - loss: 0.1603 - accuracy: 0.9531 - val_loss: 0.1221 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1551 - accuracy: 0.9688 - val_loss: 0.1177 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1509 - accuracy: 0.9688 - val_loss: 0.1136 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1466 - accuracy: 0.9688 - val_loss: 0.1110 - val_accuracy: 1.0000 Epoch 42/50 4/4 [==============================] - 0s 76ms/step - loss: 0.1426 - accuracy: 0.9688 - val_loss: 0.1083 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1386 - accuracy: 0.9688 - val_loss: 0.1050 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 0s 83ms/step - loss: 0.1362 - accuracy: 0.9688 - val_loss: 0.0989 - val_accuracy: 1.0000 Epoch 45/50 4/4 [==============================] - 0s 78ms/step - loss: 0.1324 - accuracy: 0.9688 - val_loss: 0.0978 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1290 - accuracy: 0.9688 - val_loss: 0.0964 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 0s 75ms/step - loss: 0.1265 - accuracy: 0.9688 - val_loss: 0.0929 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1234 - accuracy: 0.9688 - val_loss: 0.0923 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1213 - accuracy: 0.9688 - val_loss: 0.0903 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 0s 77ms/step - loss: 0.1182 - accuracy: 0.9688 - val_loss: 0.0885 - val_accuracy: 1.0000
Ed esplorare i risultati e l'accuratezza:
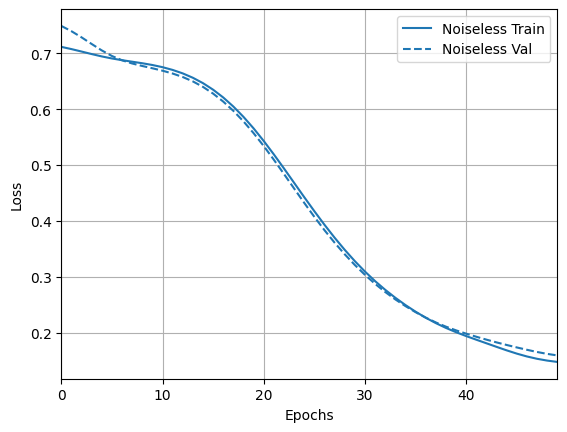
loss_plotter = tfdocs.plots.HistoryPlotter(metric = 'loss', smoothing_std=10)
loss_plotter.plot(training_histories)
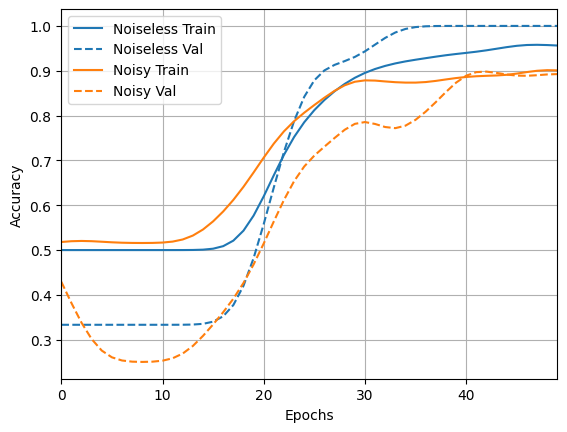
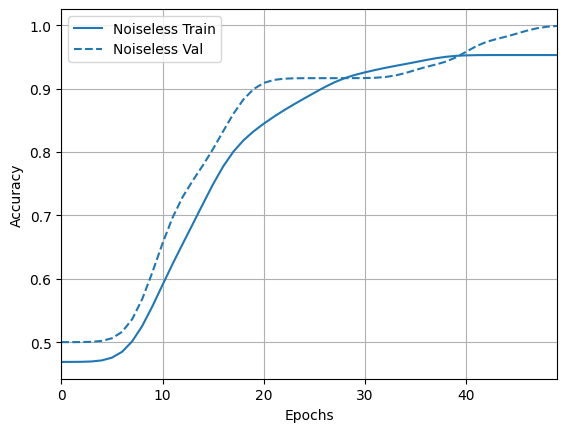
acc_plotter = tfdocs.plots.HistoryPlotter(metric = 'accuracy', smoothing_std=10)
acc_plotter.plot(training_histories)
4.2 Confronto rumoroso
Ora puoi costruire un nuovo modello con una struttura rumorosa e confrontare con quanto sopra, il codice è quasi identico:
depolarize_p = 0.001
n_epochs = 50
noisy_phase_classifier = build_keras_model(qubits, depolarize_p)
noisy_phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
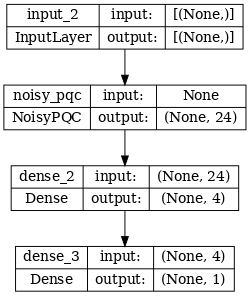
# Show the keras plot of the model
tf.keras.utils.plot_model(noisy_phase_classifier, show_shapes=True, dpi=70)
noisy_data, noisy_labels = get_data(qubits, depolarize_p)
training_histories['noisy'] = noisy_phase_classifier.fit(x=noisy_data,
y=noisy_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 8s 2s/step - loss: 0.8265 - accuracy: 0.4844 - val_loss: 0.8369 - val_accuracy: 0.4167 Epoch 2/50 4/4 [==============================] - 7s 2s/step - loss: 0.7613 - accuracy: 0.4844 - val_loss: 0.7695 - val_accuracy: 0.4167 Epoch 3/50 4/4 [==============================] - 7s 2s/step - loss: 0.7151 - accuracy: 0.4844 - val_loss: 0.7290 - val_accuracy: 0.4167 Epoch 4/50 4/4 [==============================] - 7s 2s/step - loss: 0.6915 - accuracy: 0.4844 - val_loss: 0.7014 - val_accuracy: 0.4167 Epoch 5/50 4/4 [==============================] - 7s 2s/step - loss: 0.6837 - accuracy: 0.4844 - val_loss: 0.6811 - val_accuracy: 0.4167 Epoch 6/50 4/4 [==============================] - 7s 2s/step - loss: 0.6717 - accuracy: 0.4844 - val_loss: 0.6801 - val_accuracy: 0.4167 Epoch 7/50 4/4 [==============================] - 7s 2s/step - loss: 0.6739 - accuracy: 0.4844 - val_loss: 0.6726 - val_accuracy: 0.4167 Epoch 8/50 4/4 [==============================] - 7s 2s/step - loss: 0.6713 - accuracy: 0.4844 - val_loss: 0.6661 - val_accuracy: 0.4167 Epoch 9/50 4/4 [==============================] - 7s 2s/step - loss: 0.6710 - accuracy: 0.4844 - val_loss: 0.6667 - val_accuracy: 0.4167 Epoch 10/50 4/4 [==============================] - 7s 2s/step - loss: 0.6669 - accuracy: 0.4844 - val_loss: 0.6627 - val_accuracy: 0.4167 Epoch 11/50 4/4 [==============================] - 7s 2s/step - loss: 0.6637 - accuracy: 0.4844 - val_loss: 0.6550 - val_accuracy: 0.4167 Epoch 12/50 4/4 [==============================] - 7s 2s/step - loss: 0.6616 - accuracy: 0.4844 - val_loss: 0.6593 - val_accuracy: 0.4167 Epoch 13/50 4/4 [==============================] - 7s 2s/step - loss: 0.6536 - accuracy: 0.4844 - val_loss: 0.6514 - val_accuracy: 0.4167 Epoch 14/50 4/4 [==============================] - 7s 2s/step - loss: 0.6489 - accuracy: 0.4844 - val_loss: 0.6481 - val_accuracy: 0.4167 Epoch 15/50 4/4 [==============================] - 7s 2s/step - loss: 0.6491 - accuracy: 0.4844 - val_loss: 0.6484 - val_accuracy: 0.4167 Epoch 16/50 4/4 [==============================] - 7s 2s/step - loss: 0.6389 - accuracy: 0.4844 - val_loss: 0.6396 - val_accuracy: 0.4167 Epoch 17/50 4/4 [==============================] - 7s 2s/step - loss: 0.6307 - accuracy: 0.4844 - val_loss: 0.6337 - val_accuracy: 0.4167 Epoch 18/50 4/4 [==============================] - 7s 2s/step - loss: 0.6296 - accuracy: 0.4844 - val_loss: 0.6260 - val_accuracy: 0.4167 Epoch 19/50 4/4 [==============================] - 7s 2s/step - loss: 0.6194 - accuracy: 0.4844 - val_loss: 0.6282 - val_accuracy: 0.4167 Epoch 20/50 4/4 [==============================] - 7s 2s/step - loss: 0.6095 - accuracy: 0.4844 - val_loss: 0.6138 - val_accuracy: 0.4167 Epoch 21/50 4/4 [==============================] - 7s 2s/step - loss: 0.6075 - accuracy: 0.4844 - val_loss: 0.5874 - val_accuracy: 0.4167 Epoch 22/50 4/4 [==============================] - 7s 2s/step - loss: 0.5981 - accuracy: 0.4844 - val_loss: 0.5981 - val_accuracy: 0.4167 Epoch 23/50 4/4 [==============================] - 7s 2s/step - loss: 0.5823 - accuracy: 0.4844 - val_loss: 0.5818 - val_accuracy: 0.4167 Epoch 24/50 4/4 [==============================] - 7s 2s/step - loss: 0.5768 - accuracy: 0.4844 - val_loss: 0.5617 - val_accuracy: 0.4167 Epoch 25/50 4/4 [==============================] - 7s 2s/step - loss: 0.5651 - accuracy: 0.4844 - val_loss: 0.5638 - val_accuracy: 0.4167 Epoch 26/50 4/4 [==============================] - 7s 2s/step - loss: 0.5496 - accuracy: 0.4844 - val_loss: 0.5532 - val_accuracy: 0.4167 Epoch 27/50 4/4 [==============================] - 7s 2s/step - loss: 0.5340 - accuracy: 0.5000 - val_loss: 0.5345 - val_accuracy: 0.4167 Epoch 28/50 4/4 [==============================] - 7s 2s/step - loss: 0.5297 - accuracy: 0.5156 - val_loss: 0.5308 - val_accuracy: 0.4167 Epoch 29/50 4/4 [==============================] - 7s 2s/step - loss: 0.5120 - accuracy: 0.5312 - val_loss: 0.5224 - val_accuracy: 0.5000 Epoch 30/50 4/4 [==============================] - 7s 2s/step - loss: 0.4992 - accuracy: 0.5781 - val_loss: 0.4921 - val_accuracy: 0.5833 Epoch 31/50 4/4 [==============================] - 7s 2s/step - loss: 0.4823 - accuracy: 0.5938 - val_loss: 0.4975 - val_accuracy: 0.5000 Epoch 32/50 4/4 [==============================] - 7s 2s/step - loss: 0.5025 - accuracy: 0.5781 - val_loss: 0.4814 - val_accuracy: 0.5000 Epoch 33/50 4/4 [==============================] - 7s 2s/step - loss: 0.4655 - accuracy: 0.6562 - val_loss: 0.4391 - val_accuracy: 0.6667 Epoch 34/50 4/4 [==============================] - 7s 2s/step - loss: 0.4552 - accuracy: 0.7031 - val_loss: 0.4528 - val_accuracy: 0.5833 Epoch 35/50 4/4 [==============================] - 7s 2s/step - loss: 0.4516 - accuracy: 0.6719 - val_loss: 0.3993 - val_accuracy: 0.8333 Epoch 36/50 4/4 [==============================] - 7s 2s/step - loss: 0.4320 - accuracy: 0.7656 - val_loss: 0.4225 - val_accuracy: 0.6667 Epoch 37/50 4/4 [==============================] - 7s 2s/step - loss: 0.4060 - accuracy: 0.7656 - val_loss: 0.4001 - val_accuracy: 0.9167 Epoch 38/50 4/4 [==============================] - 7s 2s/step - loss: 0.3858 - accuracy: 0.7812 - val_loss: 0.4152 - val_accuracy: 0.8333 Epoch 39/50 4/4 [==============================] - 7s 2s/step - loss: 0.3964 - accuracy: 0.7656 - val_loss: 0.3899 - val_accuracy: 0.7500 Epoch 40/50 4/4 [==============================] - 7s 2s/step - loss: 0.3640 - accuracy: 0.8125 - val_loss: 0.3689 - val_accuracy: 0.7500 Epoch 41/50 4/4 [==============================] - 7s 2s/step - loss: 0.3676 - accuracy: 0.7812 - val_loss: 0.3786 - val_accuracy: 0.7500 Epoch 42/50 4/4 [==============================] - 7s 2s/step - loss: 0.3466 - accuracy: 0.8281 - val_loss: 0.3313 - val_accuracy: 0.8333 Epoch 43/50 4/4 [==============================] - 7s 2s/step - loss: 0.3520 - accuracy: 0.8594 - val_loss: 0.3398 - val_accuracy: 0.8333 Epoch 44/50 4/4 [==============================] - 7s 2s/step - loss: 0.3402 - accuracy: 0.8438 - val_loss: 0.3135 - val_accuracy: 0.9167 Epoch 45/50 4/4 [==============================] - 7s 2s/step - loss: 0.3253 - accuracy: 0.8281 - val_loss: 0.3469 - val_accuracy: 0.8333 Epoch 46/50 4/4 [==============================] - 7s 2s/step - loss: 0.3239 - accuracy: 0.8281 - val_loss: 0.3038 - val_accuracy: 0.9167 Epoch 47/50 4/4 [==============================] - 7s 2s/step - loss: 0.2948 - accuracy: 0.8594 - val_loss: 0.3056 - val_accuracy: 0.9167 Epoch 48/50 4/4 [==============================] - 7s 2s/step - loss: 0.2972 - accuracy: 0.9219 - val_loss: 0.2699 - val_accuracy: 0.9167 Epoch 49/50 4/4 [==============================] - 7s 2s/step - loss: 0.3041 - accuracy: 0.8281 - val_loss: 0.2754 - val_accuracy: 0.9167 Epoch 50/50 4/4 [==============================] - 7s 2s/step - loss: 0.2944 - accuracy: 0.8750 - val_loss: 0.2988 - val_accuracy: 0.9167
loss_plotter.plot(training_histories)
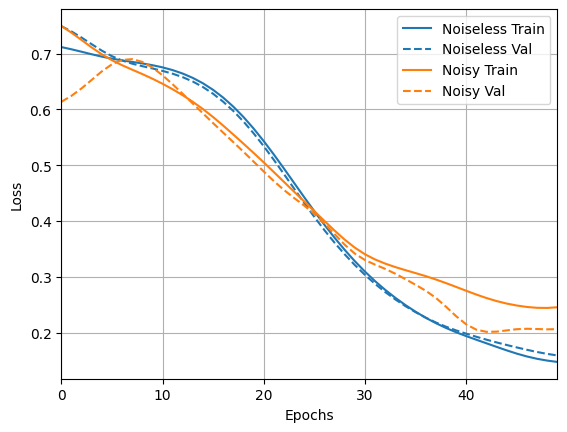
acc_plotter.plot(training_histories)