 عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
سيوضح هذا البرنامج التعليمي أفضل الممارسات الموصى بها لنماذج التدريب مع الخصوصية التفاضلية على مستوى المستخدم باستخدام Tensorflow Federated. سوف نستخدم خوارزمية DP-SGD من العبادي وآخرون، "ديب التعلم مع التفاضلية الخصوصية" المعدلة للمستوى المستخدم موانئ دبي في سياق الاتحادية في McMahan وآخرون، "نماذج التعلم تفاضلي الخاصة المتكررة اللغة" .
الخصوصية التفاضلية (DP) هي طريقة مستخدمة على نطاق واسع لإلزام وقياس تسرب الخصوصية للبيانات الحساسة عند أداء مهام التعلم. يضمن تدريب النموذج باستخدام DP على مستوى المستخدم أنه من غير المرجح أن يتعلم النموذج أي شيء مهم عن بيانات أي فرد ، ولكن لا يزال بإمكانه (نأمل!) تعلم الأنماط الموجودة في بيانات العديد من العملاء.
سنقوم بتدريب نموذج على مجموعة بيانات EMNIST الموحدة. هناك مفاضلة متأصلة بين المنفعة والخصوصية ، وقد يكون من الصعب تدريب نموذج يتمتع بخصوصية عالية يؤدي إلى جانب أحدث نموذج غير خاص. من أجل الاستفادة في هذا البرنامج التعليمي ، سوف نتدرب لـ 100 جولة فقط ، مع التضحية ببعض الجودة من أجل إظهار كيفية التدريب بخصوصية عالية. إذا استخدمنا المزيد من جولات التدريب ، فيمكننا بالتأكيد الحصول على نموذج خاص عالي الدقة إلى حد ما ، ولكن ليس بنفس مستوى النموذج الذي تم تدريبه بدون DP.
قبل أن نبدأ
أولاً ، دعونا نتأكد من توصيل الكمبيوتر الدفتري بالواجهة الخلفية التي تم تجميع المكونات ذات الصلة بها.
!pip install --quiet --upgrade tensorflow_federated_nightly
!pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
بعض الواردات التي سنحتاجها للدرس التعليمي. سوف نستخدم tensorflow_federated ، إطار مفتوح المصدر للتعلم آلة وحسابات أخرى على بيانات مركزية، فضلا عن tensorflow_privacy ، مكتبة مفتوحة المصدر لتنفيذ وتحليل الخوارزميات خاصة تفاضلي في tensorflow.
import collections
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
import tensorflow_privacy as tfp
قم بتشغيل مثال "Hello World" التالي للتأكد من إعداد بيئة TFF بشكل صحيح. إذا كان لا يعمل، يرجى الرجوع إلى تركيب دليل للتعليمات.
@tff.federated_computation
def hello_world():
return 'Hello, World!'
hello_world()
b'Hello, World!'
قم بتنزيل مجموعة بيانات EMNIST الموحدة ومعالجتها مسبقًا.
def get_emnist_dataset():
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data(
only_digits=True)
def element_fn(element):
return collections.OrderedDict(
x=tf.expand_dims(element['pixels'], -1), y=element['label'])
def preprocess_train_dataset(dataset):
# Use buffer_size same as the maximum client dataset size,
# 418 for Federated EMNIST
return (dataset.map(element_fn)
.shuffle(buffer_size=418)
.repeat(1)
.batch(32, drop_remainder=False))
def preprocess_test_dataset(dataset):
return dataset.map(element_fn).batch(128, drop_remainder=False)
emnist_train = emnist_train.preprocess(preprocess_train_dataset)
emnist_test = preprocess_test_dataset(
emnist_test.create_tf_dataset_from_all_clients())
return emnist_train, emnist_test
train_data, test_data = get_emnist_dataset()
حدد نموذجنا.
def my_model_fn():
model = tf.keras.models.Sequential([
tf.keras.layers.Reshape(input_shape=(28, 28, 1), target_shape=(28 * 28,)),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(10)])
return tff.learning.from_keras_model(
keras_model=model,
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
input_spec=test_data.element_spec,
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
تحديد حساسية ضوضاء النموذج.
للحصول على ضمانات DP على مستوى المستخدم ، يجب علينا تغيير خوارزمية المتوسطات الموحدة الأساسية بطريقتين. أولاً ، يجب قص تحديثات نموذج العملاء قبل الإرسال إلى الخادم ، مع تقييد التأثير الأقصى لأي عميل واحد. ثانيًا ، يجب أن يضيف الخادم تشويشًا كافيًا إلى مجموع تحديثات المستخدم قبل حساب المتوسط لإخفاء تأثير العميل الأسوأ.
لقطة، ونحن نستخدم طريقة لقطة التكيف من أندرو وآخرون. 2021، تفاضلي التعلم الخاصة على التكيف مع قطة ، لذلك لا يحتاج القاعدة لقطة ليتم تعيينها بشكل صريح.
ستؤدي إضافة الضوضاء بشكل عام إلى إضعاف فائدة النموذج ، ولكن يمكننا التحكم في مقدار الضوضاء في متوسط التحديث في كل جولة بمقبضين: الانحراف المعياري للضوضاء الغوسية المضافة إلى المجموع ، وعدد العملاء في معدل. ستتمثل استراتيجيتنا أولاً في تحديد مقدار الضوضاء التي يمكن أن يتحملها النموذج مع عدد صغير نسبيًا من العملاء في كل جولة مع خسارة مقبولة للنموذج. ثم لتدريب النموذج النهائي ، يمكننا زيادة مقدار الضوضاء في المجموع ، مع زيادة عدد العملاء بشكل متناسب في كل جولة (بافتراض أن مجموعة البيانات كبيرة بما يكفي لدعم هذا العدد الكبير من العملاء في كل جولة). من غير المحتمل أن يؤثر هذا بشكل كبير على جودة النموذج ، لأن التأثير الوحيد هو تقليل التباين بسبب أخذ عينات العميل (في الواقع سوف نتحقق من أنه ليس كذلك في حالتنا).
تحقيقا لهذه الغاية ، نقوم أولا بتدريب سلسلة من العارضات مع 50 عميل في كل جولة ، مع كميات متزايدة من الضوضاء. على وجه التحديد ، نقوم بزيادة "معدل الضجيج" وهو نسبة الانحراف المعياري للضوضاء إلى معيار القطع. نظرًا لأننا نستخدم القص التكيفي ، فهذا يعني أن الحجم الفعلي للضوضاء يتغير من جولة إلى أخرى.
# Run five clients per thread. Increase this if your runtime is running out of
# memory. Decrease it if you have the resources and want to speed up execution.
tff.backends.native.set_local_python_execution_context(clients_per_thread=5)
total_clients = len(train_data.client_ids)
def train(rounds, noise_multiplier, clients_per_round, data_frame):
# Using the `dp_aggregator` here turns on differential privacy with adaptive
# clipping.
aggregation_factory = tff.learning.model_update_aggregator.dp_aggregator(
noise_multiplier, clients_per_round)
# We use Poisson subsampling which gives slightly tighter privacy guarantees
# compared to having a fixed number of clients per round. The actual number of
# clients per round is stochastic with mean clients_per_round.
sampling_prob = clients_per_round / total_clients
# Build a federated averaging process.
# Typically a non-adaptive server optimizer is used because the noise in the
# updates can cause the second moment accumulators to become very large
# prematurely.
learning_process = tff.learning.build_federated_averaging_process(
my_model_fn,
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.01),
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0, momentum=0.9),
model_update_aggregation_factory=aggregation_factory)
eval_process = tff.learning.build_federated_evaluation(my_model_fn)
# Training loop.
state = learning_process.initialize()
for round in range(rounds):
if round % 5 == 0:
metrics = eval_process(state.model, [test_data])['eval']
if round < 25 or round % 25 == 0:
print(f'Round {round:3d}: {metrics}')
data_frame = data_frame.append({'Round': round,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
# Sample clients for a round. Note that if your dataset is large and
# sampling_prob is small, it would be faster to use gap sampling.
x = np.random.uniform(size=total_clients)
sampled_clients = [
train_data.client_ids[i] for i in range(total_clients)
if x[i] < sampling_prob]
sampled_train_data = [
train_data.create_tf_dataset_for_client(client)
for client in sampled_clients]
# Use selected clients for update.
state, metrics = learning_process.next(state, sampled_train_data)
metrics = eval_process(state.model, [test_data])['eval']
print(f'Round {rounds:3d}: {metrics}')
data_frame = data_frame.append({'Round': rounds,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
return data_frame
data_frame = pd.DataFrame()
rounds = 100
clients_per_round = 50
for noise_multiplier in [0.0, 0.5, 0.75, 1.0]:
print(f'Starting training with noise multiplier: {noise_multiplier}')
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
print()
Starting training with noise multiplier: 0.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.112289384), ('loss', 2.5190482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.19075724), ('loss', 2.2449977)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.18115693), ('loss', 2.163907)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49970612), ('loss', 2.01017)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5333317), ('loss', 1.8350543)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.5828517), ('loss', 1.6551636)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7352077), ('loss', 0.8700141)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7769152), ('loss', 0.6992781)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.8049814), ('loss', 0.62453026)])
Starting training with noise multiplier: 0.5
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.09526841), ('loss', 2.4332638)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.20128821), ('loss', 2.2664592)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.35472178), ('loss', 2.130336)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.5480995), ('loss', 1.9713942)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.42246276), ('loss', 1.8045483)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.624902), ('loss', 1.4785467)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7265625), ('loss', 0.85801566)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.77720904), ('loss', 0.70615387)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7702537), ('loss', 0.72331005)])
Starting training with noise multiplier: 0.75
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.098672606), ('loss', 2.422002)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.11794671), ('loss', 2.2227976)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.3208513), ('loss', 2.083766)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49752644), ('loss', 1.8728142)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5816761), ('loss', 1.6084186)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.62896746), ('loss', 1.378527)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.73153406), ('loss', 0.8705139)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7789724), ('loss', 0.7113147)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.70944357), ('loss', 0.89495045)])
Starting training with noise multiplier: 1.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.12002841), ('loss', 2.60482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.104574844), ('loss', 2.3388205)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.29966694), ('loss', 2.089262)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.4067398), ('loss', 1.9109797)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5123677), ('loss', 1.6472703)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.56416535), ('loss', 1.4362282)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.62323666), ('loss', 1.1682972)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.55968356), ('loss', 1.4779186)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.382837), ('loss', 1.9680436)])
الآن يمكننا تصور دقة مجموعة التقييم وفقدان تلك العمليات.
import matplotlib.pyplot as plt
import seaborn as sns
def make_plot(data_frame):
plt.figure(figsize=(15, 5))
dff = data_frame.rename(
columns={'sparse_categorical_accuracy': 'Accuracy', 'loss': 'Loss'})
plt.subplot(121)
sns.lineplot(data=dff, x='Round', y='Accuracy', hue='NoiseMultiplier', palette='dark')
plt.subplot(122)
sns.lineplot(data=dff, x='Round', y='Loss', hue='NoiseMultiplier', palette='dark')
make_plot(data_frame)
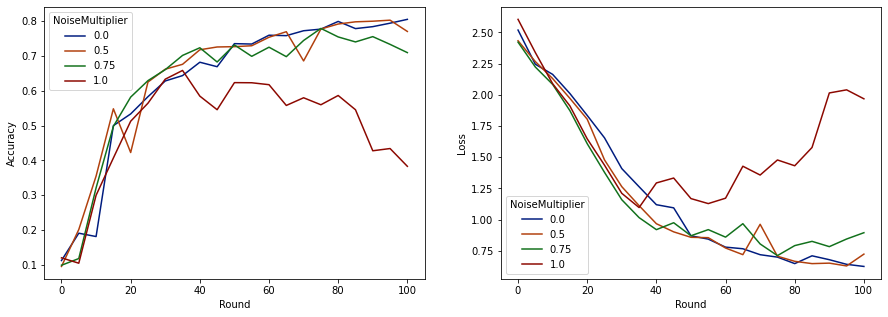
يبدو أنه مع وجود 50 عميلًا متوقعًا في كل جولة ، يمكن لهذا النموذج تحمل مضاعف ضوضاء يصل إلى 0.5 دون الإضرار بجودة النموذج. يبدو أن مضاعف الضوضاء البالغ 0.75 يسبب القليل من تدهور النموذج ، و 1.0 يجعل النموذج يتباعد.
عادة ما يكون هناك مفاضلة بين جودة النموذج والخصوصية. كلما زادت الضوضاء التي نستخدمها ، زادت الخصوصية التي نحصل عليها لنفس القدر من وقت التدريب وعدد العملاء. بالمقابل ، مع وجود ضوضاء أقل ، قد يكون لدينا نموذج أكثر دقة ، ولكن سيتعين علينا التدريب مع المزيد من العملاء في كل جولة للوصول إلى مستوى الخصوصية المستهدف.
من خلال التجربة أعلاه ، قد نقرر أن المقدار الصغير من تدهور النموذج عند 0.75 مقبول لتدريب النموذج النهائي بشكل أسرع ، لكن دعنا نفترض أننا نريد مطابقة أداء نموذج مضاعف الضوضاء 0.5.
الآن يمكننا استخدام وظائف tensorflow_privacy لتحديد عدد العملاء المتوقعين في كل جولة سنحتاجه للحصول على خصوصية مقبولة. الممارسة القياسية هي اختيار دلتا أصغر إلى حد ما من واحدة على عدد السجلات في مجموعة البيانات. تضم مجموعة البيانات هذه 3383 مستخدمًا تدريبًا إجمالاً ، لذلك دعونا نهدف إلى (2 ، 1e-5) -DP.
نحن نستخدم بحثًا ثنائيًا بسيطًا على عدد العملاء في كل جولة. ويستند ظيفة tensorflow_privacy نستخدمها لتقدير إبسيلون على وانغ وآخرون. (2018) و ميرونوف وآخرون. (2019) .
rdp_orders = ([1.25, 1.5, 1.75, 2., 2.25, 2.5, 3., 3.5, 4., 4.5] +
list(range(5, 64)) + [128, 256, 512])
total_clients = 3383
base_noise_multiplier = 0.5
base_clients_per_round = 50
target_delta = 1e-5
target_eps = 2
def get_epsilon(clients_per_round):
# If we use this number of clients per round and proportionally
# scale up the noise multiplier, what epsilon do we achieve?
q = clients_per_round / total_clients
noise_multiplier = base_noise_multiplier
noise_multiplier *= clients_per_round / base_clients_per_round
rdp = tfp.compute_rdp(
q, noise_multiplier=noise_multiplier, steps=rounds, orders=rdp_orders)
eps, _, _ = tfp.get_privacy_spent(rdp_orders, rdp, target_delta=target_delta)
return clients_per_round, eps, noise_multiplier
def find_needed_clients_per_round():
hi = get_epsilon(base_clients_per_round)
if hi[1] < target_eps:
return hi
# Grow interval exponentially until target_eps is exceeded.
while True:
lo = hi
hi = get_epsilon(2 * lo[0])
if hi[1] < target_eps:
break
# Binary search.
while hi[0] - lo[0] > 1:
mid = get_epsilon((lo[0] + hi[0]) // 2)
if mid[1] > target_eps:
lo = mid
else:
hi = mid
return hi
clients_per_round, _, noise_multiplier = find_needed_clients_per_round()
print(f'To get ({target_eps}, {target_delta})-DP, use {clients_per_round} '
f'clients with noise multiplier {noise_multiplier}.')
To get (2, 1e-05)-DP, use 120 clients with noise multiplier 1.2.
الآن يمكننا تدريب نموذجنا الخاص النهائي للإفراج.
rounds = 100
noise_multiplier = 1.2
clients_per_round = 120
data_frame = pd.DataFrame()
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
make_plot(data_frame)
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.08260678), ('loss', 2.6334999)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.1492212), ('loss', 2.259542)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.28847474), ('loss', 2.155699)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.3989518), ('loss', 2.0156953)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5086697), ('loss', 1.8261365)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.6204692), ('loss', 1.5602393)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.70008814), ('loss', 0.91155165)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.78421336), ('loss', 0.6820159)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7955525), ('loss', 0.6585961)])
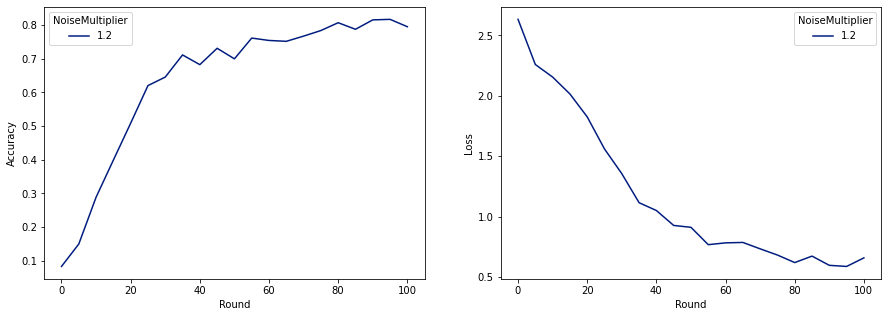
كما نرى ، فإن النموذج النهائي له خسارة ودقة مماثلة للنموذج المدرب بدون ضوضاء ، لكن هذا النموذج يرضي (2 ، 1e-5) -DP.
