 Zobacz na TensorFlow.org |  Uruchom w Google Colab |  Wyświetl źródło na GitHub |  Pobierz notatnik |
import tensorflow as tf
import numpy as np
Tensory to wielowymiarowe tablice o jednorodnym typie (zwanym dtype ). Wszystkie obsługiwane dtypestf.dtypes.DType można zobaczyć dtypes adresemtf.dtypes.DType .
Jeśli znasz NumPy , tensory są (w pewnym np.arrays ) jak np.arrays . np.arrays .
Wszystkie tensory są niezmienne, tak jak liczby i ciągi znaków w Pythonie: nigdy nie można zaktualizować zawartości tensora, wystarczy utworzyć nowy.
Podstawy
Stwórzmy kilka podstawowych tensorów.
Oto tensor „skalarny” lub „rangi-0”. Skalar zawiera pojedynczą wartość i nie zawiera „osi”.
# This will be an int32 tensor by default; see "dtypes" below.
rank_0_tensor = tf.constant(4)
print(rank_0_tensor)
tf.Tensor(4, shape=(), dtype=int32)
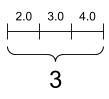
Tensor typu „vector” lub „rank-1” jest jak lista wartości. Wektor ma jedną oś:
# Let's make this a float tensor.
rank_1_tensor = tf.constant([2.0, 3.0, 4.0])
print(rank_1_tensor)
tf.Tensor([2. 3. 4.], shape=(3,), dtype=float32)
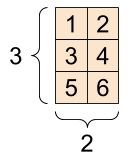
Tensor „macierzowy” lub „rząd 2” ma dwie osie:
# If you want to be specific, you can set the dtype (see below) at creation time
rank_2_tensor = tf.constant([[1, 2],
[3, 4],
[5, 6]], dtype=tf.float16)
print(rank_2_tensor)
tf.Tensor( [[1. 2.] [3. 4.] [5. 6.]], shape=(3, 2), dtype=float16)
Skalar, kształt: [] | Wektor, kształt: [3] | Macierz, kształt: [3, 2] |
|---|---|---|
 |  |  |
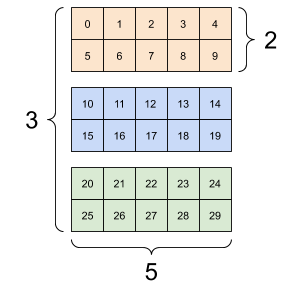
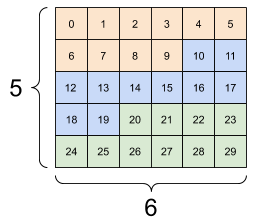
Tensory mogą mieć więcej osi; oto tensor z trzema osiami:
# There can be an arbitrary number of
# axes (sometimes called "dimensions")
rank_3_tensor = tf.constant([
[[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]],
[[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]],
[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29]],])
print(rank_3_tensor)
tf.Tensor( [[[ 0 1 2 3 4] [ 5 6 7 8 9]] [[10 11 12 13 14] [15 16 17 18 19]] [[20 21 22 23 24] [25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)
Istnieje wiele sposobów wizualizacji tensora z więcej niż dwiema osiami.
Tensor 3-osiowy, kształt: [3, 2, 5] | ||
|---|---|---|
 |  |  |
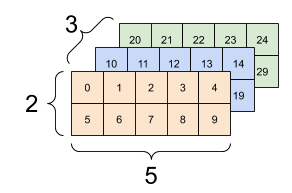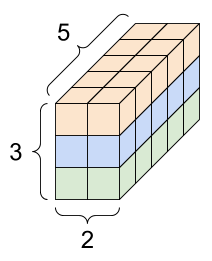Możesz przekonwertować tensor na tablicę NumPy za pomocą np.array lub tensor.numpy :
np.array(rank_2_tensor)
array([[1., 2.],
[3., 4.],
[5., 6.]], dtype=float16)
rank_2_tensor.numpy()
array([[1., 2.],
[3., 4.],
[5., 6.]], dtype=float16)
Tensory często zawierają liczby zmiennoprzecinkowe i liczby całkowite, ale mają wiele innych typów, w tym:
- Liczby zespolone
- smyczki
tf.Tensor klasa tf.Tensor wymaga, aby tensory były „prostokątne” - to znaczy wzdłuż każdej osi każdy element ma ten sam rozmiar. Istnieją jednak specjalistyczne typy tensorów, które mogą obsługiwać różne kształty:
- Ragged tensors (patrz RaggedTensor poniżej)
- Rzadkie tensory (patrz SparseTensor poniżej)
Możesz wykonywać podstawowe obliczenia matematyczne na tensorach, w tym dodawanie, mnożenie według elementów i mnożenie macierzy.
a = tf.constant([[1, 2],
[3, 4]])
b = tf.constant([[1, 1],
[1, 1]]) # Could have also said `tf.ones([2,2])`
print(tf.add(a, b), "\n")
print(tf.multiply(a, b), "\n")
print(tf.matmul(a, b), "\n")
tf.Tensor( [[2 3] [4 5]], shape=(2, 2), dtype=int32) tf.Tensor( [[1 2] [3 4]], shape=(2, 2), dtype=int32) tf.Tensor( [[3 3] [7 7]], shape=(2, 2), dtype=int32)
print(a + b, "\n") # element-wise addition
print(a * b, "\n") # element-wise multiplication
print(a @ b, "\n") # matrix multiplication
tf.Tensor( [[2 3] [4 5]], shape=(2, 2), dtype=int32) tf.Tensor( [[1 2] [3 4]], shape=(2, 2), dtype=int32) tf.Tensor( [[3 3] [7 7]], shape=(2, 2), dtype=int32)
Tensory są używane we wszystkich rodzajach operacji (ops).
c = tf.constant([[4.0, 5.0], [10.0, 1.0]])
# Find the largest value
print(tf.reduce_max(c))
# Find the index of the largest value
print(tf.argmax(c))
# Compute the softmax
print(tf.nn.softmax(c))
tf.Tensor(10.0, shape=(), dtype=float32) tf.Tensor([1 0], shape=(2,), dtype=int64) tf.Tensor( [[2.6894143e-01 7.3105854e-01] [9.9987662e-01 1.2339458e-04]], shape=(2, 2), dtype=float32)
O kształtach
Tensory mają kształty. Niektóre słownictwo:
- Kształt : długość (liczba elementów) każdej z osi tensora.
- Ranga : Liczba osi tensora. Skalar ma rangę 0, wektor ma rangę 1, a macierz ma rangę 2.
- Oś lub wymiar : określony wymiar tensora.
- Rozmiar : całkowita liczba elementów w tensorze, wektorze kształtu produktu.
tf.TensorShape i obiekty tf.TensorShape mają wygodne właściwości umożliwiające dostęp do nich:
rank_4_tensor = tf.zeros([3, 2, 4, 5])
Tensor rzędu 4, kształt: [3, 2, 4, 5] | |
|---|---|
 |  |
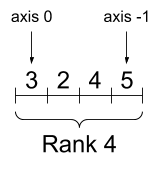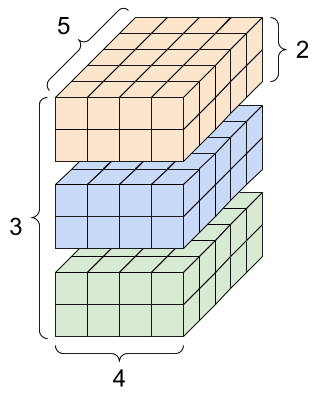print("Type of every element:", rank_4_tensor.dtype)
print("Number of axes:", rank_4_tensor.ndim)
print("Shape of tensor:", rank_4_tensor.shape)
print("Elements along axis 0 of tensor:", rank_4_tensor.shape[0])
print("Elements along the last axis of tensor:", rank_4_tensor.shape[-1])
print("Total number of elements (3*2*4*5): ", tf.size(rank_4_tensor).numpy())
Type of every element: <dtype: 'float32'> Number of axes: 4 Shape of tensor: (3, 2, 4, 5) Elements along axis 0 of tensor: 3 Elements along the last axis of tensor: 5 Total number of elements (3*2*4*5): 120
Chociaż indeksy często odnoszą się do osi, należy zawsze śledzić znaczenie każdego z nich. Często osie są uporządkowane w kolejności od globalnej do lokalnej: najpierw oś wsadowa, następnie wymiary przestrzenne, a na końcu cechy dla każdej lokalizacji. W ten sposób wektory cech są ciągłymi obszarami pamięci.
| Typowa kolejność osi |
|---|
 |
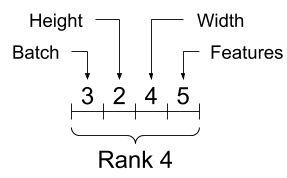Indeksowanie
Indeksowanie jednoosiowe
TensorFlow przestrzega standardowych reguł indeksowania Pythona, podobnych do indeksowania listy lub ciągu znaków w Pythonie , oraz podstawowych reguł indeksowania NumPy.
- indeksy zaczynają się od
0 - indeksy ujemne liczą się wstecz od końca
- dwukropki,
:, są używane do wycinków:start:stop:step
rank_1_tensor = tf.constant([0, 1, 1, 2, 3, 5, 8, 13, 21, 34])
print(rank_1_tensor.numpy())
[ 0 1 1 2 3 5 8 13 21 34]
Indeksowanie skalarem usuwa oś:
print("First:", rank_1_tensor[0].numpy())
print("Second:", rank_1_tensor[1].numpy())
print("Last:", rank_1_tensor[-1].numpy())
First: 0 Second: 1 Last: 34
Indeksowanie za pomocą : plaster zachowuje oś:
print("Everything:", rank_1_tensor[:].numpy())
print("Before 4:", rank_1_tensor[:4].numpy())
print("From 4 to the end:", rank_1_tensor[4:].numpy())
print("From 2, before 7:", rank_1_tensor[2:7].numpy())
print("Every other item:", rank_1_tensor[::2].numpy())
print("Reversed:", rank_1_tensor[::-1].numpy())
Everything: [ 0 1 1 2 3 5 8 13 21 34] Before 4: [0 1 1 2] From 4 to the end: [ 3 5 8 13 21 34] From 2, before 7: [1 2 3 5 8] Every other item: [ 0 1 3 8 21] Reversed: [34 21 13 8 5 3 2 1 1 0]
Indeksowanie wieloosiowe
Tensory wyższego rzędu są indeksowane przez przekazywanie wielu indeksów.
Dokładnie te same zasady, co w przypadku pojedynczej osi, mają zastosowanie do każdej osi niezależnie.
print(rank_2_tensor.numpy())
[[1. 2.] [3. 4.] [5. 6.]]
Przekazując liczbę całkowitą dla każdego indeksu, wynikiem jest wartość skalarna.
# Pull out a single value from a 2-rank tensor
print(rank_2_tensor[1, 1].numpy())
4.0
Indeksowanie można indeksować przy użyciu dowolnej kombinacji liczb całkowitych i wycinków:
# Get row and column tensors
print("Second row:", rank_2_tensor[1, :].numpy())
print("Second column:", rank_2_tensor[:, 1].numpy())
print("Last row:", rank_2_tensor[-1, :].numpy())
print("First item in last column:", rank_2_tensor[0, -1].numpy())
print("Skip the first row:")
print(rank_2_tensor[1:, :].numpy(), "\n")
Second row: [3. 4.] Second column: [2. 4. 6.] Last row: [5. 6.] First item in last column: 2.0 Skip the first row: [[3. 4.] [5. 6.]]
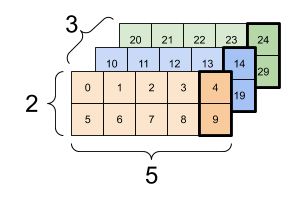
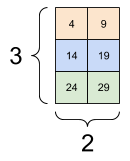
Oto przykład z tensorem 3-osiowym:
print(rank_3_tensor[:, :, 4])
tf.Tensor( [[ 4 9] [14 19] [24 29]], shape=(3, 2), dtype=int32)
| Wybór ostatniej funkcji we wszystkich lokalizacjach w każdym przykładzie w partii | |
|---|---|
 |  |
Manipulowanie kształtami
Przekształcenie tensora jest bardzo przydatne.
# Shape returns a `TensorShape` object that shows the size along each axis
x = tf.constant([[1], [2], [3]])
print(x.shape)
(3, 1)
# You can convert this object into a Python list, too
print(x.shape.as_list())
[3, 1]
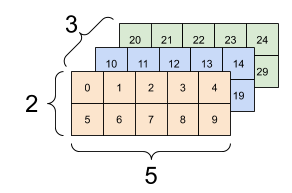
Możesz przekształcić tensor w nowy kształt. Operacja tf.reshape jest szybka i tania, ponieważ podstawowe dane nie muszą być powielane.
# You can reshape a tensor to a new shape.
# Note that you're passing in a list
reshaped = tf.reshape(x, [1, 3])
print(x.shape)
print(reshaped.shape)
(3, 1) (1, 3)
Dane zachowują swój układ w pamięci i tworzony jest nowy tensor o żądanym kształcie wskazującym na te same dane. TensorFlow korzysta z porządkowania pamięci w stylu „row-major”, gdzie inkrementacja indeksu znajdującego się najbardziej po prawej stronie odpowiada pojedynczemu krokowi w pamięci.
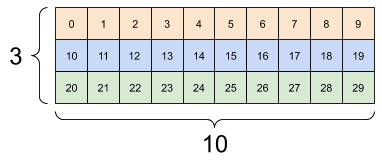
print(rank_3_tensor)
tf.Tensor( [[[ 0 1 2 3 4] [ 5 6 7 8 9]] [[10 11 12 13 14] [15 16 17 18 19]] [[20 21 22 23 24] [25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)
Jeśli spłaszczysz tensor, możesz zobaczyć, w jakiej kolejności jest on ułożony w pamięci.
# A `-1` passed in the `shape` argument says "Whatever fits".
print(tf.reshape(rank_3_tensor, [-1]))
tf.Tensor( [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29], shape=(30,), dtype=int32)
Zazwyczaj jedynym rozsądnym zastosowaniem tf.reshape jest łączenie lub dzielenie sąsiednich osi (lub dodawanie / usuwanie 1 s).
W przypadku tego tensora 3x2x5 zmiana kształtu na (3x2) x5 lub 3x (2x5) jest rozsądnym rozwiązaniem, ponieważ plasterki się nie mieszają:
print(tf.reshape(rank_3_tensor, [3*2, 5]), "\n")
print(tf.reshape(rank_3_tensor, [3, -1]))
tf.Tensor( [[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14] [15 16 17 18 19] [20 21 22 23 24] [25 26 27 28 29]], shape=(6, 5), dtype=int32) tf.Tensor( [[ 0 1 2 3 4 5 6 7 8 9] [10 11 12 13 14 15 16 17 18 19] [20 21 22 23 24 25 26 27 28 29]], shape=(3, 10), dtype=int32)
| Kilka dobrych zmian. | ||
|---|---|---|
 |  |  |
Przekształcanie będzie „działało” dla każdego nowego kształtu z tą samą całkowitą liczbą elementów, ale nie przyniesie nic pożytecznego, jeśli nie będziesz przestrzegać kolejności osi.
Zamiana osi w tf.reshape nie działa; potrzebujesz do tego tf.transpose .
# Bad examples: don't do this
# You can't reorder axes with reshape.
print(tf.reshape(rank_3_tensor, [2, 3, 5]), "\n")
# This is a mess
print(tf.reshape(rank_3_tensor, [5, 6]), "\n")
# This doesn't work at all
try:
tf.reshape(rank_3_tensor, [7, -1])
except Exception as e:
print(f"{type(e).__name__}: {e}")
tf.Tensor( [[[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14]] [[15 16 17 18 19] [20 21 22 23 24] [25 26 27 28 29]]], shape=(2, 3, 5), dtype=int32) tf.Tensor( [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23] [24 25 26 27 28 29]], shape=(5, 6), dtype=int32) InvalidArgumentError: Input to reshape is a tensor with 30 values, but the requested shape requires a multiple of 7 [Op:Reshape]
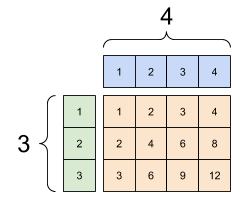
| Kilka złych zmian. | ||
|---|---|---|
 |  |  |
Możesz napotkać nie do końca określone kształty. Albo kształt zawiera None (długość osi jest nieznana), albo cały kształt jest None (ranga tensora jest nieznana).
Z wyjątkiem tf.RaggedTensor takie kształty będą występować tylko w kontekście symbolicznych interfejsów API budujących wykresy TensorFlow:
Więcej o DTypes
Sprawdzamy tf.Tensor typu danych użyć „sTensor.dtype nieruchomości.
Podczas tworzenia tf.Tensor z obiektu Pythona możesz opcjonalnie określić typ danych.
Jeśli tego nie zrobisz, TensorFlow wybierze typ danych, który może reprezentować Twoje dane. TensorFlow konwertuje liczby całkowite Pythona na tf.int32 a liczby zmiennoprzecinkowe Pythona na tf.float32 . W przeciwnym razie TensorFlow korzysta z tych samych reguł, których używa NumPy podczas konwersji na tablice.
Możesz przesyłać z typu na tekst.
the_f64_tensor = tf.constant([2.2, 3.3, 4.4], dtype=tf.float64)
the_f16_tensor = tf.cast(the_f64_tensor, dtype=tf.float16)
# Now, cast to an uint8 and lose the decimal precision
the_u8_tensor = tf.cast(the_f16_tensor, dtype=tf.uint8)
print(the_u8_tensor)
tf.Tensor([2 3 4], shape=(3,), dtype=uint8)
Nadawanie
Nadawanie to koncepcja zapożyczona z równoważnej funkcji w NumPy . Krótko mówiąc, w pewnych warunkach mniejsze tensory są „rozciągane” automatycznie, aby dopasować większe tensory podczas wykonywania na nich połączonych operacji.
Najprostszym i najczęstszym przypadkiem jest próba pomnożenia lub dodania tensora do skalara. W takim przypadku nadawany jest skalar, który ma taki sam kształt jak drugi argument.
x = tf.constant([1, 2, 3])
y = tf.constant(2)
z = tf.constant([2, 2, 2])
# All of these are the same computation
print(tf.multiply(x, 2))
print(x * y)
print(x * z)
tf.Tensor([2 4 6], shape=(3,), dtype=int32) tf.Tensor([2 4 6], shape=(3,), dtype=int32) tf.Tensor([2 4 6], shape=(3,), dtype=int32)
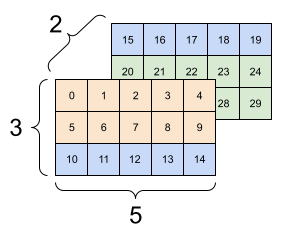
Podobnie osie o długości 1 można rozciągnąć, aby dopasować je do innych argumentów. Oba argumenty można rozciągnąć w tym samym obliczeniu.
W tym przypadku macierz 3x1 jest mnożona elementarnie przez macierz 1x4, aby otrzymać macierz 3x4. Zwróć uwagę, że wiodąca 1 jest opcjonalna: kształt y to [4] .
# These are the same computations
x = tf.reshape(x,[3,1])
y = tf.range(1, 5)
print(x, "\n")
print(y, "\n")
print(tf.multiply(x, y))
tf.Tensor( [[1] [2] [3]], shape=(3, 1), dtype=int32) tf.Tensor([1 2 3 4], shape=(4,), dtype=int32) tf.Tensor( [[ 1 2 3 4] [ 2 4 6 8] [ 3 6 9 12]], shape=(3, 4), dtype=int32)
Rozgłoszony dodatek: a [3, 1] razy a [1, 4] daje [3,4] |
|---|
 |
Oto ta sama operacja bez nadawania:
x_stretch = tf.constant([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
y_stretch = tf.constant([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
print(x_stretch * y_stretch) # Again, operator overloading
tf.Tensor( [[ 1 2 3 4] [ 2 4 6 8] [ 3 6 9 12]], shape=(3, 4), dtype=int32)
W większości przypadków nadawanie jest efektywne zarówno pod względem czasu, jak i przestrzeni, ponieważ operacja nadawania nigdy nie materializuje rozszerzonych tensorów w pamięci.
Widzisz, jak wygląda nadawanie, używająctf.broadcast_to .
print(tf.broadcast_to(tf.constant([1, 2, 3]), [3, 3]))
tf.Tensor( [[1 2 3] [1 2 3] [1 2 3]], shape=(3, 3), dtype=int32)
W przeciwieństwie do operacji matematycznej, na przykład, broadcast_to nie robi nic specjalnego, aby oszczędzać pamięć. Tutaj materializujesz tensor.
Może się to jeszcze bardziej skomplikować. Ta sekcja książki Jake'a VanderPlasa Python Data Science Handbook pokazuje więcej sztuczek nadawczych (ponownie w NumPy).
tf.convert_to_tensor
Większość tf.matmul , takich jak tf.matmul i tf.reshape przyjmuje argumenty klasy tf.Tensor . Jednak zauważysz, że w powyższym przypadku obiekty Pythona w kształcie tensorów są akceptowane.
Większość operacji, ale nie wszystkie, wywołuje convert_to_tensor w przypadku argumentów innych niż tensor. Istnieje rejestr konwersji, a większość klas obiektów, takich jak ndarray , TensorShape , listy Pythona i tf.Variable zostanie przekonwertowanych automatycznie.
Zobacz tf.register_tensor_conversion_function aby uzyskać więcej informacji, a jeśli masz własny typ, chcesz automatycznie przekształcić go w tensor.
Poszarpane tensory
Tensor ze zmienną liczbą elementów wzdłuż jakiejś osi nazywany jest „postrzępionym”. Użyj tf.ragged.RaggedTensor dla poszarpanych danych.
Na przykład nie można tego przedstawić jako zwykły tensor:
tf.RaggedTensor , kształt: [4, None] |
|---|
 |
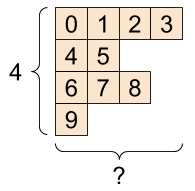ragged_list = [
[0, 1, 2, 3],
[4, 5],
[6, 7, 8],
[9]]
try:
tensor = tf.constant(ragged_list)
except Exception as e:
print(f"{type(e).__name__}: {e}")
ValueError: Can't convert non-rectangular Python sequence to Tensor.
Zamiast tego utwórztf.RaggedTensor za pomocą tf.ragged.constant :
ragged_tensor = tf.ragged.constant(ragged_list)
print(ragged_tensor)
<tf.RaggedTensor [[0, 1, 2, 3], [4, 5], [6, 7, 8], [9]]>
Kształttf.RaggedTensor będzie zawierał kilka osi o nieznanych długościach:
print(ragged_tensor.shape)
(4, None)
Napinacze strun
tf.string jest dtype , to znaczy można reprezentować dane jako ciągi (o zmiennej długości tablicami bajtów) w tensorów.
Łańcuchy są niepodzielne i nie mogą być indeksowane w taki sam sposób, jak napisy w Pythonie. Długość struny nie jest jedną z osi tensora. Zobacz tf.strings aby tf.strings funkcje, tf.strings można nimi manipulować.
Oto skalarny tensor łańcucha:
# Tensors can be strings, too here is a scalar string.
scalar_string_tensor = tf.constant("Gray wolf")
print(scalar_string_tensor)
tf.Tensor(b'Gray wolf', shape=(), dtype=string)
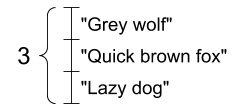
Oraz wektor ciągów:
Wektor strun, kształt: [3,] |
|---|
 |
# If you have three string tensors of different lengths, this is OK.
tensor_of_strings = tf.constant(["Gray wolf",
"Quick brown fox",
"Lazy dog"])
# Note that the shape is (3,). The string length is not included.
print(tensor_of_strings)
tf.Tensor([b'Gray wolf' b'Quick brown fox' b'Lazy dog'], shape=(3,), dtype=string)
Na powyższym wydruku przedrostek b wskazuje, że tf.string nie jest ciągiem znaków Unicode, ale ciągiem bajtów. Zobacz samouczek Unicode, aby uzyskać więcej informacji na temat pracy z tekstem Unicode w TensorFlow.
Jeśli przekazujesz znaki Unicode, są one zakodowane w formacie UTF-8.
tf.constant("🥳👍")
<tf.Tensor: shape=(), dtype=string, numpy=b'\xf0\x9f\xa5\xb3\xf0\x9f\x91\x8d'>
Niektóre podstawowe funkcje z łańcuchami można znaleźć w tf.strings , w tym tf.strings.split .
# You can use split to split a string into a set of tensors
print(tf.strings.split(scalar_string_tensor, sep=" "))
tf.Tensor([b'Gray' b'wolf'], shape=(2,), dtype=string)
# ...but it turns into a `RaggedTensor` if you split up a tensor of strings,
# as each string might be split into a different number of parts.
print(tf.strings.split(tensor_of_strings))
<tf.RaggedTensor [[b'Gray', b'wolf'], [b'Quick', b'brown', b'fox'], [b'Lazy', b'dog']]>
Trzy struny podzielone, kształt: [3, None] |
|---|
 |
Oraz tf.string.to_number :
text = tf.constant("1 10 100")
print(tf.strings.to_number(tf.strings.split(text, " ")))
tf.Tensor([ 1. 10. 100.], shape=(3,), dtype=float32)
Chociaż nie można użyć tf.cast do przekształcenia tensora łańcucha w liczby, można go przekonwertować na bajty, a następnie na liczby.
byte_strings = tf.strings.bytes_split(tf.constant("Duck"))
byte_ints = tf.io.decode_raw(tf.constant("Duck"), tf.uint8)
print("Byte strings:", byte_strings)
print("Bytes:", byte_ints)
Byte strings: tf.Tensor([b'D' b'u' b'c' b'k'], shape=(4,), dtype=string) Bytes: tf.Tensor([ 68 117 99 107], shape=(4,), dtype=uint8)
# Or split it up as unicode and then decode it
unicode_bytes = tf.constant("アヒル 🦆")
unicode_char_bytes = tf.strings.unicode_split(unicode_bytes, "UTF-8")
unicode_values = tf.strings.unicode_decode(unicode_bytes, "UTF-8")
print("\nUnicode bytes:", unicode_bytes)
print("\nUnicode chars:", unicode_char_bytes)
print("\nUnicode values:", unicode_values)
Unicode bytes: tf.Tensor(b'\xe3\x82\xa2\xe3\x83\x92\xe3\x83\xab \xf0\x9f\xa6\x86', shape=(), dtype=string) Unicode chars: tf.Tensor([b'\xe3\x82\xa2' b'\xe3\x83\x92' b'\xe3\x83\xab' b' ' b'\xf0\x9f\xa6\x86'], shape=(5,), dtype=string) Unicode values: tf.Tensor([ 12450 12498 12523 32 129414], shape=(5,), dtype=int32)
Typ tf.string jest używany dla wszystkich nieprzetworzonych danych bajtów w TensorFlow. Moduł tf.io zawiera funkcje do konwersji danych do iz bajtów, w tym dekodowania obrazów i analizowania plików csv.
Rzadkie tensory
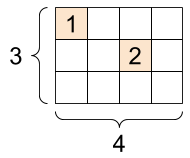
Czasami dane są rzadkie, jak bardzo szeroka przestrzeń do osadzania. TensorFlow obsługuje tf.sparse.SparseTensor i powiązane operacje w celu wydajnego przechowywania rzadkich danych.
A tf.SparseTensor , kształt: [3, 4] |
|---|
 |
# Sparse tensors store values by index in a memory-efficient manner
sparse_tensor = tf.sparse.SparseTensor(indices=[[0, 0], [1, 2]],
values=[1, 2],
dense_shape=[3, 4])
print(sparse_tensor, "\n")
# You can convert sparse tensors to dense
print(tf.sparse.to_dense(sparse_tensor))
SparseTensor(indices=tf.Tensor( [[0 0] [1 2]], shape=(2, 2), dtype=int64), values=tf.Tensor([1 2], shape=(2,), dtype=int32), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64)) tf.Tensor( [[1 0 0 0] [0 0 2 0] [0 0 0 0]], shape=(3, 4), dtype=int32)