 הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
בקולאב זה נחקור דגימה מאחור של מודל תערובת גאוס בייסיאני (BGMM) תוך שימוש רק בפרימיטיבים של TensorFlow Probability.
דֶגֶם
עבור \(k\in\{1,\ldots, K\}\) רכיבי התערובת כל מימד \(D\), אנחנו רוצים מודל \(i\in\{1,\ldots,N\}\) iid דגימות באמצעות מודל תערובת גאוס בייס הבאים:
\[\begin{align*} \theta &\sim \text{Dirichlet}(\text{concentration}=\alpha_0)\\ \mu_k &\sim \text{Normal}(\text{loc}=\mu_{0k}, \text{scale}=I_D)\\ T_k &\sim \text{Wishart}(\text{df}=5, \text{scale}=I_D)\\ Z_i &\sim \text{Categorical}(\text{probs}=\theta)\\ Y_i &\sim \text{Normal}(\text{loc}=\mu_{z_i}, \text{scale}=T_{z_i}^{-1/2})\\ \end{align*}\]
הערה, את scale הטיעונים לכולם יש cholesky סמנטיקה. אנו משתמשים במוסכמה זו מכיוון שהיא זו של TF Distributions (שבעצמה משתמשת במוסכמה זו בין השאר משום שהיא מועילה מבחינה חישובית).
המטרה שלנו היא ליצור דוגמאות מהחלק האחורי:
\[p\left(\theta, \{\mu_k, T_k\}_{k=1}^K \Big| \{y_i\}_{i=1}^N, \alpha_0, \{\mu_{ok}\}_{k=1}^K\right)\]
שימו לב כי \(\{Z_i\}_{i=1}^N\) אינו נוכח - אנו מעוניינים אלה משתנים אקראיים בלבד אשר לא בקנה מידה עם \(N\). (ולמרבה המזל יש חלוקה TF שמטפלת לשוליים את \(Z_i\).)
לא ניתן לדגום ישירות מהתפלגות זו עקב מונח נורמליזציה בלתי ניתנת לפתרון חישובי.
מטרופוליס-הייסטינגס אלגוריתמים הם טכניקה עבור דגימה מן ההפצות סוררות אלי לנרמל.
TensorFlow Probability מציעה מספר אפשרויות MCMC, כולל כמה המבוססות על Metropolis-Hastings. במחברת זו, נשתמש והמילטון מונטה קרלו ( tfp.mcmc.HamiltonianMonteCarlo ). HMC הוא לעתים קרובות בחירה טובה מכיוון שהוא יכול להתכנס במהירות, לדגום את מרחב המצב במשותף (בניגוד לקואורדינטות), וממנף את אחת המעלות של TF: בידול אוטומטי. עם זאת, דגימה מתוך אחורי BGMM באמת עשוי להיעשות טוב יותר על ידי גישות אחרות, למשל, הדגימה של גיב .
%matplotlib inline
import functools
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import seaborn as sns; sns.set_context('notebook')
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
physical_devices = tf.config.experimental.list_physical_devices('GPU')
if len(physical_devices) > 0:
tf.config.experimental.set_memory_growth(physical_devices[0], True)
לפני בניית המודל בפועל, נצטרך להגדיר סוג חדש של הפצה. ממפרט המודל שלמעלה, ברור שאנחנו מפרמטרים את ה-MVN עם מטריצת שיתוף פעולה הפוכה, כלומר, [מטריצת דיוק](https://en.wikipedia.org/wiki/Precision_(statistics%29). כדי להשיג זאת ב- TF, נצטרך לרדד שלנו Bijector זה. Bijector ישתמש טרנספורמציה קדימה:
-
Y = tf.linalg.triangular_solve((tf.linalg.matrix_transpose(chol_precision_tril), X, adjoint=True) + loc.
וגם log_prob החישוב הוא פשוט ההופכי, כלומר:
-
X = tf.linalg.matmul(chol_precision_tril, X - loc, adjoint_a=True).
מאז כל צורך שאנחנו עבור HMC היא log_prob , אמצעי זה אנו נמנעים אי פעם קורא tf.linalg.triangular_solve (כפי שהיה קורה עבור tfd.MultivariateNormalTriL ). זהו יתרון מאז tf.linalg.matmul היא בדרך כלל מהירה יותר בשל יישוב מטמון טוב יותר.
class MVNCholPrecisionTriL(tfd.TransformedDistribution):
"""MVN from loc and (Cholesky) precision matrix."""
def __init__(self, loc, chol_precision_tril, name=None):
super(MVNCholPrecisionTriL, self).__init__(
distribution=tfd.Independent(tfd.Normal(tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=chol_precision_tril,
adjoint=True)),
]),
name=name)
tfd.Independent עצמאי תורות הפצה שואבת של הפצה אחת, לתוך פונקצית התפלגות רבה עם קואורדינטות עצמאיות מבחינה סטטיסטית. במונחי מחשוב log_prob , זה "מטא-הפצה" מניפסטים כסכום פשוט פני מאפיין האירוע (הים).
שימו לב גם לקחנו את adjoint ( "לשרבב") של מטריצת המידה. הסיבה לכך היא שאם הדיוק הוא שונה משותף הפוך, כלומר, \(P=C^{-1}\) ואם \(C=AA^\top\), אז \(P=BB^{\top}\) שבו \(B=A^{-\top}\).
מאז ההפצה הזו היא סוג של מסובך, בואו לבדוק במהירות כי שלנו MVNCholPrecisionTriL עובד כמו שאנחנו חושבים שהוא צריך.
def compute_sample_stats(d, seed=42, n=int(1e6)):
x = d.sample(n, seed=seed)
sample_mean = tf.reduce_mean(x, axis=0, keepdims=True)
s = x - sample_mean
sample_cov = tf.linalg.matmul(s, s, adjoint_a=True) / tf.cast(n, s.dtype)
sample_scale = tf.linalg.cholesky(sample_cov)
sample_mean = sample_mean[0]
return [
sample_mean,
sample_cov,
sample_scale,
]
dtype = np.float32
true_loc = np.array([1., -1.], dtype=dtype)
true_chol_precision = np.array([[1., 0.],
[2., 8.]],
dtype=dtype)
true_precision = np.matmul(true_chol_precision, true_chol_precision.T)
true_cov = np.linalg.inv(true_precision)
d = MVNCholPrecisionTriL(
loc=true_loc,
chol_precision_tril=true_chol_precision)
[sample_mean, sample_cov, sample_scale] = [
t.numpy() for t in compute_sample_stats(d)]
print('true mean:', true_loc)
print('sample mean:', sample_mean)
print('true cov:\n', true_cov)
print('sample cov:\n', sample_cov)
true mean: [ 1. -1.] sample mean: [ 1.0002806 -1.000105 ] true cov: [[ 1.0625 -0.03125 ] [-0.03125 0.015625]] sample cov: [[ 1.0641273 -0.03126175] [-0.03126175 0.01559312]]
מכיוון שממוצע הדגימה והשונות קרובים לממוצע והשונות האמיתיים, נראה שההתפלגות מיושמת בצורה נכונה. עכשיו, נשתמש MVNCholPrecisionTriL tfp.distributions.JointDistributionNamed לציין את הדגם BGMM. עבור המודל תצפיתיים, נשתמש tfd.MixtureSameFamily לשלב באופן אוטומטי את \(\{Z_i\}_{i=1}^N\) שואבת.
dtype = np.float64
dims = 2
components = 3
num_samples = 1000
bgmm = tfd.JointDistributionNamed(dict(
mix_probs=tfd.Dirichlet(
concentration=np.ones(components, dtype) / 10.),
loc=tfd.Independent(
tfd.Normal(
loc=np.stack([
-np.ones(dims, dtype),
np.zeros(dims, dtype),
np.ones(dims, dtype),
]),
scale=tf.ones([components, dims], dtype)),
reinterpreted_batch_ndims=2),
precision=tfd.Independent(
tfd.WishartTriL(
df=5,
scale_tril=np.stack([np.eye(dims, dtype=dtype)]*components),
input_output_cholesky=True),
reinterpreted_batch_ndims=1),
s=lambda mix_probs, loc, precision: tfd.Sample(tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(probs=mix_probs),
components_distribution=MVNCholPrecisionTriL(
loc=loc,
chol_precision_tril=precision)),
sample_shape=num_samples)
))
def joint_log_prob(observations, mix_probs, loc, chol_precision):
"""BGMM with priors: loc=Normal, precision=Inverse-Wishart, mix=Dirichlet.
Args:
observations: `[n, d]`-shaped `Tensor` representing Bayesian Gaussian
Mixture model draws. Each sample is a length-`d` vector.
mix_probs: `[K]`-shaped `Tensor` representing random draw from
`Dirichlet` prior.
loc: `[K, d]`-shaped `Tensor` representing the location parameter of the
`K` components.
chol_precision: `[K, d, d]`-shaped `Tensor` representing `K` lower
triangular `cholesky(Precision)` matrices, each being sampled from
a Wishart distribution.
Returns:
log_prob: `Tensor` representing joint log-density over all inputs.
"""
return bgmm.log_prob(
mix_probs=mix_probs, loc=loc, precision=chol_precision, s=observations)
צור נתוני "הדרכה".
עבור הדגמה זו, נדגום כמה נתונים אקראיים.
true_loc = np.array([[-2., -2],
[0, 0],
[2, 2]], dtype)
random = np.random.RandomState(seed=43)
true_hidden_component = random.randint(0, components, num_samples)
observations = (true_loc[true_hidden_component] +
random.randn(num_samples, dims).astype(dtype))
היסק בייסיאני באמצעות HMC
כעת, לאחר שהשתמשנו ב-TFD כדי לציין את המודל שלנו והשגנו כמה נתונים שנצפו, יש לנו את כל החלקים הדרושים להפעלת HMC.
לשם כך, נשתמש יישום חלקי כדי "למנוע התחמקות" הדברים שאנחנו לא רוצים מדגם. במקרה זה זה אומר שאנחנו צריכים להצמיד רק observations . (The-פרמטרי Hyper כבר אפוי על החלוקות הקודמות ולא חלק joint_log_prob חתימת הפונקציה.)
unnormalized_posterior_log_prob = functools.partial(joint_log_prob, observations)
initial_state = [
tf.fill([components],
value=np.array(1. / components, dtype),
name='mix_probs'),
tf.constant(np.array([[-2., -2],
[0, 0],
[2, 2]], dtype),
name='loc'),
tf.linalg.eye(dims, batch_shape=[components], dtype=dtype, name='chol_precision'),
]
ייצוג ללא הגבלה
המילטון מונטה קרלו (HMC) דורש שפונקציית ההסתברות של היעד תהיה ניתנת להבדלה ביחס לארגומנטים שלה. יתר על כן, HMC יכול להפגין יעילות סטטיסטית גבוהה יותר באופן דרמטי אם מרחב המדינה אינו מוגבל.
המשמעות היא שנצטרך לפתור שתי בעיות עיקריות בעת דגימה מה-BGMM האחורי:
- \(\theta\) מייצג וקטור הסתברות דיסקרטית, כלומר, חייב להיות כזה \(\sum_{k=1}^K \theta_k = 1\) ו \(\theta_k>0\).
- \(T_k\) מייצג פוך שונה המשותפת מטריקס, כלומר, חייב להיות כזה כי \(T_k \succ 0\), כלומר, הוא חיובי מובהק .
כדי לענות על הדרישה הזו נצטרך:
- להפוך את המשתנים המוגבלים למרחב לא מוגבל
- הפעל את ה-MCMC במרחב לא מוגבל
- להפוך את המשתנים הלא מוגבלים בחזרה למרחב המוגבל.
כמו עם MVNCholPrecisionTriL , נשתמש Bijector ים להפוך משתנים אקראיים לחלל מאולצת.
Dirichletהופכת לחלל מאולץ באמצעות פונקצית softmax .המשתנה האקראי המדויק שלנו הוא התפלגות על פני מטריצות חצי מוגדרות חיוביות. כדי בטל את אילוץ אלה נשתמש
FillTriangularוTransformDiagonalbijectors. אלה ממירים וקטורים למטריצות משולשות נמוכות יותר ומבטיחים שהאלכסון חיובי. הראשון הוא שימושי משום שהוא מאפשר לדגום רק \(d(d+1)/2\) צף ולא \(d^2\).
unconstraining_bijectors = [
tfb.SoftmaxCentered(),
tfb.Identity(),
tfb.Chain([
tfb.TransformDiagonal(tfb.Softplus()),
tfb.FillTriangular(),
])]
@tf.function(autograph=False)
def sample():
return tfp.mcmc.sample_chain(
num_results=2000,
num_burnin_steps=500,
current_state=initial_state,
kernel=tfp.mcmc.SimpleStepSizeAdaptation(
tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
step_size=0.065,
num_leapfrog_steps=5),
bijector=unconstraining_bijectors),
num_adaptation_steps=400),
trace_fn=lambda _, pkr: pkr.inner_results.inner_results.is_accepted)
[mix_probs, loc, chol_precision], is_accepted = sample()
כעת נבצע את השרשרת ונדפיס את האמצעים האחוריים.
acceptance_rate = tf.reduce_mean(tf.cast(is_accepted, dtype=tf.float32)).numpy()
mean_mix_probs = tf.reduce_mean(mix_probs, axis=0).numpy()
mean_loc = tf.reduce_mean(loc, axis=0).numpy()
mean_chol_precision = tf.reduce_mean(chol_precision, axis=0).numpy()
precision = tf.linalg.matmul(chol_precision, chol_precision, transpose_b=True)
print('acceptance_rate:', acceptance_rate)
print('avg mix probs:', mean_mix_probs)
print('avg loc:\n', mean_loc)
print('avg chol(precision):\n', mean_chol_precision)
acceptance_rate: 0.5305 avg mix probs: [0.25248723 0.60729516 0.1402176 ] avg loc: [[-1.96466753 -2.12047249] [ 0.27628865 0.22944732] [ 2.06461244 2.54216122]] avg chol(precision): [[[ 1.05105032 0. ] [ 0.12699955 1.06553113]] [[ 0.76058015 0. ] [-0.50332767 0.77947431]] [[ 1.22770457 0. ] [ 0.70670027 1.50914164]]]
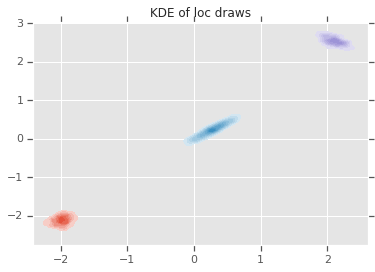
loc_ = loc.numpy()
ax = sns.kdeplot(loc_[:,0,0], loc_[:,0,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,1,0], loc_[:,1,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,2,0], loc_[:,2,1], shade=True, shade_lowest=False)
plt.title('KDE of loc draws');
סיכום
קולב פשוט זה הדגים כיצד ניתן להשתמש בפרימיטיבים של TensorFlow Probability לבניית מודלים היררכיים של תערובת בייסיאנית.
