عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
هذا reimplements المحمولة ويمتد "تحليل نقطة التغيير" النظرية الافتراضية المثال من الوثائق pymc3 .
المتطلبات الأساسية
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,8)
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
مجموعة البيانات
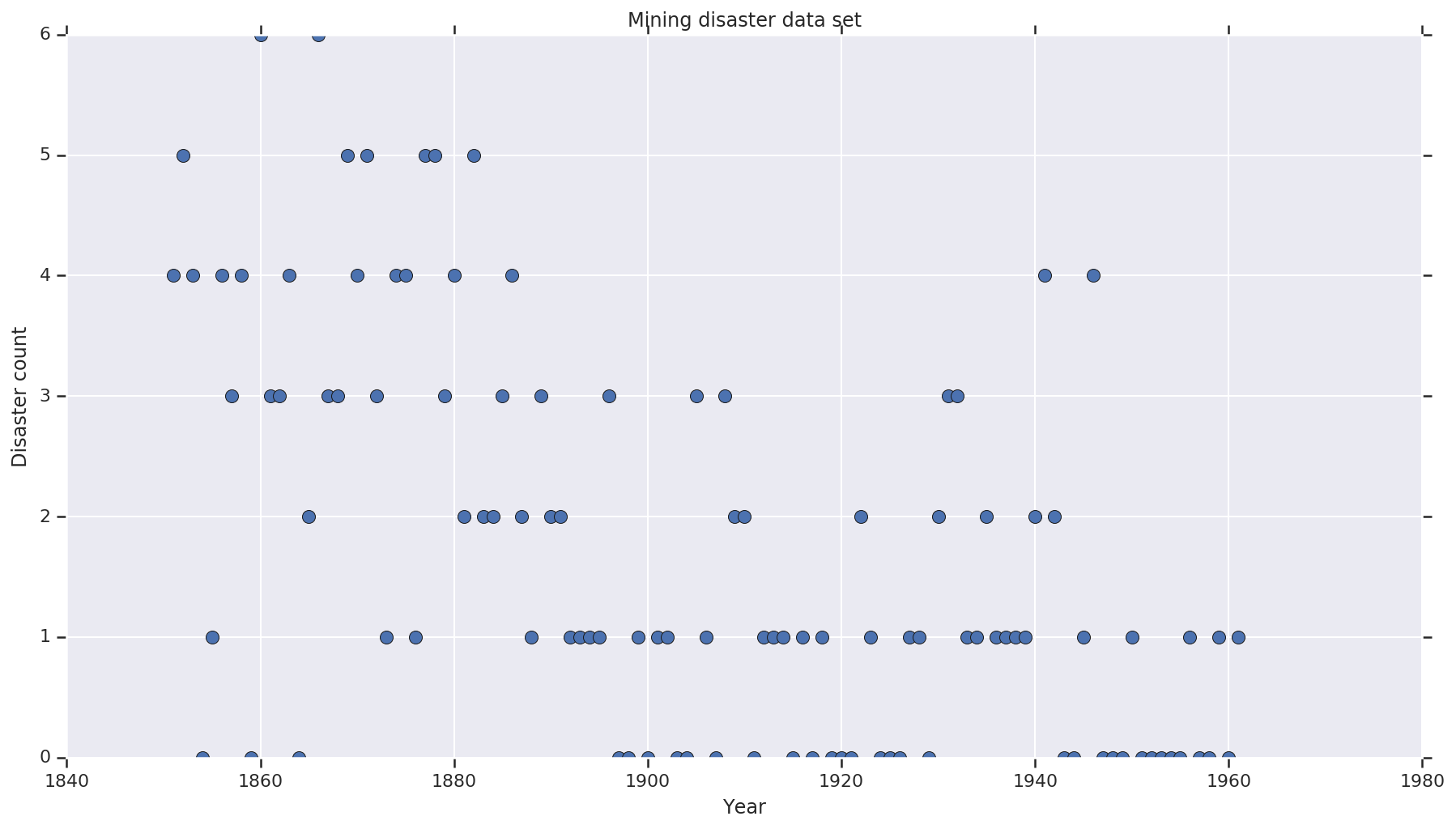
مجموعة البيانات هو من هنا . ملاحظة، هناك نسخة أخرى من هذا المثال وتطوف ، لكنها "مفقود" البيانات - في هذه الحالة كنت بحاجة إلى عزو القيم المفقودة. (وإلا فلن يترك نموذجك المعلمات الأولية أبدًا لأن دالة الاحتمال ستكون غير محددة.)
disaster_data = np.array([ 4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
2, 2, 3, 4, 2, 1, 3, 2, 2, 1, 1, 1, 1, 3, 0, 0,
1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
3, 3, 1, 1, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1])
years = np.arange(1851, 1962)
plt.plot(years, disaster_data, 'o', markersize=8);
plt.ylabel('Disaster count')
plt.xlabel('Year')
plt.title('Mining disaster data set')
plt.show()
النموذج الاحتمالي
يفترض النموذج "نقطة تبديل" (على سبيل المثال ، السنة التي تغيرت خلالها لوائح السلامة) ، ومعدل الكوارث الموزع بواسون بمعدلات ثابتة (ولكن من المحتمل أن تكون مختلفة) قبل نقطة التبديل هذه وبعدها.
عدد الكوارث الفعلي ثابت (ملاحظ) ؛ أي عينة من هذا النموذج سوف تحتاج إلى تحديد كل من نقطة التبديل والمعدل "المبكر" و "المتأخر" للكوارث.
النموذج الأصلي من سبيل المثال وثائق pymc3 :
\[ \begin{align*} (D_t|s,e,l)&\sim \text{Poisson}(r_t), \\ & \,\quad\text{with}\; r_t = \begin{cases}e & \text{if}\; t < s\\l &\text{if}\; t \ge s\end{cases} \\ s&\sim\text{Discrete Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
ومع ذلك، فإن متوسط معدل كارثة \(r_t\) لديه انقطاع في switchpoint \(s\)، مما يجعله لا تفاضل. وبالتالي فإنه لا يقدم أي إشارة التدرج إلى (HMC) خوارزمية هاملتون مونت كارلو - ولكن لأن \(s\) هو قبل المستمر، تراجع مؤسسة حمد الطبية إلى المشي العشوائي غير كافية جيدة للعثور على مناطق كتلة عالية الاحتمال في هذا المثال.
كنموذج الثاني، فإننا تعديل النموذج الأصلي باستخدام السيني "التبديل" بين البريد ولام لجعل الانتقال للتفاضل، واستخدام توزيع الزي المستمر لswitchpoint \(s\). (يمكن للمرء أن يجادل بأن هذا النموذج أكثر صدقًا مع الواقع ، حيث من المحتمل أن يمتد "التبديل" في متوسط المعدل على مدى عدة سنوات.) النموذج الجديد هو:
\[ \begin{align*} (D_t|s,e,l)&\sim\text{Poisson}(r_t), \\ & \,\quad \text{with}\; r_t = e + \frac{1}{1+\exp(s-t)}(l-e) \\ s&\sim\text{Uniform}(t_l,\,t_h) \\ e&\sim\text{Exponential}(r_e)\\ l&\sim\text{Exponential}(r_l) \end{align*} \]
في غياب مزيد من المعلومات افترضنا \(r_e = r_l = 1\) كمعلمات للمقدمو الاديره. سنقوم بتشغيل كلا النموذجين ومقارنة نتائج الاستدلال.
def disaster_count_model(disaster_rate_fn):
disaster_count = tfd.JointDistributionNamed(dict(
e=tfd.Exponential(rate=1.),
l=tfd.Exponential(rate=1.),
s=tfd.Uniform(0., high=len(years)),
d_t=lambda s, l, e: tfd.Independent(
tfd.Poisson(rate=disaster_rate_fn(np.arange(len(years)), s, l, e)),
reinterpreted_batch_ndims=1)
))
return disaster_count
def disaster_rate_switch(ys, s, l, e):
return tf.where(ys < s, e, l)
def disaster_rate_sigmoid(ys, s, l, e):
return e + tf.sigmoid(ys - s) * (l - e)
model_switch = disaster_count_model(disaster_rate_switch)
model_sigmoid = disaster_count_model(disaster_rate_sigmoid)
يحدد الكود أعلاه النموذج عبر التوزيعات المتسلسلة المشتركة. و disaster_rate تسمى الوظائف مع مجموعة من [0, ..., len(years)-1] لإنتاج متجه len(years) المتغيرات العشوائية - السنوات التي سبقت switchpoint هي early_disaster_rate ، هم بعد late_disaster_rate (MODULO لل الانتقال السيني).
فيما يلي تحقق من صحة أن وظيفة احتمال السجل الهدف عاقلة:
def target_log_prob_fn(model, s, e, l):
return model.log_prob(s=s, e=e, l=l, d_t=disaster_data)
models = [model_switch, model_sigmoid]
print([target_log_prob_fn(m, 40., 3., .9).numpy() for m in models]) # Somewhat likely result
print([target_log_prob_fn(m, 60., 1., 5.).numpy() for m in models]) # Rather unlikely result
print([target_log_prob_fn(m, -10., 1., 1.).numpy() for m in models]) # Impossible result
[-176.94559, -176.28717] [-371.3125, -366.8816] [-inf, -inf]
مؤسسة حمد الطبية للقيام بالاستدلال بايزي
نحدد عدد النتائج وخطوات الإنجاز المطلوبة ؛ رمز على غرار معظمها بعد توثيق tfp.mcmc.HamiltonianMonteCarlo . يستخدم حجم خطوة تكيفي (وإلا تكون النتيجة حساسة للغاية لقيمة حجم الخطوة المختارة). نستخدم قيم واحد كحالة أولية للسلسلة.
هذه ليست القصة الكاملة بالرغم من ذلك. إذا عدت إلى تعريف النموذج أعلاه ، فستلاحظ أن بعض التوزيعات الاحتمالية غير محددة جيدًا على خط الأعداد الحقيقي بالكامل. ولذلك نحن تقييد المساحة التي مؤسسة حمد الطبية بفحص التفاف نواة مؤسسة حمد الطبية مع TransformedTransitionKernel يحدد bijectors إلى الأمام لتحويل الأرقام الحقيقية على المجال الذي يتم تعريف التوزيع الاحتمالي على (انظر تعليقات في التعليمات البرمجية أدناه).
num_results = 10000
num_burnin_steps = 3000
@tf.function(autograph=False, jit_compile=True)
def make_chain(target_log_prob_fn):
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.05,
num_leapfrog_steps=3),
bijector=[
# The switchpoint is constrained between zero and len(years).
# Hence we supply a bijector that maps the real numbers (in a
# differentiable way) to the interval (0;len(yers))
tfb.Sigmoid(low=0., high=tf.cast(len(years), dtype=tf.float32)),
# Early and late disaster rate: The exponential distribution is
# defined on the positive real numbers
tfb.Softplus(),
tfb.Softplus(),
])
kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=int(0.8*num_burnin_steps))
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
# The three latent variables
tf.ones([], name='init_switchpoint'),
tf.ones([], name='init_early_disaster_rate'),
tf.ones([], name='init_late_disaster_rate'),
],
trace_fn=None,
kernel=kernel)
return states
switch_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_switch, *args))]
sigmoid_samples = [s.numpy() for s in make_chain(
lambda *args: target_log_prob_fn(model_sigmoid, *args))]
switchpoint, early_disaster_rate, late_disaster_rate = zip(
switch_samples, sigmoid_samples)
قم بتشغيل كلا الطرازين بالتوازي:
تصور النتيجة
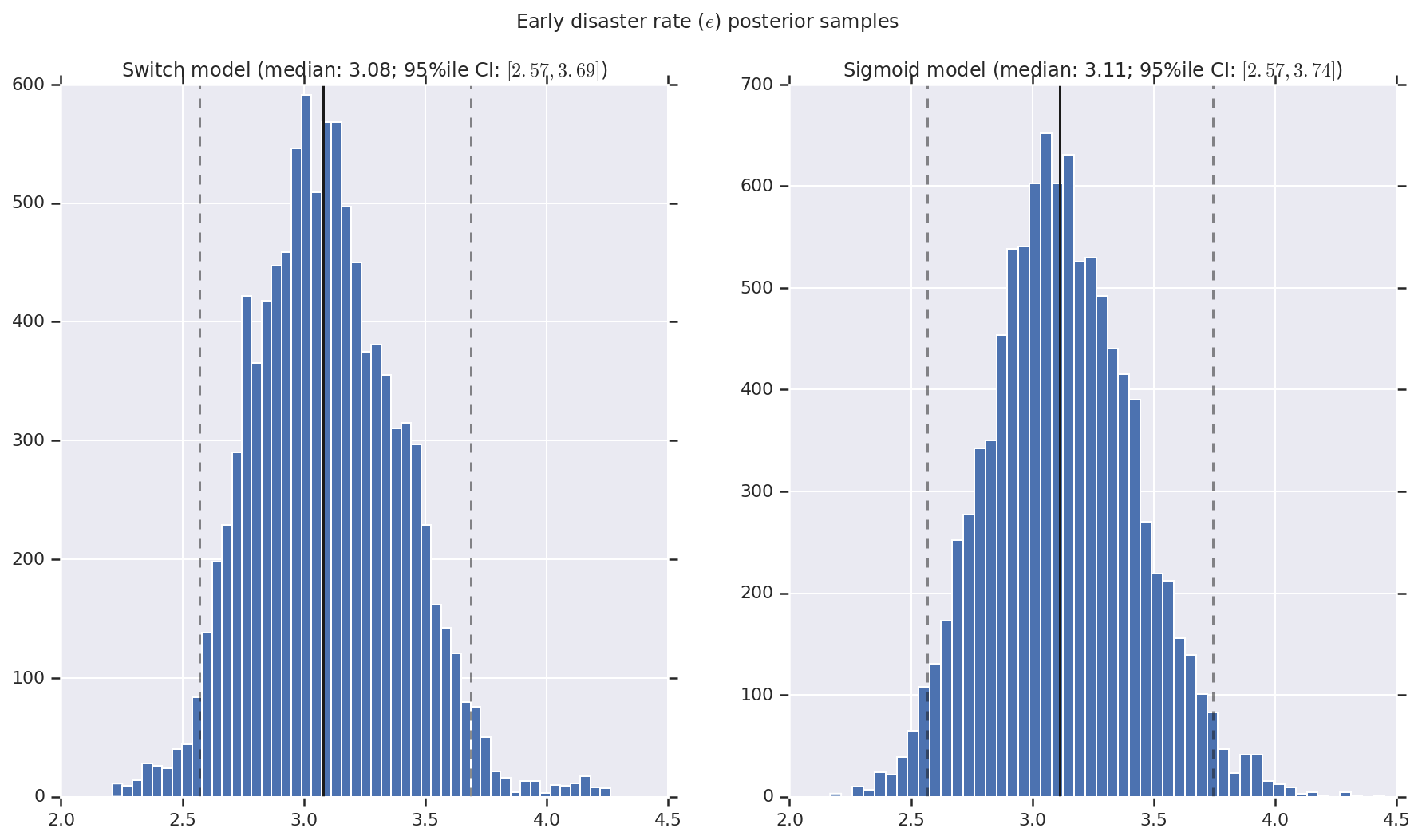
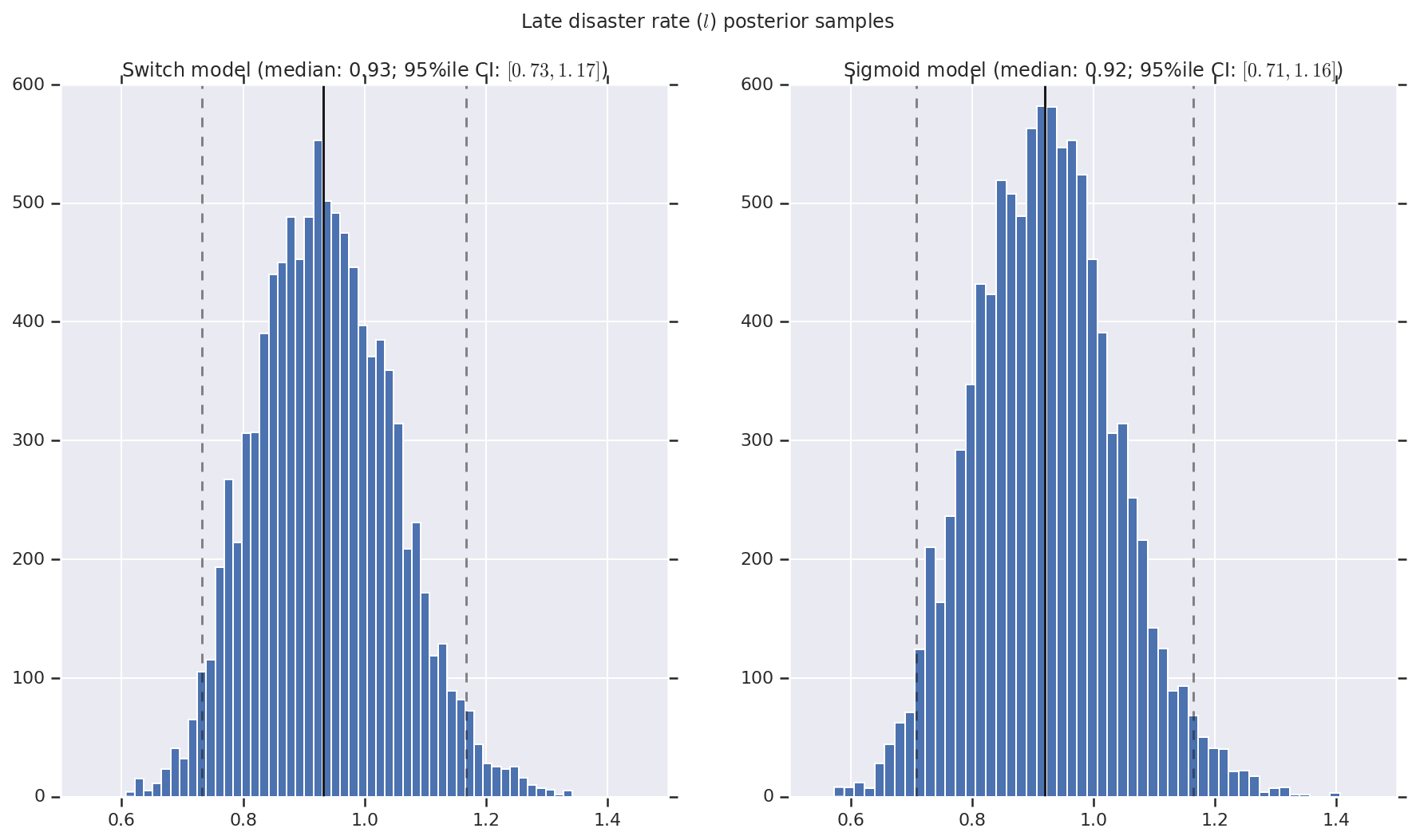
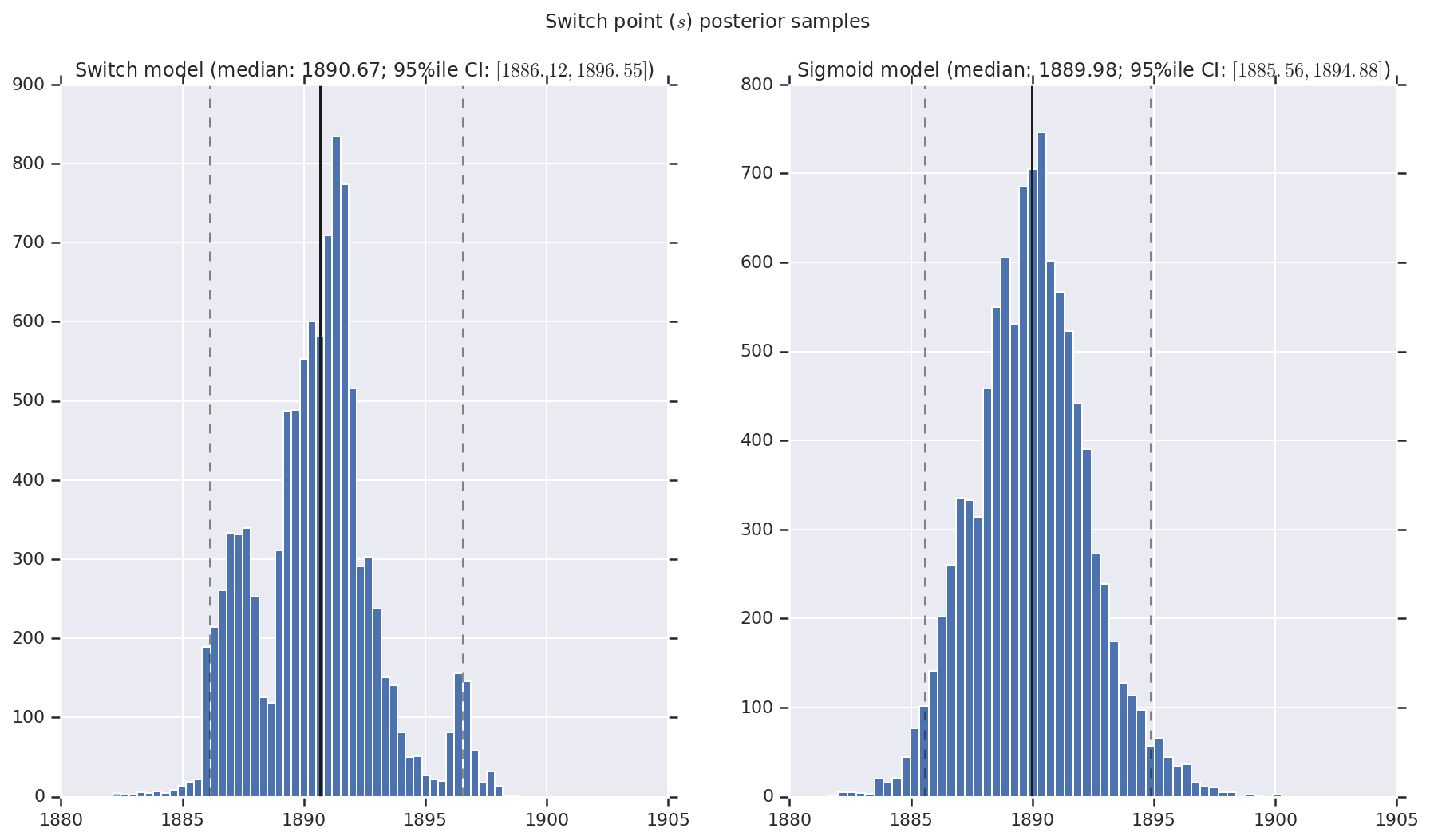
نحن نتخيل النتيجة على شكل رسوم بيانية لعينات من التوزيع اللاحق لمعدل الكارثة المبكرة والمتأخرة ، بالإضافة إلى نقطة التبديل. يتم تراكب الرسوم البيانية بخط متصل يمثل متوسط العينة ، بالإضافة إلى حدود الفاصل الزمني الموثوقة 95٪ كخطوط متقطعة.
def _desc(v):
return '(median: {}; 95%ile CI: $[{}, {}]$)'.format(
*np.round(np.percentile(v, [50, 2.5, 97.5]), 2))
for t, v in [
('Early disaster rate ($e$) posterior samples', early_disaster_rate),
('Late disaster rate ($l$) posterior samples', late_disaster_rate),
('Switch point ($s$) posterior samples', years[0] + switchpoint),
]:
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True)
for (m, i) in (('Switch', 0), ('Sigmoid', 1)):
a = ax[i]
a.hist(v[i], bins=50)
a.axvline(x=np.percentile(v[i], 50), color='k')
a.axvline(x=np.percentile(v[i], 2.5), color='k', ls='dashed', alpha=.5)
a.axvline(x=np.percentile(v[i], 97.5), color='k', ls='dashed', alpha=.5)
a.set_title(m + ' model ' + _desc(v[i]))
fig.suptitle(t)
plt.show()