COVID-19'un Avrupa'da yayılmasının modellenmesi ve müdahalelerin etkisi

MIT Lisansı altında lisanslıdır

TensorFlow.org'da görüntüleyin Google Colab'da çalıştırın Kaynağı GitHub'da görüntüleyin Not defterini indir

2020'nin başlarında COVID-19'un yayılmasını yavaşlatmak için Avrupa ülkeleri, zorunlu olmayan işletmelerin kapatılması, bireysel vakaların izolasyonu, seyahat yasakları ve sosyal mesafeyi teşvik etmek için diğer önlemler gibi ilaç dışı müdahaleleri benimsedi. Imperial College COVID-19 Tepki Ekibi onların yazıda bu önlemlerin etkinliğini analiz "enfeksiyonlarının süresini ve 11 Avrupa ülkesinde COVID-19 farmasötik olmayan müdahalelerin etkisini tahmin" mekanistik ile birlikte Bayes hiyerarşik modeli kullanılarak, epidemiyolojik model.

Bu İşbirliği, bu analizin aşağıdaki şekilde organize edilmiş bir TensorFlow Olasılığı (TFP) uygulamasını içerir:

  • "Model kurulumu", hastalık bulaşması ve sonuçta ortaya çıkan ölümler için epidemiyolojik modeli, model parametreleri üzerindeki Bayesian önceki dağılımını ve parametre değerlerine bağlı ölüm sayısının dağılımını tanımlar.
  • "Veri ön işleme", her ülkedeki müdahalelerin zamanlaması ve türü, zaman içindeki ölüm sayıları ve enfekte olanlar için tahmini ölüm oranları hakkındaki verileri yükler.
  • "Model çıkarımı", Bayes hiyerarşik bir model oluşturur ve parametreler üzerindeki sonsal dağılımdan örnek almak için Hamiltonian Monte Carlo'yu (HMC) çalıştırır.
  • "Sonuçlar", müdahalelerin yokluğunda öngörülen ölümler ve karşı olgusal ölümler gibi ilgili miktarlar için sonradan tahmin dağılımlarını gösterir.

Kağıt ülkeler her enfekte kişi (tarafından iletilen yeni enfeksiyonların sayısını azaltmak başarmıştı dair kanıt bulduklarını\(R_t\)), ama bu güvenilir aralıklar bulunan \(R_t=1\) (salgınının devam ettiği yukarıdaki değerini) ve prematüre olduğunu müdahalelerin etkinliği hakkında güçlü sonuçlar çıkarmak. Kağıt için Stan kod yazarların olduğu Github depo ve bu CoLab yeniden üretir Sürüm 2 .

pip3 install -q git+git://github.com/arviz-devs/arviz.git
pip3 install -q tf-nightly tfp-nightly

ithalat

1 Model kurulumu

1.1 Enfeksiyonlar ve ölümler için mekanik model

Enfeksiyon modeli, zaman içinde her ülkedeki enfeksiyon sayısını simüle eder. Girdi verileri, müdahalelerin zamanlaması ve türü, popülasyon büyüklüğü ve ilk vakalardır. Parametreler, müdahalelerin etkinliğini ve hastalık bulaşma oranını kontrol eder. Beklenen ölüm sayısı modeli, tahmin edilen enfeksiyonlara bir ölüm oranı uygular.

Bulaşma modeli, seri aralık dağılımıyla (enfekte olma ve başka birine bulaşma arasındaki gün sayısı üzerinden dağılım) önceki günlük bulaşmaların bir evrişini gerçekleştirir. Her adımda, zaman yeni enfeksiyonların sayısının \(t\), \(n_t\), şu şekilde hesaplanır

\begin{denklem} \sum_{i=0}^{t-1} n_i \mu_t \text{p} (\text{} i | \text{} t'de yeni enfekte olmuş birinden yakalandı) \end{ denklem} burada \(\mu_t=R_t\) ve şartlı olasılık saklanır conv_serial_interval , aşağıda tanımlandığı gibidir.

Beklenen ölümler için model, günlük enfeksiyonların bir kıvrımını ve enfeksiyon ile ölüm arasındaki günlerin dağılımını gerçekleştirir. Yani, günde beklenen ölümler olduğu \(t\) olarak hesaplanır

başlamak \ {denklem} \ sum_ {ı = 0} ^ {t-1} n_i \ metni {s (günde ölüm \(t\)| günde enfeksiyon \(i\))} koşullu olasılığı depolanır \ ucu {denklem} içerisinde conv_fatality_rate , aşağıda tanımlandığı gibidir.

from tensorflow_probability.python.internal import broadcast_util as bu

def predict_infections(
    intervention_indicators, population, initial_cases, mu, alpha_hier,
    conv_serial_interval, initial_days, total_days):
  """Predict the number of infections by forward-simulation.

  Args:
    intervention_indicators: Binary array of shape
      `[num_countries, total_days, num_interventions]`, in which `1` indicates
      the intervention is active in that country at that time and `0` indicates
      otherwise.
    population: Vector of length `num_countries`. Population of each country.
    initial_cases: Array of shape `[batch_size, num_countries]`. Number of cases
      in each country at the start of the simulation.
    mu: Array of shape `[batch_size, num_countries]`. Initial reproduction rate
      (R_0) by country.
    alpha_hier: Array of shape `[batch_size, num_interventions]` representing
      the effectiveness of interventions.
    conv_serial_interval: Array of shape
      `[total_days - initial_days, total_days]` output from
      `make_conv_serial_interval`. Convolution kernel for serial interval
      distribution.
    initial_days: Integer, number of sequential days to seed infections after
      the 10th death in a country. (N0 in the authors' Stan code.)
    total_days: Integer, number of days of observed data plus days to forecast.
      (N2 in the authors' Stan code.)
  Returns:
    predicted_infections: Array of shape
      `[total_days, batch_size, num_countries]`. (Batched) predicted number of
      infections over time and by country.
  """
  alpha = alpha_hier - tf.cast(np.log(1.05) / 6.0, DTYPE)

  # Multiply the effectiveness of each intervention in each country (alpha)
  # by the indicator variable for whether the intervention was active and sum
  # over interventions, yielding an array of shape
  # [total_days, batch_size, num_countries] that represents the total effectiveness of
  # all interventions in each country on each day (for a batch of data).
  linear_prediction = tf.einsum(
      'ijk,...k->j...i', intervention_indicators, alpha)

  # Adjust the reproduction rate per country downward, according to the
  # effectiveness of the interventions.
  rt = mu * tf.exp(-linear_prediction, name='reproduction_rate')

  # Initialize storage array for daily infections and seed it with initial
  # cases.
  daily_infections = tf.TensorArray(
      dtype=DTYPE, size=total_days, element_shape=initial_cases.shape)
  for i in range(initial_days):
    daily_infections = daily_infections.write(i, initial_cases)

  # Initialize cumulative cases.
  init_cumulative_infections = initial_cases * initial_days

  # Simulate forward for total_days days.
  cond = lambda i, *_: i < total_days
  def body(i, prev_daily_infections, prev_cumulative_infections):
    # The probability distribution over days j that someone infected on day i
    # caught the virus from someone infected on day j.
    p_infected_on_day = tf.gather(
        conv_serial_interval, i - initial_days, axis=0)

    # Multiply p_infected_on_day by the number previous infections each day and
    # by mu, and sum to obtain new infections on day i. Mu is adjusted by
    # the fraction of the population already infected, so that the population
    # size is the upper limit on the number of infections.
    prev_daily_infections_array = prev_daily_infections.stack()
    to_sum = prev_daily_infections_array * bu.left_justified_expand_dims_like(
        p_infected_on_day, prev_daily_infections_array)
    convolution = tf.reduce_sum(to_sum, axis=0)
    rt_adj = (
        (population - prev_cumulative_infections) / population
        ) * tf.gather(rt, i)
    new_infections = rt_adj * convolution

    # Update the prediction array and the cumulative number of infections.
    daily_infections = prev_daily_infections.write(i, new_infections)
    cumulative_infections = prev_cumulative_infections + new_infections
    return i + 1, daily_infections, cumulative_infections

  _, daily_infections_final, last_cumm_sum = tf.while_loop(
      cond, body,
      (initial_days, daily_infections, init_cumulative_infections),
      maximum_iterations=(total_days - initial_days))
  return daily_infections_final.stack()

def predict_deaths(predicted_infections, ifr_noise, conv_fatality_rate):
  """Expected number of reported deaths by country, by day.

  Args:
    predicted_infections: Array of shape
      `[total_days, batch_size, num_countries]` output from
      `predict_infections`.
    ifr_noise: Array of shape `[batch_size, num_countries]`. Noise in Infection
      Fatality Rate (IFR).
    conv_fatality_rate: Array of shape
      `[total_days - 1, total_days, num_countries]`. Convolutional kernel for
      calculating fatalities, output from `make_conv_fatality_rate`.
  Returns:
    predicted_deaths: Array of shape `[total_days, batch_size, num_countries]`.
      (Batched) predicted number of deaths over time and by country.
  """
  # Multiply the number of infections on day j by the probability of death
  # on day i given infection on day j, and sum over j. This yields the expected
  result_remainder = tf.einsum(
      'i...j,kij->k...j', predicted_infections, conv_fatality_rate) * ifr_noise

  # Concatenate the result with a vector of zeros so that the first day is
  # included.
  result_temp = 1e-15 * predicted_infections[:1]
  return tf.concat([result_temp, result_remainder], axis=0)

1.2 Parametre değerlerinden önce

Burada, model parametreleri üzerinden ortak önsel dağılımı tanımlarız. Parametre değerlerinin birçoğunun bağımsız olduğu varsayılır, böylece önceki şu şekilde ifade edilebilir:

\(\text p(\tau, y, \psi, \kappa, \mu, \alpha) = \text p(\tau)\text p(y|\tau)\text p(\psi)\text p(\kappa)\text p(\mu|\kappa)\text p(\alpha)\text p(\epsilon)\)

hangi:

  • \(\tau\) ülke başına başlangıç vaka sayısı üzerinden Üstel dağılımının ortak oranı parametresi olan \(y = y_1, ... y_{\text{num_countries} }\).
  • \(\psi\) ölümlerin sayısı için Negatif Binom dağılımında bir parametredir.
  • \(\kappa\) her ülke, ilk çoğaltma numarası üzerinden HalfNormal dağılımının ortak ölçü parametredir, \(\mu = \mu_1, ..., \mu_{\text{num_countries} }\) (her enfekte olmuş bir kişi tarafından iletilen ilave vaka sayısı gösteren).
  • \(\alpha = \alpha_1, ..., \alpha_6\) altı her bir müdahalenin etkinliğidir.
  • \(\epsilon\) (denilen ifr_noise yazarların Stan kodundan sonra, kod) Enfeksiyon Fatality Oranı (IFR) göre gürültüdür.

Bu modeli, olasılıksal grafik modellerin ifade edilmesini sağlayan bir TFP dağıtımı türü olan TFP JointDistribution olarak ifade ediyoruz.

def make_jd_prior(num_countries, num_interventions):
  return tfd.JointDistributionSequentialAutoBatched([
      # Rate parameter for the distribution of initial cases (tau).
      tfd.Exponential(rate=tf.cast(0.03, DTYPE)),

      # Initial cases for each country.
      lambda tau: tfd.Sample(
          tfd.Exponential(rate=tf.cast(1, DTYPE) / tau),
          sample_shape=num_countries),

      # Parameter in Negative Binomial model for deaths (psi).
      tfd.HalfNormal(scale=tf.cast(5, DTYPE)),

      # Parameter in the distribution over the initial reproduction number, R_0
      # (kappa).
      tfd.HalfNormal(scale=tf.cast(0.5, DTYPE)),

      # Initial reproduction number, R_0, for each country (mu).
      lambda kappa: tfd.Sample(
          tfd.TruncatedNormal(loc=3.28, scale=kappa, low=1e-5, high=1e5),
          sample_shape=num_countries),

      # Impact of interventions (alpha; shared for all countries).
      tfd.Sample(
          tfd.Gamma(tf.cast(0.1667, DTYPE), 1), sample_shape=num_interventions),

      # Multiplicative noise in Infection Fatality Rate.
      tfd.Sample(
          tfd.TruncatedNormal(
              loc=tf.cast(1., DTYPE), scale=0.1, low=1e-5, high=1e5),
              sample_shape=num_countries)
  ])

1.3 Parametre değerlerine bağlı olarak gözlenen ölümlerin olasılığı

Olabilirlik modeli anlatırken kullanılır \(p(\text{deaths} | \tau, y, \psi, \kappa, \mu, \alpha, \epsilon)\). Parametrelere bağlı olarak enfeksiyon sayısı ve beklenen ölümler için modelleri uygular ve gerçek ölümlerin bir Negatif Binom dağılımını izlediğini varsayar.

def make_likelihood_fn(
    intervention_indicators, population, deaths,
    infection_fatality_rate, initial_days, total_days):

  # Create a mask for the initial days of simulated data, as they are not
  # counted in the likelihood.
  observed_deaths = tf.constant(deaths.T[np.newaxis, ...], dtype=DTYPE)
  mask_temp = deaths != -1
  mask_temp[:, :START_DAYS] = False
  observed_deaths_mask = tf.constant(mask_temp.T[np.newaxis, ...])

  conv_serial_interval = make_conv_serial_interval(initial_days, total_days)
  conv_fatality_rate = make_conv_fatality_rate(
      infection_fatality_rate, total_days)

  def likelihood_fn(tau, initial_cases, psi, kappa, mu, alpha_hier, ifr_noise):
    # Run models for infections and expected deaths
    predicted_infections = predict_infections(
        intervention_indicators, population, initial_cases, mu, alpha_hier,
        conv_serial_interval, initial_days, total_days)
    e_deaths_all_countries = predict_deaths(
        predicted_infections, ifr_noise, conv_fatality_rate)

    # Construct the Negative Binomial distribution for deaths by country.
    mu_m = tf.transpose(e_deaths_all_countries, [1, 0, 2])
    psi_m = psi[..., tf.newaxis, tf.newaxis]
    probs = tf.clip_by_value(mu_m / (mu_m + psi_m), 1e-9, 1.)
    likelihood_elementwise = tfd.NegativeBinomial(
        total_count=psi_m, probs=probs).log_prob(observed_deaths)
    return tf.reduce_sum(
        tf.where(observed_deaths_mask,
                likelihood_elementwise,
                tf.zeros_like(likelihood_elementwise)),
        axis=[-2, -1])

  return likelihood_fn

1.4 Enfeksiyona bağlı ölüm olasılığı

Bu bölüm, enfeksiyondan sonraki günlerde ölümlerin dağılımını hesaplar. Enfeksiyondan ölüme kadar geçen sürenin, enfeksiyondan hastalığın başlangıcına kadar geçen süreyi ve başlangıçtan ölüme kadar geçen süreyi temsil eden iki Gama değişkeni miktarının toplamı olduğunu varsayar. Zaman-ölüm dağıtım Enfeksiyon bir ölüm oranı verilerle birleştirilir Verity ve diğ. (2020) enfeksiyonu izleyen günlerde ölüm olasılığını hesaplamak için.

def daily_fatality_probability(infection_fatality_rate, total_days):
  """Computes the probability of death `d` days after infection."""

  # Convert from alternative Gamma parametrization and construct distributions
  # for number of days from infection to onset and onset to death.
  concentration1 = tf.cast((1. / 0.86)**2, DTYPE)
  rate1 = concentration1 / 5.1
  concentration2 = tf.cast((1. / 0.45)**2, DTYPE)
  rate2 = concentration2 / 18.8
  infection_to_onset = tfd.Gamma(concentration=concentration1, rate=rate1)
  onset_to_death = tfd.Gamma(concentration=concentration2, rate=rate2)

  # Create empirical distribution for number of days from infection to death.
  inf_to_death_dist = tfd.Empirical(
      infection_to_onset.sample([5e6]) + onset_to_death.sample([5e6]))

  # Subtract the CDF value at day i from the value at day i + 1 to compute the
  # probability of death on day i given infection on day 0, and given that
  # death (not recovery) is the outcome.
  times = np.arange(total_days + 1., dtype=DTYPE) + 0.5
  cdf = inf_to_death_dist.cdf(times).numpy()
  f_before_ifr = cdf[1:] - cdf[:-1]
  # Explicitly set the zeroth value to the empirical cdf at time 1.5, to include
  # the mass between time 0 and time .5.
  f_before_ifr[0] = cdf[1]

  # Multiply the daily fatality rates conditional on infection and eventual
  # death (f_before_ifr) by the infection fatality rates (probability of death
  # given intection) to obtain the probability of death on day i conditional
  # on infection on day 0.
  return infection_fatality_rate[..., np.newaxis] * f_before_ifr

def make_conv_fatality_rate(infection_fatality_rate, total_days):
  """Computes the probability of death on day `i` given infection on day `j`."""
  p_fatal_all_countries = daily_fatality_probability(
      infection_fatality_rate, total_days)

  # Use the probability of death d days after infection in each country
  # to build an array of shape [total_days - 1, total_days, num_countries],
  # where the element [i, j, c] is the probability of death on day i+1 given
  # infection on day j in country c.
  conv_fatality_rate = np.zeros(
      [total_days - 1, total_days, p_fatal_all_countries.shape[0]])
  for n in range(1, total_days):
    conv_fatality_rate[n - 1, 0:n, :] = (
        p_fatal_all_countries[:, n - 1::-1]).T
  return tf.constant(conv_fatality_rate, dtype=DTYPE)

1.5 Seri Aralığı

Seri aralık, bir hastalık bulaşma zincirindeki ardışık vakalar arasındaki zamandır ve Gamma dağılımı olduğu varsayılır. Biz günde enfekte bir kişinin olasılığını hesaplamak için seri aralık dağılımının kullanılıp \(i\) önce günde enfekte bir kişinin virüs yakalandı \(j\) ( conv_serial_interval için argüman predict_infections ).

def make_conv_serial_interval(initial_days, total_days):
  """Construct the convolutional kernel for infection timing."""

  g = tfd.Gamma(tf.cast(1. / (0.62**2), DTYPE), 1./(6.5*0.62**2))
  g_cdf = g.cdf(np.arange(total_days, dtype=DTYPE))

  # Approximate the probability mass function for the number of days between
  # successive infections.
  serial_interval = g_cdf[1:] - g_cdf[:-1]

  # `conv_serial_interval` is an array of shape
  # [total_days - initial_days, total_days] in which entry [i, j] contains the
  # probability that an individual infected on day i + initial_days caught the
  # virus from someone infected on day j.
  conv_serial_interval = np.zeros([total_days - initial_days, total_days])
  for n in range(initial_days, total_days):
    conv_serial_interval[n - initial_days, 0:n] = serial_interval[n - 1::-1]
  return tf.constant(conv_serial_interval, dtype=DTYPE)

2 Veri Ön İşleme

COUNTRIES = [
    'Austria',
    'Belgium',
    'Denmark',
    'France',
    'Germany',
    'Italy',
    'Norway',
    'Spain',
    'Sweden',
    'Switzerland',
    'United_Kingdom'
]

2.1 Müdahale verilerini alma ve ön işleme

2.2 Vaka/ölüm verilerini alın ve müdahalelere katılın

2.3 Enfekte Ölüm Oranı ve nüfus verilerini alın ve işleyin

2.4 Ülkeye özgü verileri ön işleme

# Model up to 75 days of data for each country, starting 30 days before the
# tenth cumulative death.
START_DAYS = 30
MAX_DAYS = 102
COVARIATE_COLUMNS = any_intervention_list + ['any_intervention']

# Initialize an array for number of deaths.
deaths = -np.ones((num_countries, MAX_DAYS), dtype=DTYPE)

# Assuming every intervention is still inplace in the unobserved future
num_interventions = len(COVARIATE_COLUMNS)
intervention_indicators = np.ones((num_countries, MAX_DAYS, num_interventions))

first_days = {}
for i, c in enumerate(COUNTRIES):
  c_data = data.loc[c]

  # Include data only after 10th death in a country.
  mask = c_data['deaths'].cumsum() >= 10

  # Get the date that the epidemic starts in a country.
  first_day = c_data.index[mask][0] - pd.to_timedelta(START_DAYS, 'days')
  c_data = c_data.truncate(before=first_day)

  # Truncate the data after 28 March 2020 for comparison with Flaxman et al.
  c_data = c_data.truncate(after='2020-03-28')

  c_data = c_data.iloc[:MAX_DAYS]
  days_of_data = c_data.shape[0]
  deaths[i, :days_of_data] = c_data['deaths']
  intervention_indicators[i, :days_of_data] = c_data[
    COVARIATE_COLUMNS].to_numpy()
  first_days[c] = first_day

# Number of sequential days to seed infections after the 10th death in a
# country. (N0 in authors' Stan code.)
INITIAL_DAYS = 6

# Number of days of observed data plus days to forecast. (N2 in authors' Stan
# code.)
TOTAL_DAYS = deaths.shape[1]

3 Model çıkarımı

Flaxman ve ark. (2020 yılında) kullanılan Stan'i Hamilton Monte Carlo (HMC) ve No-U dönüş Sampler (BBS) ile parametre posterior numuneye.

Burada, çift ortalamalı adım boyutu uyarlamasıyla HMC'yi uyguluyoruz. Ön koşullandırma ve başlatma için bir pilot HMC çalıştırması kullanıyoruz.

Çıkarım, bir GPU'da birkaç dakika içinde çalışır.

3.1 Model için öncelik ve olasılık oluşturma

jd_prior = make_jd_prior(num_countries, num_interventions)
likelihood_fn = make_likelihood_fn(
    intervention_indicators, population_value, deaths,
    infection_fatality_rate, INITIAL_DAYS, TOTAL_DAYS)

3.2 Yardımcı Programlar

def get_bijectors_from_samples(samples, unconstraining_bijectors, batch_axes):
  """Fit bijectors to the samples of a distribution.

  This fits a diagonal covariance multivariate Gaussian transformed by the
  `unconstraining_bijectors` to the provided samples. The resultant
  transformation can be used to precondition MCMC and other inference methods.
  """
  state_std = [    
      tf.math.reduce_std(bij.inverse(x), axis=batch_axes)
      for x, bij in zip(samples, unconstraining_bijectors)
  ]
  state_mu = [
      tf.math.reduce_mean(bij.inverse(x), axis=batch_axes)
      for x, bij in zip(samples, unconstraining_bijectors)
  ]
  return [tfb.Chain([cb, tfb.Shift(sh), tfb.Scale(sc)])
          for cb, sh, sc in zip(unconstraining_bijectors, state_mu, state_std)]

def generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors):
  """Creates an initial MCMC state, and bijectors from the prior."""
  prior_samples = jd_prior.sample(4096)

  bijectors = get_bijectors_from_samples(
      prior_samples, unconstraining_bijectors, batch_axes=0)

  init_state = [
    bij(tf.zeros([nchain] + list(s), DTYPE))
    for s, bij in zip(jd_prior.event_shape, bijectors)
  ]

  return init_state, bijectors

@tf.function(autograph=False, experimental_compile=True)
def sample_hmc(
    init_state,
    step_size,
    target_log_prob_fn,
    unconstraining_bijectors,
    num_steps=500,
    burnin=50,
    num_leapfrog_steps=10):

    def trace_fn(_, pkr):
        return {
            'target_log_prob': pkr.inner_results.inner_results.accepted_results.target_log_prob,
            'diverging': ~(pkr.inner_results.inner_results.log_accept_ratio > -1000.),
            'is_accepted': pkr.inner_results.inner_results.is_accepted,
            'step_size': [tf.exp(s) for s in pkr.log_averaging_step],
        }

    hmc = tfp.mcmc.HamiltonianMonteCarlo(
        target_log_prob_fn,
        step_size=step_size,
        num_leapfrog_steps=num_leapfrog_steps)

    hmc = tfp.mcmc.TransformedTransitionKernel(
        inner_kernel=hmc,
        bijector=unconstraining_bijectors)

    hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
        hmc,
        num_adaptation_steps=int(burnin * 0.8),
        target_accept_prob=0.8,
        decay_rate=0.5)

    # Sampling from the chain.
    return tfp.mcmc.sample_chain(
        num_results=burnin + num_steps,
        current_state=init_state,
        kernel=hmc,
        trace_fn=trace_fn)

3.3 Olay alanı bijektörlerini tanımlayın

İzotropik değişkenli Gauss dağılımı yöntemiyle yapılabilir HMC en verimli ( Mangoubi & Smith (2017) ), birinci aşama mümkün olduğu gibi kadar görünüme hedeflenen yoğunluğa ön-şartlandırma yani.

Her şeyden önce, kısıtlanmış (örn., negatif olmayan) değişkenleri HMC'nin gerektirdiği kısıtlanmamış bir alana dönüştürüyoruz. Ek olarak, dönüştürülmüş hedef yoğunluğun kuyruklarının ağırlığını manipüle etmek için SinhArcsinh bijektörünü kullanıyoruz; bu kadar kabaca düşmek istiyorum \(e^{-x^2}\).

unconstraining_bijectors = [
    tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # tau
    tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # initial_cases
    tfb.Softplus(), # psi
    tfb.Softplus(), # kappa
    tfb.Softplus(), # mu
    tfb.Chain([tfb.Scale(tf.constant(0.4, DTYPE)), tfb.Softplus(),
                tfb.SinhArcsinh(skewness=tf.constant(-0.2, DTYPE), tailweight=tf.constant(2., DTYPE))]), # alpha
    tfb.Softplus(), # ifr_noise
]

3.4 HMC pilot çalışması

İlk önce, dönüştürülmüş uzayda 0'lardan başlatılan önceki tarafından ön koşullandırılmış HMC'yi çalıştırırız. Zinciri başlatmak için önceki örnekleri kullanmıyoruz, çünkü bunlar pratikte zayıf sayısallar nedeniyle zincirlerin sıkışmasına neden oluyor.

%%time

nchain = 32

target_log_prob_fn = lambda *x: jd_prior.log_prob(*x) + likelihood_fn(*x)
init_state, bijectors = generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors)

# Each chain gets its own step size.
step_size = [tf.fill([nchain] + [1] * (len(s.shape) - 1), tf.constant(0.01, DTYPE)) for s in init_state]

burnin = 200
num_steps = 100

pilot_samples, pilot_sampler_stat = sample_hmc(
    init_state,
    step_size,
    target_log_prob_fn,
    bijectors,
    num_steps=num_steps,
    burnin=burnin,
    num_leapfrog_steps=10)

CPU times: user 56.8 s, sys: 2.34 s, total: 59.1 s
Wall time: 1min 1s

3.5 Pilot örnekleri görselleştirin

Sıkışmış zincirler ve göz küresi yakınsama arıyoruz. Burada resmi teşhisler yapabiliriz, ancak bu sadece bir pilot çalışma olduğu için çok gerekli değil.

import arviz as az
az.style.use('arviz-darkgrid')

var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']

pilot_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
                     for k, v in zip(var_name, pilot_samples)}

Isınma sırasında sapmaları gözlemleriz, çünkü öncelikle ikili ortalama adım boyutu uyarlaması, optimal adım boyutu için çok agresif bir arama kullanır. Adaptasyon kapandığında, farklılıklar da ortadan kalkar.

az_trace = az.from_dict(posterior=pilot_with_warmup,
                        sample_stats={'diverging': np.swapaxes(pilot_sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));

png

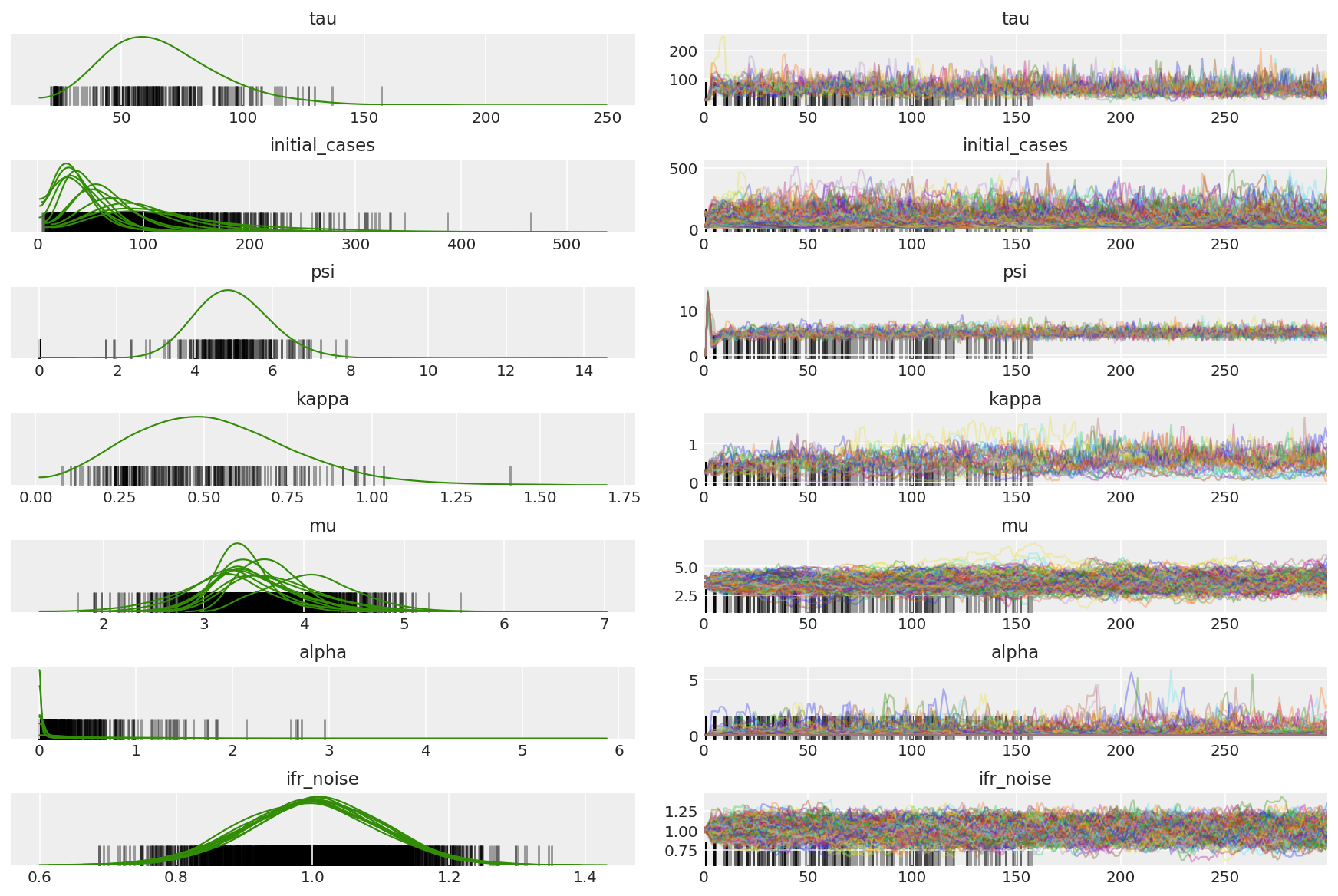
plt.plot(pilot_sampler_stat['step_size'][0]);

png

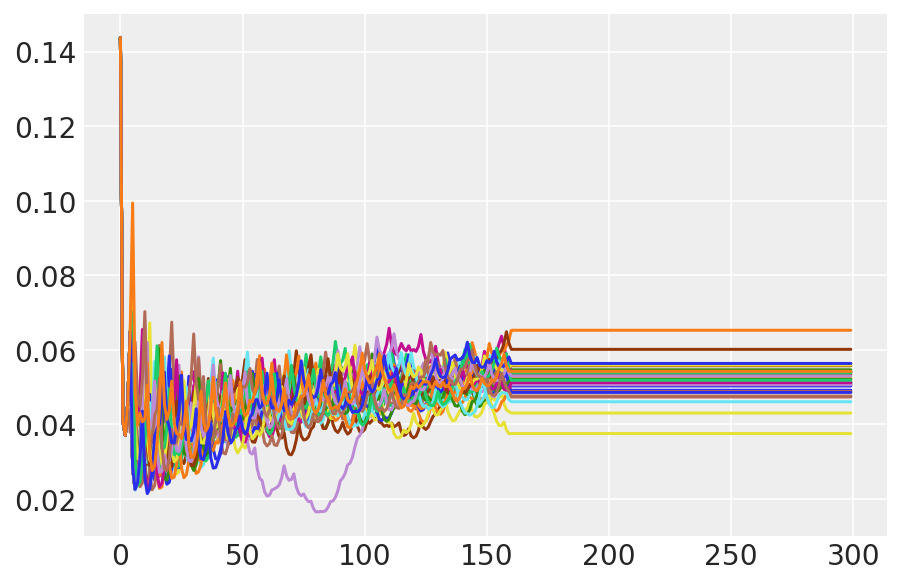
3.6 HMC'yi Çalıştır

Prensipte pilot numuneleri son analiz için kullanabiliriz (eğer yakınsama elde etmek için daha uzun süre çalıştırırsak), ancak bu sefer ön koşullandırılmış ve pilot numunelerle başlatılmış başka bir HMC çalıştırmasını başlatmak biraz daha verimlidir.

%%time

burnin = 50
num_steps = 200

bijectors = get_bijectors_from_samples([s[burnin:] for s in pilot_samples],
                                       unconstraining_bijectors=unconstraining_bijectors,
                                       batch_axes=(0, 1))

samples, sampler_stat = sample_hmc(
    [s[-1] for s in pilot_samples],
    [s[-1] for s in pilot_sampler_stat['step_size']],
    target_log_prob_fn,
    bijectors,
    num_steps=num_steps,
    burnin=burnin,
    num_leapfrog_steps=20)

CPU times: user 1min 26s, sys: 3.88 s, total: 1min 30s
Wall time: 1min 32s

plt.plot(sampler_stat['step_size'][0]);

png

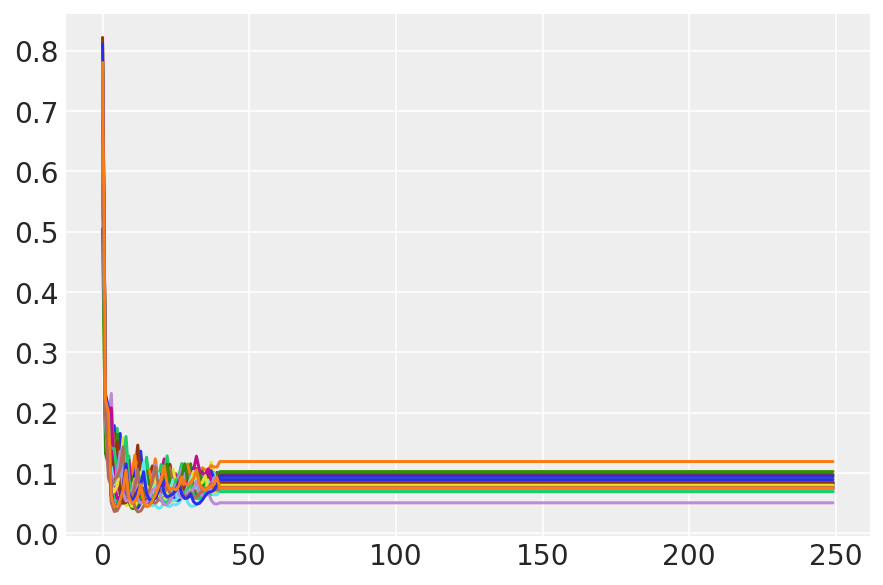
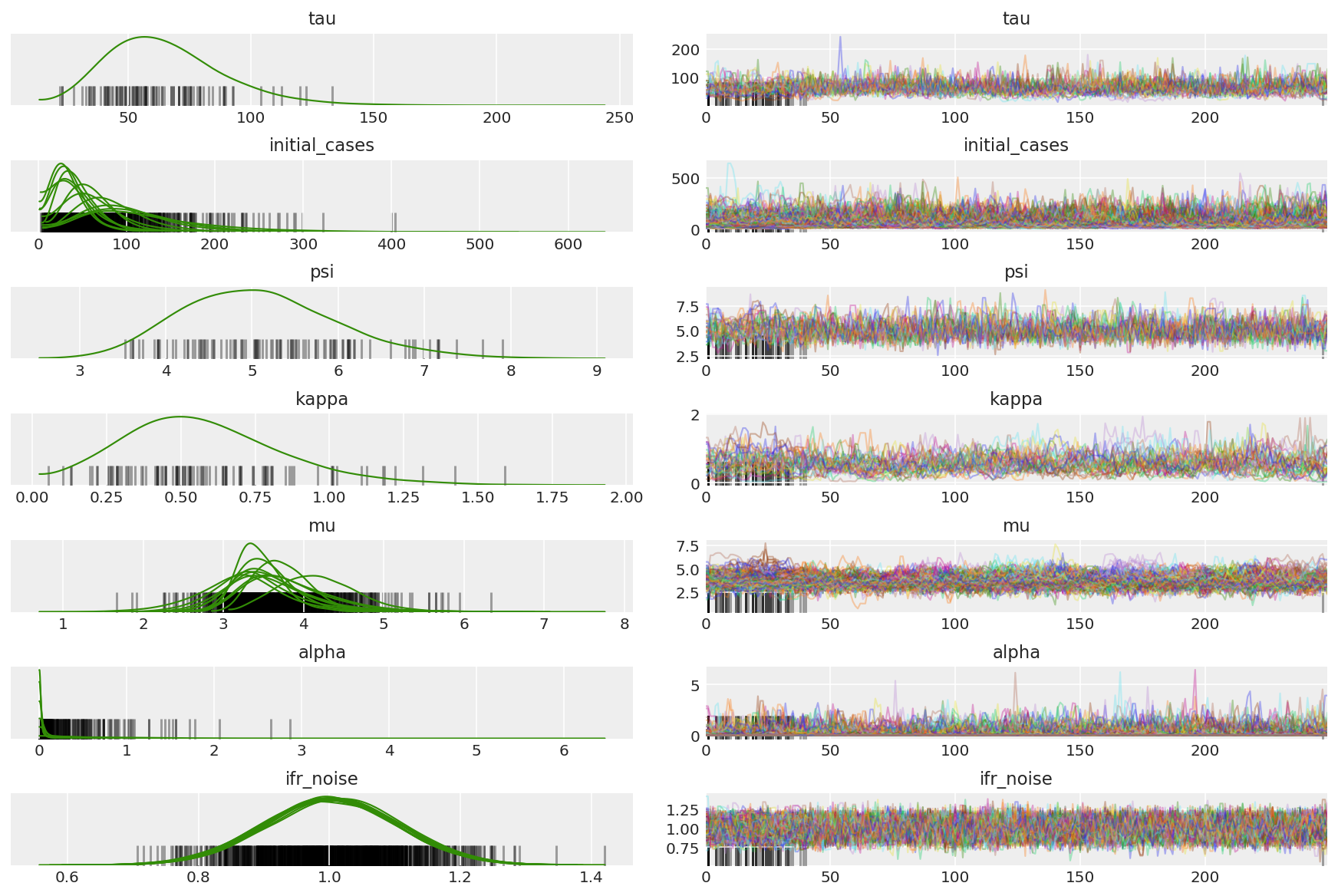
3.7 Örnekleri görselleştirin

import arviz as az
az.style.use('arviz-darkgrid')

var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']

posterior = {k: np.swapaxes(v.numpy()[burnin:], 1, 0)
             for k, v in zip(var_name, samples)}
posterior_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
             for k, v in zip(var_name, samples)}

Zincirlerin özetini hesaplayın. 1'e yakın yüksek ESS ve r_hat arıyoruz.

az.summary(posterior)

az_trace = az.from_dict(posterior=posterior_with_warmup,
                        sample_stats={'diverging': np.swapaxes(sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));

png

Tüm boyutlar arasında otomatik korelasyon fonksiyonlarına bakmak öğreticidir. Hızlı bir şekilde azalan, ancak negatife gidecek kadar fazla olmayan (bu, HMC'nin ergodiklik için kötü olan ve yanlılığa neden olabilecek bir rezonansa ulaştığının göstergesidir) işlevler arıyoruz.

with az.rc_context(rc={'plot.max_subplots': None}):
  az.plot_autocorr(posterior, combined=True, figsize=(12, 16), textsize=12);

png

4 Sonuç

Aşağıdaki grafikler üzerinde arka öngörü dağılımlar incelendiğinde \(R_t\), ölümlerin sayısı ve Flaxman ark analizine benzer enfeksiyonlara sayısına. (2020).

total_num_samples = np.prod(posterior['mu'].shape[:2])

# Calculate R_t given parameter estimates.
def rt_samples_batched(mu, intervention_indicators, alpha):
  linear_prediction = tf.reduce_sum(
      intervention_indicators * alpha[..., np.newaxis, np.newaxis, :], axis=-1)
  rt_hat = mu[..., tf.newaxis] * tf.exp(-linear_prediction, name='rt')
  return rt_hat

alpha_hat = tf.convert_to_tensor(
    posterior['alpha'].reshape(total_num_samples, posterior['alpha'].shape[-1]))
mu_hat = tf.convert_to_tensor(
    posterior['mu'].reshape(total_num_samples, num_countries))
rt_hat = rt_samples_batched(mu_hat, intervention_indicators, alpha_hat)
sampled_initial_cases = posterior['initial_cases'].reshape(
    total_num_samples, num_countries)
sampled_ifr_noise = posterior['ifr_noise'].reshape(
    total_num_samples, num_countries)
psi_hat = posterior['psi'].reshape([total_num_samples])

conv_serial_interval = make_conv_serial_interval(INITIAL_DAYS, TOTAL_DAYS)
conv_fatality_rate = make_conv_fatality_rate(infection_fatality_rate, TOTAL_DAYS)
pred_hat = predict_infections(
    intervention_indicators, population_value, sampled_initial_cases, mu_hat,
    alpha_hat, conv_serial_interval, INITIAL_DAYS, TOTAL_DAYS)
expected_deaths = predict_deaths(pred_hat, sampled_ifr_noise, conv_fatality_rate)

psi_m = psi_hat[np.newaxis, ..., np.newaxis]
probs = tf.clip_by_value(expected_deaths / (expected_deaths + psi_m), 1e-9, 1.)
predicted_deaths = tfd.NegativeBinomial(
    total_count=psi_m, probs=probs).sample()

# Predict counterfactual infections/deaths in the absence of interventions
no_intervention_infections = predict_infections(
    intervention_indicators,
    population_value,
    sampled_initial_cases,
    mu_hat,
    tf.zeros_like(alpha_hat),
    conv_serial_interval,
    INITIAL_DAYS, TOTAL_DAYS)

no_intervention_expected_deaths = predict_deaths(
    no_intervention_infections, sampled_ifr_noise, conv_fatality_rate)
probs = tf.clip_by_value(
    no_intervention_expected_deaths / (no_intervention_expected_deaths + psi_m),
    1e-9, 1.)
no_intervention_predicted_deaths = tfd.NegativeBinomial(
    total_count=psi_m, probs=probs).sample()

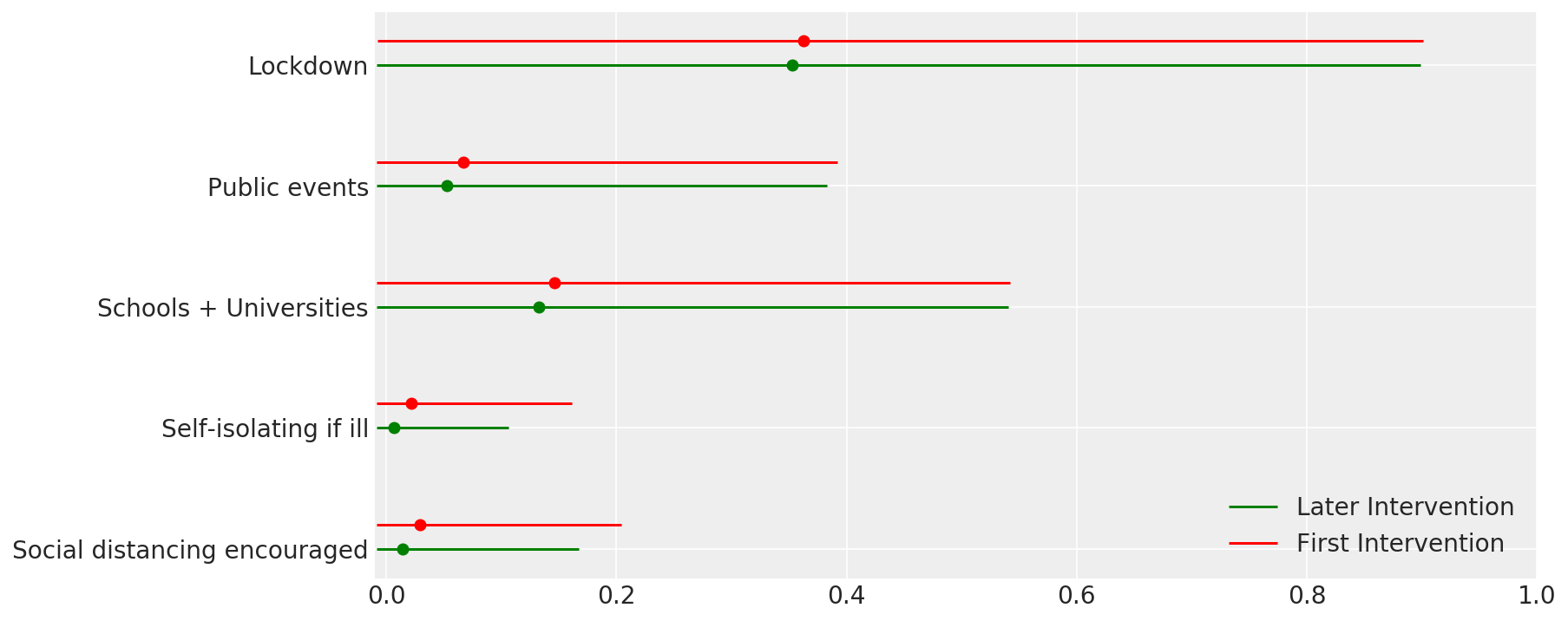
4.1 Müdahalelerin etkinliği

Flaxman ve ark.'nın Şekil 4'üne benzer. (2020).

def intervention_effectiveness(alpha):

  alpha_adj = 1. - np.exp(-alpha + np.log(1.05) / 6.)
  alpha_adj_first = (
      1. - np.exp(-alpha - alpha[..., -1:] + np.log(1.05) / 6.))

  fig, ax = plt.subplots(1, 1, figsize=[12, 6])
  intervention_perm = [2, 1, 3, 4, 0]
  percentile_vals = [2.5, 97.5]
  jitter = .2

  for ind in range(5):
    first_low, first_high = tfp.stats.percentile(
        alpha_adj_first[..., ind], percentile_vals)
    low, high = tfp.stats.percentile(
        alpha_adj[..., ind], percentile_vals)

    p_ind = intervention_perm[ind]
    ax.hlines(p_ind, low, high, label='Later Intervention', colors='g')
    ax.scatter(alpha_adj[..., ind].mean(), p_ind, color='g')
    ax.hlines(p_ind + jitter, first_low, first_high,
              label='First Intervention', colors='r')
    ax.scatter(alpha_adj_first[..., ind].mean(), p_ind + jitter, color='r')

    if ind == 0:
      plt.legend(loc='lower right')
  ax.set_yticks(range(5))
  ax.set_yticklabels(
      [any_intervention_list[intervention_perm.index(p)] for p in range(5)])
  ax.set_xlim([-0.01, 1.])
  r = fig.patch
  r.set_facecolor('white') 

intervention_effectiveness(alpha_hat)

png

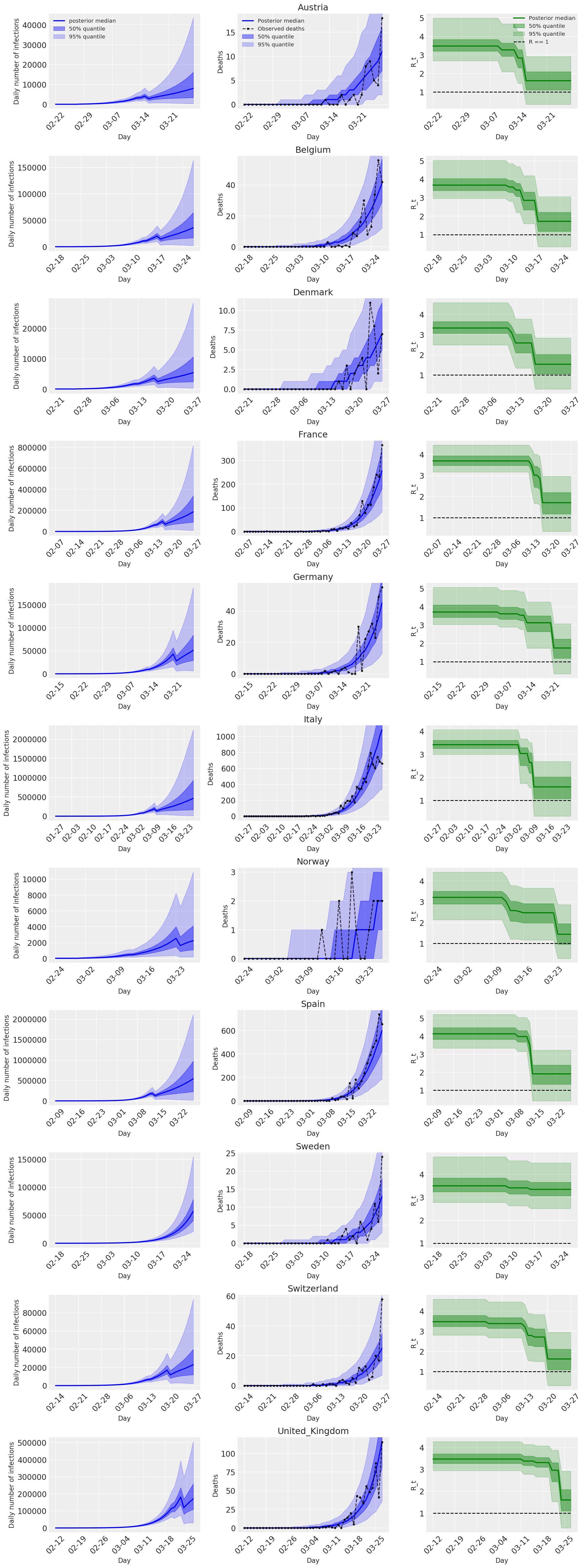
4.2 Ülkeye göre enfeksiyonlar, ölümler ve R_t

Flaxman ve ark.'nın Şekil 2'sine benzer. (2020).

png

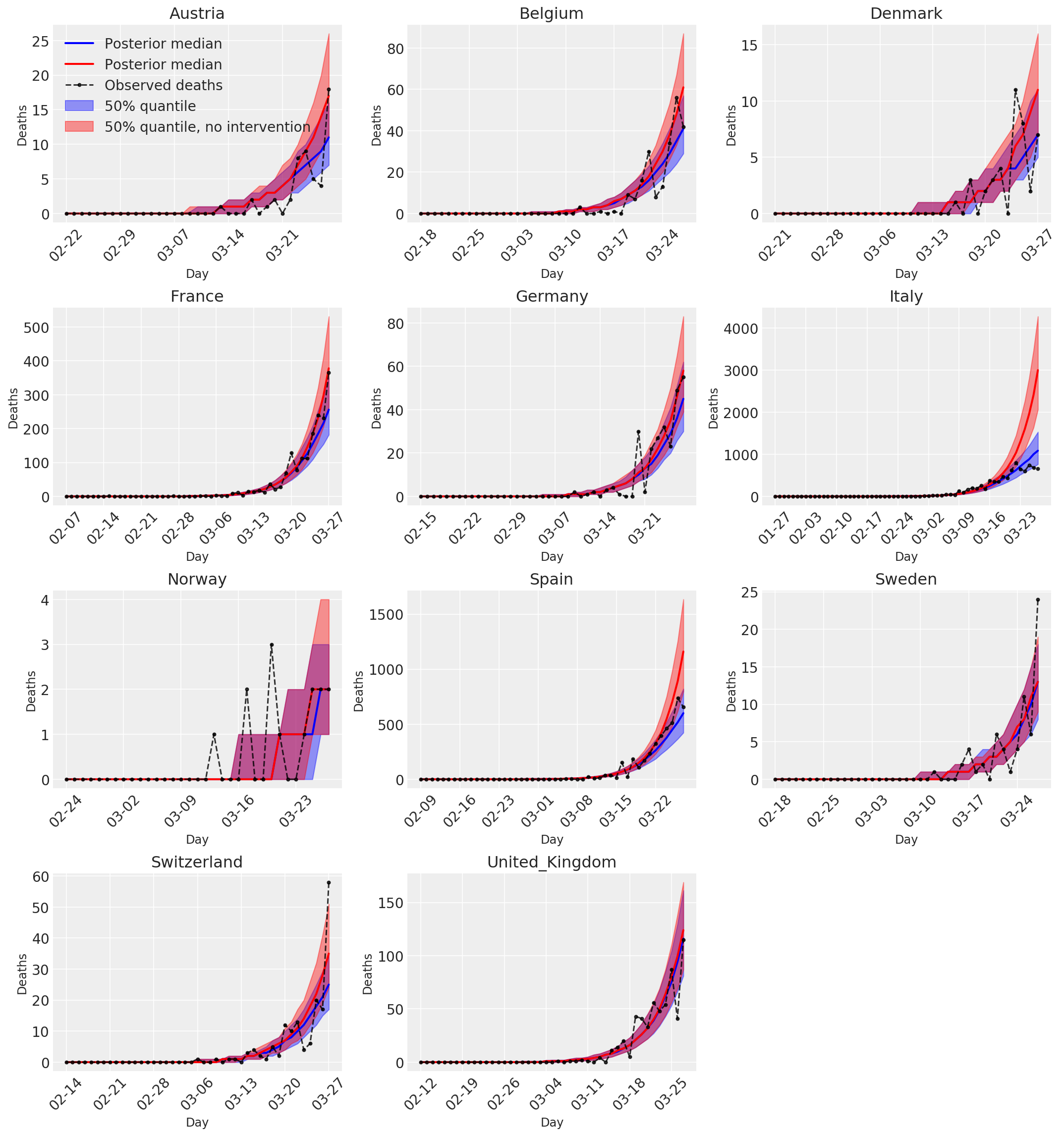
4.3 Müdahaleli ve müdahalesiz günlük tahmini/tahmin edilen ölüm sayısı

png