 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Bir [bağ] (https://en.wikipedia.org/wiki/Copula_ (probability_theory% 29) rastgele değişkenler arasındaki bağımlılığın yakalamak için klasik bir yaklaşımdır. Daha biçimsel olarak, bir bağ, bir çok değişkenli dağılımıdır \(C(U_1, U_2, ...., U_n)\) marjinalleştirme şekilde verir \(U_i \sim \text{Uniform}(0, 1)\).
Copulalar ilginçtir çünkü onları keyfi marjinallerle çok değişkenli dağılımlar oluşturmak için kullanabiliriz. Tarif bu:
- Kullanarak olasılık integrali Transform döner rasgele bir sürekli RV \(X\) muntazam bir içine \(F_X(X)\), \(F_X\) KTL olan \(X\).
- Bir bağ (diyelim iki değişkenli) Verilen \(C(U, V)\), biz buna sahip \(U\) ve \(V\) üniforma marjinal dağılımları vardır.
- Şimdi bizim RV ilgi var verilen \(X, Y\)yeni bir dağıtım oluşturmak, \(C'(X, Y) = C(F_X(X), F_Y(Y))\). İçin marjinal ilan \(X\) ve \(Y\) biz arzu olanlardır.
Marjinaller tek değişkenlidir ve bu nedenle ölçülmesi ve/veya modellenmesi daha kolay olabilir. Bir kopula, marjinallerden başlamayı ve aynı zamanda boyutlar arasında keyfi bir korelasyon elde etmeyi sağlar.
Gauss Kopulası
Kopulaların nasıl oluşturulduğunu göstermek için, çok değişkenli Gauss korelasyonlarına göre bağımlılığı yakalama durumunu düşünün. Bir Gauss Copula vermiş olduğu \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) \(\Phi_\Sigma\) kovaryans ile, bir MultivariateNormal ait CDF temsil \(\Sigma\) ortalama 0 ve \(\Phi^{-1}\) standart normal için ters CDF olup.
Normalin ters CDF'sini uygulamak, normal olarak dağıtılacak tek biçimli boyutları çarpıtır. Çok değişkenli normalin CDF'sini uygulamak, dağılımı marjinal olarak tek biçimli ve Gauss korelasyonlarıyla eziyor.
Böylece ne olsun Gauss Kapula birim hiperküp üzerinde bir dağıtım olmasıdır \([0, 1]^n\) üniforma marjinaller ile.
Gibi tanımlanmıştır, Gauss Copula ile uygulanabilir tfd.TransformedDistribution ve uygun Bijector . Yani, biz uyguladığı Normal dağılım en CDF'nin ters kullanımı yoluyla bir MultivariateNormal dönüştüren olduğunu tfb.NormalCDF bijector.
Aşağıda, bir basitleştirilmesi varsayımı ile Gauss Kapula uygulamak: kovaryans (dolayısıyla bir kovaryans bir Choleskey faktörü parametreli olduğu MultivariateNormalTriL ). (Bir diğer kullanabilir tf.linalg.LinearOperators farklı matris içermeyen varsayımlar kodlamak.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
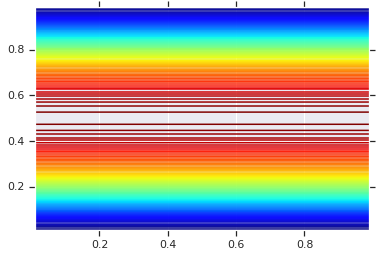
Bununla birlikte, böyle bir modelden gelen güç, kopulayı keyfi RV'lerde kullanmak için Olasılık İntegral Dönüşümünü kullanmaktır.
Bir modelle başlıyoruz:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
ve iki değişkenli RV almak için copula kullanmak \(Z\)marjinaller vardır Kumaraswamy ve Gumbel'ı .
Bu iki RV tarafından üretilen ürün dağılımını çizerek başlayacağız. Bu sadece Copula'yı uyguladığımız zaman için bir karşılaştırma noktası olarak hizmet etmek içindir.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
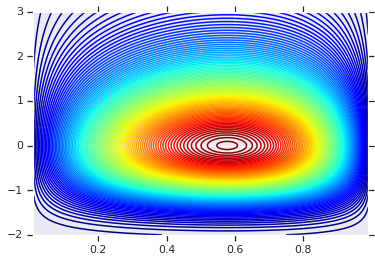
Farklı Marjinallerle Ortak Dağıtım
Şimdi dağılımları birleştirmek için bir Gauss kopulası kullanıyoruz ve bunu çiziyoruz. Yine seçim bizim aracıdır TransformedDistribution uygun uygulayarak Bijector seçilen marjinaller elde etmek.
Spesifik olarak, bir kullanma Blockwise (hala bir örten dönüşüm olan) vektörün farklı bölgelerinde farklı bijectors geçerlidir bijector.
Artık istediğimiz Copula'yı tanımlayabiliriz. Hedef marjinallerin (bijektör olarak kodlanmış) bir listesi verildiğinde, kopulayı kullanan ve belirtilen marjinallere sahip yeni bir dağıtım kolayca oluşturabiliriz.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
Son olarak, bu Gauss Copula'sını gerçekten kullanalım. Biz bir Cholesky kullanacağız \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\)1 sapmalar karşılık gelecektir, ve korelasyon \(\rho\) değişkenli normal için.
Birkaç duruma bakacağız:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
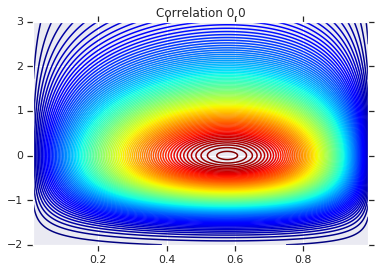
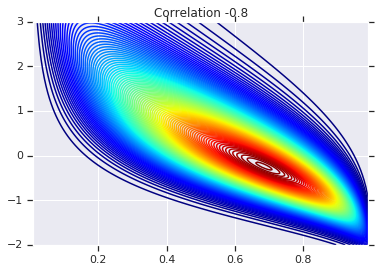
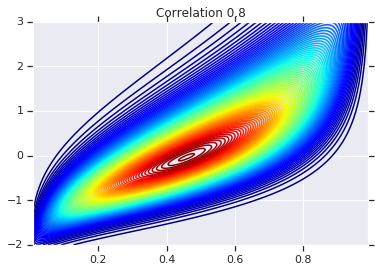
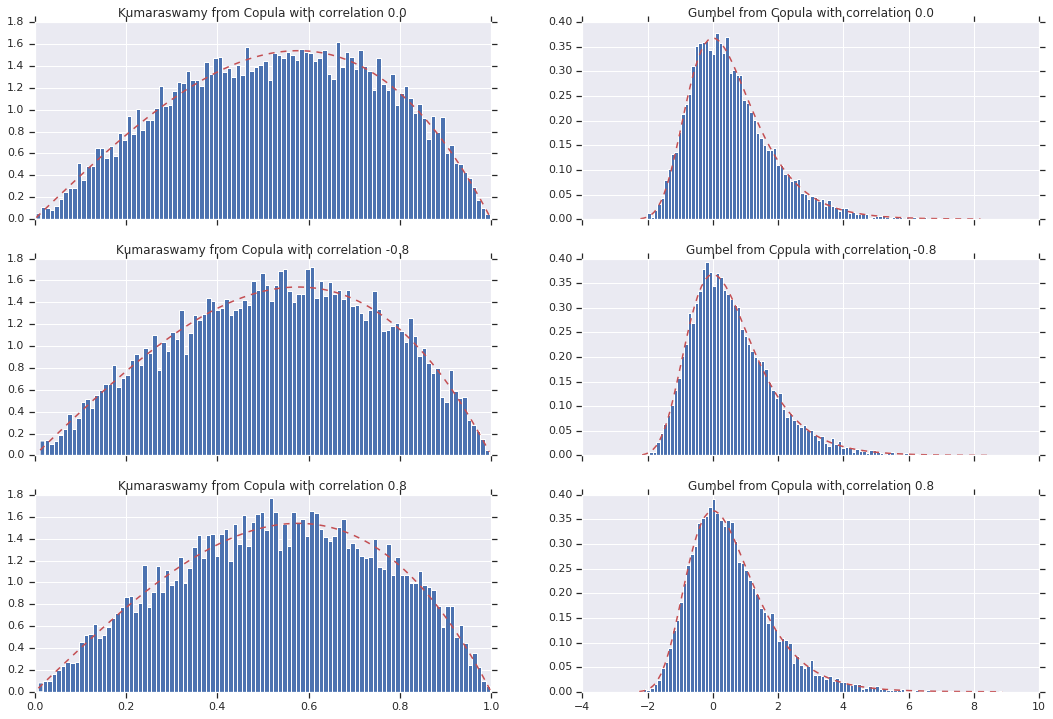
Son olarak, gerçekten istediğimiz marjinalleri elde ettiğimizi doğrulayalım.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
Çözüm
Ve işte başlıyoruz! Biz kullanarak Gauss Kapulalar kurulabileceğini göstermiş Bijector API.
Daha genel olarak bijectors kullanarak yazma Bijector esnek modelleme için dağılımların zengin aileleri oluşturabilir, API ve bir dağılımla bunları meydana.
