 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Bu ortak çalışmada, TensorFlow ve TensorFlow Probability kullanarak Gauss süreç regresyonunu keşfediyoruz. Bilinen bazı fonksiyonlardan bazı gürültülü gözlemler üretiyoruz ve GP modellerini bu verilere uyduruyoruz. Daha sonra GP posteriorundan örnek alırız ve örneklenen fonksiyon değerlerini kendi etki alanlarındaki ızgaralar üzerinde çizeriz.
Arka plan
Let \(\mathcal{X}\) herhangi kümesi olsun. Bir Gauss işlemi (GP) tarafından indekslenen rastgele değişkenin bir koleksiyon \(\mathcal{X}\) örneğin eğer\(\{X_1, \ldots, X_n\} \subset \mathcal{X}\) bir sonlu bir alt kümesi, marjinal yoğunluk\(p(X_1 = x_1, \ldots, X_n = x_n)\) olan çok değişkenli Gauss. Herhangi bir Gauss dağılımı, tamamen birinci ve ikinci merkezi momentleri (ortalama ve kovaryans) tarafından belirlenir ve GP'ler istisna değildir. Biz onun ortalama işlevi açısından tamamen GP belirtebilirsiniz \(\mu : \mathcal{X} \to \mathbb{R}\) ve kovaryans fonksiyonu\(k : \mathcal{X} \times \mathcal{X} \to \mathbb{R}\). GP'lerin ifade gücünün çoğu, kovaryans fonksiyonunun seçiminde kapsüllenmiştir. Çeşitli nedenlerle, kovaryans fonksiyonu da bir çekirdek fonksiyonu olarak adlandırılır. Sadece (bakınız simetrik ve pozitif tanımlı olması gerekmektedir Ch. Rasmussen ve Williams 4 ). Aşağıda ExponentiatedQuadratic kovaryans çekirdeğini kullanıyoruz. onun formu
\[ k(x, x') := \sigma^2 \exp \left( \frac{\|x - x'\|^2}{\lambda^2} \right) \]
burada \(\sigma^2\) 'amplitüd' ve adı \(\lambda\) uzunluk ölçeği. Çekirdek parametreleri, bir maksimum olabilirlik optimizasyon prosedürü ile seçilebilir.
Bir GP tam bir numune, tüm alanı üzerinde gerçek değerli fonksiyonu içerir\(\mathcal{X}\) ve gerçekleştirmek için pratik uygulamada olduğu; genellikle bir numuneyi gözlemlemek için bir dizi nokta seçer ve bu noktalarda fonksiyon değerleri çizer. Bu, uygun (sonlu boyutlu) çok değişkenli bir Gauss'tan örnekleme yoluyla elde edilir.
Yukarıdaki tanıma göre, herhangi bir sonlu boyutlu çok değişkenli Gauss dağılımının da bir Gauss süreci olduğuna dikkat edin. Tek bir GP atıfta zaman indeks kümesi bazı olduğunu Genellikle, Eğer örtülü bir \(\mathbb{R}^n\)ve biz gerçekten burada bu varsayımı yapacaktır.
Gauss süreçlerinin makine öğreniminde yaygın bir uygulaması Gauss süreç regresyonudur. Fikir Bize verilen gürültülü gözlemler bilinmeyen bir fonksiyonu tahmin etmek istemesi gelmektedir \(\{y_1, \ldots, y_N\}\) noktalarının sonlu sayıda işlevin \(\{x_1, \ldots x_N\}.\) Biz üretici sürecini hayal
\[ \begin{align} f \sim \: & \textsf{GaussianProcess}\left( \text{mean_fn}=\mu(x), \text{covariance_fn}=k(x, x')\right) \\ y_i \sim \: & \textsf{Normal}\left( \text{loc}=f(x_i), \text{scale}=\sigma\right), i = 1, \ldots, N \end{align} \]
Yukarıda belirtildiği gibi, sonsuz sayıda noktada değerine ihtiyaç duyacağımız için örneklenen fonksiyonun hesaplanması imkansızdır. Bunun yerine, çok değişkenli bir Gauss'tan sonlu bir örnek düşünülür.
\[ \begin{gather} \begin{bmatrix} f(x_1) \\ \vdots \\ f(x_N) \end{bmatrix} \sim \textsf{MultivariateNormal} \left( \: \text{loc}= \begin{bmatrix} \mu(x_1) \\ \vdots \\ \mu(x_N) \end{bmatrix} \:,\: \text{scale}= \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix}^{1/2} \: \right) \end{gather} \\ y_i \sim \textsf{Normal} \left( \text{loc}=f(x_i), \text{scale}=\sigma \right) \]
Üs Not \(\frac{1}{2}\) kovaryans matrisi üzerinde: Bu Cholesky ayrışma belirtmektedir. MVN, konum ölçeğinde bir aile dağılımı olduğu için Cholesky'nin hesaplanması gereklidir. Maalesef Choleskey çözümleme alarak hesaplama pahalı \(O(N^3)\) zaman ve \(O(N^2)\) alanı. GP literatürünün çoğu, bu görünüşte zararsız küçük üsle uğraşmaya odaklanmıştır.
Önceden ortalama fonksiyonunun sabit, genellikle sıfır olarak alınması yaygındır. Ayrıca, bazı gösterim kuralları uygundur. Bir çoğu yazar \(\mathbf{f}\) örneklenmiş fonksiyon değerleri sonlu vektör. İlginç gösterimler arasında bir sayı uygulanması ile elde edilen kovaryans matrisi için kullanılan \(k\) girişlerin çiftlerine. Aşağıdaki (Quiñonero-Candela'nin 2005) , matriks bileşenlerinin, özellikle giriş noktalarında fonksiyon değerlerinin kovaryanslar olduğuna dikkat edilmelidir. Olarak Böylece kovaryans matrisi de isim verebilir \(K_{AB}\)burada \(A\) ve \(B\) verilen matris boyutları boyunca fonksiyon değerleri toplanması bazı göstergeler vardır.
Örneğin, belirli bir gözlemlenmiş \((\mathbf{x}, \mathbf{y})\) ima gizli fonksiyon değerleri ile \(\mathbf{f}\), yazabiliriz
\[ K_{\mathbf{f},\mathbf{f} } = \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix} \]
Benzer şekilde, aşağıdaki gibi girdi setlerini karıştırabiliriz.
\[ K_{\mathbf{f},*} = \begin{bmatrix} k(x_1, x^*_1) & \cdots & k(x_1, x^*_T) \\ \vdots & \ddots & \vdots \\ k(x_N, x^*_1) & \cdots & k(x_N, x^*_T) \\ \end{bmatrix} \]
biz varsayalım nerede vardır \(N\) eğitim girdileri ve \(T\) testi girdiler. Yukarıdaki üretken süreç daha sonra kompakt bir şekilde şu şekilde yazılabilir:
\[ \begin{align} \mathbf{f} \sim \: & \textsf{MultivariateNormal} \left( \text{loc}=\mathbf{0}, \text{scale}=K_{\mathbf{f},\mathbf{f} }^{1/2} \right) \\ y_i \sim \: & \textsf{Normal} \left( \text{loc}=f_i, \text{scale}=\sigma \right), i = 1, \ldots, N \end{align} \]
İlk satırında Numune alma işlemi sınırlı bir kümesini elde edilir \(N\) GP yukarıda çizmek gösterimde olarak değil tüm işlev - çok değişkenli bir Gauss gelen fonksiyon değerleri. İkinci satır, bir koleksiyon tarif \(N\) tek değişkenli Gauss çeşitli fonksiyon değerleri ortalanmış gelen sabit gözlem gürültü ile çeken \(\sigma^2\).
Yukarıdaki üretici model yerindeyken, sonsal çıkarım problemini düşünmeye devam edebiliriz. Bu, yukarıdaki süreçten gözlemlenen gürültülü verilere bağlı olarak, yeni bir dizi test noktasında fonksiyon değerleri üzerinde bir posterior dağılım sağlar.
Yerinde yukarıdaki gösterimde ile, kompakt geleceği üzerinde arka öngörü dağılımını yazabilir (gürültülü) gözlemleri (ayrıntılı bilgi için, bir §2.2 bakınız aşağıdaki gibi girdileri ve eğitim verilerini tekabül şartına Rasmussen & Williams ).
\[ \mathbf{y}^* \mid \mathbf{x}^*, \mathbf{x}, \mathbf{y} \sim \textsf{Normal} \left( \text{loc}=\mathbf{\mu}^*, \text{scale}=(\Sigma^*)^{1/2} \right), \]
nerede
\[ \mathbf{\mu}^* = K_{*,\mathbf{f} }\left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} \mathbf{y} \]
ve
\[ \Sigma^* = K_{*,*} - K_{*,\mathbf{f} } \left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} K_{\mathbf{f},*} \]
ithalat
import time
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
tfb = tfp.bijectors
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
tf.enable_v2_behavior()
from mpl_toolkits.mplot3d import Axes3D
%pylab inline
# Configure plot defaults
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['grid.color'] = '#666666'
%config InlineBackend.figure_format = 'png'
Populating the interactive namespace from numpy and matplotlib
Örnek: Gürültülü Sinüzoidal Verilerde Tam GP Regresyonu
Burada gürültülü bir sinüzoidden eğitim verileri oluşturuyoruz, ardından GP regresyon modelinin arkasından bir grup eğriyi örnekliyoruz. Kullandığımız Adam (biz önce altında verilerin negatif log olasılığını en aza indirmek) çekirdek hyperparameters optimize etmek. Eğitim eğrisini, ardından gerçek işlevi ve arka örnekleri çizeriz.
def sinusoid(x):
return np.sin(3 * np.pi * x[..., 0])
def generate_1d_data(num_training_points, observation_noise_variance):
"""Generate noisy sinusoidal observations at a random set of points.
Returns:
observation_index_points, observations
"""
index_points_ = np.random.uniform(-1., 1., (num_training_points, 1))
index_points_ = index_points_.astype(np.float64)
# y = f(x) + noise
observations_ = (sinusoid(index_points_) +
np.random.normal(loc=0,
scale=np.sqrt(observation_noise_variance),
size=(num_training_points)))
return index_points_, observations_
# Generate training data with a known noise level (we'll later try to recover
# this value from the data).
NUM_TRAINING_POINTS = 100
observation_index_points_, observations_ = generate_1d_data(
num_training_points=NUM_TRAINING_POINTS,
observation_noise_variance=.1)
Biz çekirdek hyperparameters üzerinde sabıkası koyun ve kullanan hyperparameters ve gözlenen verilerin ortak dağılımını yazacağım tfd.JointDistributionNamed .
def build_gp(amplitude, length_scale, observation_noise_variance):
"""Defines the conditional dist. of GP outputs, given kernel parameters."""
# Create the covariance kernel, which will be shared between the prior (which we
# use for maximum likelihood training) and the posterior (which we use for
# posterior predictive sampling)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
# Create the GP prior distribution, which we will use to train the model
# parameters.
return tfd.GaussianProcess(
kernel=kernel,
index_points=observation_index_points_,
observation_noise_variance=observation_noise_variance)
gp_joint_model = tfd.JointDistributionNamed({
'amplitude': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'length_scale': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observation_noise_variance': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observations': build_gp,
})
Bir öncekinden örnek alabileceğimizi doğrulayarak uygulamamızı akıl sağlığı açısından kontrol edebilir ve bir örneğin günlük yoğunluğunu hesaplayabiliriz.
x = gp_joint_model.sample()
lp = gp_joint_model.log_prob(x)
print("sampled {}".format(x))
print("log_prob of sample: {}".format(lp))
sampled {'observation_noise_variance': <tf.Tensor: shape=(), dtype=float64, numpy=2.067952217184325>, 'length_scale': <tf.Tensor: shape=(), dtype=float64, numpy=1.154435715487831>, 'amplitude': <tf.Tensor: shape=(), dtype=float64, numpy=5.383850737703549>, 'observations': <tf.Tensor: shape=(100,), dtype=float64, numpy=
array([-2.37070577, -2.05363838, -0.95152824, 3.73509388, -0.2912646 ,
0.46112342, -1.98018513, -2.10295857, -1.33589756, -2.23027226,
-2.25081374, -0.89450835, -2.54196452, 1.46621647, 2.32016193,
5.82399989, 2.27241034, -0.67523432, -1.89150197, -1.39834474,
-2.33954116, 0.7785609 , -1.42763627, -0.57389025, -0.18226098,
-3.45098732, 0.27986652, -3.64532398, -1.28635204, -2.42362875,
0.01107288, -2.53222176, -2.0886136 , -5.54047694, -2.18389607,
-1.11665628, -3.07161217, -2.06070336, -0.84464262, 1.29238438,
-0.64973999, -2.63805504, -3.93317576, 0.65546645, 2.24721181,
-0.73403676, 5.31628298, -1.2208384 , 4.77782252, -1.42978168,
-3.3089274 , 3.25370494, 3.02117591, -1.54862932, -1.07360811,
1.2004856 , -4.3017773 , -4.95787789, -1.95245901, -2.15960839,
-3.78592731, -1.74096185, 3.54891595, 0.56294143, 1.15288455,
-0.77323696, 2.34430694, -1.05302007, -0.7514684 , -0.98321063,
-3.01300144, -3.00033274, 0.44200837, 0.45060886, -1.84497318,
-1.89616746, -2.15647664, -2.65672581, -3.65493379, 1.70923375,
-3.88695218, -0.05151283, 4.51906677, -2.28117003, 3.03032793,
-1.47713194, -0.35625273, 3.73501587, -2.09328047, -0.60665614,
-0.78177188, -0.67298545, 2.97436033, -0.29407932, 2.98482427,
-1.54951178, 2.79206821, 4.2225733 , 2.56265198, 2.80373284])>}
log_prob of sample: -194.96442183797524
Şimdi en yüksek sonsal olasılığa sahip parametre değerlerini bulmak için optimize edelim. Her parametre için bir değişken tanımlayacağız ve değerlerini pozitif olacak şekilde sınırlayacağız.
# Create the trainable model parameters, which we'll subsequently optimize.
# Note that we constrain them to be strictly positive.
constrain_positive = tfb.Shift(np.finfo(np.float64).tiny)(tfb.Exp())
amplitude_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='amplitude',
dtype=np.float64)
length_scale_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='length_scale',
dtype=np.float64)
observation_noise_variance_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='observation_noise_variance_var',
dtype=np.float64)
trainable_variables = [v.trainable_variables[0] for v in
[amplitude_var,
length_scale_var,
observation_noise_variance_var]]
Bizim gözlenen verilere modeli şart için, bir tanımlayacağız target_log_prob (hala anlaşılmaktadır edilecek) çekirdek hyperparameters alır işlevini.
def target_log_prob(amplitude, length_scale, observation_noise_variance):
return gp_joint_model.log_prob({
'amplitude': amplitude,
'length_scale': length_scale,
'observation_noise_variance': observation_noise_variance,
'observations': observations_
})
# Now we optimize the model parameters.
num_iters = 1000
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Use `tf.function` to trace the loss for more efficient evaluation.
@tf.function(autograph=False, jit_compile=False)
def train_model():
with tf.GradientTape() as tape:
loss = -target_log_prob(amplitude_var, length_scale_var,
observation_noise_variance_var)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
# Store the likelihood values during training, so we can plot the progress
lls_ = np.zeros(num_iters, np.float64)
for i in range(num_iters):
loss = train_model()
lls_[i] = loss
print('Trained parameters:')
print('amplitude: {}'.format(amplitude_var._value().numpy()))
print('length_scale: {}'.format(length_scale_var._value().numpy()))
print('observation_noise_variance: {}'.format(observation_noise_variance_var._value().numpy()))
Trained parameters: amplitude: 0.9176153445125278 length_scale: 0.18444082442910079 observation_noise_variance: 0.0880273312850989
# Plot the loss evolution
plt.figure(figsize=(12, 4))
plt.plot(lls_)
plt.xlabel("Training iteration")
plt.ylabel("Log marginal likelihood")
plt.show()

# Having trained the model, we'd like to sample from the posterior conditioned
# on observations. We'd like the samples to be at points other than the training
# inputs.
predictive_index_points_ = np.linspace(-1.2, 1.2, 200, dtype=np.float64)
# Reshape to [200, 1] -- 1 is the dimensionality of the feature space.
predictive_index_points_ = predictive_index_points_[..., np.newaxis]
optimized_kernel = tfk.ExponentiatedQuadratic(amplitude_var, length_scale_var)
gprm = tfd.GaussianProcessRegressionModel(
kernel=optimized_kernel,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_var,
predictive_noise_variance=0.)
# Create op to draw 50 independent samples, each of which is a *joint* draw
# from the posterior at the predictive_index_points_. Since we have 200 input
# locations as defined above, this posterior distribution over corresponding
# function values is a 200-dimensional multivariate Gaussian distribution!
num_samples = 50
samples = gprm.sample(num_samples)
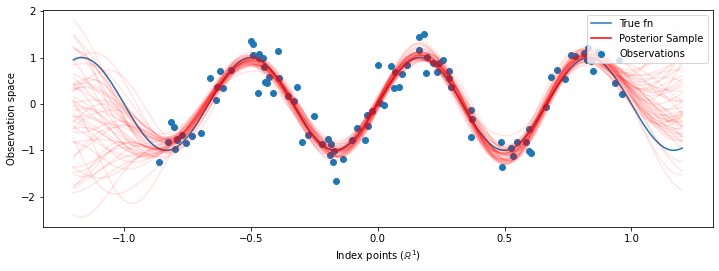
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
HMC ile hiperparametreleri marjinalleştirme
Hiperparametreleri optimize etmek yerine, onları Hamiltonian Monte Carlo ile entegre etmeyi deneyelim. İlk olarak, gözlemler göz önüne alındığında, çekirdek hiperparametreleri üzerinden sonsal dağılımdan yaklaşık olarak çizmek için bir örnekleyici tanımlayacak ve çalıştıracağız.
num_results = 100
num_burnin_steps = 50
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=target_log_prob,
step_size=tf.cast(0.1, tf.float64)),
bijector=[constrain_positive, constrain_positive, constrain_positive])
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=tf.cast(0.75, tf.float64))
initial_state = [tf.cast(x, tf.float64) for x in [1., 1., 1.]]
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=False)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=lambda current_state, kernel_results: kernel_results)
t0 = time.time()
samples, kernel_results = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 9.00s.
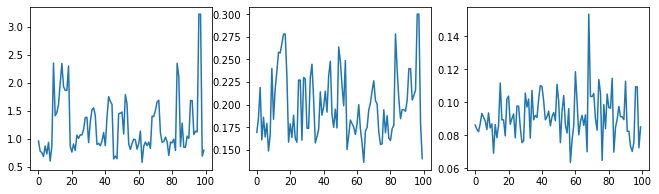
Hiperparametre izlerini inceleyerek örnekleyiciyi akıl sağlığı açısından kontrol edelim.
(amplitude_samples,
length_scale_samples,
observation_noise_variance_samples) = samples
f = plt.figure(figsize=[15, 3])
for i, s in enumerate(samples):
ax = f.add_subplot(1, len(samples) + 1, i + 1)
ax.plot(s)
Şimdi yerine optimize hyperparameters ile tek GP oluşturmanın, biz GP karışımı, hyperparameters üzerinde arka dağılımından bir örnek tarafından tanımlanan her şekilde arka öngörü dağılımını oluşturmak. Bu, gözlemlenmeyen konumlardaki marjinal tahmine dayalı dağılımı hesaplamak için Monte Carlo örneklemesi yoluyla sonsal parametreler üzerinden yaklaşık olarak bütünleşir.
# The sampled hyperparams have a leading batch dimension, `[num_results, ...]`,
# so they construct a *batch* of kernels.
batch_of_posterior_kernels = tfk.ExponentiatedQuadratic(
amplitude_samples, length_scale_samples)
# The batch of kernels creates a batch of GP predictive models, one for each
# posterior sample.
batch_gprm = tfd.GaussianProcessRegressionModel(
kernel=batch_of_posterior_kernels,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_samples,
predictive_noise_variance=0.)
# To construct the marginal predictive distribution, we average with uniform
# weight over the posterior samples.
predictive_gprm = tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(logits=tf.zeros([num_results])),
components_distribution=batch_gprm)
num_samples = 50
samples = predictive_gprm.sample(num_samples)
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
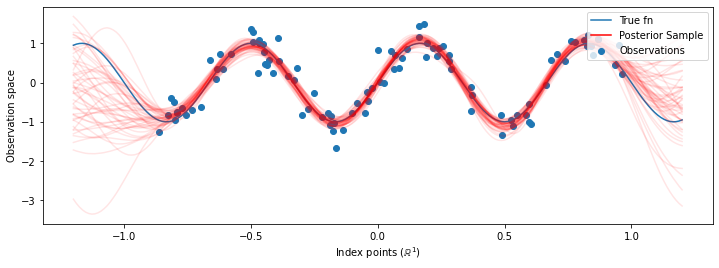
Bu durumda farklılıklar ince olsa da, genel olarak, sonsal öngörücü dağılımın, yukarıda yaptığımız gibi yalnızca en olası parametreleri kullanmaktan daha iyi genellemesini (uzak verilere daha yüksek olasılık vermesini) bekleriz.
