 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
Installare
TF_Installation = 'System'
if TF_Installation == 'TF Nightly':
!pip install -q --upgrade tf-nightly
print('Installation of `tf-nightly` complete.')
elif TF_Installation == 'TF Stable':
!pip install -q --upgrade tensorflow
print('Installation of `tensorflow` complete.')
elif TF_Installation == 'System':
pass
else:
raise ValueError('Selection Error: Please select a valid '
'installation option.')
Installare
TFP_Installation = "System"
if TFP_Installation == "Nightly":
!pip install -q tfp-nightly
print("Installation of `tfp-nightly` complete.")
elif TFP_Installation == "Stable":
!pip install -q --upgrade tensorflow-probability
print("Installation of `tensorflow-probability` complete.")
elif TFP_Installation == "System":
pass
else:
raise ValueError("Selection Error: Please select a valid "
"installation option.")
Astratto
In questa collaborazione dimostriamo come adattare un modello lineare generalizzato a effetti misti utilizzando l'inferenza variazionale in TensorFlow Probability.
Famiglia di modelli
Generalizzata lineare modelli misti effetto (GLMM) sono simili a generalizzata lineare modelli (GLM) tranne che incorporano un rumore specifico campione in risposta lineare prevista. Ciò è utile in parte perché consente alle funzionalità viste raramente di condividere le informazioni con le funzionalità viste più comunemente.
Come processo generativo, un Modello Lineare Generalizzato a Effetti Misti (GLMM) è caratterizzato da:
\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]
dove:
\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]
In altre parole, questo dice che ogni categoria di ogni gruppo è associato con un campione, \(\beta_{rc}\), da un normale multivariata. Anche se la \(\beta_{rc}\) attinge sono sempre indipendenti, sono solo indentically distribuiti per un gruppo \(r\): avviso non v'è esattamente un \(\Sigma_r\) per ogni \(r\in\{1,\ldots,R\}\).
Quando affinely unito con le caratteristiche del gruppo di un campione (\(z_{r,i}\)), il risultato è rumore di esempio specifico sul \(i\)-esimo predetto risposta lineare (che è altrimenti \(x_i^\top\omega\)).
Quando si stima \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) stiamo essenzialmente stimare la quantità di rumore un gruppo effetto casuale porta che altrimenti attutire il segnale presente in \(x_i^\top\omega\).
Ci sono una varietà di opzioni per il \(\text{Distribution}\) e funzione di collegamento inverso , \(g^{-1}\). Le scelte comuni sono:
- \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
- \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), e,
- \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).
Per maggiori possibilità, vedere il tfp.glm modulo.
Inferenza variazionale
Purtroppo, trovare le stime di massima verosimiglianza dei parametri \(\beta,\{\Sigma_r\}_r^R\) comporta un integrale non analitica. Per aggirare questo problema, invece
- Definire una famiglia parametrizzato di distribuzioni (la "densità surrogato"), indicata \(q_{\lambda}\) in appendice.
- Trova parametri \(\lambda\) modo che \(q_{\lambda}\) è vicino alla nostra vera denstiy bersaglio.
La famiglia di distribuzioni saranno gaussiane indipendenti delle dimensioni appropriate, e da "vicino alla nostra densità target", intenderemo "minimizzando la divergenza Kullback-Leibler ". Si veda ad esempio la sezione 2.2 di "Variational Inference: A Review per gli statistici" per una derivazione ben scritto e la motivazione. In particolare, mostra che minimizzare la divergenza KL equivale a minimizzare il limite inferiore dell'evidenza negativa (ELBO).
Problema del giocattolo
Gelman et al. (2007) "set di dati di radon" è un set di dati a volte utilizzato per dimostrare approcci per la regressione. (Ad esempio, questo strettamente legato messaggio PyMC3 blog .) L'insieme di dati contiene radon misure in ambiente interno di Radon scattate in tutti gli Stati Uniti. Radon è naturalmente ocurring gas radioattivo che è tossico in alte concentrazioni.
Per la nostra dimostrazione, supponiamo di essere interessati a convalidare l'ipotesi che i livelli di Radon siano più alti nelle famiglie che contengono un seminterrato. Sospettiamo anche che la concentrazione di Radon sia correlata al tipo di suolo, cioè a questioni geografiche.
Per inquadrare questo come un problema di machine learning, proveremo a prevedere i livelli di log-radon in base a una funzione lineare del piano su cui è stata effettuata la lettura. Useremo anche la contea come un effetto casuale e così facendo terremo conto delle variazioni dovute alla geografia. In altre parole, useremo un modello misto-effetto lineare generalizzata .
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import os
from six.moves import urllib
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Faremo anche un rapido controllo della disponibilità di una GPU:
if tf.test.gpu_device_name() != '/device:GPU:0':
print("We'll just use the CPU for this run.")
else:
print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))
We'll just use the CPU for this run.
Ottieni set di dati:
Carichiamo il set di dati dai set di dati TensorFlow ed eseguiamo una leggera preelaborazione.
def load_and_preprocess_radon_dataset(state='MN'):
"""Load the Radon dataset from TensorFlow Datasets and preprocess it.
Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
to Minnesota data and preprocess to obtain the following features:
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
df['county_code'] = df.county.cat.codes
# Radon levels are all positive, but log levels are unconstrained
df['log_radon'] = df['radon'].apply(np.log)
# Drop columns we won't use and tidy the index
columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
df = df[columns_to_keep].reset_index(drop=True)
return df
df = load_and_preprocess_radon_dataset()
df.head()
Specializzazione della famiglia GLMM
In questa sezione, specializziamo la famiglia GLMM al compito di prevedere i livelli di radon. Per fare ciò, consideriamo prima il caso speciale a effetto fisso di un GLMM:
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]
Questo modello postula che il radon registro nell'osservazione \(j\) è (in aspettativa) disciplinate dal piano della \(j\)esimo lettura viene fatta in, più una costante di intercettazione. In pseudocodice, potremmo scrivere
def estimate_log_radon(floor):
return intercept + floor_effect[floor]
c'è un peso imparato per ogni piano e un universale intercept termine. Guardando le misurazioni del radon dal piano 0 e 1, sembra che questo potrebbe essere un buon inizio:
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')
df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");
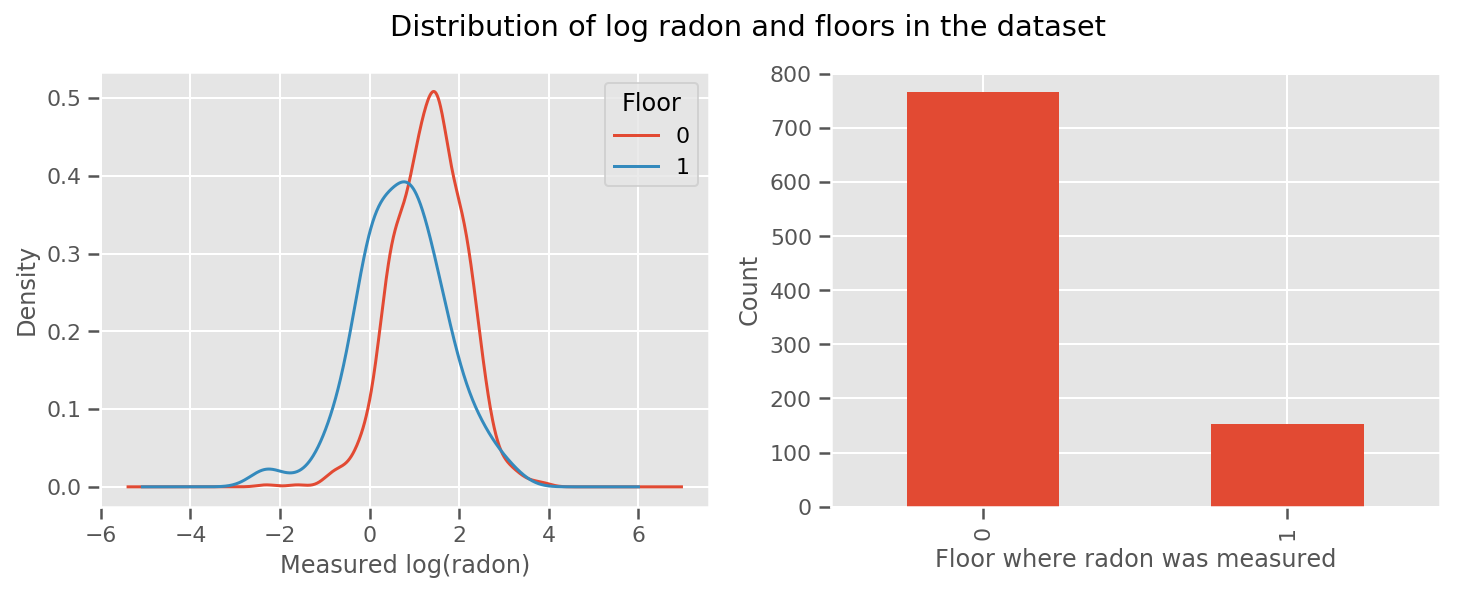
Per rendere il modello un po' più sofisticato, includere qualcosa sulla geografia è probabilmente ancora meglio: il radon fa parte della catena di decadimento dell'uranio, che può essere presente nel terreno, quindi la geografia sembra la chiave per spiegarlo.
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]
Di nuovo, in pseudocodice, abbiamo
def estimate_log_radon(floor, county):
return intercept + floor_effect[floor] + county_effect[county]
lo stesso di prima tranne con un peso specifico della contea.
Dato un set di allenamento sufficientemente ampio, questo è un modello ragionevole. Tuttavia, dati i nostri dati dal Minnesota, vediamo che c'è un gran numero di contee con un piccolo numero di misurazioni. Ad esempio, 39 su 85 contee hanno meno di cinque osservazioni.
Ciò motiva la condivisione della forza statistica tra tutte le nostre osservazioni, in un modo che converge al modello di cui sopra all'aumentare del numero di osservazioni per contea.
fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');
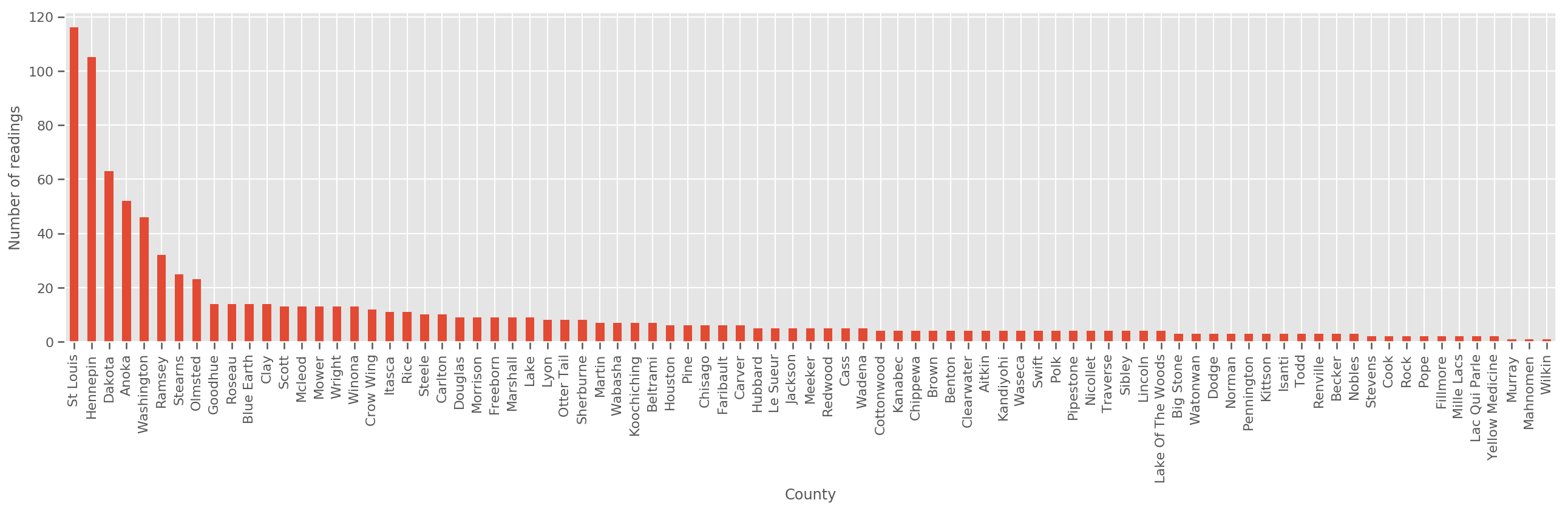
Se noi andiamo bene questo modello, il county_effect vettore sarebbe probabilmente finiscono per memorizzare i risultati per le contee che avevano solo pochi campioni di addestramento, forse overfitting e che porta a poveri generalizzazione.
I GLMM offrono una felice via di mezzo ai due GLM precedenti. Potremmo prendere in considerazione l'adattamento
\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]
Questo modello è lo stesso come il primo, ma abbiamo posto la nostra probabilità di essere una distribuzione normale, e condividerà la varianza attraverso tutte le contee attraverso la (singola) variabile county_scale . In pseudocodice,
def estimate_log_radon(floor, county):
county_mean = county_effect[county]
random_effect = np.random.normal() * county_scale + county_mean
return intercept + floor_effect[floor] + random_effect
Noi inferire la distribuzione congiunta su county_scale , county_mean , e il random_effect utilizzando i nostri dati osservati. Il globale county_scale ci permette di condividere la forza statistica tra province: quelli con molte osservazioni di fornire un colpo alla varianza di contee con poche osservazioni. Inoltre, man mano che raccogliamo più dati, questo modello convergerà al modello senza una variabile di scala aggregata - anche con questo set di dati, arriveremo a conclusioni simili sulle contee più osservate con entrambi i modelli.
Sperimentare
Ora proveremo ad adattare il GLMM di cui sopra utilizzando l'inferenza variazionale in TensorFlow. Per prima cosa suddivideremo i dati in caratteristiche ed etichette.
features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()
Specifica il modello
def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):
def model():
county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
scale=county_scale,
name='county_prior')
random_effect = tf.gather(county_prior, county, axis=-1)
fixed_effect = intercept + floor_weight * floor
linear_response = fixed_effect + random_effect
yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
return tfd.JointDistributionCoroutineAutoBatched(model)
joint = make_joint_distribution_coroutine(
features.floor.values, features.county_code.values, df.county.nunique(),
df.floor.nunique())
# Define a closure over the joint distribution
# to condition on the observed labels.
def target_log_prob_fn(*args):
return joint.log_prob(*args, likelihood=labels)
Specificare surrogato posteriore
Ora messo insieme una famiglia surrogata \(q_{\lambda}\), dove i parametri \(\lambda\) sono addestrabile. In questo caso, la nostra famiglia è distribuzioni indipendenti multivariate normali, uno per ogni parametro, e \(\lambda = \{(\mu_j, \sigma_j)\}\), dove \(j\) indicizza i quattro parametri.
Il metodo che usiamo per adattarsi ai surrogati famiglia usa tf.Variables . Usiamo anche tfp.util.TransformedVariable insieme Softplus per vincolare i parametri (addestrabile) scala per essere positivo. Inoltre, applichiamo Softplus all'intera scale_prior , che è un parametro positivo.
Inizialiamo queste variabili addestrabili con un po' di jitter per aiutare nell'ottimizzazione.
# Initialize locations and scales randomly with `tf.Variable`s and
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
bijector=tfb.Softplus())
n_counties = df.county.nunique()
surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())), # scale_prior
tfd.Normal(_init_loc(), _init_scale()), # intercept
tfd.Normal(_init_loc(), _init_scale()), # floor_weight
tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))]) # county_prior
Si noti che questa cella può essere sostituito con tfp.experimental.vi.build_factored_surrogate_posterior , come in:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=joint.event_shape_tensor()[:-1],
constraining_bijectors=[tfb.Softplus(), None, None, None])
Risultati
Ricordiamo che il nostro obiettivo è definire una famiglia di distribuzioni parametrizzate trattabili, quindi selezionare i parametri in modo da avere una distribuzione trattabile vicina alla nostra distribuzione target.
Abbiamo costruito la distribuzione surrogato sopra, e può utilizzare tfp.vi.fit_surrogate_posterior , che accetta un ottimizzatore e un certo numero di passi per trovare i parametri del modello surrogato minimizzando l'ELBO negativo (che corrisponde nella per minimizzare la divergenza Kullback-Liebler tra il surrogato e la distribuzione target).
Il valore di ritorno è l'ELBO negativo ad ogni passo, e le distribuzioni nel surrogate_posterior sarà stato aggiornato con i parametri trovati dalla ottimizzatore.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior,
optimizer=optimizer,
num_steps=3000,
seed=42,
sample_size=2)
(scale_prior_,
intercept_,
floor_weight_,
county_weights_), _ = surrogate_posterior.sample_distributions()
print(' intercept (mean): ', intercept_.mean())
print(' floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))
intercept (mean): tf.Tensor(1.4352839, shape=(), dtype=float32)
floor_weight (mean): tf.Tensor(-0.6701997, shape=(), dtype=float32)
scale_prior (approx. mean): tf.Tensor(0.28682157, shape=(), dtype=float32)
fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
ylabel="Loss (ELBO)",
title="Loss during training",
ylim=0);
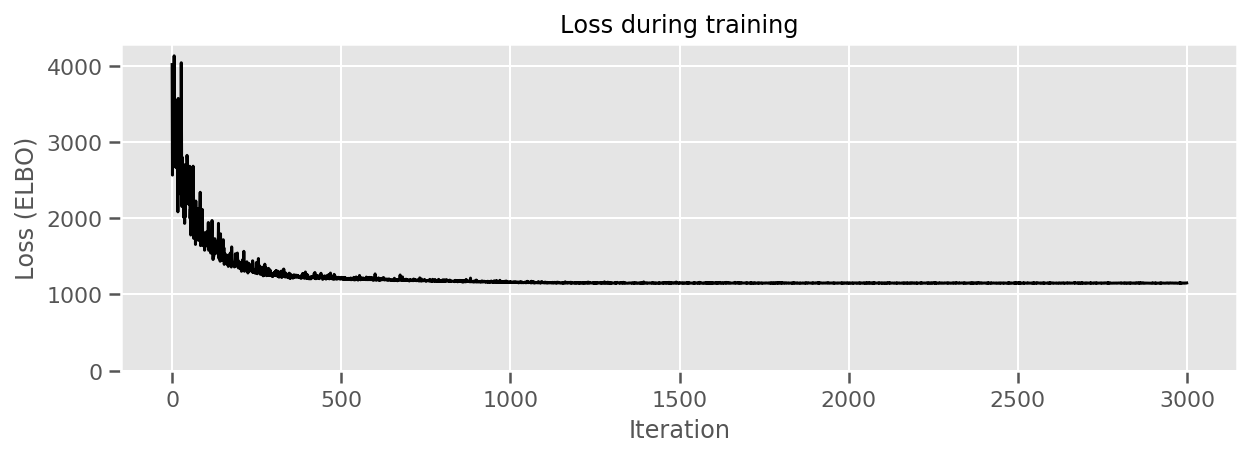
Possiamo tracciare gli effetti medi stimati della contea, insieme all'incertezza di tale media. Abbiamo ordinato questo per numero di osservazioni, con la più grande a sinistra. Notare che l'incertezza è piccola per le contee con molte osservazioni, ma è maggiore per le contee che hanno solo una o due osservazioni.
county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
.agg('size')
.sort_values(ascending=False)
.reset_index(name='count'))
means = county_weights_.mean()
stds = county_weights_.stddev()
fig, ax = plt.subplots(figsize=(20, 5))
for idx, row in county_counts.iterrows():
mid = means[row.county_code]
std = stds[row.county_code]
ax.vlines(idx, mid - std, mid + std, linewidth=3)
ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)
ax.set(
xticks=np.arange(len(county_counts)),
xlim=(-1, len(county_counts)),
ylabel="County effect",
title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);
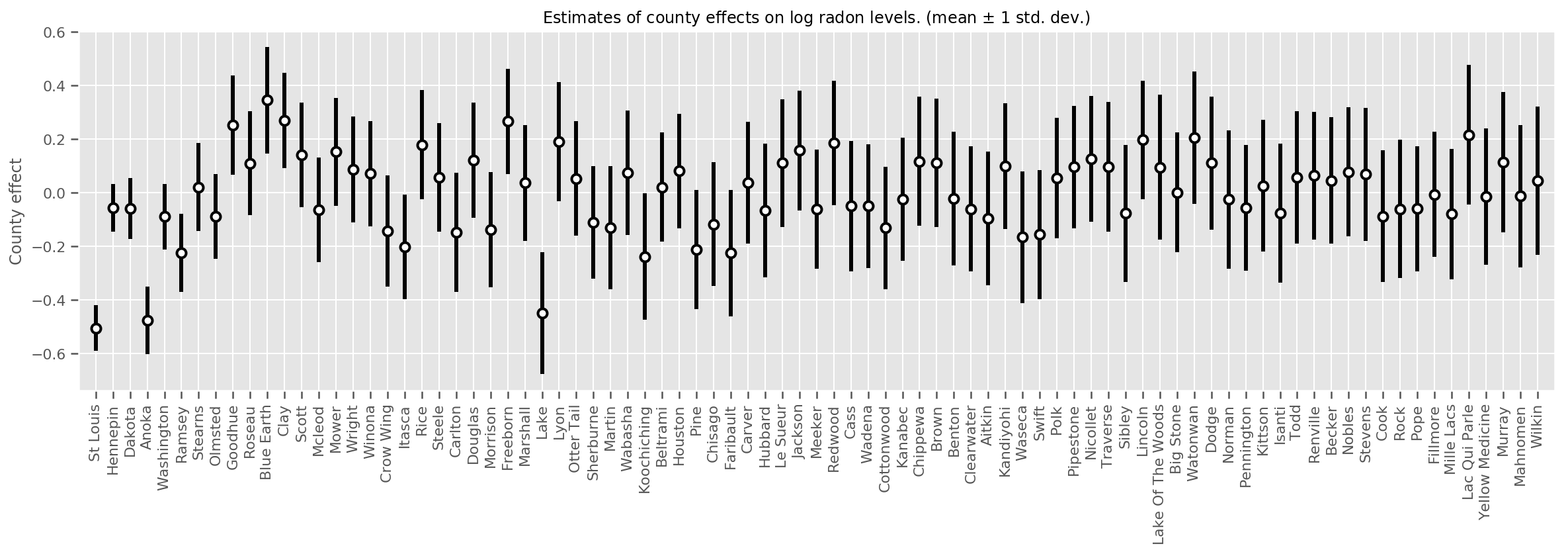
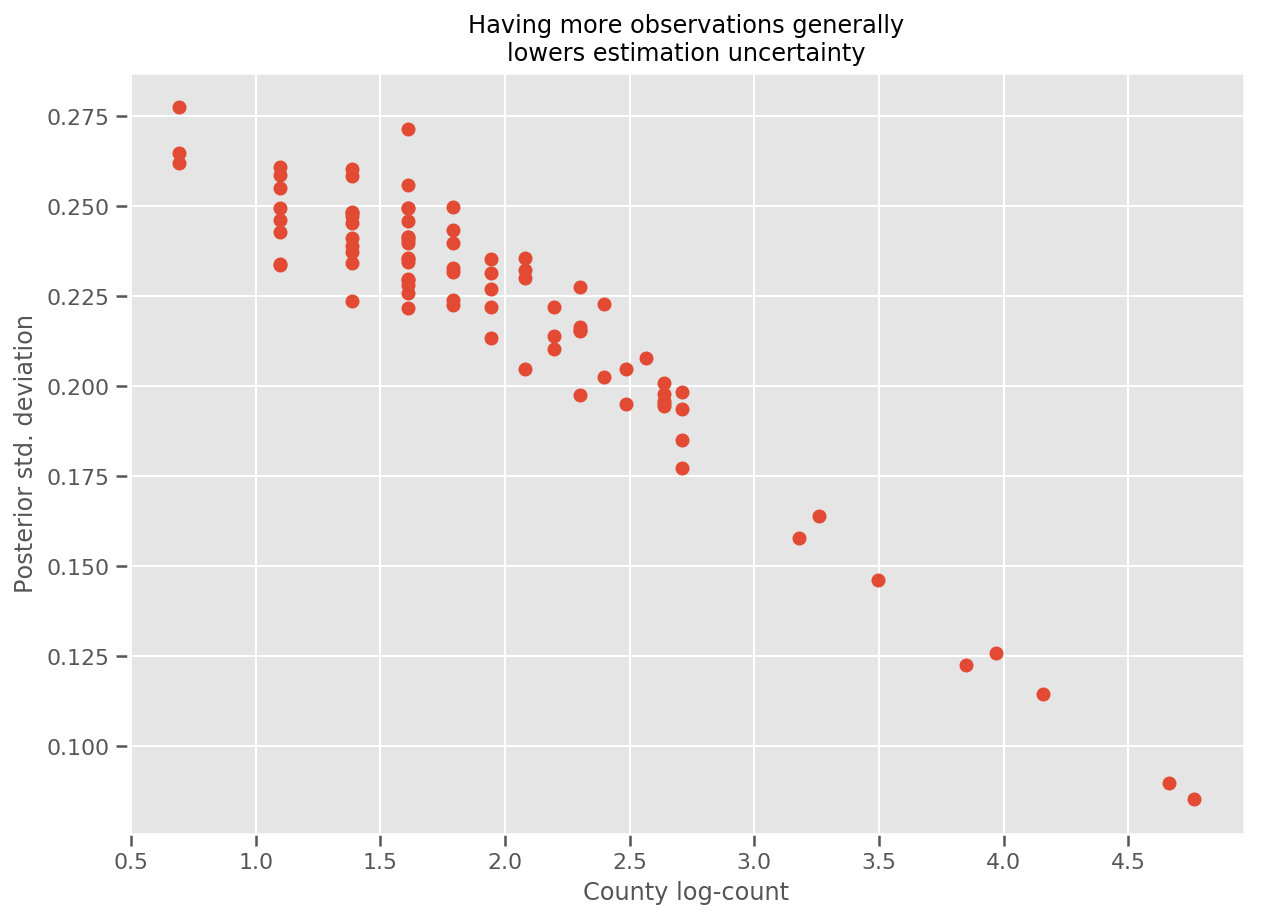
In effetti, possiamo vederlo più direttamente tracciando il log-numero di osservazioni contro la deviazione standard stimata e vedere che la relazione è approssimativamente lineare.
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
ylabel='Posterior std. deviation',
xlabel='County log-count',
title='Having more observations generally\nlowers estimation uncertainty'
);
Confrontando lme4 in R
%%shell
exit # Trick to make this block not execute.
radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)
# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit
# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
# Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
# Groups Name Std.Dev.
# county (Intercept) 0.3282
# Residual 0.7556
# Number of obs: 919, groups: county, 85
# Fixed Effects:
# (Intercept) floor
# 1.462 -0.693
<IPython.core.display.Javascript at 0x7f90b888e9b0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90bce1dfd0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780>
La tabella seguente riassume i risultati.
print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
index=['lme4', 'vi']))
intercept floor scale lme4 1.462000 -0.6930 0.328200 vi 1.435284 -0.6702 0.287251
Questa tabella indica i risultati sono VI all'interno di ~ 10% del lme4 's. Questo è in qualche modo sorprendente poiché:
-
lme4si basa sul metodo di Laplace (non VI), - nessuno sforzo è stato fatto in questa collaborazione per convergere effettivamente,
- è stato fatto uno sforzo minimo per mettere a punto gli iperparametri,
- non è stato fatto alcuno sforzo per regolarizzare o pre-elaborare i dati (ad esempio, caratteristiche del centro, ecc.).
Conclusione
In questa collaborazione abbiamo descritto i modelli a effetti misti lineari generalizzati e mostrato come utilizzare l'inferenza variazionale per adattarli utilizzando TensorFlow Probability. Sebbene il problema del giocattolo avesse solo poche centinaia di campioni di addestramento, le tecniche utilizzate qui sono identiche a quelle necessarie su larga scala.
