Varyasyon Çıkarımını Kullanarak Genelleştirilmiş Doğrusal Karışık Etki Modellerini Uydurma

TensorFlow.org'da görüntüleyin Google Colab'da çalıştırın Kaynağı GitHub'da görüntüleyin Not defterini indir

Düzenlemek

Düzenlemek

Soyut

Bu ortak çalışmada, TensorFlow Olasılığında varyasyon çıkarımı kullanarak genelleştirilmiş bir doğrusal karışık efekt modelinin nasıl uydurulacağını gösteriyoruz.

Model Ailesi

Karma etki modelleri doğrusal Genelleştirilmiş (glmM) benzer modelleri doğrusal genelleştirilmiş da tahmin edilen doğrusal bir yanıt bir örnek, belirli bir gürültü dahil dışında (GLM). Bu, kısmen, nadiren görülen özelliklerin daha sık görülen özelliklerle bilgi paylaşmasına izin verdiği için yararlıdır.

Üretken bir süreç olarak, Genelleştirilmiş Doğrusal Karışık Etkiler Modeli (GLMM) şu şekilde karakterize edilir:

\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]

nerede:

\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]

Diğer bir deyişle, bu, her grubun her kategori örnek, ilişkili olduğunu söyler \(\beta_{rc}\)Çok değişkenli normal. Her ne kadar \(\beta_{rc}\) daima bağımsız çizer, sadece indentically bir grup için dağıtılan \(r\): haber tam bir tane \(\Sigma_r\) her \(r\in\{1,\ldots,R\}\).

Affinely bir, örneğin, grubun özellikleri (ile birleştirildiğinde\(z_{r,i}\)), sonuç hakkında numuneye özgü gürültü \(i\)(aksi takdirde doğrusal bir tepki tahmin inci \(x_i^\top\omega\)).

Biz tahmin zaman \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) Esasen aksi takdirde sinyal mevcut boğmak rastgele etki grubu taşıyan gürültü miktarını tahmin etmeye \(x_i^\top\omega\).

İçin çeşitli seçenekler vardır \(\text{Distribution}\) ve ters bağlantı fonksiyonu , \(g^{-1}\). Ortak seçenekler şunlardır:

  • \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
  • \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), ve
  • \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).

Daha fazla olasılık için bkz tfp.glm modülü.

Varyasyon çıkarımı

Ne yazık ki, parametrelerin maksimum olabilirlik tahminleri bulma \(\beta,\{\Sigma_r\}_r^R\) ni olmayan analitik integrali. Bu sorunu aşmak için bunun yerine

  1. Bir dağılımların parametreli ailesini ( "vekil yoğunluğu"), ifade tanımlayın \(q_{\lambda}\) ekte.
  2. Parametrelerini bulun \(\lambda\) böylece \(q_{\lambda}\) yakın bizim gerçek hedef denstiy etmektir.

Dağılımların aile, biz "minimize anlamına gelecektir bağımsız uygun boyutlarda Gauss ve "hedef yoğunluğuna yakın" tarafından olacaktır Kullback-Leibler sapma ". Örnek için, bkz : "İstatistikçiler için Bir İnceleme Varyasyon Çıkarım" Bölüm 2.2 iyi yazılmış türev ve motivasyon. Özellikle, KL sapmasını en aza indirmenin, olumsuz kanıt alt sınırını (ELBO) en aza indirmeye eşdeğer olduğunu gösterir.

Oyuncak Problemi

Gelman ve ark. (2007) "radon veri kümesi" bazen regresyon için yaklaşımlar göstermek için kullanılan bir veri kümesi olduğunu. (Örneğin, bu yakından ilişkili PyMC3 blog yazısı .) Radon veri kümesi Birleşik Devletleri boyunca alınan Radon kapalı ölçümlerini içerir. Radon doğal olarak, radyoaktif bir gaz olarak oluşan bir toksik yüksek konsantrasyonlarda.

Gösterimiz için, bodrum içeren evlerde Radon seviyelerinin daha yüksek olduğu hipotezini doğrulamakla ilgilendiğimizi varsayalım. Ayrıca Radon konsantrasyonunun toprak tipiyle, yani coğrafyayla ilgili olduğundan şüpheleniyoruz.

Bunu bir ML problemi olarak çerçevelemek için, okumanın yapıldığı zeminin lineer fonksiyonuna dayalı log-radon seviyelerini tahmin etmeye çalışacağız. Ayrıca ilçeyi rastgele bir etki olarak kullanacağız ve bunu yaparken coğrafyadan kaynaklanan farklılıkları hesaba katacağız. Başka bir deyişle, bir kullanacağız genelleştirilmiş doğrusal karma etki modeli .

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import os
from six.moves import urllib

import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

Ayrıca bir GPU'nun kullanılabilirliği için hızlı bir kontrol yapacağız:

if tf.test.gpu_device_name() != '/device:GPU:0':
  print("We'll just use the CPU for this run.")
else:
  print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))

We'll just use the CPU for this run.

Veri Kümesini Alın:

Veri kümesini TensorFlow veri kümelerinden yükler ve hafif ön işlemler yaparız.

def load_and_preprocess_radon_dataset(state='MN'):
  """Load the Radon dataset from TensorFlow Datasets and preprocess it.

  Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
  to Minnesota data and preprocess to obtain the following features:
  - `county`: Name of county in which the measurement was taken.
  - `floor`: Floor of house (0 for basement, 1 for first floor) on which the
    measurement was taken.

  The target variable is `log_radon`, the log of the Radon measurement in the
  house.
  """
  ds = tfds.load('radon', split='train')
  radon_data = tfds.as_dataframe(ds)
  radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
  df = radon_data[radon_data.state==state.encode()].copy()

  df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
  # Make county names look nice. 
  df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
  # Remap categories to start from 0 and end at max(category).
  df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
  df['county_code'] = df.county.cat.codes
  # Radon levels are all positive, but log levels are unconstrained
  df['log_radon'] = df['radon'].apply(np.log)

  # Drop columns we won't use and tidy the index 
  columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
  df = df[columns_to_keep].reset_index(drop=True)

  return df

df = load_and_preprocess_radon_dataset()
df.head()

GLMM Ailesini Uzmanlaştırmak

Bu bölümde, GLMM ailesini radon seviyelerini tahmin etme görevi için özelleştiriyoruz. Bunu yapmak için önce bir GLMM'nin sabit etkili özel durumunu ele alıyoruz:

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]

Gözlem günlük radon o Bu model mn var olduğunu varsaymaktadır \(j\) katında tarafından yönetilir (beklenti içinde) 'dir \(j\)inci okuma alınır, artı bazı sabit yolunu kesmek. Sözde kodda yazabiliriz

def estimate_log_radon(floor):
    return intercept + floor_effect[floor]

Her katta ve evrensel için öğrenilen bir ağırlık var intercept dönem. 0 ve 1. kattaki radon ölçümlerine bakıldığında, bunun iyi bir başlangıç ​​olabileceği görülüyor:

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')

df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");

png

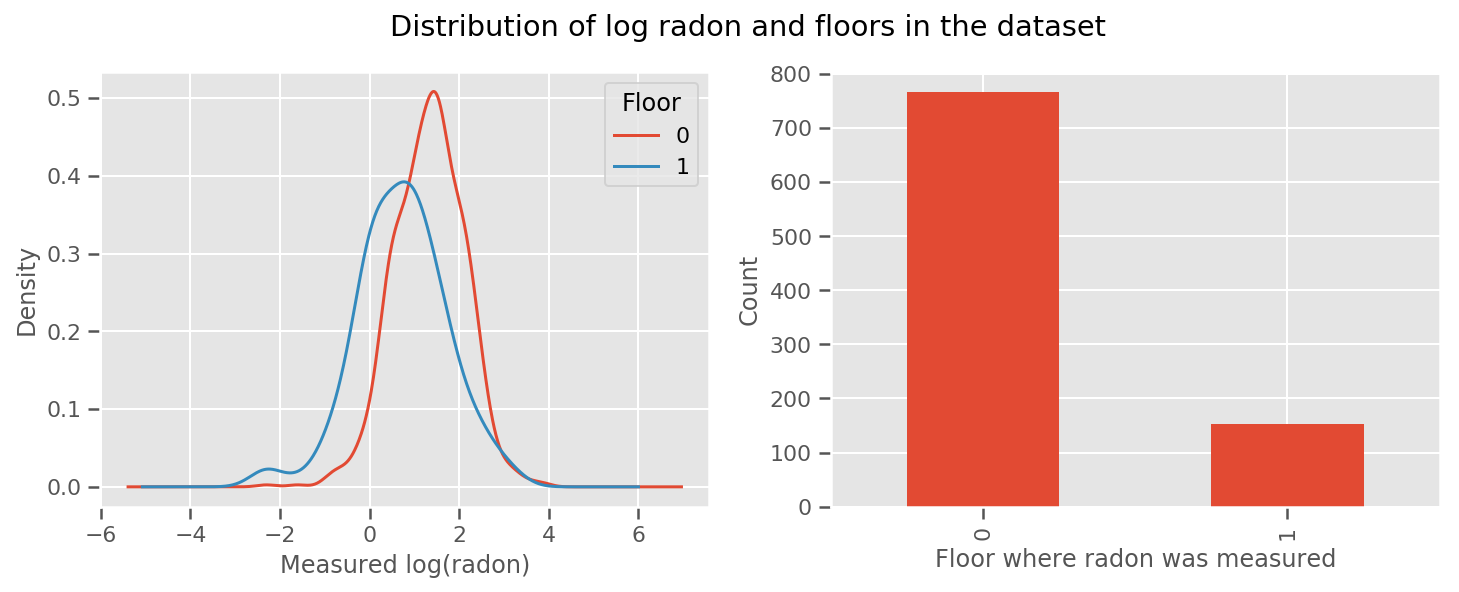
Modeli biraz daha karmaşık hale getirmek, coğrafya hakkında bir şeyler dahil etmek muhtemelen daha da iyidir: radon, toprakta mevcut olabilecek uranyumun bozunma zincirinin bir parçasıdır, bu nedenle coğrafya hesaba katılması gereken bir anahtar gibi görünüyor.

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]

Yine, sözde kodda,

def estimate_log_radon(floor, county):
    return intercept + floor_effect[floor] + county_effect[county]

ilçeye özgü ağırlık dışında öncekiyle aynı.

Yeterince büyük bir eğitim seti verildiğinde, bu makul bir modeldir. Ancak Minnesota'dan aldığımız verilere göre, az sayıda ölçüme sahip çok sayıda ilçe olduğunu görüyoruz. Örneğin, 85 ilçeden 39'unun beşten az gözlemi var.

Bu, ilçe başına gözlem sayısı arttıkça yukarıdaki modele yakınsayan bir şekilde tüm gözlemlerimiz arasında istatistiksel gücün paylaşılmasını motive eder.

fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');

png

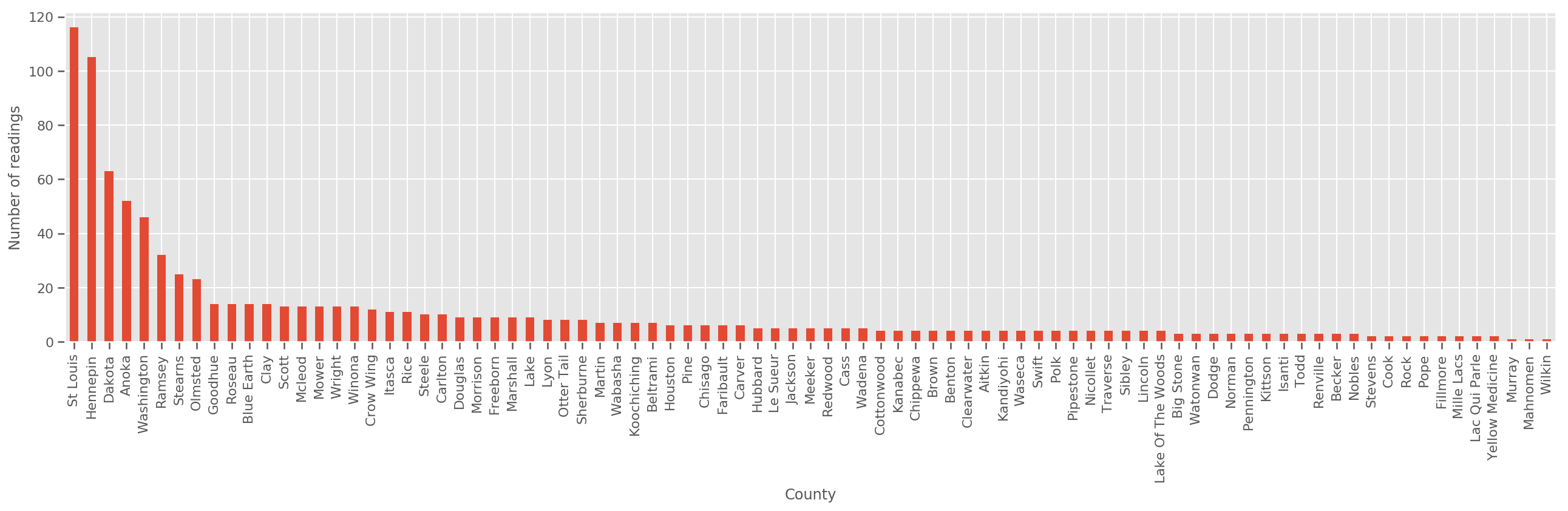
Biz bu modeli uyuyorsanız, county_effect vektör olasılıkla belki overfitting ve yoksul genelleme yol açan sadece birkaç antrenman örnekleri vardı ilçeleri için sonuçları ezberlemek sona ereceğini.

GLMM'ler, yukarıdaki iki GLM'ye mutlu bir orta sunar. uydurmayı düşünebiliriz

\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]

Bu model ilk aynıdır, ama biz bir normal dağılım olmak bizim olasılığını düzeltti ve (tek) değişken aracılığıyla tüm ilçeleri varyansı paylaşacak county_scale . sözde kodda,

def estimate_log_radon(floor, county):
    county_mean = county_effect[county]
    random_effect = np.random.normal() * county_scale + county_mean
    return intercept + floor_effect[floor] + random_effect

Biz üzerinde ortak dağılımını anlaması olacak county_scale , county_mean ve random_effect bizim gözlenen verileri kullanarak. Küresel county_scale birçok gözlemlerle bu birkaç gözlemlerle ilçelerinde uymayacak bir isabet sağlar: bize ilçedeki istatistiksel gücünü paylaşmalarını sağlar. Ayrıca, daha fazla veri topladıkça, bu model havuzlanmış bir ölçek değişkeni olmadan modele yakınsar - bu veri seti ile bile, her iki modelle de en çok gözlemlenen ilçeler hakkında benzer sonuçlara varacağız.

Deney

Şimdi TensorFlow'da varyasyon çıkarımını kullanarak yukarıdaki GLMM'ye uymaya çalışacağız. İlk önce verileri özelliklere ve etiketlere böleceğiz.

features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()

Modeli Belirtin

def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):

  def model():
    county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
    intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
    floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
    county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
                                    scale=county_scale,
                                    name='county_prior')
    random_effect = tf.gather(county_prior, county, axis=-1)

    fixed_effect = intercept + floor_weight * floor
    linear_response = fixed_effect + random_effect
    yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
  return tfd.JointDistributionCoroutineAutoBatched(model)

joint = make_joint_distribution_coroutine(
    features.floor.values, features.county_code.values, df.county.nunique(),
    df.floor.nunique())

# Define a closure over the joint distribution 
# to condition on the observed labels.
def target_log_prob_fn(*args):
  return joint.log_prob(*args, likelihood=labels)

vekil posterior belirtin

Biz şimdi birlikte bir vekil aile koymak \(q_{\lambda}\)parametreleri, \(\lambda\) eğitilebilir bulunmaktadır. Bu durumda, ailemiz bağımsız değişkenli normal dağılım, her parametre için olandır ve \(\lambda = \{(\mu_j, \sigma_j)\}\), \(j\) indeksleri dört parametre.

Yöntem biz vekil aile kullandığı uyacak şekilde kullanmak tf.Variables . Biz de kullanmak tfp.util.TransformedVariable birlikte Softplus pozitif (öğretilebilir) ölçek parametreleri sınırlamak için. Ayrıca, başvuru Softplus tüm için scale_prior olumlu bir parametredir.

Optimizasyona yardımcı olması için bu eğitilebilir değişkenleri biraz titreşimle başlatıyoruz.

# Initialize locations and scales randomly with `tf.Variable`s and 
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
    tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
    initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
    bijector=tfb.Softplus())
n_counties = df.county.nunique()

surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
  tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())),           # scale_prior
  tfd.Normal(_init_loc(), _init_scale()),                           # intercept
  tfd.Normal(_init_loc(), _init_scale()),                           # floor_weight
  tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))])  # county_prior

Not bu hücre ile değiştirilebilir olduğunu tfp.experimental.vi.build_factored_surrogate_posterior olduğu gibi:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
  event_shape=joint.event_shape_tensor()[:-1],
  constraining_bijectors=[tfb.Softplus(), None, None, None])

Sonuçlar

Amacımızın izlenebilir parametreli bir dağılım ailesi tanımlamak olduğunu hatırlayın ve ardından hedef dağılımımıza yakın izlenebilir bir dağılıma sahip olmamız için parametreleri seçin.

Yukarıda vekil dağılımı yerleşik ve kullanabilirsiniz tfp.vi.fit_surrogate_posterior negatif Elbo minimize vekil model parametrelerini (arasında Kullback-Liebler sapma en aza indirmek için corresonds bulmak için optimize edici ve adımların belirli bir sayıda kabul hangi vekil ve hedef dağılım).

Dönüş değeri her adımda negatif ELBO olduğunu ve içinde dağılımları surrogate_posterior parametreleri optimize edici bulduğu güncellendi olacaktır.

optimizer = tf.optimizers.Adam(learning_rate=1e-2)

losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn, 
    surrogate_posterior,
    optimizer=optimizer,
    num_steps=3000, 
    seed=42,
    sample_size=2)

(scale_prior_, 
 intercept_, 
 floor_weight_, 
 county_weights_), _ = surrogate_posterior.sample_distributions()

print('        intercept (mean): ', intercept_.mean())
print('     floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))

intercept (mean):  tf.Tensor(1.4352839, shape=(), dtype=float32)
     floor_weight (mean):  tf.Tensor(-0.6701997, shape=(), dtype=float32)
 scale_prior (approx. mean):  tf.Tensor(0.28682157, shape=(), dtype=float32)

fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
       ylabel="Loss (ELBO)",
       title="Loss during training",
       ylim=0);

png

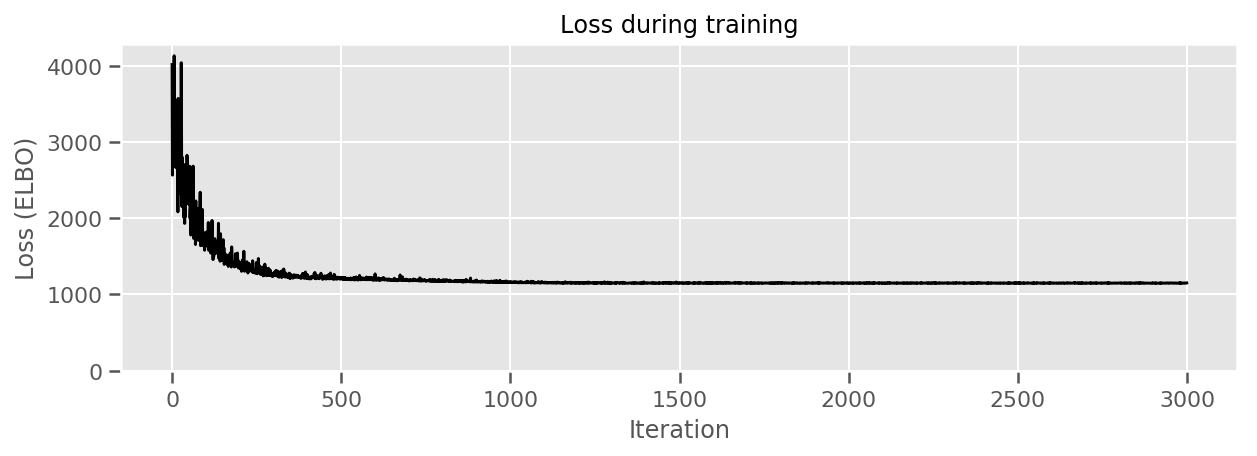
Tahmini ortalama ilçe etkilerini, bu ortalamanın belirsizliği ile birlikte çizebiliriz. Bunu, en büyüğü solda olacak şekilde gözlem sayısına göre sıraladık. Belirsizliğin çok sayıda gözlemi olan ilçeler için küçük olduğuna, ancak yalnızca bir veya iki gözlemi olan ilçeler için daha büyük olduğuna dikkat edin.

county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
                   .agg('size')
                   .sort_values(ascending=False)
                   .reset_index(name='count'))

means = county_weights_.mean()
stds = county_weights_.stddev()

fig, ax = plt.subplots(figsize=(20, 5))

for idx, row in county_counts.iterrows():
  mid = means[row.county_code]
  std = stds[row.county_code]
  ax.vlines(idx, mid - std, mid + std, linewidth=3)
  ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)

ax.set(
    xticks=np.arange(len(county_counts)),
    xlim=(-1, len(county_counts)),
    ylabel="County effect",
    title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);

png

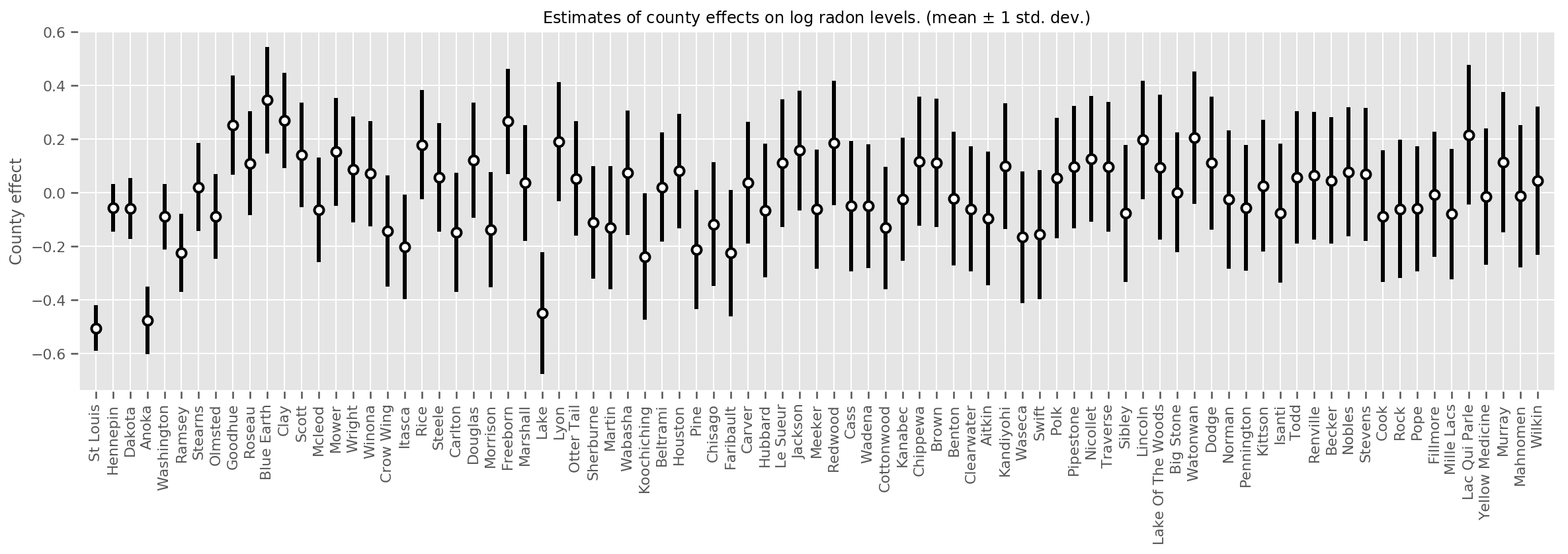
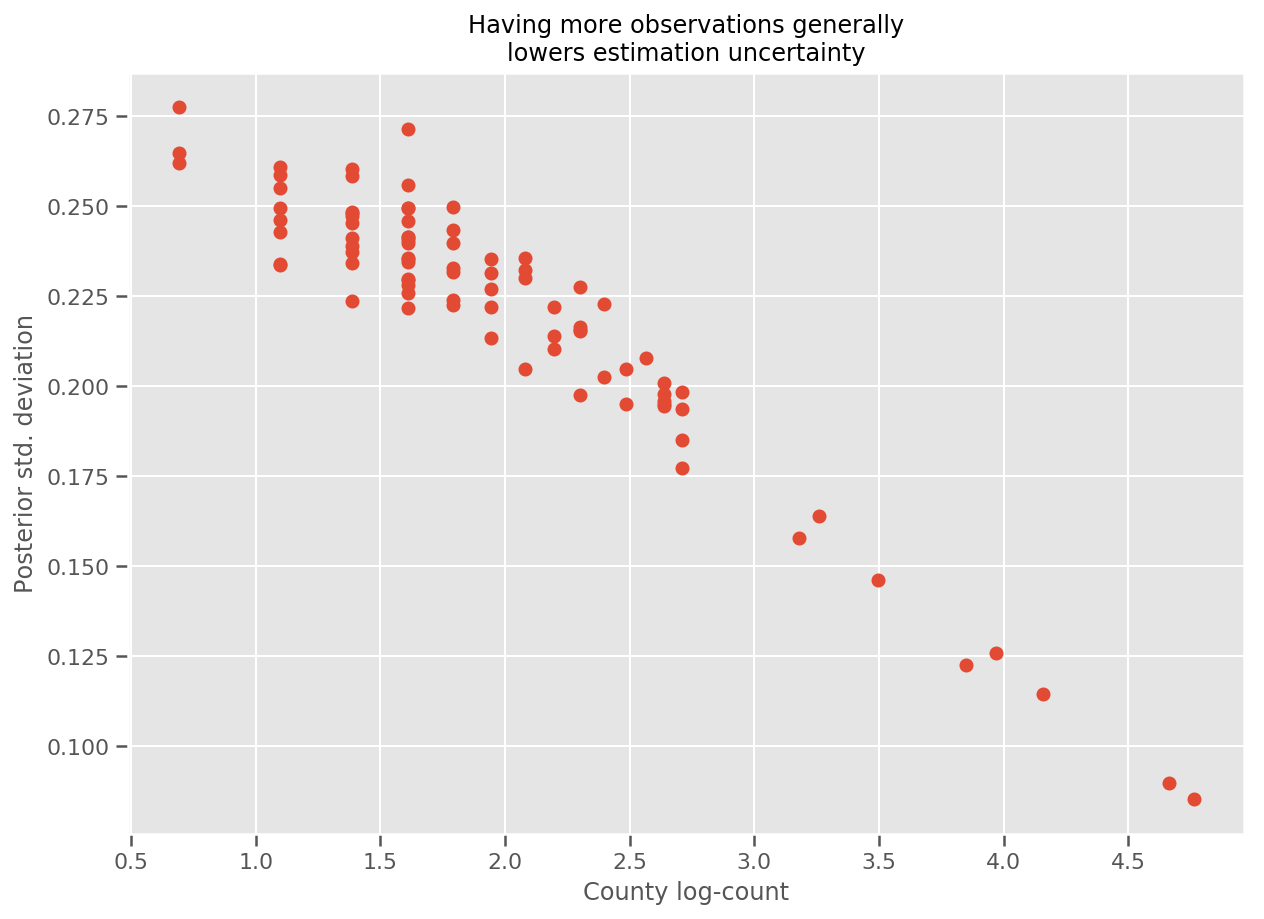
Aslında, bunu daha doğrudan gözlemlerin log sayısını tahmini standart sapmaya karşı çizerek görebiliriz ve ilişkinin yaklaşık olarak doğrusal olduğunu görebiliriz.

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
    ylabel='Posterior std. deviation',
    xlabel='County log-count',
    title='Having more observations generally\nlowers estimation uncertainty'
);

png

Karşılaştırarak lme4 R

%%shell
exit  # Trick to make this block not execute.

radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)

# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit

# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
#    Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
#  Groups   Name        Std.Dev.
#  county   (Intercept) 0.3282
#  Residual             0.7556
# Number of obs: 919, groups:  county, 85
# Fixed Effects:
# (Intercept)        floor
#       1.462       -0.693

<IPython.core.display.Javascript at 0x7f90b888e9b0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90bce1dfd0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>

Aşağıdaki tablo sonuçları özetlemektedir.

print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
                             floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
                             scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
                   index=['lme4', 'vi']))

intercept   floor     scale
lme4   1.462000 -0.6930  0.328200
vi     1.435284 -0.6702  0.287251

Bu tablo, VI sonuç ~ içinde% 10 olduğunu gösterir lme4 Var. Bu biraz şaşırtıcı çünkü:

  • lme4 dayanmaktadır Laplace yöntemi (değil VI)
  • bu birlikte çalışma içinde gerçekten yakınlaşmak için hiçbir çaba gösterilmedi,
  • hiperparametreleri ayarlamak için minimum çaba sarf edildi,
  • verileri düzenlemek veya önceden işlemek için hiçbir çaba gösterilmedi (örneğin, merkez özellikleri, vb.).

Çözüm

Bu ortak çalışmada, Genelleştirilmiş Doğrusal Karışık Etki Modellerini tanımladık ve TensorFlow Olasılığı kullanarak bunlara uyması için varyasyonel çıkarımın nasıl kullanılacağını gösterdik. Oyuncak problemi sadece birkaç yüz eğitim örneğine sahip olsa da, burada kullanılan teknikler ölçekte ihtiyaç duyulanlarla aynıdır.