 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
Un modello lineare a effetti misti è un approccio semplice per modellare relazioni lineari strutturate (Harville, 1997; Laird e Ware, 1982). Ogni punto dati è costituito da input di vario tipo, classificati in gruppi, e un output a valori reali. Un modello a effetti misti lineare è un modello gerarchico: condivide la forza statistica tra i gruppi, al fine di migliorare le inferenze su qualsiasi punto dati individuali.
In questo tutorial, dimostriamo modelli lineari di effetti misti con un esempio reale in TensorFlow Probability. Useremo la catena JointDistributionCoroutine e Markov Monte Carlo ( tfp.mcmc ) moduli.
Dipendenze e prerequisiti
Importa e configura
import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')
Fai le cose velocemente!
Prima di immergerci, assicuriamoci di utilizzare una GPU per questa demo.
Per fare ciò, seleziona "Runtime" -> "Cambia tipo di runtime" -> "Acceleratore hardware" -> "GPU".
Il seguente frammento verificherà che abbiamo accesso a una GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
Dati
Usiamo i InstEval set di dati dalla famosa lme4 pacchetto R (Bates et al., 2015). È un insieme di dati di corsi e le loro valutazioni di valutazione. Ogni corso comprende metadati quali students , instructors e departments , e la variabile risposta di interesse è il punteggio di valutazione.
def load_insteval():
"""Loads the InstEval data set.
It contains 73,421 university lecture evaluations by students at ETH
Zurich with a total of 2,972 students, 2,160 professors and
lecturers, and several student, lecture, and lecturer attributes.
Implementation is built from the `observations` Python package.
Returns:
Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
dictionary `metadata` of column headers (feature names).
"""
url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
'lme4/InstEval.csv')
with requests.Session() as s:
download = s.get(url)
f = download.content.decode().splitlines()
iterator = csv.reader(f)
columns = next(iterator)[1:]
x_train = np.array([row[1:] for row in iterator], dtype=np.int)
metadata = {'columns': columns}
return x_train, metadata
Carichiamo e preprocessiamo il set di dati. Conserviamo il 20% dei dati in modo da poter valutare il nostro modello adattato su punti dati invisibili. Di seguito visualizziamo le prime righe.
data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
'd': 'instructors',
'dept': 'departments',
'y': 'ratings'})
data['students'] -= 1 # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes
train = data.sample(frac=0.8)
test = data.drop(train.index)
train.head()
Abbiamo istituito il set di dati in termini di una features Dizionario di input e un labels uscita corrispondente alle valutazioni. Ogni caratteristica è codificata come un numero intero e ogni etichetta (valutazione) è codificata come un numero a virgola mobile.
get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
k: get_value(train, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)
features_test = {k: get_value(test, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)
num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]
print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)
Number of students: 2972 Number of instructors: 1128 Number of departments: 14 Number of observations: 58737
Modello
Un tipico modello lineare presuppone l'indipendenza, in cui ogni coppia di punti dati ha una relazione lineare costante. Nella InstEval set di dati, osservazioni nascono in gruppi ciascuno dei quali può avere diverse piste e intercetta. I modelli lineari a effetti misti, noti anche come modelli lineari gerarchici o modelli lineari multilivello, catturano questo fenomeno (Gelman & Hill, 2006).
Esempi di questo fenomeno includono:
- Studenti. Le osservazioni di uno studente non sono indipendenti: alcuni studenti possono dare sistematicamente valutazioni basse (o alte) delle lezioni.
- Istruttori. Le osservazioni di un istruttore non sono indipendenti: ci aspettiamo che i buoni insegnanti abbiano generalmente buone valutazioni e che i cattivi insegnanti abbiano generalmente cattive valutazioni.
- Dipartimenti. Le osservazioni di un dipartimento non sono indipendenti: alcuni dipartimenti possono generalmente avere materiale secco o una classificazione più rigorosa e quindi essere valutati più bassi di altri.
Per catturare questo, ricordare che per un set di dati di \(N\times D\) dispone \(\mathbf{X}\) e \(N\) etichette \(\mathbf{y}\), postulati di regressione lineare del modello
\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]
dove c'è un pendio vettore \(\beta\in\mathbb{R}^D\), intercetta \(\alpha\in\mathbb{R}\)e rumore casuale \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Diciamo che \(\beta\) e \(\alpha\) sono "effetti fissi": sono gli effetti mantenendo costanti in tutta la popolazione di punti dati \((x, y)\). Una formulazione equivalente dell'equazione come probabilità è \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\). Questa probabilità è massimizzata durante l'inferenza al fine di trovare stime puntuali di \(\beta\) e \(\alpha\) che si adattano i dati.
Un modello lineare a effetti misti estende la regressione lineare come
\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]
dove c'è ancora una pendenza vettore \(\beta\in\mathbb{R}^P\), intercetta \(\alpha\in\mathbb{R}\)e rumore casuale \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Inoltre, v'è un termine \(\mathbf{Z}\eta\), dove \(\mathbf{Z}\) è una matrice caratteristiche e \(\eta\in\mathbb{R}^Q\) è un vettore di piste casuali; \(\eta\) distribuzione normale con parametro di un componente varianza \(\sigma^2\). \(\mathbf{Z}\) è formato da partizionamento originale \(N\times D\) caratteristiche matrice in termini di una nuova \(N\times P\) matrice \(\mathbf{X}\) e \(N\times Q\) matrice \(\mathbf{Z}\), dove \(P + Q=D\): questa partizione permette di modellare le caratteristiche separatamente utilizzando l'effetti fissi \(\beta\) e la variabile latente \(\eta\) rispettivamente.
Diciamo le variabili latenti \(\eta\) sono "effetti casuali": sono gli effetti che variano in tutta la popolazione (anche se possono essere costante in sottopopolazioni). In particolare, poiché gli effetti casuali \(\eta\) hanno media 0, medio dell'etichetta dati viene catturato da \(\mathbf{X}\beta + \alpha\). Gli effetti casuali componente \(\mathbf{Z}\eta\) variazioni Cattura nei dati: "Istruttore # 54 è valutato 1,4 punti in più rispetto alla media", per esempio,
In questo tutorial, poniamo i seguenti effetti:
- Effetti fissi:
service.serviceè una covariata binario a seconda che il corso appartiene al reparto principale dell'istruttore. Non importa quanto i dati aggiuntivi raccolti, si può assumere solo valori \(0\) e \(1\). - Gli effetti casuali:
students,instructorsedepartments. Date più osservazioni dalla popolazione delle valutazioni di valutazione del corso, potremmo guardare a nuovi studenti, insegnanti o dipartimenti.
Nella sintassi del pacchetto lme4 di R (Bates et al., 2015), il modello può essere riassunto come
ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1
dove x indica un effetto fisso (1|x) denota un effetto casuale per x , e 1 indica un termine di intercetta.
Implementiamo questo modello di seguito come JointDistribution. Per avere un migliore supporto per il monitoraggio dei parametri (ad esempio, vogliamo seguire tutto il tf.Variable in model.trainable_variables ), abbiamo implementare il modello di modello come tf.Module .
class LinearMixedEffectModel(tf.Module):
def __init__(self):
# Set up fixed effects and other parameters.
# These are free parameters to be optimized in E-steps
self._intercept = tf.Variable(0., name="intercept") # alpha in eq
self._effect_service = tf.Variable(0., name="effect_service") # beta in eq
self._stddev_students = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_students") # sigma in eq
self._stddev_instructors = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_instructors") # sigma in eq
self._stddev_departments = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_departments") # sigma in eq
def __call__(self, features):
model = tfd.JointDistributionSequential([
# Set up random effects.
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_students),
scale_identity_multiplier=self._stddev_students),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_instructors),
scale_identity_multiplier=self._stddev_instructors),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_departments),
scale_identity_multiplier=self._stddev_departments),
# This is the likelihood for the observed.
lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
tfd.Normal(
loc=(self._effect_service * features["service"] +
tf.gather(effect_students, features["students"], axis=-1) +
tf.gather(effect_instructors, features["instructors"], axis=-1) +
tf.gather(effect_departments, features["departments"], axis=-1) +
self._intercept),
scale=1.),
reinterpreted_batch_ndims=1)
])
# To enable tracking of the trainable variables via the created distribution,
# we attach a reference to `self`. Since all TFP objects sub-class
# `tf.Module`, this means that the following is possible:
# LinearMixedEffectModel()(features_train).trainable_variables
# ==> tuple of all tf.Variables created by LinearMixedEffectModel.
model._to_track = self
return model
lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)
lmm_train.trainable_variables
(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)
Come programma grafico probabilistico, possiamo anche visualizzare la struttura del modello in termini del suo grafico computazionale. Questo grafico codifica il flusso di dati attraverso le variabili casuali nel programma, rendendo esplicite le loro relazioni in termini di un modello grafico (Jordan, 2003).
Come strumento statistica, potremmo esaminiamo il grafico per meglio vedere, per esempio, che intercept e effect_service sono condizionalmente trovati dipendenti ratings ; questo potrebbe essere più difficile da vedere dal codice sorgente se il programma è scritto con classi, riferimenti incrociati tra moduli e/o subroutine. Come strumento di calcolo, potremmo anche notare variabili latenti sfociano nel ratings variabile tramite tf.gather ops. Questo può essere un collo di bottiglia su determinati acceleratori hardware se indicizzazione Tensor s è costoso; la visualizzazione del grafico lo rende immediatamente evidente.
lmm_train.resolve_graph()
(('effect_students', ()),
('effect_instructors', ()),
('effect_departments', ()),
('x', ('effect_departments', 'effect_instructors', 'effect_students')))
Stima dei parametri
Dato i dati, l'obiettivo di inferenza è quello di adattare il modello di pista effetti fissi \(\beta\), intercetta \(\alpha\), e varianza parametro di un componente \(\sigma^2\). Il principio di massima verosimiglianza formalizza questo compito come
\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]
In questo tutorial, usiamo l'algoritmo EM Monte Carlo per massimizzare questa densità marginale (Dempster et al., 1977; Wei e Tanner, 1990).¹ Eseguiamo la catena di Markov Monte Carlo per calcolare l'aspettativa della verosimiglianza condizionata rispetto al effetti casuali ("E-step"), ed eseguiamo la discesa del gradiente per massimizzare l'aspettativa rispetto ai parametri ("M-step"):
Per l'E-step, abbiamo impostato Hamiltonian Monte Carlo (HMC). Prende uno stato corrente (gli effetti dello studente, dell'insegnante e del dipartimento) e restituisce un nuovo stato. Assegniamo il nuovo stato alle variabili TensorFlow, che indicheranno lo stato della catena HMC.
Per il passo M, usiamo il campione posteriore da HMC per calcolare una stima imparziale della verosimiglianza marginale fino a una costante. Applichiamo quindi il suo gradiente rispetto ai parametri di interesse. Questo produce un passo di discesa stocastico imparziale sulla verosimiglianza marginale. Lo implementiamo con l'ottimizzatore Adam TensorFlow e riduciamo al minimo il negativo del marginale.
target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]
# For debugging
target_log_prob_fn(*current_state)
<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>
# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.015,
num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)
@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
next_state, next_kernel_results = hmc.one_step(
current_state=current_state,
previous_kernel_results=kernel_results)
return next_state, next_kernel_results
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
with tf.GradientTape() as tape:
loss = -target_log_prob_fn(*current_state)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
Eseguiamo una fase di riscaldamento, che esegue una catena MCMC per un numero di iterazioni in modo che l'allenamento possa essere inizializzato all'interno della massa di probabilità del posteriore. Quindi eseguiamo un ciclo di allenamento. Esegue congiuntamente i passaggi E e M e registra i valori durante l'allenamento.
num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])
# Run warm-up stage.
for t in range(num_warmup_iters):
current_state, kernel_results = one_e_step(current_state, kernel_results)
num_accepted += kernel_results.is_accepted.numpy()
if t % 500 == 0 or t == num_warmup_iters - 1:
print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
t, num_accepted / (t + 1)))
num_accepted = 0 # reset acceptance rate counter
# Run training.
for t in range(num_iters):
# run 5 MCMC iterations before every joint EM update
for _ in range(5):
current_state, kernel_results = one_e_step(current_state, kernel_results)
loss = one_m_step(current_state)
effect_students_samples[t, :] = current_state[0].numpy()
effect_instructors_samples[t, :] = current_state[1].numpy()
effect_departments_samples[t, :] = current_state[2].numpy()
num_accepted += kernel_results.is_accepted.numpy()
loss_history[t] = loss.numpy()
if t % 500 == 0 or t == num_iters - 1:
print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
t, num_accepted / (t + 1), loss_history[t]))
Warm-Up Iteration: 0 Acceptance Rate: 1.000 Warm-Up Iteration: 500 Acceptance Rate: 0.754 Warm-Up Iteration: 999 Acceptance Rate: 0.707 Iteration: 0 Acceptance Rate: 1.000 Loss: 98220.266 Iteration: 500 Acceptance Rate: 0.703 Loss: 96003.969 Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609 Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891
Si può anche scrivere il riscaldamento per-loop in una tf.while_loop , e il passo di formazione in un tf.scan o tf.while_loop per ancora più veloce l'inferenza. Per esempio:
@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
_, next_state, next_kernel_results = tf.while_loop(
cond=lambda i, state, pkr: i < k,
body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
loop_vars=(tf.constant(0), current_state, kernel_results)
)
return next_state, next_kernel_results
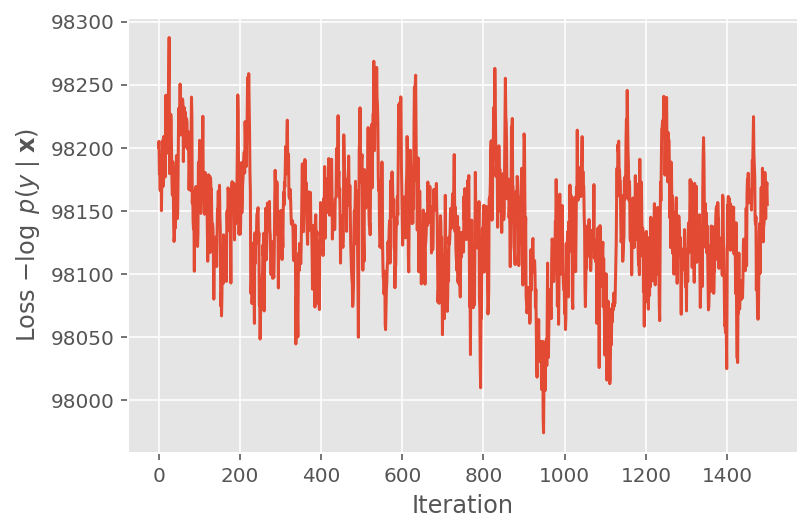
Sopra, non abbiamo eseguito l'algoritmo fino a quando non è stata rilevata una soglia di convergenza. Per verificare se l'addestramento fosse sensato, verifichiamo che la funzione di perdita tende effettivamente a convergere sulle iterazioni di addestramento.
plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()
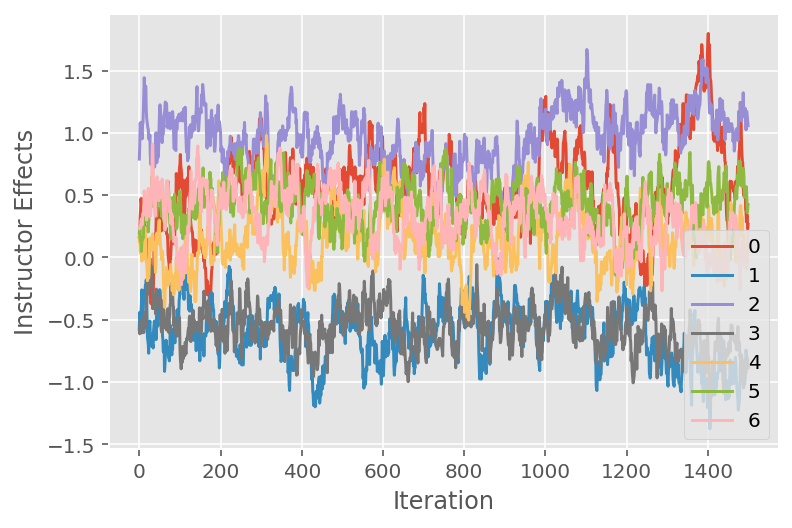
Usiamo anche un tracciato, che mostra la traiettoria dell'algoritmo Monte Carlo della catena di Markov attraverso specifiche dimensioni latenti. Di seguito vediamo che gli effetti dell'istruttore specifico effettivamente si allontanano in modo significativo dal loro stato iniziale ed esplorano lo spazio degli stati. Il grafico della traccia indica anche che gli effetti differiscono tra gli istruttori ma con un comportamento di miscelazione simile.
for i in range(7):
plt.plot(effect_instructors_samples[:, i])
plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()
Critica
Sopra, abbiamo montato il modello. Ora esaminiamo la critica del suo adattamento utilizzando i dati, che ci consentono di esplorare e comprendere meglio il modello. Una di queste tecniche è un grafico residuo, che traccia la differenza tra le previsioni del modello e la verità fondamentale per ogni punto dati. Se il modello fosse corretto, la loro differenza dovrebbe essere una distribuzione normale standard; eventuali deviazioni da questo modello nel grafico indicano un disadattamento del modello.
Costruiamo il grafico residuo formando prima la distribuzione predittiva a posteriori sulle valutazioni, che sostituisce la distribuzione precedente sugli effetti casuali con i suoi dati di addestramento successivi. In particolare, eseguiamo il modello in avanti e intercettiamo la sua dipendenza dagli effetti casuali precedenti con le loro medie posteriori dedotte.²
lmm_test = lmm_jointdist(features_test)
[
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
] = [
np.mean(x, axis=0).astype(np.float32) for x in [
effect_students_samples,
effect_instructors_samples,
effect_departments_samples
]
]
# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
value=(
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
))
ratings_prediction = ratings_posterior.mean()
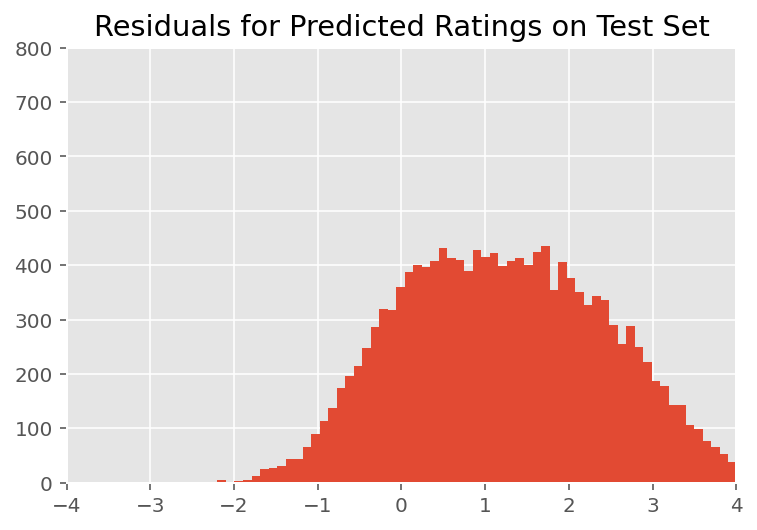
All'ispezione visiva, i residui sembrano in qualche modo distribuiti in modo standard-normale. Tuttavia, l'adattamento non è perfetto: c'è una massa di probabilità maggiore nelle code rispetto a una distribuzione normale, il che indica che il modello potrebbe migliorare il suo adattamento rilassando le sue ipotesi di normalità.
In particolare, anche se è più comune l'uso di una distribuzione normale ai rating del modello nel InstEval set di dati, uno sguardo più attento ai dati rivela che i rating di valutazione corso sono infatti valori ordinali da 1 a 5. Questo suggerisce che dovremmo utilizzare una distribuzione ordinale, o anche categoriale se abbiamo dati sufficienti per buttare via l'ordinamento relativo. Questa è una modifica di una riga al modello sopra; lo stesso codice di inferenza è applicabile.
plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()
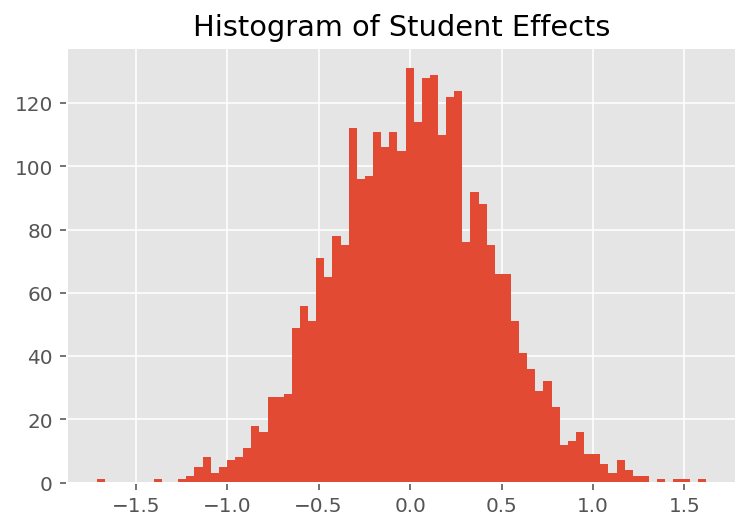
Per esplorare il modo in cui il modello effettua previsioni individuali, esaminiamo l'istogramma degli effetti per studenti, docenti e reparti. Questo ci permette di capire come i singoli elementi nel vettore delle caratteristiche di un punto dati tendano a influenzare il risultato.
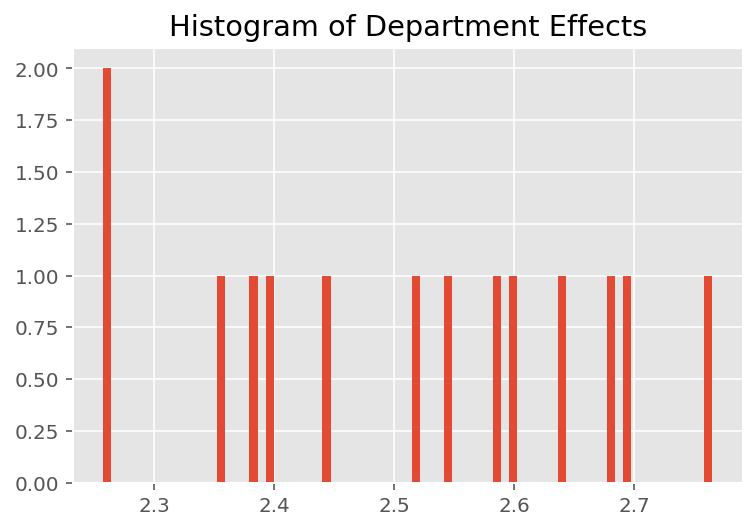
Non sorprendentemente, vediamo di seguito che ogni studente in genere ha scarso effetto sulla valutazione della valutazione di un istruttore. È interessante notare che il dipartimento a cui appartiene un istruttore ha un grande effetto.
plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()
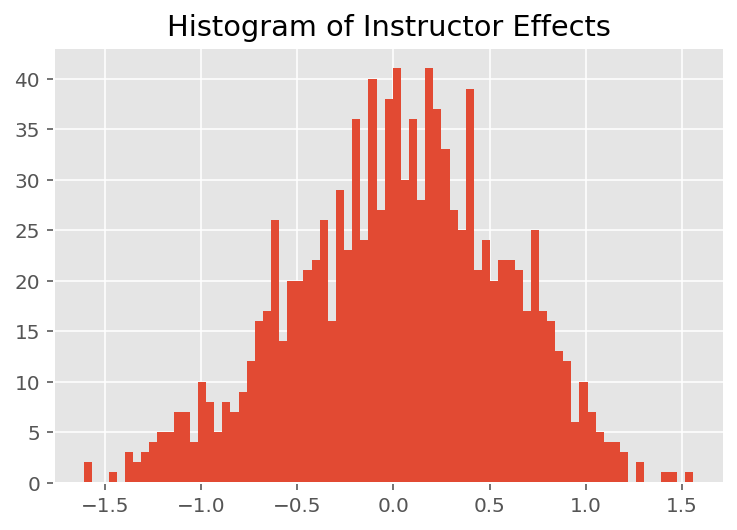
plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()
plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()
Note a piè di pagina
¹ I modelli lineari a effetto misto sono un caso speciale in cui possiamo calcolare analiticamente la sua densità marginale. Ai fini di questo tutorial, dimostriamo Monte Carlo EM, che si applica più facilmente alle densità marginali non analitiche come se la probabilità fosse estesa per essere Categorica anziché Normale.
² Per semplicità, formiamo la media della distribuzione predittiva utilizzando un solo passaggio in avanti del modello. Questo viene fatto condizionando sulla media posteriore ed è valido per i modelli lineari ad effetti misti. Tuttavia, questo non è valido in generale: la media della distribuzione predittiva a posteriori è tipicamente intrattabile e richiede di prendere la media empirica attraverso più passaggi in avanti del modello dati campioni posteriori.
Ringraziamenti
Questo tutorial è stato originariamente scritto in Edward 1.0 ( fonte ). Ringraziamo tutti coloro che hanno contribuito alla stesura e alla revisione di tale versione.
Riferimenti
Douglas Bates e Martin Machler e Ben Bolker e Steve Walker. Adattamento di modelli lineari a effetti misti utilizzando lme4. Journal of Statistical Software, 67 (1): 1-48, 2015.
Arthur P. Dempster, Nan M. Laird e Donald B. Rubin. Massima verosimiglianza da dati incompleti tramite l'algoritmo EM. Ufficiale della Royal Statistical Society, Serie B (metodologica), 1-38, 1977.
Andrew Gelman e Jennifer Hill. Analisi dei dati mediante regressione e modelli multilivello/gerarchici. Cambridge University Press, 2006.
David A. Harville. Approcci di massima verosimiglianza alla stima della componente della varianza e ai problemi correlati. Ufficiale American Statistical Association, 72 (358): 320-338, 1977.
Michele I. Giordano. Introduzione ai modelli grafici. Relazione tecnica, 2003.
Nan M. Laird e James Ware. Modelli ad effetti casuali per dati longitudinali. Biometria, 963-974, 1982.
Greg Wei e Martin A. Tanner. Un'implementazione Monte Carlo dell'algoritmo EM e degli algoritmi di aumento dei dati del povero. Ufficiale American Statistical Association, 699-704, 1990.
