 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
In questo quaderno, esploreremo TensorFlow Distributions (TFD in breve). L'obiettivo di questo quaderno è di farti salire delicatamente la curva di apprendimento, inclusa la comprensione della gestione delle forme tensoriali da parte di TFD. Questo quaderno cerca di presentare esempi prima piuttosto che concetti astratti. Presenteremo prima modi semplici canonici per fare le cose e salveremo la vista astratta più generale fino alla fine. Se siete il tipo che preferisce un tutorial più astratto e-stile di riferimento, controlla Capire tensorflow Distribuzioni Forme . Se avete domande circa il materiale qui, non esitate a contatto (o partecipare) la probabilità mailing list tensorflow . Siamo felici di aiutarti.
Prima di iniziare, è necessario importare le librerie appropriate. La nostra biblioteca generale è tensorflow_probability . Per convenzione, in genere si riferisce alla biblioteca distribuzioni come tfd .
Tensorflow Desideroso è un ambiente di esecuzione imperativo per tensorflow. In TensorFlow desideroso, ogni operazione TF viene immediatamente valutata e produce un risultato. Ciò è in contrasto con la modalità "grafico" standard di TensorFlow, in cui le operazioni TF aggiungono nodi a un grafico che viene successivamente eseguito. L'intero quaderno è scritto usando TF Eager, anche se nessuno dei concetti presentati qui si basa su questo e TFP può essere utilizzato in modalità grafico.
import collections
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
try:
tf.compat.v1.enable_eager_execution()
except ValueError:
pass
import matplotlib.pyplot as plt
Distribuzioni univariate di base
Entriamo subito e creiamo una distribuzione normale:
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
Ne possiamo trarre un campione:
n.sample()
<tf.Tensor: shape=(), dtype=float32, numpy=0.25322816>
Possiamo prelevare più campioni:
n.sample(3)
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4658079, -0.5653636, 0.9314412], dtype=float32)>
Possiamo valutare un log prob:
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
Possiamo valutare più probabilità log:
n.log_prob([0., 2., 4.])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.9189385, -2.9189386, -8.918939 ], dtype=float32)>
Abbiamo una vasta gamma di distribuzioni. Proviamo un Bernoulli:
b = tfd.Bernoulli(probs=0.7)
b
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[] event_shape=[] dtype=int32>
b.sample()
<tf.Tensor: shape=(), dtype=int32, numpy=1>
b.sample(8)
<tf.Tensor: shape=(8,), dtype=int32, numpy=array([1, 0, 0, 0, 1, 0, 1, 0], dtype=int32)>
b.log_prob(1)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.35667497>
b.log_prob([1, 0, 1, 0])
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.35667497, -1.2039728 , -0.35667497, -1.2039728 ], dtype=float32)>
Distribuzioni multivariate
Creeremo una normale multivariata con una covarianza diagonale:
nd = tfd.MultivariateNormalDiag(loc=[0., 10.], scale_diag=[1., 4.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
Confrontando questo con la normale univariata che abbiamo creato in precedenza, cosa c'è di diverso?
tfd.Normal(loc=0., scale=1.)
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
Vediamo che la univariata normale ha un event_shape di () , che indica è una distribuzione scalare. Il normale multivariata ha un event_shape di 2 , indicando la [eventi] base (https://en.wikipedia.org/wiki/Event_ (probability_theory)) di questa distribuzione è bidimensionale.
Il campionamento funziona come prima:
nd.sample()
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.2489667, 15.025171 ], dtype=float32)>
nd.sample(5)
<tf.Tensor: shape=(5, 2), dtype=float32, numpy=
array([[-1.5439653 , 8.9968405 ],
[-0.38730723, 12.448896 ],
[-0.8697963 , 9.330035 ],
[-1.2541095 , 10.268944 ],
[ 2.3475595 , 13.184147 ]], dtype=float32)>
nd.log_prob([0., 10])
<tf.Tensor: shape=(), dtype=float32, numpy=-3.2241714>
Le normali multivariate in generale non hanno covarianza diagonale. TFD offre diversi modi per creare normali multivariati, inclusa una specifica di covarianza completa, che utilizziamo qui.
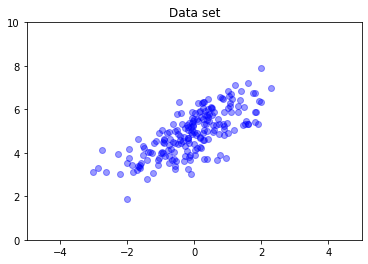
nd = tfd.MultivariateNormalFullCovariance(
loc = [0., 5], covariance_matrix = [[1., .7], [.7, 1.]])
data = nd.sample(200)
plt.scatter(data[:, 0], data[:, 1], color='blue', alpha=0.4)
plt.axis([-5, 5, 0, 10])
plt.title("Data set")
plt.show()
Distribuzioni multiple
La nostra prima distribuzione Bernoulli rappresentava il lancio di una singola moneta da fiera. Possiamo anche creare una serie di distribuzioni di Bernoulli indipendenti, ciascuno con i propri parametri, in una singola Distribution oggetto:
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
È importante essere chiari su cosa significa. La chiamata sopra definisce tre distribuzioni indipendenti Bernoulli, che capita di essere contenuti nella stessa Python Distribution oggetto. Le tre distribuzioni non possono essere manipolate singolarmente. Si noti come il batch_shape è (3,) , che indica un lotto di tre distribuzioni, e event_shape è () , indicando le singole distribuzioni hanno uno spazio evento univariata.
Se chiamiamo sample , otteniamo un campione da tutti e tre:
b3.sample()
<tf.Tensor: shape=(3,), dtype=int32, numpy=array([0, 1, 1], dtype=int32)>
b3.sample(6)
<tf.Tensor: shape=(6, 3), dtype=int32, numpy=
array([[1, 0, 1],
[0, 1, 1],
[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0]], dtype=int32)>
Se chiamiamo prob , (questo ha la stessa semantica Figura come log_prob ; utilizziamo prob con questi piccoli esempi Bernoulli per chiarezza, anche se log_prob è solitamente preferito nelle applicazioni) possiamo passare un vettore e valutare la probabilità di ogni moneta cedevole tale valore :
b3.prob([1, 1, 0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.29999998], dtype=float32)>
Perché l'API include la forma batch? Semanticamente, si potrebbe svolgere le stesse calcoli con la creazione di un elenco di distribuzioni e l'iterazione di loro con una for ciclo (almeno in modalità Eager, in modalità grafico TF avresti bisogno di un tf.while anello). Tuttavia, avere un insieme (potenzialmente ampio) di distribuzioni parametrizzate identiche è estremamente comune e l'uso di calcoli vettoriali, ove possibile, è un ingrediente chiave per essere in grado di eseguire calcoli veloci utilizzando acceleratori hardware.
Utilizzo di Indipendente per aggregare i batch agli eventi
Nel paragrafo precedente, abbiamo creato b3 , una singola Distribution oggetto che rappresentava tre lanci della moneta. Se abbiamo chiamato b3.prob su un vettore \(v\), il \(i\)'th entrata era la probabilità che la \(i\)esima moneta assume valore \(v[i]\).
Supponiamo invece di voler specificare una distribuzione "congiunta" su variabili casuali indipendenti della stessa famiglia sottostante. Questo è un oggetto diverso matematicamente, dal fatto che per questa nuova distribuzione, prob su un vettore \(v\) restituirà un singolo valore che rappresenta la probabilità che l'intero set di monete corrisponde al vettore \(v\).
Come lo realizziamo? Usiamo una distribuzione "ordine superiore" chiamato Independent , che prende una distribuzione e produce una nuova distribuzione con la forma lotto spostati nella forma dell'evento:
b3_joint = tfd.Independent(b3, reinterpreted_batch_ndims=1)
b3_joint
<tfp.distributions.Independent 'IndependentBernoulli' batch_shape=[] event_shape=[3] dtype=int32>
Confrontare la forma a quello dell'originale b3 :
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
Come promesso, si vede che quella Independent è spostato la forma dei lotti nella forma dell'evento: b3_joint è una singola distribuzione ( batch_shape = () ) nel corso di un evento di spazio tridimensionale ( event_shape = (3,) ).
Controlliamo la semantica:
b3_joint.prob([1, 1, 0])
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999998>
Un modo alternativo per ottenere lo stesso risultato sarebbe di probabilità di calcolo utilizzando b3 e fare la riduzione manualmente moltiplicando (o, nel caso più comune in cui si utilizzano le probabilità di registro, sommando):
tf.reduce_prod(b3.prob([1, 1, 0]))
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999994>
Indpendent permette all'utente di rappresentare in modo più esplicito il concetto desiderato. Consideriamo questo estremamente utile, sebbene non sia strettamente necessario.
Fatti divertenti:
-
b3.sampleeb3_joint.samplehanno diverse implementazioni concettuali, ma uscite indistinguibili: la differenza tra un lotto di distribuzioni indipendenti e una singola distribuzione creata dal batch utilizzandoIndependentappare quando calcolo probabilites, non quando il campionamento. -
MultivariateNormalDiagpotrebbe essere banalmente implementato utilizzando gli scalariNormaleIndependentdistribuzioni (non è effettivamente implementata in questo modo, ma potrebbe essere).
Lotti di distribuzioni multivariate
Creiamo un batch di tre normali multivariate bidimensionali a covarianza completa:
nd_batch = tfd.MultivariateNormalFullCovariance(
loc = [[0., 0.], [1., 1.], [2., 2.]],
covariance_matrix = [[[1., .1], [.1, 1.]],
[[1., .3], [.3, 1.]],
[[1., .5], [.5, 1.]]])
nd_batch
<tfp.distributions.MultivariateNormalFullCovariance 'MultivariateNormalFullCovariance' batch_shape=[3] event_shape=[2] dtype=float32>
Vediamo batch_shape = (3,) , quindi ci sono tre normali multivariate indipendenti, e event_shape = (2,) , quindi ogni multivariata normale è bidimensionale. In questo esempio, le singole distribuzioni non hanno elementi indipendenti.
Il campionamento funziona:
nd_batch.sample(4)
<tf.Tensor: shape=(4, 3, 2), dtype=float32, numpy=
array([[[ 0.7367498 , 2.730996 ],
[-0.74080074, -0.36466932],
[ 0.6516018 , 0.9391426 ]],
[[ 1.038303 , 0.12231752],
[-0.94788766, -1.204232 ],
[ 4.059758 , 3.035752 ]],
[[ 0.56903946, -0.06875849],
[-0.35127294, 0.5311631 ],
[ 3.4635801 , 4.565582 ]],
[[-0.15989424, -0.25715637],
[ 0.87479895, 0.97391707],
[ 0.5211419 , 2.32108 ]]], dtype=float32)>
Poiché batch_shape = (3,) e event_shape = (2,) , si passa un tensore di forma (3, 2) a log_prob :
nd_batch.log_prob([[0., 0.], [1., 1.], [2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.8328519, -1.7907217, -1.694036 ], dtype=float32)>
Trasmissione, alias Perché è così confuso?
Astraendo fuori quello che abbiamo fatto fino ad ora, ogni distribuzione ha una forma lotti B e una forma evento E . Lasciate BE sia la concatenazione delle forme di eventi:
- Per le distribuzioni scalari univariate
neb,BE = ().. - Per le normali multivariate bidimensionali
nd.BE = (2). - Sia per
b3eb3_joint,BE = (3). - Per il lotto di normali multivariate
ndb,BE = (3, 2).
Le "regole di valutazione" che abbiamo utilizzato finora sono:
- Esempio senza argomenti restituisce un tensore di forma
BE; campionamento con uno scalare n restituisce un "n daBE" tensore. -
probelog_probrimessa tensore di formaBEe restituisce risultati di formaB.
L'attuale "regola di valutazione" per prob e log_prob è più complicato, in un modo che offre un potenziale di potenza e velocità, ma anche la complessità e le sfide. La regola attuale è (essenzialmente) che l'argomento log_prob deve essere broadcastable contro BE ; eventuali dimensioni "extra" vengono conservate nell'output.
Esploriamo le implicazioni. Per il univariata normale n , BE = () , quindi log_prob aspetta uno scalare. Se passiamo log_prob un tensore di forma non vuota, quelli visualizzati come dimensioni lotti in uscita:
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
n.log_prob([0.])
<tf.Tensor: shape=(1,), dtype=float32, numpy=array([-0.9189385], dtype=float32)>
n.log_prob([[0., 1.], [-1., 2.]])
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[-0.9189385, -1.4189385],
[-1.4189385, -2.9189386]], dtype=float32)>
Turno di Let al normale multivariata bidimensionale nd (parametri modificati per scopi illustrativi):
nd = tfd.MultivariateNormalDiag(loc=[0., 1.], scale_diag=[1., 1.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
log_prob "si aspetta" un argomento di forma (2,) , ma accetterà alcuna argomentazione che le trasmissioni contro questa forma:
nd.log_prob([0., 0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
Ma possiamo passare in "più" esempi, e valutare tutta la loro log_prob 's in una sola volta:
nd.log_prob([[0., 0.],
[1., 1.],
[2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
Forse in modo meno attraente, possiamo trasmettere sulle dimensioni dell'evento:
nd.log_prob([0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
nd.log_prob([[0.], [1.], [2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
La trasmissione in questo modo è una conseguenza del nostro design "abilita la trasmissione quando possibile"; questo utilizzo è alquanto controverso e potrebbe essere potenzialmente rimosso in una versione futura di TFP.
Ora diamo un'occhiata all'esempio delle tre monete:
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
Qui, utilizzando la trasmissione per rappresentare la probabilità che ogni moneta viene testa è abbastanza intuitivo:
b3.prob([1])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.7 ], dtype=float32)>
(Confronta questo per b3.prob([1., 1., 1.]) , che avremmo di nuovo usato dove b3 è stato introdotto.)
Ora supponiamo di voler sapere, per ogni moneta, la probabilità la moneta viene testa e la probabilità che viene croce. Potremmo immaginare di provare:
b3.log_prob([0, 1])
Sfortunatamente, questo produce un errore con una traccia dello stack lunga e non molto leggibile. b3 ha BE = (3) , quindi dobbiamo passare b3.prob qualcosa broadcastable contro (3,) . [0, 1] ha forma (2) , in modo che non trasmette e crea un errore. Dobbiamo invece dire:
b3.prob([[0], [1]])
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[0.7, 0.5, 0.3],
[0.3, 0.5, 0.7]], dtype=float32)>
Come mai? [[0], [1]] ha forma (2, 1) , quindi trasmette contro forma (3) per creare una forma di trasmissione (2, 3) .
La trasmissione è piuttosto potente: ci sono casi in cui consente la riduzione dell'ordine di grandezza della quantità di memoria utilizzata e spesso riduce il codice utente. Tuttavia, può essere difficile programmare con. Se si chiama log_prob e ottiene un errore, una mancata trasmissione è quasi sempre il problema.
Andando più lontano
In questo tutorial, abbiamo (si spera) fornito una semplice introduzione. Alcuni suggerimenti per andare oltre:
-
event_shape,batch_shapeesample_shapepossono essere rango arbitrario (in questa esercitazione sono sempre o scalari o livello 1). Ciò aumenta la potenza, ma ancora una volta può portare a problemi di programmazione, soprattutto quando è coinvolta la trasmissione. Per un ulteriore deep in forma manipolazione, vedere Understanding tensorflow Distribuzioni forme . - PTF include un potente astrazione noto come
Bijectors, che in combinazione conTransformedDistribution, produce un modo composizionale flessibile per creare facilmente nuove distribuzioni che sono trasformazioni invertibili di distribuzioni esistenti. Cercheremo di scrivere un tutorial su questo presto, ma nel frattempo, controlla la documentazione
