TensorFlow.org'da görüntüleyin

Google Colab'da çalıştırın

Kaynağı GitHub'da görüntüleyin

Not defterini indir

Bu defteri TensorFlow Olasılığını öğrenmek için bir vaka çalışması olarak yazdım. Çözmeyi seçtiğim problem, 2 boyutlu ortalama 0 Gauss rastgele değişken örnekleri için bir kovaryans matrisi tahmin etmektir. Sorunun birkaç güzel özelliği var:

• Kovaryans için önce ters bir Wishart kullanırsak (ortak bir yaklaşım), sorunun analitik bir çözümü vardır, böylece sonuçlarımızı kontrol edebiliriz.
• Sorun, bazı ilginç karmaşıklıklar ekleyen kısıtlı bir parametrenin örneklenmesini içerir.
• En basit çözüm, en hızlı çözüm değildir, bu nedenle yapılacak bazı optimizasyon çalışmaları vardır.

Gittikçe deneyimlerimi yazmaya karar verdim. TFP'nin ince noktalarına kafa yormam biraz zaman aldı, bu nedenle bu dizüstü bilgisayar oldukça basit bir şekilde başlıyor ve ardından yavaş yavaş daha karmaşık TFP özelliklerine geçiyor. Yol boyunca birçok sorunla karşılaştım ve hem bunları tanımlamama yardımcı olan süreçleri hem de sonunda bulduğum geçici çözümleri yakalamaya çalıştım. Ben (Emin bireysel adımlar doğru yapmak için testlerin bir sürü dahil) detay bir sürü içerecek şekilde çalıştık.

Neden TensorFlow Olasılığını öğrenmelisiniz?

TensorFlow Probability'yi projem için birkaç nedenden dolayı çekici buldum:

• TensorFlow olasılığı, bir not defterinde etkileşimli olarak karmaşık modeller geliştirmek için prototip oluşturmanıza olanak tanır. Kodunuzu etkileşimli ve birim testleri ile test edebileceğiniz küçük parçalara ayırabilirsiniz.
• Ölçeklendirmeye hazır olduğunuzda, TensorFlow'un birden çok makinede birden çok optimize edilmiş işlemci üzerinde çalışmasını sağlamak için sahip olduğumuz tüm altyapıdan yararlanabilirsiniz.
• Son olarak, Stan'i gerçekten sevsem de hata ayıklamayı oldukça zor buluyorum. Tüm modelleme kodunuzu, kodunuzu kurcalamanıza, ara durumları incelemenize vb. izin vermek için çok az aracı olan bağımsız bir dilde yazmanız gerekir.

Dezavantajı, TensorFlow Probability'nin Stan ve PyMC3'ten çok daha yeni olmasıdır, bu nedenle belgeler devam eden bir çalışmadır ve henüz oluşturulmamış pek çok işlevsellik vardır. Ne mutlu ki, TFP'nin temelini sağlam buldum ve modüler bir şekilde tasarlanmış, bu da işlevselliğini oldukça basit bir şekilde genişletmeye olanak tanıyor. Bu not defterinde, vaka çalışmasını çözmenin yanı sıra, TFP'yi genişletmenin bazı yollarını göstereceğim.

Bu kimin için

Okuyucuların bu deftere bazı önemli ön koşullarla geldiklerini varsayıyorum. Malısın:

• Bayes çıkarımının temellerini bilir. (Eğer yoksa, gerçekten güzel bir ilk kitap İstatistiksel Yeniden Düşünmek )
• Bir MCMC örnekleme kütüphane, örneğin konusunda biraz bilgi sahibi Stan / PyMC3 / BÖCEK
• Sağlam bir kavrayışa sahip numpy (Bir iyi intro Python Veri Analizi için )
• İle en az geçen aşinalık az mı TensorFlow , ama mutlaka uzmanlığı. ( Öğrenme TensorFlow iyidir, ama TensorFlow en hızlı evrimi araçlarının çoğu kitap biraz tarihli olacağını. Stanford CS20 sahası da iyidir.)

İlk girişim

İşte soruna ilk girişimim. Spoiler: Benim çözümüm işe yaramıyor ve işleri yoluna koymak için birkaç kez denemem gerekecek! Süreç biraz zaman alsa da, aşağıdaki her girişim, TFP'nin yeni bir bölümünü öğrenmek için faydalı olmuştur.

Bir not: TFP şu anda ters Wishart dağılımını uygulamamaktadır (sonunda kendi ters Wishart'ımızı nasıl yuvarlayacağımızı göreceğiz), bu yüzden onun yerine sorunu, önce bir Wishart kullanarak hassas bir matris tahmin etme sorunuyla değiştireceğim.

import collections
import math
import os
import time

import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

Adım 1: gözlemleri bir araya getirin

Buradaki verilerimin tamamı sentetik, bu yüzden bu gerçek dünyadaki bir örnekten biraz daha düzenli görünecek. Ancak, kendinize ait bazı sentetik veriler üretememeniz için hiçbir neden yok.

İpucu: modeli şeklinde karar verdikten sonra, bazı parametre değerleri almak ve bazı sentetik verileri oluşturmak için seçtiğiniz model kullanabilir. Uygulamanızın akıl sağlığı kontrolü olarak, tahminlerinizin seçtiğiniz parametrelerin gerçek değerlerini içerdiğini doğrulayabilirsiniz. Hata ayıklama/test döngünüzü daha hızlı hale getirmek için modelinizin basitleştirilmiş bir sürümünü düşünebilirsiniz (örneğin daha az boyut veya daha az örnek kullanın).

İpucu: NumPy diziler gibi gözlemlerle işin en kolay yoldur. Unutulmaması gereken önemli bir nokta, NumPy'nin varsayılan olarak float64'leri kullanması, TensorFlow'un ise varsayılan olarak float32'leri kullanmasıdır.

Genel olarak, TensorFlow işlemleri, tüm bağımsız değişkenlerin aynı türe sahip olmasını ister ve türleri değiştirmek için açık veri dökümü yapmanız gerekir. Float64 gözlemleri kullanıyorsanız, çok sayıda yayın işlemi eklemeniz gerekir. NumPy, aksine, otomatik olarak yayınlamayı halledecektir. Dolayısıyla, bu kullanım float64 için TensorFlow zorlamak için daha float32 içine Numpy verileri dönüştürmek için çok daha kolaydır.

Bazı parametre değerleri seçin

# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
    np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)

# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))

[[4.  1.8]
 [1.8 1. ]]
eigenvalues:  [4.843075   0.15692513]

Bazı sentetik gözlemler oluşturun

Not TensorFlow Olasılık verilerin başlangıç boyut (lar) bir numunesi, endeksleri temsil kuralı kullanan, ve verilerin son boyut (lar) da örneklerin boyutluluk temsil eder.

Burada uzunlukta bir vektördür, her biri 100 örnek, 2. Biz bir dizi oluşturmak gerekir isteyen my_data şeklinde (100, 2) ile yıkanmıştır. my_data[i, :] olan \(i\)inci örnek, ve uzunluğu 2 bir vektördür.

(Yapmayı unutmayın my_data tip float32 var!)

# Set the seed so the results are reproducible.
np.random.seed(123)

# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
    mean=true_mean, cov=true_cov, size=100,
    check_valid='ignore').astype(np.float32)

my_data.shape

(100, 2)

Akıl sağlığı gözlemleri kontrol edin

Potansiyel bir hata kaynağı, sentetik verilerinizi karıştırmaktır! Birkaç basit kontrol yapalım.

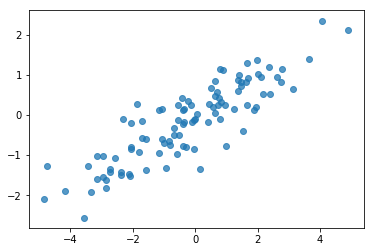
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()

print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)

mean of observations: [-0.24009615 -0.16638893]
true mean: [0. 0.]

print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)

covariance of observations:
 [[3.95307734 1.68718486]
 [1.68718486 0.94910269]]
true covariance:
 [[4.  1.8]
 [1.8 1. ]]

Tamam, örneklerimiz makul görünüyor. Sonraki adım.

Adım 2: NumPy'de olabilirlik işlevini uygulayın

TF Olasılığı'nda MCMC örneklememizi gerçekleştirmek için yazmamız gereken ana şey, bir günlük olabilirlik işlevidir. Genelde TF yazmak NumPy'den biraz daha zor, bu yüzden NumPy'de bir ilk uygulama yapmayı faydalı buluyorum. Ben 2 adet, karşılık geldiğini veri olabilirlik fonksiyonu içine olabilirlik fonksiyonunu bölmek için gidiyorum \(P(data | parameters)\) ve önceki olabilirlik fonksiyonu karşılık bu \(P(parameters)\).

Amaç yalnızca test için bazı değerler oluşturmak olduğundan, bu NumPy işlevlerinin süper optimize edilmesi/vektörleştirilmesi gerekmediğini unutmayın. Doğruluk en önemli husustur!

İlk önce veri günlüğü olasılık parçasını uygulayacağız. Bu oldukça basit. Hatırlanması gereken tek şey, hassas matrislerle çalışacağımızdır, bu yüzden buna göre parametreleştireceğiz.

def log_lik_data_numpy(precision, data):
  # np.linalg.inv is a really inefficient way to get the covariance matrix, but
  # remember we don't care about speed here
  cov = np.linalg.inv(precision)
  rv = scipy.stats.multivariate_normal(true_mean, cov)
  return np.sum(rv.logpdf(data))

# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)

-280.81822950593767

Biz posterior analitik çözümü vardır çünkü (bkz hassas matris için önce bir Wishart kullanacağız eşlenik sabıkası Wikipedia'nın kullanışlı masa ).

Wishart dağılımı 2 parametresi vardır:

• serbestlik derecesi sayısının (etiketli \(\nu\) Wikipedia)
• bir ölçek matrisi (etiketli \(V\) Wikipedia)

Parametrelerle bir Wishart dağıtım için ortalama \(\nu, V\) olan \(E[W] = \nu V\)ve varyans ise \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)

Bazı faydalı sezgi: Eğer üreten bir Wishart örnek oluşturabilir \(\nu\) bağımsız çizer \(x_1 \ldots x_{\nu}\) 0 ortalama ve ortak bir çok değişkenli normal rastgele değişken \(V\) ve daha sonra toplam oluşturan \(W = \sum_{i=1}^{\nu} x_i x_i^T\).

Eğer bunları bölerek Wishart örnekleri rescale Eğer \(\nu\), size örnek kovaryans matrisi olsun \(x_i\). Bu örnek kovaryans matrisi doğru baksın \(V\) olarak \(\nu\) artar. Tüm \(\nu\) küçük, örnek kovaryans matrisi içinde çok varyasyon, bu kadar küçük bir değer olduğu \(\nu\) zayıf önsel ve büyük değerlere karşılık gelmektedir \(\nu\) güçlü önsel tekabül eder. Not o \(\nu\) en azından sen örnekleme veya tekil matrisleri elde edersiniz alan boyutu olarak büyük olarak olmalıdır.

Biz kullanacağız \(\nu = 3\) biz zayıf öncesinde zorunda ve biz götürürüz \(V = \frac{1}{\nu} I\) (ortalama olduğunu hatırlama kimliğine ilişkin bizim kovaryans tahmini çeker \(\nu V\)).

PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF

def log_lik_prior_numpy(precision):
  rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
  return rv.logpdf(precision)

# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)

-9.103606346649766

Wishart dağılımı bilinen ortalama bir değişkenli normal hassas matrisi tahmin etmek için eşlenik önce olduğu \(\mu\).

Önceki Wishart parametrelerdir varsayalım \(\nu, V\) ve sahip olduğumuz \(n\) bizim değişkenli normal, gözlemlerini \(x_1, \ldots, x_n\). Posterior parametrelerdir \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).

n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
                       (v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))

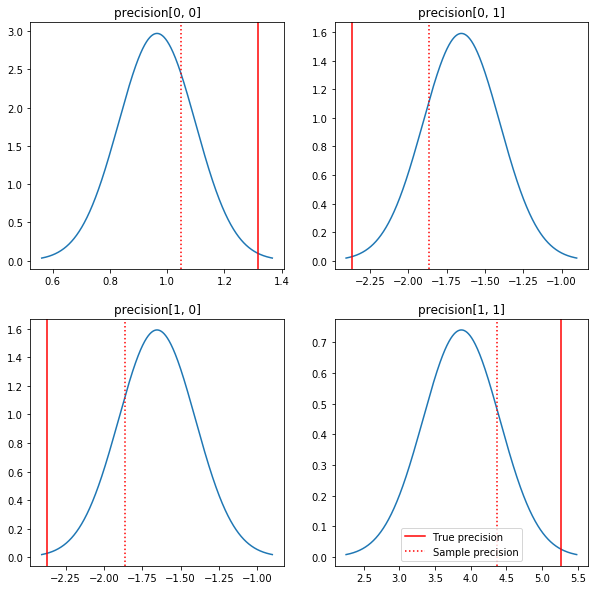
Posteriorların ve gerçek değerlerin hızlı bir grafiği. Posteriorların örnek posteriorlarına yakın olduğunu ancak özdeşliğe doğru biraz küçüldüğünü unutmayın. Ayrıca gerçek değerlerin posterior modundan oldukça uzak olduğuna da dikkat edin - bunun nedeni muhtemelen öncekinin verilerimiz için çok iyi bir eşleşme olmamasıdır. Gerçek bir sorun biz büyük olasılıkla kovaryans durumunda öncesinde Wishart ters ölçekli bir gibi bir şey ile daha iyi yapabileceklerini (örneğin bkz, Andrew Gelman en şerh konuda), ama sonra güzel bir analitik posterior olmazdı.

sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    loc = posterior_mean[i, j]
    scale = posterior_sd[i, j]
    xmin = loc - 3.0 * scale
    xmax = loc + 3.0 * scale
    x = np.linspace(xmin, xmax, 1000)
    y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
    ax.plot(x, y)
    ax.axvline(true_precision[i, j], color='red', label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()

Adım 3: Olabilirlik işlevini TensorFlow'da uygulayın

Spoiler: İlk denememiz işe yaramayacak; neden hakkında aşağıda konuşacağız.

İpucu: Kullanım TensorFlow istekli modu olabilirlik fonksiyonları geliştirerek. Hevesli modu daha numpy gibi TF davranmak yapar - her şey yürütür hemen, kullanmak zorunda yerine etkileşimli hata ayıklama böylece Session.run() . Notlara bakın burada .

Ön Hazırlık: Dağıtım sınıfları

TFP, günlük olasılıklarımızı oluşturmak için kullanacağımız bir dağıtım sınıfları koleksiyonuna sahiptir. Unutulmaması gereken bir şey, bu sınıfların yalnızca tek örnekler yerine örneklerin tensörleriyle çalıştığıdır - bu, vektörleştirmeye ve ilgili hızlandırmalara izin verir.

Bir dağıtım, bir tensör numunesi ile 2 farklı şekilde çalışabilir. Bu 2 yolu, tek bir skaler parametreli bir dağılımı içeren somut bir örnekle göstermek en basitidir. Ben kullanacağız Poisson bir sahip dağıtım, rate parametresi.

• Biz için tek bir değere sahip bir Poisson oluşturmak halinde rate parametresi, onun için bir çağrı sample() yöntemi, tek bir değer döndürür. Bu değer bir denir event ve bu durumda olayların tümü skalerler bulunmaktadır.
• Biz değerlerinin bir tensör bir Poisson oluşturmak halinde rate parametresi, onun için bir çağrı sample() yöntemi artık hızı tensörünün her değer için bir çok değerler verir. Bu amaca, bağımsız Poissons bir toplama, kendi hızı ile her biri hareket eder ve değerlerin her bir çağrı tarafından döndürülen sample() bu Poissons birine karşılık gelir. Bağımsız ama aynı dağıtılan olayların Bu koleksiyon denir batch .
• sample() metodu alır sample_shape boş başlığın için varsayılan olarak parametre. Olmayan bir boş değer geçen sample_shape birden çok toplu dönen örnekteki sonuçlar. Serilerin Bu koleksiyon denir sample .

Bir dağıtımın log_prob() metodu ne paralel bir şekilde veri tüketir sample() o oluşturur. log_prob() için birden çok numune için olasılıkları, yani olay bağımsız toplu döndürür.

• Biz skaler ile oluşturuldu bizim Poisson nesne varsa rate , her parti bir skaler ve biz örneklerin bir tensör başarılı olursa, biz günlük olasılıklarının aynı büyüklükteki bir tensörünü dışarı alırsınız.
• Biz şekli bir tensör ile oluşturuldu bizim Poisson nesne varsa T ait rate değerlerinin, her bir parti şekli bir tensör olan T . D, T şeklinde örneklerin bir tensörünü geçirirsek, D, T şeklinde bir log olasılık tensörü çıkaracağız.

Aşağıda bu durumları gösteren bazı örnekler verilmiştir. Bkz Bu defteri etkinlikler, gruplar halinde ve şekiller üzerinde daha ayrıntılı öğretici için.

# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))

# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters.  Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))

print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())

iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385]
draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]

Veri günlüğü olasılığı

İlk önce veri günlüğü olabilirlik fonksiyonunu uygulayacağız.

VALIDATE_ARGS = True
ALLOW_NAN_STATS = False

NumPy durumundan önemli bir fark, TensorFlow olabilirlik işlevimizin yalnızca tek matrisler yerine hassas matrislerin vektörlerini işlemesi gerekmesidir. Birden çok zincirden örnek aldığımızda parametre vektörleri kullanılacaktır.

Bir grup hassas matrisle (yani zincir başına bir matris) çalışan bir dağıtım nesnesi oluşturacağız.

Verilerimizin günlük olasılıklarını hesaplarken, verilerimizin parametrelerimizle aynı şekilde çoğaltılması gerekir, böylece her toplu iş değişkeni için bir kopya olur. Çoğaltılan verilerimizin şeklinin aşağıdaki gibi olması gerekir:

[sample shape, batch shape, event shape]

Bizim durumumuzda olay şekli 2'dir (2 boyutlu Gausslarla çalıştığımız için). 100 numunemiz olduğu için numune şekli 100'dür. Parti şekli, üzerinde çalıştığımız hassas matrislerin sayısı olacaktır. Olabilirlik işlevini her çağırdığımızda verileri çoğaltmak israftır, bu nedenle verileri önceden çoğaltacağız ve çoğaltılmış sürüme geçeceğiz.

Not Bu verimsiz bir uygulama olduğunu: MultivariateNormalFullCovariance biz sonunda optimizasyon bölümünde bahsedeceğiz bazı alternatifler pahalı görecelidir.

def log_lik_data(precisions, replicated_data):
  n = tf.shape(precisions)[0]  # number of precision matrices
  # We're estimating a precision matrix; we have to invert to get log
  # probabilities.  Cholesky inversion should be relatively efficient,
  # but as we'll see later, it's even better if we can avoid doing the Cholesky
  # decomposition altogether.
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data).  We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)

(100, 2, 2)

İpucu: Bir şey benim TensorFlow fonksiyonlarının küçük mantıklı denetimleri yazıyor son derece yararlı olduğu tespit ettik. TF'de vektörleştirmeyi bozmak gerçekten çok kolay, bu nedenle daha basit NumPy işlevlerine sahip olmak, TF çıktısını doğrulamak için harika bir yoldur. Bunları küçük birim testleri olarak düşünün.

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

Önceki günlük olasılığı

Veri kopyalama konusunda endişelenmemize gerek olmadığı için önceki daha kolaydır.

@tf.function(autograph=False)
def log_lik_prior(precisions):
  rv_precision = tfd.WishartTriL(
      df=PRIOR_DF,
      scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions)

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]))
  print('tensorflow:', lik_tf[i])

0
numpy: -2.2351873809649625
tensorflow: -2.2351875
1
numpy: -9.103606346649766
tensorflow: -9.103608

Ortak günlük olabilirlik işlevini oluşturun

Yukarıdaki veri günlüğü olabilirlik işlevi gözlemlerimize bağlıdır, ancak örnekleyici bunlara sahip olmayacaktır. Bir [kapatma](https://en.wikipedia.org/wiki/Closure_(computer_programming) kullanarak global bir değişken kullanmadan bağımlılıktan kurtulabiliriz.Kapatmalar, bir kullanıcının ihtiyaç duyduğu değişkenleri içeren bir ortam oluşturan bir dış işlev içerir. iç fonksiyon.

def get_log_lik(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik(precision):
    return log_lik_data(precision, replicated_data) + log_lik_prior(precision)

  return _log_lik

Adım 4: Örnek

Tamam, örnekleme zamanı! İşleri basit tutmak için sadece 1 zincir kullanacağız ve başlangıç ​​noktası olarak birim matrisini kullanacağız. İşleri daha sonra daha dikkatli yapacağız.

Yine, bu işe yaramayacak - bir istisna alacağız.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.expand_dims(tf.eye(2), axis=0)

  # Use expand_dims because we want to pass in a tensor of starting values
  log_lik_fn = get_log_lik(my_data, n_chains=1)

  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
     num_results=num_results,
     num_burnin_steps=num_burnin_steps,
     current_state=[
         init_precision,
     ],
     kernel=tfp.mcmc.HamiltonianMonteCarlo(
         target_log_prob_fn=log_lik_fn,
         step_size=0.1,
         num_leapfrog_steps=3),
     trace_fn=None,
     seed=123)
  return states

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

Cholesky decomposition was not successful. The input might not be valid.
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]

Function call stack:
sample
...
Function call stack:
sample

Sorunu belirleme

InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. Bu süper yardımcı değil. Bakalım neler olduğu hakkında daha fazla şey öğrenebilecek miyiz.

• Her adımın parametrelerini yazdıracağız, böylece işlerin başarısız olduğu değeri görebiliriz.
• Belirli sorunlara karşı korunmak için bazı iddialar ekleyeceğiz.

İddialar yanıltıcıdır çünkü bunlar TensorFlow işlemleridir ve bunların yürütülmesine ve grafikten optimize edilmemesine dikkat etmemiz gerekir. Okumaya It yetmeyecek bu bakış Eğer TF iddialarına aşina değilseniz TensorFlow hata ayıklama. Açıkça kullanarak çalıştırmak için iddialarını zorlayabilir tf.control_dependencies (aşağıda kodda yorumlara bakınız).

TensorFlow doğal Print Bir operasyon var ve bunu çalıştırır sağlamak için bazı dikkat çekmek gerekir - fonksiyon iddialarına aynı davranışı vardır. Print çıkış gönderilir: bir deftere çalışırken ek baş ağrısı neden olur stderr ve stderr hücrede gösterilmez. Biz burada bir hile kullanacağız: kullanmak yerine tf.Print , biz yoluyla kendi TensorFlow baskı işlemi oluştururuz tf.pyfunc . İddialarda olduğu gibi, yöntemimizin çalıştığından emin olmalıyız.

def get_log_lik_verbose(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  def _log_lik(precisions):
    # An internal method we'll make into a TensorFlow operation via tf.py_func
    def _print_precisions(precisions):
      print('precisions:\n', precisions)
      return False  # operations must return something!
    # Turn our method into a TensorFlow operation
    print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)

    # Assertions are also operations, and some care needs to be taken to ensure
    # that they're executed
    assert_op = tf.assert_equal(
        precisions, tf.linalg.matrix_transpose(precisions),
        message='not symmetrical', summarize=4, name='symmetry_check')

    # The control_dependencies statement forces its arguments to be executed
    # before subsequent operations
    with tf.control_dependencies([print_op, assert_op]):
      return (log_lik_data(precisions, replicated_data) +
              log_lik_prior(precisions))

  return _log_lik

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.eye(2)[tf.newaxis, ...]
  log_lik_fn = get_log_lik_verbose(my_data)
  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          init_precision,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=None,
      seed=123)

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[ 0.24315196 -0.2761638 ]
  [-0.33882257  0.8622    ]]]
 assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]

Function call stack:
sample
...
Function call stack:
sample

Bu neden başarısız

Örnekleyicinin denediği ilk yeni parametre değeri asimetrik bir matristir. Bu, yalnızca simetrik (ve pozitif tanımlı) matrisler için tanımlandığından, Cholesky ayrıştırmasının başarısız olmasına neden olur.

Buradaki sorun, ilgilendiğimiz parametrenin bir hassas matris olması ve hassas matrislerin gerçek, simetrik ve pozitif tanımlı olması gerektiğidir. Örnekleyici bu kısıtlama hakkında hiçbir şey bilmiyor (muhtemelen gradyanlar dışında), bu nedenle örnekleyicinin geçersiz bir değer önermesi, özellikle adım boyutu büyükse bir istisnaya yol açması tamamen mümkündür.

Hamiltonyen Monte Carlo örnekleyici ile, gradyan parametreleri geçersiz bölgelerden uzak tutması gerektiğinden, ancak küçük adım boyutları yavaş yakınsama anlamına geldiğinden, çok küçük bir adım boyutu kullanarak sorunu çözebiliriz. Gradyanlar hakkında hiçbir şey bilmeyen bir Metropolis-Hastings örnekleyicisi ile ölüme mahkumuz.

Sürüm 2: kısıtlanmamış parametrelere yeniden parametrelendirme

Yukarıdaki problemin basit bir çözümü var: Modelimizi, yeni parametrelerin artık bu kısıtlamalara sahip olmayacağı şekilde yeniden parametrelendirebiliriz. TFP, tam da bunu yapmak için yararlı bir araç seti - bijektörler - sağlar.

Bijektörlerle yeniden parametrelendirme

Hassas matrisimiz gerçek ve simetrik olmalıdır; bu kısıtlamalara sahip olmayan alternatif bir parametreleştirme istiyoruz. Başlangıç ​​noktası, hassas matrisin Cholesky çarpanlarına ayrılmasıdır. Cholesky faktörleri hala sınırlıdır - alt üçgenlerdir ve köşegen elemanları pozitif olmalıdır. Bununla birlikte, Cholesky faktörünün köşegenlerinin logunu alırsak, loglar artık pozitif olmak için kısıtlanmaz ve daha sonra alt üçgen kısmı 1 boyutlu bir vektöre yassılaştırırsak, artık alt üçgen kısıtlamasına sahip değiliz. . Bizim durumumuzda sonuç, kısıtlaması olmayan bir uzunluk 3 vektörü olacaktır.

( Stan manuel parametreleri üzerine kısıtlamalar çeşitli kaldırmak için dönüşümleri kullanma konusunda büyük bir bölümü vardır.)

Bu yeniden parametreleştirmenin veri günlüğü olabilirlik işlevimiz üzerinde çok az etkisi vardır - hassas matrisi geri almak için dönüşümümüzü tersine çevirmemiz yeterlidir - ancak önceki üzerindeki etki daha karmaşıktır. Belirli bir kesinlik matrisinin olasılığının Wishart dağılımı tarafından verildiğini belirledik; dönüştürülmüş matrisimizin olasılığı nedir?

Bir monoton bir fonksiyonu uygulamak durumunda hatırlayın bu \(g\) bir 1-D rastgele değişkenin \(X\), \(Y = g(X)\), yoğunluk \(Y\) ile verilir

\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]

Türev \(g^{-1}\) dönem bu şekilde hesapları \(g\) yerel birimleri değiştirir. Yüksek boyutlu, rastgele değişkenler için, düzeltici faktörü Jacobi belirleyicisi mutlak değeri \(g^{-1}\) (bakınız buraya ).

Log-öncelikli olabilirlik fonksiyonumuza ters dönüşümün bir Jacobian'ını eklememiz gerekecek. Ne mutlu ki, TFP en Bijector sınıfı bizim için bu bakabilirim.

Bijector sınıfı olasılık yoğunluk fonksiyonları değişkenleri değiştirmek için kullanılır tersi, düz fonksiyonlarını temsil etmek için kullanılır. Bijectors tüm sahip forward() yerine getirmekte olup, bir dönüşümü bu yöntemi inverse() metodu olduğu gibi ters çevirir bu ve forward_log_det_jacobian() ve inverse_log_det_jacobian() bir pdf reparaterize zaman ihtiyacımız Jacobi düzeltmeler yöntemleri.

TFP biz yoluyla kompozisyon yoluyla birleştirebilirsiniz kullanışlı bijectors bir koleksiyonunu sağlar Chain oldukça karmaşık dönüşümleri oluşturmak için operatör. Bizim durumumuzda, aşağıdaki 3 bijektörü oluşturacağız (zincirdeki işlemler sağdan sola yapılır):

1. Dönüşümümüzün ilk adımı, hassas matris üzerinde bir Cholesky çarpanlarına ayırma gerçekleştirmektir. Bunun için bir Bijector sınıfı yok; Bununla birlikte, CholeskyOuterProduct bijector 2 Cholesky faktörlerin ürün alır. Biz kullanarak bu operasyonun tersini kullanabilirsiniz Invert operatörü.
2. Bir sonraki adım, Cholesky faktörünün köşegen elemanlarının günlüğünü almaktır. Biz aracılığıyla Bunu başarmak TransformDiagonal bijector ve tersi Exp bijector.
3. Son olarak tersinin kullanılması bir vektöre matris alt üçgen kısmı dümdüz FillTriangular bijector.

# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
    # step 3: flatten the lower triangular portion of the matrix
    tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
    # step 2: take the log of the diagonals    
    tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
    # step 1: decompose the precision matrix into its Cholesky factors
    tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])

# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)

# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)

print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()

print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())

single input:
m:
 [[1. 2.]
 [2. 8.]]
precision_to_unconstrained(m):
 [0.6931472 2.        0.       ]
inverse(precision_to_unconstrained(m)):
 [[1. 2.]
 [2. 8.]]

tensor of inputs:
m2:
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]
precision_to_unconstrained(m2):
 [[0.6931472 2.        0.       ]
 [0.        0.        0.       ]]
inverse(precision_to_unconstrained(m2)):
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]

TransformedDistribution sınıfı için gerekli Jakobyan düzeltme bir dağılım için bir bijector uygulanması ve yapım işlemini otomatik hale log_prob() . Yeni önceliğimiz:

def log_lik_prior_transformed(transformed_precisions):
  rv_precision = tfd.TransformedDistribution(
      tfd.WishartTriL(
          df=PRIOR_DF,
          scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
          validate_args=VALIDATE_ARGS,
          allow_nan_stats=ALLOW_NAN_STATS),
      bijector=precision_to_unconstrained,
      validate_args=VALIDATE_ARGS)
  return rv_precision.log_prob(transformed_precisions)

# Check against the numpy implementation.  Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
    transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow: -0.84889317
1
numpy: -7.305657151741624
tensorflow: -7.305659

Veri günlüğü olasılığımız için dönüşümü tersine çevirmemiz yeterli:

precision = precision_to_unconstrained.inverse(transformed_precision)

Aslında hassas matrisin Cholesky çarpanlarına ayırmasını istediğimiz için, burada sadece kısmi tersini yapmak daha verimli olacaktır. Ancak, optimizasyonu sonraya bırakacağız ve kısmi tersini okuyucu için bir alıştırma olarak bırakacağız.

def log_lik_data_transformed(transformed_precisions, replicated_data):
  # We recover the precision matrix by inverting our bijector.  This is
  # inefficient since we really want the Cholesky decomposition of the
  # precision matrix, and the bijector has that in hand during the inversion,
  # but we'll worry about efficiency later.
  n = tf.shape(transformed_precisions)[0]
  precisions = precision_to_unconstrained.inverse(transformed_precisions)
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
    transformed_precisions, replicated_data).numpy()

for i in range(precisions.shape[0]):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

Yine yeni fonksiyonlarımızı bir kapanışa sarıyoruz.

def get_log_lik_transformed(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_transformed(transformed_precisions):
    return (log_lik_data_transformed(transformed_precisions, replicated_data) +
            log_lik_prior_transformed(transformed_precisions))

  return _log_lik_transformed

# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)

[-431.5611]

Örnekleme

Artık örnekleyicimizin geçersiz parametre değerleri nedeniyle patlaması konusunda endişelenmemize gerek olmadığına göre, bazı gerçek örnekler üretelim.

Örnekleyici, parametrelerimizin sınırlandırılmamış versiyonuyla çalışır, bu yüzden başlangıç ​​değerimizi kısıtlamasız versiyonuna dönüştürmemiz gerekir. Ürettiğimiz örneklerin tümü de kısıtlanmamış formlarında olacak, bu yüzden onları geri dönüştürmemiz gerekiyor. Bijektörler vektörleştirilmiştir, bu nedenle bunu yapmak kolaydır.

# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
    [[0.5 + np.random.uniform(), 0.0],
     [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
    dtype=np.float32)
initial_value =  initial_value_cholesky.dot(
  initial_value_cholesky.T)[np.newaxis, ...]

# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
  initial_value).numpy()

# Sample!
@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)

  num_results = 1000
  num_burnin_steps = 1000

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          initial_value_transformed,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=lambda _, pkr: pkr.is_accepted,
      seed=123)
  # transform samples back to their constrained form
  precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

Örnekleyicimizin çıktısının ortalamasını analitik sonsal ortalamayla karşılaştıralım!

print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Sample mean:
 [[ 1.4315274  -0.25587553]
 [-0.25587553  0.5740424 ]]

Çok uzaktayız! Nedenini bulalım. Önce örneklerimize bakalım.

np.reshape(precision_samples, [-1, 2, 2])

array([[[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       ...,

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]]], dtype=float32)

Uh oh - hepsi aynı değere sahip gibi görünüyor. Nedenini bulalım.

kernel_results_ değişken her eyalette en örnekleyicide hakkında bilgi verir adlandırılmış başlık olur. is_accepted alan anahtarı burada.

# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))

[False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False]
Fraction of samples accepted: 0.0

Tüm numunelerimiz reddedildi! Muhtemelen adım boyutumuz çok büyüktü. Seçilmek stepsize=0.1 tamamen keyfi.

Sürüm 3: uyarlanabilir adım boyutuyla örnekleme

Rastgele adım boyutu seçimim ile örnekleme başarısız olduğundan, birkaç gündem maddemiz var:

1. uyarlanabilir bir adım boyutu uygulamak ve
2. bazı yakınsama kontrolleri yapın.

Bazı güzel örnek kod yoktur tensorflow_probability/python/mcmc/hmc.py adaptif adım boyutları uygulanması için. Aşağıda uyarladım.

Ayrı var unutmayın sess.run() her adım için deyim. Bu, hata ayıklama için gerçekten yararlıdır, çünkü gerekirse adım başına bazı tanılamaları kolayca eklememize olanak tanır. Örneğin, artan ilerlemeyi, her adımın süresini vb. gösterebiliriz.

İpucu: örnekleme kadar karmaşa için bir görünüşe yaygın yolu döngü içinde grafik büyümesine sahip olmaktır. (Grafiğin oturum çalıştırılmadan önce sonlandırılmasının nedeni, tam da bu tür sorunları önlemektir.) Yine de finalize() kullanmıyorsanız, kodunuz yavaşlarsa yararlı bir hata ayıklama kontrolü grafiği yazdırmaktır. aracılığıyla her adımda boyutu len(mygraph.get_operations()) - uzunluk artarsa, muhtemelen bir şey feci yapıyoruz.

Burada 3 bağımsız zincir çalıştıracağız. Zincirler arasında bazı karşılaştırmalar yapmak, yakınsama olup olmadığını kontrol etmemize yardımcı olacaktır.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values = []
for i in range(N_CHAINS):
  initial_value_cholesky = np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32)
  initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)

initial_values_transformed = precision_to_unconstrained.forward(
  initial_values).numpy()

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=hmc,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values_transformed,
      kernel=adapted_kernel,
      trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
      parallel_iterations=1)
  # transform samples back to their constrained form
  precision_samples = precision_to_unconstrained.inverse(states)
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

Hızlı bir kontrol: Örneklememiz sırasındaki kabul oranımız 0,651 hedefimize yakındır.

print(np.mean(is_accepted))

0.6190666666666667

Daha da iyisi, örnek ortalamamız ve standart sapmamız analitik çözümden beklediğimize yakındır.

precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96426415 -1.6519215 ]
 [-1.6519215   3.8614824 ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13622096 0.25235635]
 [0.25235635 0.5394968 ]]

Yakınsama kontrolü

Genel olarak kontrol edecek bir analitik çözümümüz olmayacak, bu nedenle örnekleyicinin yakınsadığından emin olmamız gerekecek. Standart bir onay Gelman-Rubin olan \(\hat{R}\) çoklu örnekleme zincirleri gerektirir istatistik. \(\hat{R}\) önlemler derece zincirleri arasında hangi varyans (araçların) için zincirler aynı dağıtıldı eğer biri beklenebilecek olanın üzerindedir. Değerler \(\hat{R}\) 1'e yakın yaklaşık yakınlaşma belirtmek için kullanılır. Bkz kaynak detayları için.

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0038308 1.0005717]
 [1.0005717 1.0006068]]

Model eleştirisi

Analitik bir çözümümüz olmasaydı, gerçek bir model eleştirisi yapmanın tam zamanı olurdu.

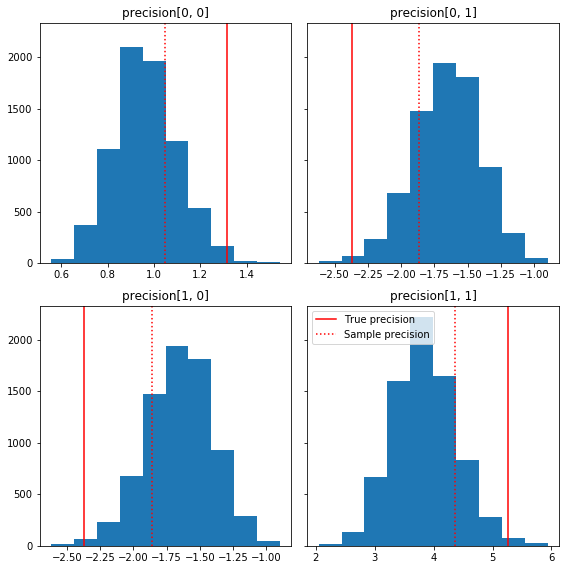
Burada temel gerçekliğimize göre örnek bileşenlerin birkaç hızlı histogramı verilmiştir (kırmızı). Numunelerin daha önce numune kesinlik matrisi değerlerinden kimlik matrisine doğru küçültüldüğüne dikkat edin.

fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    ax.hist(precision_samples_reshaped[:, i, j])
    ax.axvline(true_precision[i, j], color='red',
               label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':',
               label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()

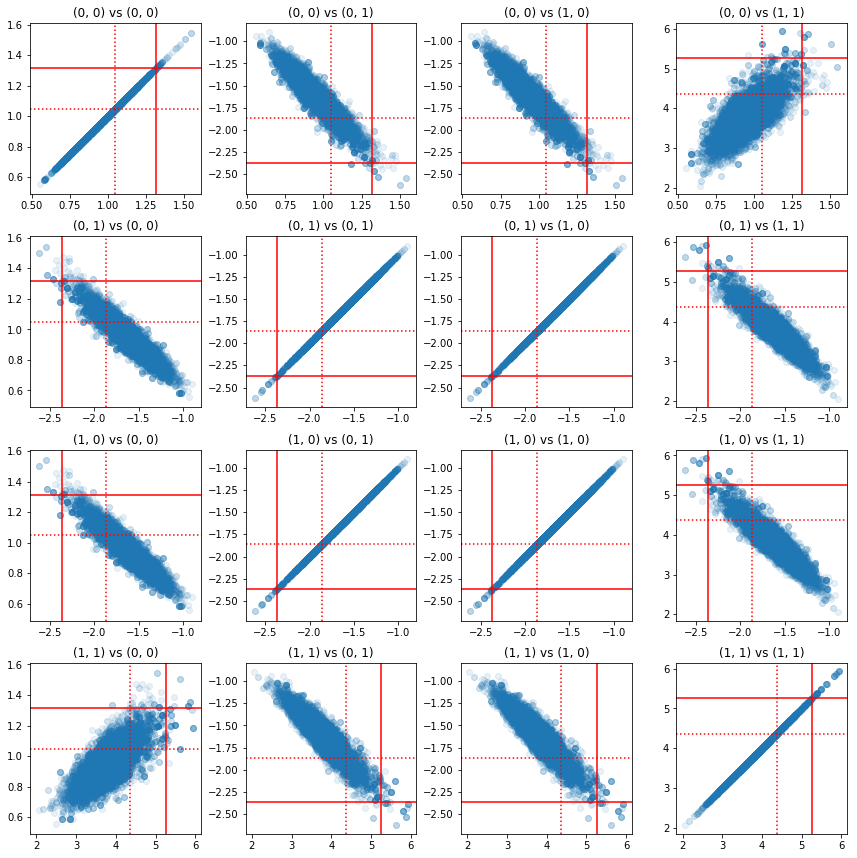
Hassas bileşen çiftlerinin bazı dağılım grafikleri, posteriorun korelasyon yapısı nedeniyle, gerçek posterior değerlerin yukarıdaki marjinallerden göründüğü kadar olası olmadığını göstermektedir.

fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
  for j1 in range(2):
    index1 = 2 * i1 + j1
    for i2 in range(2):
      for j2 in range(2):
        index2 = 2 * i2 + j2
        ax = axes[index1, index2]
        ax.scatter(precision_samples_reshaped[:, i1, j1],
                   precision_samples_reshaped[:, i2, j2], alpha=0.1)
        ax.axvline(true_precision[i1, j1], color='red')
        ax.axhline(true_precision[i2, j2], color='red')
        ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
        ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
        ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()

Sürüm 4: kısıtlı parametrelerin daha basit örneklemesi

Bijektörler, hassas matrisin örneklenmesini basit hale getirdi, ancak kısıtlamasız gösterime ve gösterimden makul miktarda manuel dönüştürme vardı. Daha kolay bir yol var!

TransformedTransitionKernel

TransformedTransitionKernel bu süreci kolaylaştırır. Örnekleyicinizi sarar ve tüm dönüşümleri yönetir. Argüman olarak, kısıtlanmamış parametre değerlerini kısıtlı olanlarla eşleştiren bir bijektör listesi alır. Yani burada biz tersini ihtiyacımız precision_to_unconstrained yukarıda kullandığımız bijector. Biz sadece kullanabilirsiniz tfb.Invert(precision_to_unconstrained) , ama bu terslerinin terslerinin alarak yer alacağı (TensorFlow basitleştirmek için akıllı yeterli değildir tf.Invert(tf.Invert()) için tf.Identity()) , bunun yerine biz Sadece yeni bir bijektör yazacağım.

kısıtlayıcı bijektör

# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
    # step 3: take the product of Cholesky factors
    tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: map a vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()

print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)

m:
 [[1.0, 2.0], [2.0, 8.0]]
unconstrained_to_precision.inverse(m):
 [0.6931472 2.        0.       ]
forward(unconstrained_to_precision.inverse(m)):
 [[1. 2.]
 [2. 8.]]

TransformedTransitionKernel ile Örnekleme

İle TransformedTransitionKernel , artık bizim parametrelerin manuel dönüşümleri yapmak zorundayız. Başlangıç ​​değerlerimiz ve örneklerimizin tümü hassas matrislerdir; sadece kısıtlayıcı olmayan bijektör(ler)imizi çekirdeğe aktarmamız gerekiyor ve tüm dönüşümleri o hallediyor.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  return states

precision_samples  = sample()

yakınsama kontrol ediliyor

\(\hat{R}\) yakınsama onay görünüyor iyi!

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013582 1.0019467]
 [1.0019467 1.0011805]]

Analitik posterior ile karşılaştırma

Tekrar analitik posteriora karşı kontrol edelim.

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96687526 -1.6552585 ]
 [-1.6552585   3.867676  ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329624 0.24913791]
 [0.24913791 0.53983927]]

optimizasyonlar

Artık uçtan uca çalışan işlerimiz olduğuna göre, daha optimize edilmiş bir sürüm yapalım. Bu örnek için hız çok önemli değil, ancak matrisler büyüdüğünde, birkaç optimizasyon büyük bir fark yaratacaktır.

Yapabileceğimiz büyük bir hız iyileştirmesi, Cholesky ayrıştırması açısından yeniden parametrelendirmektir. Bunun nedeni, veri olabilirlik fonksiyonumuzun hem kovaryans hem de kesinlik matrislerini gerektirmesidir. Ters matris pahalı (bir\(O(n^3)\) bir için \(n \times n\) matrisine) ve biz kovaryans veya hassas matrisinin ya açısından parameterize, biz diğer almak için bir ters çevirmeyi yapmak gerekmez.

Bir hatırlatma olarak, bir gerçek pozitif tanımlı, simetrik matris \(M\) şekilde bir ürün haline ayrıştırılabilir \(M = L L^T\) matris \(L\) alt üçgen biçimindedir ve pozitif diyagonalleri vardır. Arasında Choleskey çözümleme verilen \(M\), daha etkili bir şekilde elde edilebilmesi için \(M\) (daha düşük bir ürünü ve bir üst üçgen matris) ve \(M^{-1}\) (arka-ikamesi yoluyla). Cholesky çarpanlarına ayırmanın kendisinin hesaplanması ucuz değildir, ancak Cholesky faktörleri cinsinden parametreleştirirsek, yalnızca ilk parametre değerlerinin Choleksy çarpanlarına ayırmasını hesaplamamız gerekir.

Kovaryans matrisinin Cholesky ayrıştırmasını kullanma

TFP değişkenli normal dağılım, bir sürümü vardır MultivariateNormalTriL kovaryans matrisinin Cholesky faktörü açısından parametre belirlenmiştir. Dolayısıyla, kovaryans matrisinin Cholesky faktörü cinsinden parametreleştirecek olsaydık, veri günlüğü olasılığını verimli bir şekilde hesaplayabilirdik. Zorluk, önceki günlük olasılığını benzer verimlilikle hesaplamaktır.

Örneklerin Cholesky faktörleriyle çalışan ters Wishart dağılımının bir versiyonuna sahip olsaydık, her şey hazır olurdu. Ne yazık ki, yapmıyoruz. (Ekip kod gönderimlerini memnuniyetle karşılayacaktır!) Alternatif olarak, bir bijektör zinciri ile birlikte Cholesky örnek faktörleriyle çalışan Wishart dağıtımının bir sürümünü kullanabiliriz.

Şu anda, işleri gerçekten verimli hale getirmek için birkaç stok bijektörü kaçırıyoruz, ancak süreci bir alıştırma ve TFP'nin bijektörlerinin gücünün faydalı bir örneği olarak göstermek istiyorum.

Cholesky faktörleri üzerinde çalışan bir Wishart dağılımı

Wishart dağılımı, yararlı bir bayrağı vardır input_output_cholesky belirtir giriş ve çıkış matrisleri Cholesky faktörler olmalıdır ki. Cholesky faktörleriyle çalışmak tam matrislerden daha verimli ve sayısal olarak avantajlıdır, bu yüzden bu arzu edilir. Bayrak semantik ilgili önemli bir nokta: Bu dağıtımına giriş ve çıkış temsili değişmelidir belirten bir göstergedir - bu bir Jakobyan düzeltme yer alacağı dağıtım, tam bir reparameterization göstermez log_prob() işlev. Aslında bu tam yeniden parametrelendirmeyi yapmak istiyoruz, bu yüzden kendi dağıtımımızı oluşturacağız.

# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices.  Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).

class CholeskyWishart(tfd.TransformedDistribution):
  """Wishart distribution reparameterized to use Cholesky factors."""
  def __init__(self,
      df,
      scale_tril,
      validate_args=False,
      allow_nan_stats=True,
      name='CholeskyWishart'):
    # Wishart has a bunch of methods that we want to support but not
    # implement.  We'll subclass TransformedDistribution here to take care of
    # those.  We'll override the few for which speed is critical and implement
    # them with a separate Wishart for which input_output_cholesky=True
    super(CholeskyWishart, self).__init__(
        distribution=tfd.WishartTriL(
            df=df,
            scale_tril=scale_tril,
            input_output_cholesky=False,
            validate_args=validate_args,
            allow_nan_stats=allow_nan_stats),
        bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
        validate_args=validate_args,
        name=name
    )
    # Here's the Cholesky distribution we'll use for log_prob() and sample()
    self.cholesky = tfd.WishartTriL(
        df=df,
        scale_tril=scale_tril,
        input_output_cholesky=True,
        validate_args=validate_args,
        allow_nan_stats=allow_nan_stats)

  def _log_prob(self, x):
    return (self.cholesky.log_prob(x) +
            self.bijector.inverse_log_det_jacobian(x, event_ndims=2))

  def _sample_n(self, n, seed=None):
    return self.cholesky._sample_n(n, seed)

# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

@tf.function(autograph=False)
def compute_log_prob(m):
  w_transformed = tfd.TransformedDistribution(
      tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
      bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
  w_optimized = CholeskyWishart(
      df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
  log_prob_transformed = w_transformed.log_prob(m)
  log_prob_optimized = w_optimized.log_prob(m)
  return log_prob_transformed, log_prob_optimized

for matrix in [np.eye(2, dtype=np.float32),
               np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
  log_prob_transformed, log_prob_optimized = [
      t.numpy() for t in compute_log_prob(matrix)]
  print('Transformed Wishart:', log_prob_transformed)
  print('Optimized Wishart', log_prob_optimized)

Transformed Wishart: -0.84889317
Optimized Wishart -0.84889317
Transformed Wishart: -99.269455
Optimized Wishart -99.269455

Ters bir Wishart dağılımı oluşturma

Bizim kovaryans matrisi var \(C\) ayrılacak \(C = L L^T\) \(L\) alt üçgen ve olumlu çapını vardır. Biz olasılığını bilmek istiyorum \(L\) göz önüne alındığında \(C \sim W^{-1}(\nu, V)\) nerede \(W^{-1}\) Wishart dağılımı tersidir.

Ters Wishart dağılımı özelliğine sahip olduğu takdirde \(C \sim W^{-1}(\nu, V)\)ardından hassas matris \(C^{-1} \sim W(\nu, V^{-1})\). Bu yüzden olasılığını alabilirsiniz \(L\) bir aracılığı TransformedDistribution parametreleri olarak Wishart dağılımı ve onun tersi bir Choleskey faktörüne hassas matrisi Choleskey faktörünü eşleştiren bir bijector sürer.

Arasında Cholesky faktörü almak bir basit (ama süper verimli değildir) yolu \(C^{-1}\) için \(L\) daha sonra bu ters faktörlerden kovaryans matrisi oluşturan ve ardından Cholesky çarpanlara yapıyor, arka çözme tarafından Choleskey faktörünü ters etmektir .

Arasında Cholesky ayrışma edelim \(C^{-1} = M M^T\). \(M\) kullandığımız onu çevirin, böylece alt üçgen olduğunu MatrixInverseTriL bijector.

Şekillendirme \(C\) gelen \(M^{-1}\) : biraz zor \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) nedenle, daha düşük bir üçgen olan \(M^{-1}\) da daha düşük bir üçgen olacak ve \(M^{-T}\) üst üçgen olacaktır. CholeskyOuterProduct() biz oluşturmak için kullanamaz böylece bijector sadece alt üçgen matrisleri ile çalışır \(C\) gelen \(M^{-T}\). Çözümümüz, bir matrisin satırlarına ve sütunlarına izin veren bir kestiriciler zinciridir.

Neyse ki bu mantık içinde hapsedilmiştir CholeskyToInvCholesky bijector!

Tüm parçaları birleştirmek

# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()

print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)

numpy =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]
bijector =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]

Son dağıtımımız

Cholesky faktörleri üzerinde çalışan ters Wishart'ımız aşağıdaki gibidir:

inverse_wishart_cholesky = tfd.TransformedDistribution(
    distribution=CholeskyWishart(
        df=PRIOR_DF,
        scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
    bijector=tfb.CholeskyToInvCholesky())

Ters Wishart'ımız var, ancak bu biraz yavaş çünkü bijektörde bir Cholesky ayrıştırması yapmamız gerekiyor. Hassas matris parametreleştirmesine geri dönelim ve optimizasyon için orada neler yapabileceğimizi görelim.

Final(!) Versiyon: hassas matrisin Cholesky ayrıştırmasını kullanma

Alternatif bir yaklaşım, hassas matrisin Cholesky faktörleriyle çalışmaktır. Burada, önceki olabilirlik fonksiyonunun hesaplanması kolaydır, ancak veri günlüğü olabilirlik fonksiyonu, TFP'nin çok değişkenli normalin kesinlik ile parametrelenen bir versiyonuna sahip olmadığı için daha fazla iş gerektirir.

Optimize edilmiş önceki günlük olasılığı

Biz kullanmak CholeskyWishart biz önce inşa etmek yukarıda inşa dağılımı.

# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

def log_lik_prior_cholesky(precisions_cholesky):
  rv_precision = CholeskyWishart(
      df=PRIOR_DF,
      scale_tril=PRIOR_SCALE_CHOLESKY,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions_cholesky)

# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
              true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
    distribution=tfd.WishartTriL(
        df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
    bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
    precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
    precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow slow:', lik_tf_slow[i])
  print('tensorflow fast:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow slow: -0.84889317
tensorflow fast: -0.84889317
1
numpy: -7.442875031036973
tensorflow slow: -7.442877
tensorflow fast: -7.442876

Optimize edilmiş veri günlüğü olasılığı

We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:

Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)

Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)

Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.

Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now

\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)

So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).

Our approach (courtesy of this notebook ):

1. Use tfd.Independent() to combine a batch of 1-D Normal random variables into a single multi-dimensional random variable. The reinterpreted_batch_ndims parameter for Independent() specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, so reinterpreted_batch_ndims=1 .
2. Apply a bijector to add the desired covariance: tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)) . Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). The tfb.Invert takes care of inverting \(B\), and the adjoint=True flag performs the transpose.
3. Apply a bijector to add the desired offset: tfb.Shift(shift=shift) Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).

class MVNPrecisionCholesky(tfd.TransformedDistribution):
  """Multivariate normal parameterized by loc and Cholesky precision matrix."""

  def __init__(self, loc, precision_cholesky, name=None):
    super(MVNPrecisionCholesky, self).__init__(
        distribution=tfd.Independent(
            tfd.Normal(loc=tf.zeros_like(loc),
                       scale=tf.ones_like(loc)),
            reinterpreted_batch_ndims=1),
        bijector=tfb.Chain([
            tfb.Shift(shift=loc),
            tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
                                  adjoint=True)),
        ]),
        name=name)

@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
  n = tf.shape(precisions_cholesky)[0]  # number of precision matrices
  rv_data = MVNPrecisionCholesky(
      loc=tf.zeros([n, 2]),
      precision_cholesky=precisions_cholesky)
  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.81824

Combined log likelihood function

Now we combine our prior and data log likelihood functions in a closure.

def get_log_lik_cholesky(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_cholesky(precisions_cholesky):
    return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
            log_lik_prior_cholesky(precisions_cholesky))

  return _log_lik_cholesky

Constraining bijector

Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.

unconstrained_to_precision_cholesky = tfb.Chain([
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: expand the vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)

precisions_cholesky:
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

inv:
 [[ 0.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 3.5762781e-07 -2.0647411e+00  1.3721828e-01]]

fwd(inv):
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

Initial values

We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values_cholesky = []
for i in range(N_CHAINS):
  initial_values_cholesky.append(np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)

Sampling

We sample N_CHAINS chains using the TransformedTransitionKernel .

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_cholesky(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  samples = tf.linalg.matmul(states, states, transpose_b=True)
  return samples

precision_samples = sample()

Convergence check

A quick convergence check looks good:

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013583 1.0019467]
 [1.0019467 1.0011804]]

Comparing results to the analytic posterior

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])

And again, the sample means and standard deviations match those of the analytic posterior.

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.9668749 -1.6552604]
 [-1.6552604  3.8676758]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329637 0.24913797]
 [0.24913797 0.53983945]]

Ok, all done! We've got our optimized sampler working.