מורשה תחת רישיון MIT
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all
# copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
# SOFTWARE.
 הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
כדי להאט את התפשטות ה-COVID-19 בתחילת 2020, מדינות אירופה אימצו התערבויות לא פרמצבטיות כמו סגירת עסקים לא חיוניים, בידוד מקרים בודדים, איסורי נסיעה ואמצעים אחרים לעידוד התרחקות חברתית. אימפריאל קולג COVID-19 צוות התגובה נתח את היעילות של אמצעים אלה במאמרם "בהערכת מספר הזיהומים ואת ההשפעה של התערבויות שאינן תרופתיות על COVID-19 ב 11 מדינות באירופה" , באמצעות מודל היררכי בייס בשילוב עם המכניסטי מודל אפידמיולוגי.
Colab זה מכיל יישום TensorFlow Probability (TFP) של ניתוח זה, המאורגן באופן הבא:
- "הגדרת מודל" מגדירה את המודל האפידמיולוגי להעברת מחלות ומקרי מוות כתוצאה מכך, את ההתפלגות המוקדמת של בייסיאנית על פני פרמטרים של המודל, והתפלגות מספר מקרי המוות המותנים בערכי פרמטרים.
- "עיבוד מוקדם של נתונים" טוענת נתונים על עיתוי וסוג ההתערבויות בכל מדינה, ספירת מקרי מוות לאורך זמן ושיעורי מוות משוערים של הנדבקים.
- "הסקת מודל" בונה מודל היררכי בייסיאני ומריצה את המילטון מונטה קרלו (HMC) כדי לדגום מההתפלגות האחורית על פני פרמטרים.
- "תוצאות" מציגות התפלגות חזויה אחורית עבור כמויות עניין כגון מקרי מוות חזויים ומקרי מוות נגד עובדות בהיעדר התערבויות.
העיתון מצא ראיות כי מדינות הצליחו לצמצם את מספר הזיהומים החדשים המשודרים על ידי כול אדם נגוע (\(R_t\)), אבל זה במרווחים אמינים הכלול \(R_t=1\) (הערך שמעליו המגיפה ממשיכה להתפשט) ושזה מוקדם להסיק מסקנות נחרצות על יעילות ההתערבויות. קוד סטן עבור העיתון נמצא המחברים Github מאגר, ו Colab זה מתרבה 2 גרסה .
pip3 install -q git+git://github.com/arviz-devs/arviz.gitpip3 install -q tf-nightly tfp-nightly
יבוא
import collections
from pprint import pprint
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability.python.internal import prefer_static as ps
tf.enable_v2_behavior()
# Globally Enable XLA.
# tf.config.optimizer.set_jit(True)
try:
physical_devices = tf.config.list_physical_devices('GPU')
tf.config.experimental.set_memory_growth(physical_devices[0], True)
except:
# Invalid device or cannot modify virtual devices once initialized.
pass
tfb = tfp.bijectors
tfd = tfp.distributions
DTYPE = np.float32
1 הגדרת דגם
1.1 מודל מכני לזיהומים ומוות
מודל ההדבקה מדמה את מספר הזיהומים בכל מדינה לאורך זמן. נתוני קלט הם העיתוי וסוג ההתערבויות, גודל האוכלוסייה והמקרים הראשוניים. פרמטרים שולטים ביעילות ההתערבויות ובקצב העברת המחלה. המודל למספר הצפוי של מקרי מוות מיישם שיעור תמותה על הזיהומים החזויים.
מודל ההדבקה מבצע קונבולוציה של זיהומים יומיים קודמים עם התפלגות המרווחים הסדרתיים (ההתפלגות על פני מספר הימים בין ההידבקות להדבקה של מישהו אחר). בכל שלב בזמן, מספר זיהומים חדשים בשלב \(t\), \(n_t\), מחושבת
\begin{equation} \sum_{i=0}^{t-1} n_i \mu_t \text{p} (\text{נתפס ממישהו שנדבק ב-} i | \text{נדבק לאחרונה ב-} t) \end{ משוואת} איפה \(\mu_t=R_t\) ואת ההסתברות המותנה מאוחסנת conv_serial_interval , כהגדרתו להלן.
המודל למקרי מוות צפויים מבצע קונבולוציה של זיהומים יומיומיים וחלוקת הימים בין זיהום למוות. כלומר, מותם צפוי ביום \(t\) מחושב
\ להתחיל {משוואה} \ sum_ {i = 0} ^ {t-1} n_i \ הטקסט {p (מוות ביום \(t\)| זיהום ביום \(i\))} \ end {המשוואה} שבו הסתברות מותנה מאוחסן ב conv_fatality_rate , כהגדרתו להלן.
from tensorflow_probability.python.internal import broadcast_util as bu
def predict_infections(
intervention_indicators, population, initial_cases, mu, alpha_hier,
conv_serial_interval, initial_days, total_days):
"""Predict the number of infections by forward-simulation.
Args:
intervention_indicators: Binary array of shape
`[num_countries, total_days, num_interventions]`, in which `1` indicates
the intervention is active in that country at that time and `0` indicates
otherwise.
population: Vector of length `num_countries`. Population of each country.
initial_cases: Array of shape `[batch_size, num_countries]`. Number of cases
in each country at the start of the simulation.
mu: Array of shape `[batch_size, num_countries]`. Initial reproduction rate
(R_0) by country.
alpha_hier: Array of shape `[batch_size, num_interventions]` representing
the effectiveness of interventions.
conv_serial_interval: Array of shape
`[total_days - initial_days, total_days]` output from
`make_conv_serial_interval`. Convolution kernel for serial interval
distribution.
initial_days: Integer, number of sequential days to seed infections after
the 10th death in a country. (N0 in the authors' Stan code.)
total_days: Integer, number of days of observed data plus days to forecast.
(N2 in the authors' Stan code.)
Returns:
predicted_infections: Array of shape
`[total_days, batch_size, num_countries]`. (Batched) predicted number of
infections over time and by country.
"""
alpha = alpha_hier - tf.cast(np.log(1.05) / 6.0, DTYPE)
# Multiply the effectiveness of each intervention in each country (alpha)
# by the indicator variable for whether the intervention was active and sum
# over interventions, yielding an array of shape
# [total_days, batch_size, num_countries] that represents the total effectiveness of
# all interventions in each country on each day (for a batch of data).
linear_prediction = tf.einsum(
'ijk,...k->j...i', intervention_indicators, alpha)
# Adjust the reproduction rate per country downward, according to the
# effectiveness of the interventions.
rt = mu * tf.exp(-linear_prediction, name='reproduction_rate')
# Initialize storage array for daily infections and seed it with initial
# cases.
daily_infections = tf.TensorArray(
dtype=DTYPE, size=total_days, element_shape=initial_cases.shape)
for i in range(initial_days):
daily_infections = daily_infections.write(i, initial_cases)
# Initialize cumulative cases.
init_cumulative_infections = initial_cases * initial_days
# Simulate forward for total_days days.
cond = lambda i, *_: i < total_days
def body(i, prev_daily_infections, prev_cumulative_infections):
# The probability distribution over days j that someone infected on day i
# caught the virus from someone infected on day j.
p_infected_on_day = tf.gather(
conv_serial_interval, i - initial_days, axis=0)
# Multiply p_infected_on_day by the number previous infections each day and
# by mu, and sum to obtain new infections on day i. Mu is adjusted by
# the fraction of the population already infected, so that the population
# size is the upper limit on the number of infections.
prev_daily_infections_array = prev_daily_infections.stack()
to_sum = prev_daily_infections_array * bu.left_justified_expand_dims_like(
p_infected_on_day, prev_daily_infections_array)
convolution = tf.reduce_sum(to_sum, axis=0)
rt_adj = (
(population - prev_cumulative_infections) / population
) * tf.gather(rt, i)
new_infections = rt_adj * convolution
# Update the prediction array and the cumulative number of infections.
daily_infections = prev_daily_infections.write(i, new_infections)
cumulative_infections = prev_cumulative_infections + new_infections
return i + 1, daily_infections, cumulative_infections
_, daily_infections_final, last_cumm_sum = tf.while_loop(
cond, body,
(initial_days, daily_infections, init_cumulative_infections),
maximum_iterations=(total_days - initial_days))
return daily_infections_final.stack()
def predict_deaths(predicted_infections, ifr_noise, conv_fatality_rate):
"""Expected number of reported deaths by country, by day.
Args:
predicted_infections: Array of shape
`[total_days, batch_size, num_countries]` output from
`predict_infections`.
ifr_noise: Array of shape `[batch_size, num_countries]`. Noise in Infection
Fatality Rate (IFR).
conv_fatality_rate: Array of shape
`[total_days - 1, total_days, num_countries]`. Convolutional kernel for
calculating fatalities, output from `make_conv_fatality_rate`.
Returns:
predicted_deaths: Array of shape `[total_days, batch_size, num_countries]`.
(Batched) predicted number of deaths over time and by country.
"""
# Multiply the number of infections on day j by the probability of death
# on day i given infection on day j, and sum over j. This yields the expected
result_remainder = tf.einsum(
'i...j,kij->k...j', predicted_infections, conv_fatality_rate) * ifr_noise
# Concatenate the result with a vector of zeros so that the first day is
# included.
result_temp = 1e-15 * predicted_infections[:1]
return tf.concat([result_temp, result_remainder], axis=0)
1.2 ערכי פרמטרים קודמים
כאן אנו מגדירים את ההתפלגות הקודמת המשותפת על פני פרמטרי המודל. ההנחה היא שרבים מערכי הפרמטרים הם בלתי תלויים, כך שניתן לבטא את הקודקוד כ:
\(\text p(\tau, y, \psi, \kappa, \mu, \alpha) = \text p(\tau)\text p(y|\tau)\text p(\psi)\text p(\kappa)\text p(\mu|\kappa)\text p(\alpha)\text p(\epsilon)\)
שבו:
- \(\tau\) הוא פרמטר השיעור המשותף של ההתפלגות המעריכית על מספר המקרים הראשוניים לכול ארץ, \(y = y_1, ... y_{\text{num_countries} }\).
- \(\psi\) הוא פרמטר ב בהתפלגות בינומית שלילית עבור מספר מקרי המוות.
- \(\kappa\) הוא פרמטר מידה המשותף של חלוק HalfNormal על מספר הרבייה הראשוני בכול מדינה, \(\mu = \mu_1, ..., \mu_{\text{num_countries} }\) (המציין את מספר מקרים נוספים המשודרים על ידי כול אדם נגוע).
- \(\alpha = \alpha_1, ..., \alpha_6\) הוא האפקטיבי של כול אחד משש ההתערבויות.
- \(\epsilon\) (שנקרא
ifr_noiseבקוד, לאחר קוד סטן מחברים) הוא רעש זיהום לתמותה (IFR).
אנו מבטאים מודל זה כ-TFP JointDistribution, סוג של הפצת TFP המאפשרת ביטוי של מודלים גרפיים הסתברותיים.
def make_jd_prior(num_countries, num_interventions):
return tfd.JointDistributionSequentialAutoBatched([
# Rate parameter for the distribution of initial cases (tau).
tfd.Exponential(rate=tf.cast(0.03, DTYPE)),
# Initial cases for each country.
lambda tau: tfd.Sample(
tfd.Exponential(rate=tf.cast(1, DTYPE) / tau),
sample_shape=num_countries),
# Parameter in Negative Binomial model for deaths (psi).
tfd.HalfNormal(scale=tf.cast(5, DTYPE)),
# Parameter in the distribution over the initial reproduction number, R_0
# (kappa).
tfd.HalfNormal(scale=tf.cast(0.5, DTYPE)),
# Initial reproduction number, R_0, for each country (mu).
lambda kappa: tfd.Sample(
tfd.TruncatedNormal(loc=3.28, scale=kappa, low=1e-5, high=1e5),
sample_shape=num_countries),
# Impact of interventions (alpha; shared for all countries).
tfd.Sample(
tfd.Gamma(tf.cast(0.1667, DTYPE), 1), sample_shape=num_interventions),
# Multiplicative noise in Infection Fatality Rate.
tfd.Sample(
tfd.TruncatedNormal(
loc=tf.cast(1., DTYPE), scale=0.1, low=1e-5, high=1e5),
sample_shape=num_countries)
])
1.3 סבירות למקרי מוות שנצפו מותנה בערכי פרמטרים
האקספרס מודל הסבירות \(p(\text{deaths} | \tau, y, \psi, \kappa, \mu, \alpha, \epsilon)\). הוא מיישם את המודלים למספר הזיהומים ומקרי המוות הצפויים המותנים בפרמטרים, ומניח שהמוות בפועל עוקב אחר התפלגות בינומית שלילית.
def make_likelihood_fn(
intervention_indicators, population, deaths,
infection_fatality_rate, initial_days, total_days):
# Create a mask for the initial days of simulated data, as they are not
# counted in the likelihood.
observed_deaths = tf.constant(deaths.T[np.newaxis, ...], dtype=DTYPE)
mask_temp = deaths != -1
mask_temp[:, :START_DAYS] = False
observed_deaths_mask = tf.constant(mask_temp.T[np.newaxis, ...])
conv_serial_interval = make_conv_serial_interval(initial_days, total_days)
conv_fatality_rate = make_conv_fatality_rate(
infection_fatality_rate, total_days)
def likelihood_fn(tau, initial_cases, psi, kappa, mu, alpha_hier, ifr_noise):
# Run models for infections and expected deaths
predicted_infections = predict_infections(
intervention_indicators, population, initial_cases, mu, alpha_hier,
conv_serial_interval, initial_days, total_days)
e_deaths_all_countries = predict_deaths(
predicted_infections, ifr_noise, conv_fatality_rate)
# Construct the Negative Binomial distribution for deaths by country.
mu_m = tf.transpose(e_deaths_all_countries, [1, 0, 2])
psi_m = psi[..., tf.newaxis, tf.newaxis]
probs = tf.clip_by_value(mu_m / (mu_m + psi_m), 1e-9, 1.)
likelihood_elementwise = tfd.NegativeBinomial(
total_count=psi_m, probs=probs).log_prob(observed_deaths)
return tf.reduce_sum(
tf.where(observed_deaths_mask,
likelihood_elementwise,
tf.zeros_like(likelihood_elementwise)),
axis=[-2, -1])
return likelihood_fn
1.4 הסתברות למוות בהינתן זיהום
חלק זה מחשב את התפלגות מקרי המוות בימים שלאחר ההדבקה. זה מניח שהזמן מההדבקה למוות הוא סכום של שתי כמויות משתנות גמא, המייצגות את הזמן מההדבקה להופעת המחלה ואת הזמן מההתחלה למוות. השעה-אל-מוות הפצה בשילוב עם נתוני זיהום לתמותה מן וריטי ואח. (2020) כדי לחשב את ההסתברות של מוות בימים הבאים זיהום.
def daily_fatality_probability(infection_fatality_rate, total_days):
"""Computes the probability of death `d` days after infection."""
# Convert from alternative Gamma parametrization and construct distributions
# for number of days from infection to onset and onset to death.
concentration1 = tf.cast((1. / 0.86)**2, DTYPE)
rate1 = concentration1 / 5.1
concentration2 = tf.cast((1. / 0.45)**2, DTYPE)
rate2 = concentration2 / 18.8
infection_to_onset = tfd.Gamma(concentration=concentration1, rate=rate1)
onset_to_death = tfd.Gamma(concentration=concentration2, rate=rate2)
# Create empirical distribution for number of days from infection to death.
inf_to_death_dist = tfd.Empirical(
infection_to_onset.sample([5e6]) + onset_to_death.sample([5e6]))
# Subtract the CDF value at day i from the value at day i + 1 to compute the
# probability of death on day i given infection on day 0, and given that
# death (not recovery) is the outcome.
times = np.arange(total_days + 1., dtype=DTYPE) + 0.5
cdf = inf_to_death_dist.cdf(times).numpy()
f_before_ifr = cdf[1:] - cdf[:-1]
# Explicitly set the zeroth value to the empirical cdf at time 1.5, to include
# the mass between time 0 and time .5.
f_before_ifr[0] = cdf[1]
# Multiply the daily fatality rates conditional on infection and eventual
# death (f_before_ifr) by the infection fatality rates (probability of death
# given intection) to obtain the probability of death on day i conditional
# on infection on day 0.
return infection_fatality_rate[..., np.newaxis] * f_before_ifr
def make_conv_fatality_rate(infection_fatality_rate, total_days):
"""Computes the probability of death on day `i` given infection on day `j`."""
p_fatal_all_countries = daily_fatality_probability(
infection_fatality_rate, total_days)
# Use the probability of death d days after infection in each country
# to build an array of shape [total_days - 1, total_days, num_countries],
# where the element [i, j, c] is the probability of death on day i+1 given
# infection on day j in country c.
conv_fatality_rate = np.zeros(
[total_days - 1, total_days, p_fatal_all_countries.shape[0]])
for n in range(1, total_days):
conv_fatality_rate[n - 1, 0:n, :] = (
p_fatal_all_countries[:, n - 1::-1]).T
return tf.constant(conv_fatality_rate, dtype=DTYPE)
1.5 מרווח סדרתי
המרווח הסדרתי הוא הזמן בין מקרים עוקבים בשרשרת של העברת מחלות, ויש להניח שהוא מופץ גמא. אנו משתמשים חלוקת המרווח סדרתי כדי לחשב את ההסתברות שאדם נדבק ביום \(i\) נדבק בווירוס מאדם נגוע בעבר ביום \(j\) (את conv_serial_interval טיעון כדי predict_infections ).
def make_conv_serial_interval(initial_days, total_days):
"""Construct the convolutional kernel for infection timing."""
g = tfd.Gamma(tf.cast(1. / (0.62**2), DTYPE), 1./(6.5*0.62**2))
g_cdf = g.cdf(np.arange(total_days, dtype=DTYPE))
# Approximate the probability mass function for the number of days between
# successive infections.
serial_interval = g_cdf[1:] - g_cdf[:-1]
# `conv_serial_interval` is an array of shape
# [total_days - initial_days, total_days] in which entry [i, j] contains the
# probability that an individual infected on day i + initial_days caught the
# virus from someone infected on day j.
conv_serial_interval = np.zeros([total_days - initial_days, total_days])
for n in range(initial_days, total_days):
conv_serial_interval[n - initial_days, 0:n] = serial_interval[n - 1::-1]
return tf.constant(conv_serial_interval, dtype=DTYPE)
2 עיבוד נתונים מראש
COUNTRIES = [
'Austria',
'Belgium',
'Denmark',
'France',
'Germany',
'Italy',
'Norway',
'Spain',
'Sweden',
'Switzerland',
'United_Kingdom'
]
2.1 אחזור ועיבוד מוקדם של נתוני התערבויות
raw_interventions = pd.read_csv(
'https://raw.githubusercontent.com/ImperialCollegeLondon/covid19model/master/data/interventions.csv')
raw_interventions['Date effective'] = pd.to_datetime(
raw_interventions['Date effective'], dayfirst=True)
interventions = raw_interventions.pivot(index='Country', columns='Type', values='Date effective')
# If any interventions happened after the lockdown, use the date of the lockdown.
for col in interventions.columns:
idx = interventions[col] > interventions['Lockdown']
interventions.loc[idx, col] = interventions[idx]['Lockdown']
num_countries = len(COUNTRIES)
2.2 אחזר נתוני מקרה/מוות והצטרף להתערבויות
# Load the case data
data = pd.read_csv('https://raw.githubusercontent.com/ImperialCollegeLondon/covid19model/master/data/COVID-19-up-to-date.csv')
# You can also use the dataset directly from european cdc (where the ICL model fetch their data from)
# data = pd.read_csv('https://opendata.ecdc.europa.eu/covid19/casedistribution/csv')
data['country'] = data['countriesAndTerritories']
data = data[['dateRep', 'cases', 'deaths', 'country']]
data = data[data['country'].isin(COUNTRIES)]
data['dateRep'] = pd.to_datetime(data['dateRep'], format='%d/%m/%Y')
# Add 0/1 features for whether or not each intevention was in place.
data = data.join(interventions, on='country', how='outer')
for col in interventions.columns:
data[col] = (data['dateRep'] >= data[col]).astype(int)
# Add "any_intevention" 0/1 feature.
any_intervention_list = ['Schools + Universities',
'Self-isolating if ill',
'Public events',
'Lockdown',
'Social distancing encouraged']
data['any_intervention'] = (
data[any_intervention_list].apply(np.sum, 'columns') > 0).astype(int)
# Index by country and date.
data = data.sort_values(by=['country', 'dateRep'])
data = data.set_index(['country', 'dateRep'])
2.3 אחזור ועיבוד נתוני אוכלוסייה נדבקים ונתוני מוות
infected_fatality_ratio = pd.read_csv(
'https://raw.githubusercontent.com/ImperialCollegeLondon/covid19model/master/data/popt_ifr.csv')
infected_fatality_ratio = infected_fatality_ratio.replace(to_replace='United Kingdom', value='United_Kingdom')
infected_fatality_ratio['Country'] = infected_fatality_ratio.iloc[:, 1]
infected_fatality_ratio = infected_fatality_ratio[infected_fatality_ratio['Country'].isin(COUNTRIES)]
infected_fatality_ratio = infected_fatality_ratio[
['Country', 'popt', 'ifr']].set_index('Country')
infected_fatality_ratio = infected_fatality_ratio.sort_index()
infection_fatality_rate = infected_fatality_ratio['ifr'].to_numpy()
population_value = infected_fatality_ratio['popt'].to_numpy()
2.4 עיבוד מוקדם של נתונים ספציפיים למדינה
# Model up to 75 days of data for each country, starting 30 days before the
# tenth cumulative death.
START_DAYS = 30
MAX_DAYS = 102
COVARIATE_COLUMNS = any_intervention_list + ['any_intervention']
# Initialize an array for number of deaths.
deaths = -np.ones((num_countries, MAX_DAYS), dtype=DTYPE)
# Assuming every intervention is still inplace in the unobserved future
num_interventions = len(COVARIATE_COLUMNS)
intervention_indicators = np.ones((num_countries, MAX_DAYS, num_interventions))
first_days = {}
for i, c in enumerate(COUNTRIES):
c_data = data.loc[c]
# Include data only after 10th death in a country.
mask = c_data['deaths'].cumsum() >= 10
# Get the date that the epidemic starts in a country.
first_day = c_data.index[mask][0] - pd.to_timedelta(START_DAYS, 'days')
c_data = c_data.truncate(before=first_day)
# Truncate the data after 28 March 2020 for comparison with Flaxman et al.
c_data = c_data.truncate(after='2020-03-28')
c_data = c_data.iloc[:MAX_DAYS]
days_of_data = c_data.shape[0]
deaths[i, :days_of_data] = c_data['deaths']
intervention_indicators[i, :days_of_data] = c_data[
COVARIATE_COLUMNS].to_numpy()
first_days[c] = first_day
# Number of sequential days to seed infections after the 10th death in a
# country. (N0 in authors' Stan code.)
INITIAL_DAYS = 6
# Number of days of observed data plus days to forecast. (N2 in authors' Stan
# code.)
TOTAL_DAYS = deaths.shape[1]
3 מסקנות דגם
Flaxman et al. (2020) השתמש סטן כדי מדגם מן אחורי פרמטר עם המילטוניאן מונטה קרלו (HMC) ואת הדגם לא-U-Turn (האגוזים).
כאן, אנו מיישמים את HMC עם התאמת גודל צעדים בממוצע כפול. אנו משתמשים בהרצת פיילוט של HMC לצורך התניה מוקדמת ואיתחול.
ההסקה פועלת תוך מספר דקות על GPU.
3.1 בניית מוקדם והסבירות עבור המודל
jd_prior = make_jd_prior(num_countries, num_interventions)
likelihood_fn = make_likelihood_fn(
intervention_indicators, population_value, deaths,
infection_fatality_rate, INITIAL_DAYS, TOTAL_DAYS)
3.2 כלי עזר
def get_bijectors_from_samples(samples, unconstraining_bijectors, batch_axes):
"""Fit bijectors to the samples of a distribution.
This fits a diagonal covariance multivariate Gaussian transformed by the
`unconstraining_bijectors` to the provided samples. The resultant
transformation can be used to precondition MCMC and other inference methods.
"""
state_std = [
tf.math.reduce_std(bij.inverse(x), axis=batch_axes)
for x, bij in zip(samples, unconstraining_bijectors)
]
state_mu = [
tf.math.reduce_mean(bij.inverse(x), axis=batch_axes)
for x, bij in zip(samples, unconstraining_bijectors)
]
return [tfb.Chain([cb, tfb.Shift(sh), tfb.Scale(sc)])
for cb, sh, sc in zip(unconstraining_bijectors, state_mu, state_std)]
def generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors):
"""Creates an initial MCMC state, and bijectors from the prior."""
prior_samples = jd_prior.sample(4096)
bijectors = get_bijectors_from_samples(
prior_samples, unconstraining_bijectors, batch_axes=0)
init_state = [
bij(tf.zeros([nchain] + list(s), DTYPE))
for s, bij in zip(jd_prior.event_shape, bijectors)
]
return init_state, bijectors
@tf.function(autograph=False, experimental_compile=True)
def sample_hmc(
init_state,
step_size,
target_log_prob_fn,
unconstraining_bijectors,
num_steps=500,
burnin=50,
num_leapfrog_steps=10):
def trace_fn(_, pkr):
return {
'target_log_prob': pkr.inner_results.inner_results.accepted_results.target_log_prob,
'diverging': ~(pkr.inner_results.inner_results.log_accept_ratio > -1000.),
'is_accepted': pkr.inner_results.inner_results.is_accepted,
'step_size': [tf.exp(s) for s in pkr.log_averaging_step],
}
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn,
step_size=step_size,
num_leapfrog_steps=num_leapfrog_steps)
hmc = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc,
bijector=unconstraining_bijectors)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(burnin * 0.8),
target_accept_prob=0.8,
decay_rate=0.5)
# Sampling from the chain.
return tfp.mcmc.sample_chain(
num_results=burnin + num_steps,
current_state=init_state,
kernel=hmc,
trace_fn=trace_fn)
3.3 הגדירו מכנסי חללי אירועים
HMC היא יעילה ביותר כאשר דגימה מתוך התפלגות גאוסיאנית מרובה משתנית איזוטרופיים ( Mangoubi & Smith (2017) ), ולכן הצעד הראשון הוא התנאי מוקדם צפיפות יעד המראה עד כמה כאלה ככל האפשר.
בראש ובראשונה, אנו הופכים משתנים מוגבלים (למשל, לא שליליים) למרחב לא מוגבל, מה ש-HMC דורש. בנוסף, אנו מעסיקים את ה-SinhArcsinh-bijector כדי לתמרן את הכבדות של זנבות צפיפות המטרה שעברה שינוי; אנחנו רוצים אלה ליפול בערך כמו \(e^{-x^2}\).
unconstraining_bijectors = [
tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # tau
tfb.Chain([tfb.Scale(tf.constant(1 / 0.03, DTYPE)), tfb.Softplus(),
tfb.SinhArcsinh(tailweight=tf.constant(1.85, DTYPE))]), # initial_cases
tfb.Softplus(), # psi
tfb.Softplus(), # kappa
tfb.Softplus(), # mu
tfb.Chain([tfb.Scale(tf.constant(0.4, DTYPE)), tfb.Softplus(),
tfb.SinhArcsinh(skewness=tf.constant(-0.2, DTYPE), tailweight=tf.constant(2., DTYPE))]), # alpha
tfb.Softplus(), # ifr_noise
]
ריצת פיילוט 3.4 HMC
אנו מפעילים תחילה את HMC המותנה מראש על ידי הקודמת, מאותחל מ-0 במרחב שעבר טרנספורמציה. אנחנו לא משתמשים בדגימות הקודמות כדי לאתחל את השרשרת, מכיוון שבפועל אלו גורמות לרוב לשרשראות תקועות בגלל מספרים לקויים.
%%time
nchain = 32
target_log_prob_fn = lambda *x: jd_prior.log_prob(*x) + likelihood_fn(*x)
init_state, bijectors = generate_init_state_and_bijectors_from_prior(nchain, unconstraining_bijectors)
# Each chain gets its own step size.
step_size = [tf.fill([nchain] + [1] * (len(s.shape) - 1), tf.constant(0.01, DTYPE)) for s in init_state]
burnin = 200
num_steps = 100
pilot_samples, pilot_sampler_stat = sample_hmc(
init_state,
step_size,
target_log_prob_fn,
bijectors,
num_steps=num_steps,
burnin=burnin,
num_leapfrog_steps=10)
CPU times: user 56.8 s, sys: 2.34 s, total: 59.1 s Wall time: 1min 1s
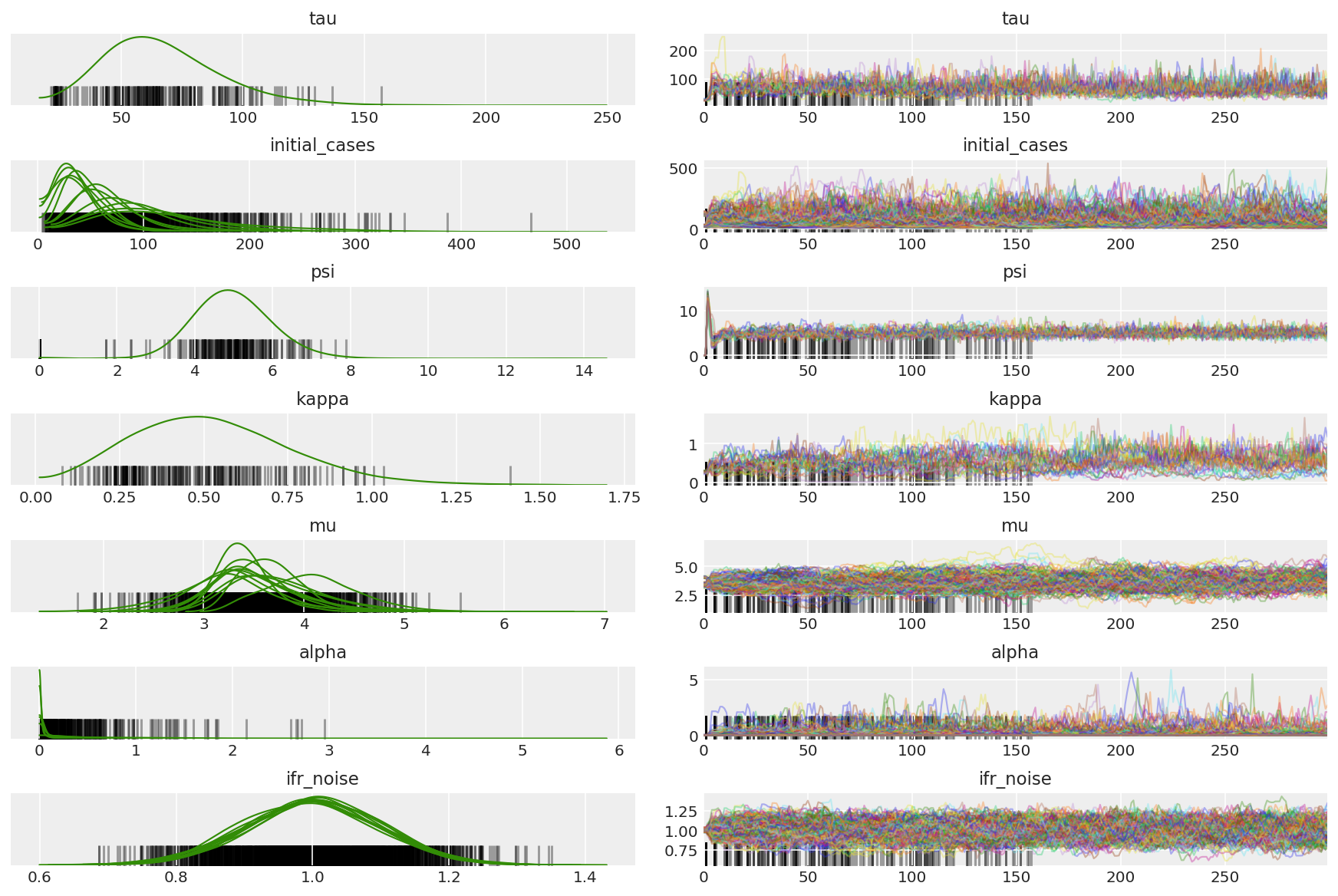
3.5 דמיינו דגימות פיילוט
אנחנו מחפשים שרשראות תקועות והתכנסות מעוררת עיניים. אנחנו יכולים לעשות כאן אבחון רשמי, אבל זה לא הכרחי בהתחשב בעובדה שזו רק ריצת פיילוט.
import arviz as az
az.style.use('arviz-darkgrid')
var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']
pilot_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, pilot_samples)}
אנו רואים הבדלים במהלך החימום, בעיקר בגלל שהתאמת גודל הצעד הממוצעת כפולה משתמשת בחיפוש אגרסיבי מאוד אחר גודל הצעד האופטימלי. ברגע שההסתגלות נכבית, גם הפערים נעלמים.
az_trace = az.from_dict(posterior=pilot_with_warmup,
sample_stats={'diverging': np.swapaxes(pilot_sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));
plt.plot(pilot_sampler_stat['step_size'][0]);
3.6 הפעל את HMC
באופן עקרוני נוכל להשתמש בדגימות הפיילוט לניתוח סופי (אם נריץ אותו לזמן ארוך יותר כדי לקבל התכנסות), אבל זה קצת יותר יעיל להתחיל ריצת HMC נוספת, הפעם מותנית מראש ואותחלה על ידי דגימות פיילוט.
%%time
burnin = 50
num_steps = 200
bijectors = get_bijectors_from_samples([s[burnin:] for s in pilot_samples],
unconstraining_bijectors=unconstraining_bijectors,
batch_axes=(0, 1))
samples, sampler_stat = sample_hmc(
[s[-1] for s in pilot_samples],
[s[-1] for s in pilot_sampler_stat['step_size']],
target_log_prob_fn,
bijectors,
num_steps=num_steps,
burnin=burnin,
num_leapfrog_steps=20)
CPU times: user 1min 26s, sys: 3.88 s, total: 1min 30s Wall time: 1min 32s
plt.plot(sampler_stat['step_size'][0]);
3.7 הדמיית דוגמאות
import arviz as az
az.style.use('arviz-darkgrid')
var_name = ['tau', 'initial_cases', 'psi', 'kappa', 'mu', 'alpha', 'ifr_noise']
posterior = {k: np.swapaxes(v.numpy()[burnin:], 1, 0)
for k, v in zip(var_name, samples)}
posterior_with_warmup = {k: np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
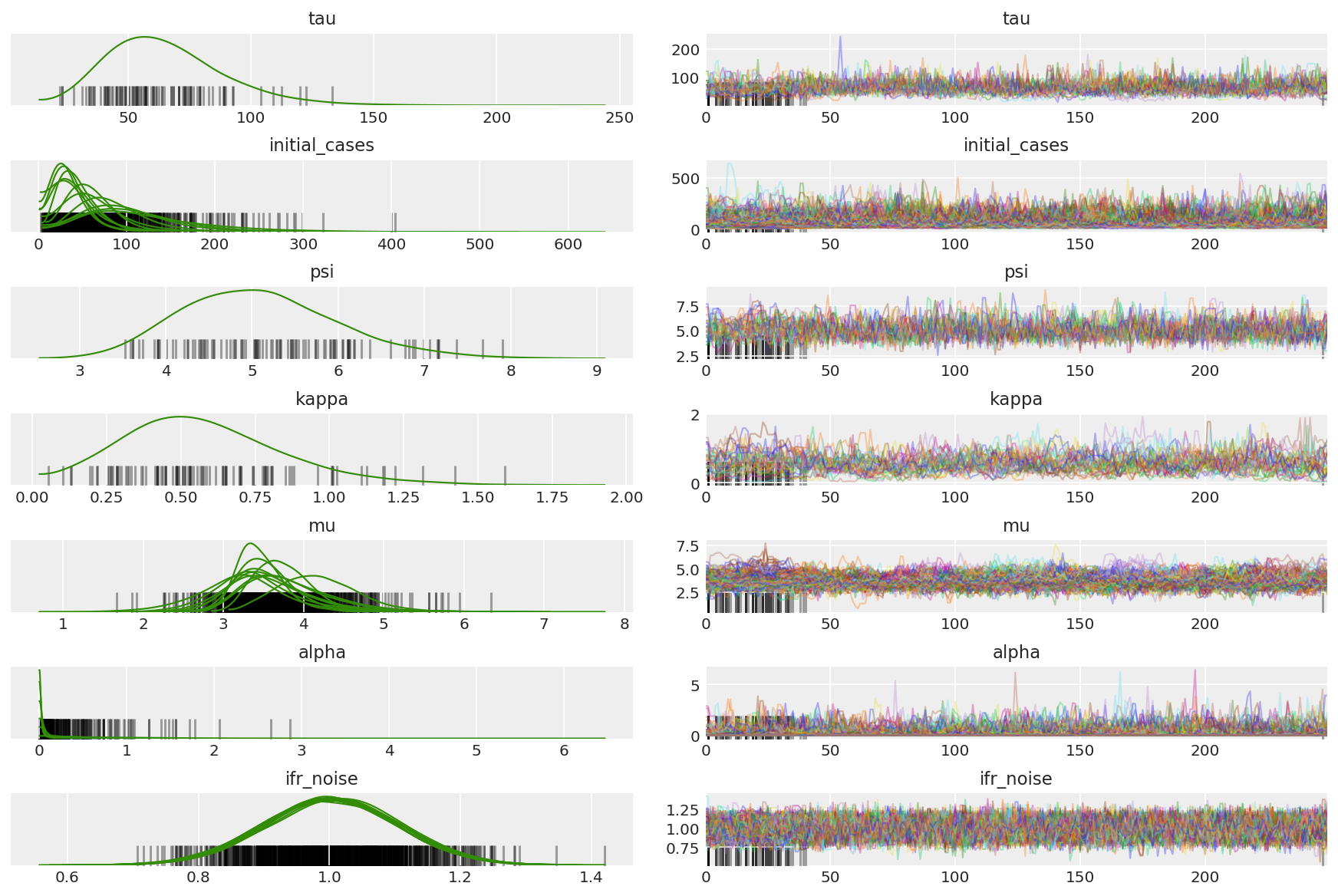
חשב את סיכום השרשראות. אנחנו מחפשים ESS גבוה ו-r_hat קרוב ל-1.
az.summary(posterior)
az_trace = az.from_dict(posterior=posterior_with_warmup,
sample_stats={'diverging': np.swapaxes(sampler_stat['diverging'].numpy(), 0, 1)})
az.plot_trace(az_trace, combined=True, compact=True, figsize=(12, 8));
זה מאלף להסתכל על פונקציות המתאם האוטומטי בכל הממדים. אנחנו מחפשים פונקציות שיורדות מהר, אבל לא עד כדי כך שהן נכנסות לשלילה (מה שמעיד על כך ש-HMC פוגע בתהודה, וזה רע לארגודיסטיות ויכול להכניס הטיה).
with az.rc_context(rc={'plot.max_subplots': None}):
az.plot_autocorr(posterior, combined=True, figsize=(12, 16), textsize=12);

4 תוצאות
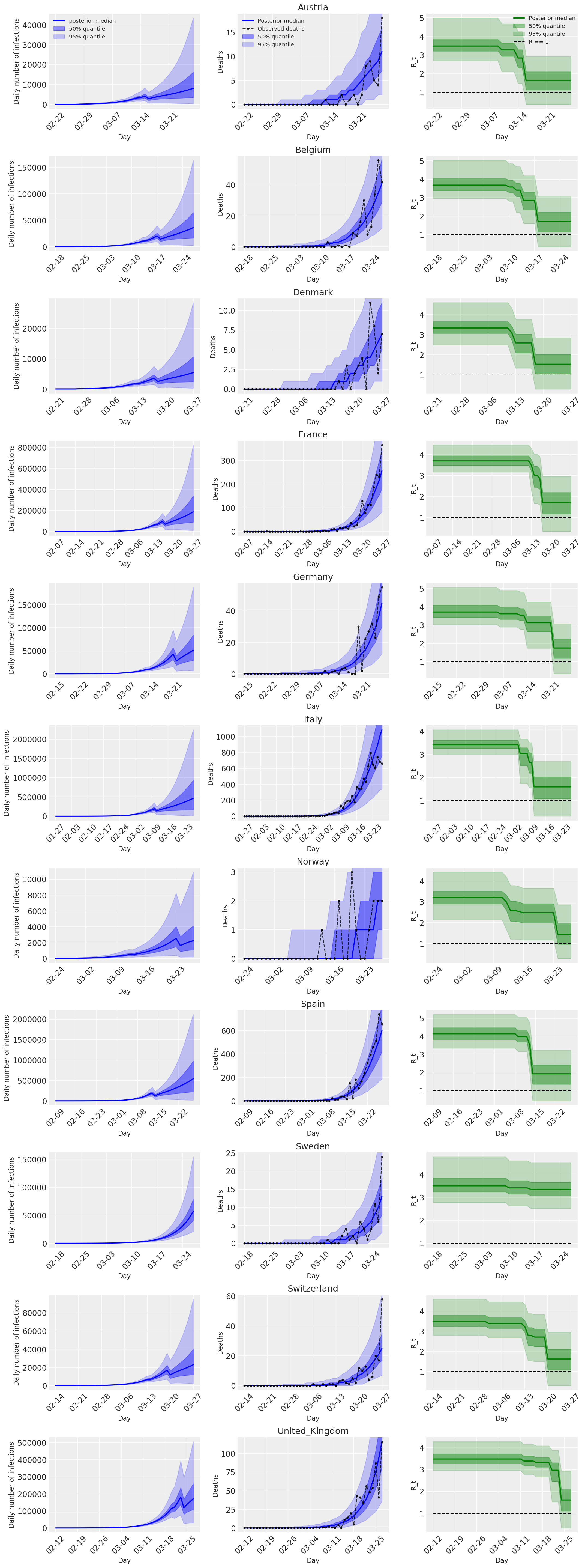
המגרשים הבאים לנתח את ההפצות חזוי האחוריות מעל \(R_t\), מספר מקרי המוות, ומספר הזיהומים, בדומה לניתוח ב פלקסמן ואח. (2020).
total_num_samples = np.prod(posterior['mu'].shape[:2])
# Calculate R_t given parameter estimates.
def rt_samples_batched(mu, intervention_indicators, alpha):
linear_prediction = tf.reduce_sum(
intervention_indicators * alpha[..., np.newaxis, np.newaxis, :], axis=-1)
rt_hat = mu[..., tf.newaxis] * tf.exp(-linear_prediction, name='rt')
return rt_hat
alpha_hat = tf.convert_to_tensor(
posterior['alpha'].reshape(total_num_samples, posterior['alpha'].shape[-1]))
mu_hat = tf.convert_to_tensor(
posterior['mu'].reshape(total_num_samples, num_countries))
rt_hat = rt_samples_batched(mu_hat, intervention_indicators, alpha_hat)
sampled_initial_cases = posterior['initial_cases'].reshape(
total_num_samples, num_countries)
sampled_ifr_noise = posterior['ifr_noise'].reshape(
total_num_samples, num_countries)
psi_hat = posterior['psi'].reshape([total_num_samples])
conv_serial_interval = make_conv_serial_interval(INITIAL_DAYS, TOTAL_DAYS)
conv_fatality_rate = make_conv_fatality_rate(infection_fatality_rate, TOTAL_DAYS)
pred_hat = predict_infections(
intervention_indicators, population_value, sampled_initial_cases, mu_hat,
alpha_hat, conv_serial_interval, INITIAL_DAYS, TOTAL_DAYS)
expected_deaths = predict_deaths(pred_hat, sampled_ifr_noise, conv_fatality_rate)
psi_m = psi_hat[np.newaxis, ..., np.newaxis]
probs = tf.clip_by_value(expected_deaths / (expected_deaths + psi_m), 1e-9, 1.)
predicted_deaths = tfd.NegativeBinomial(
total_count=psi_m, probs=probs).sample()
# Predict counterfactual infections/deaths in the absence of interventions
no_intervention_infections = predict_infections(
intervention_indicators,
population_value,
sampled_initial_cases,
mu_hat,
tf.zeros_like(alpha_hat),
conv_serial_interval,
INITIAL_DAYS, TOTAL_DAYS)
no_intervention_expected_deaths = predict_deaths(
no_intervention_infections, sampled_ifr_noise, conv_fatality_rate)
probs = tf.clip_by_value(
no_intervention_expected_deaths / (no_intervention_expected_deaths + psi_m),
1e-9, 1.)
no_intervention_predicted_deaths = tfd.NegativeBinomial(
total_count=psi_m, probs=probs).sample()
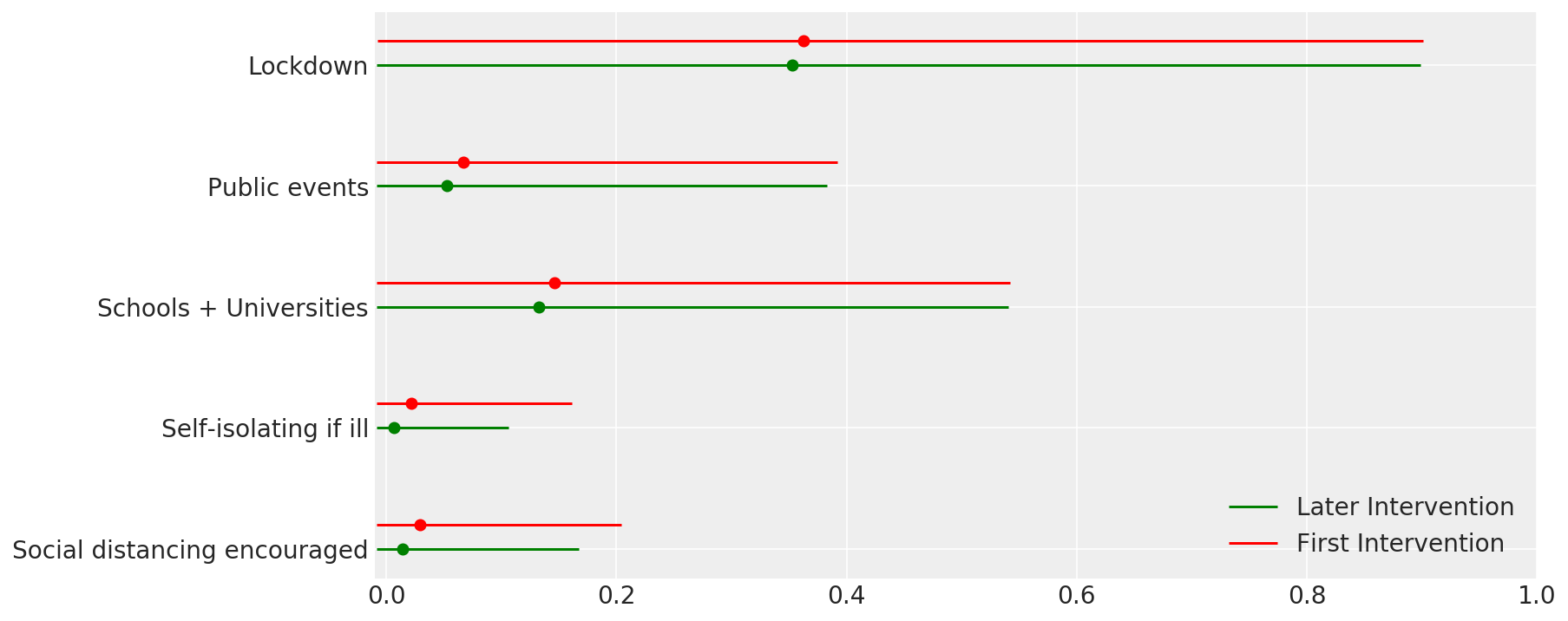
4.1 יעילות ההתערבויות
בדומה לתמונה 4 של Flaxman et al. (2020).
def intervention_effectiveness(alpha):
alpha_adj = 1. - np.exp(-alpha + np.log(1.05) / 6.)
alpha_adj_first = (
1. - np.exp(-alpha - alpha[..., -1:] + np.log(1.05) / 6.))
fig, ax = plt.subplots(1, 1, figsize=[12, 6])
intervention_perm = [2, 1, 3, 4, 0]
percentile_vals = [2.5, 97.5]
jitter = .2
for ind in range(5):
first_low, first_high = tfp.stats.percentile(
alpha_adj_first[..., ind], percentile_vals)
low, high = tfp.stats.percentile(
alpha_adj[..., ind], percentile_vals)
p_ind = intervention_perm[ind]
ax.hlines(p_ind, low, high, label='Later Intervention', colors='g')
ax.scatter(alpha_adj[..., ind].mean(), p_ind, color='g')
ax.hlines(p_ind + jitter, first_low, first_high,
label='First Intervention', colors='r')
ax.scatter(alpha_adj_first[..., ind].mean(), p_ind + jitter, color='r')
if ind == 0:
plt.legend(loc='lower right')
ax.set_yticks(range(5))
ax.set_yticklabels(
[any_intervention_list[intervention_perm.index(p)] for p in range(5)])
ax.set_xlim([-0.01, 1.])
r = fig.patch
r.set_facecolor('white')
intervention_effectiveness(alpha_hat)
4.2 זיהומים, מקרי מוות ו-R_t לפי מדינה
בדומה לתמונה 2 של Flaxman et al. (2020).
import matplotlib.dates as mdates
plot_quantile = True
forecast_days = 0
fig, ax = plt.subplots(11, 3, figsize=(15, 40))
for ind, country in enumerate(COUNTRIES):
num_days = (pd.to_datetime('2020-03-28') - first_days[country]).days + forecast_days
dates = [(first_days[country] + i*pd.to_timedelta(1, 'days')).strftime('%m-%d') for i in range(num_days)]
plot_dates = [dates[i] for i in range(0, num_days, 7)]
# Plot daily number of infections
infections = pred_hat[:, :, ind]
posterior_quantile = np.percentile(infections, [2.5, 25, 50, 75, 97.5], axis=-1)
ax[ind, 0].plot(
dates, posterior_quantile[2, :num_days],
color='b', label='posterior median', lw=2)
if plot_quantile:
ax[ind, 0].fill_between(
dates, posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='b', label='50% quantile', alpha=.4)
ax[ind, 0].fill_between(
dates, posterior_quantile[0, :num_days], posterior_quantile[4, :num_days],
color='b', label='95% quantile', alpha=.2)
ax[ind, 0].set_xticks(plot_dates)
ax[ind, 0].xaxis.set_tick_params(rotation=45)
ax[ind, 0].set_ylabel('Daily number of infections', fontsize='large')
ax[ind, 0].set_xlabel('Day', fontsize='large')
# Plot deaths
ax[ind, 1].set_title(country)
samples = predicted_deaths[:, :, ind]
posterior_quantile = np.percentile(samples, [2.5, 25, 50, 75, 97.5], axis=-1)
ax[ind, 1].plot(
range(num_days), posterior_quantile[2, :num_days],
color='b', label='Posterior median', lw=2)
if plot_quantile:
ax[ind, 1].fill_between(
range(num_days), posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='b', label='50% quantile', alpha=.4)
ax[ind, 1].fill_between(
range(num_days), posterior_quantile[0, :num_days], posterior_quantile[4, :num_days],
color='b', label='95% quantile', alpha=.2)
observed = deaths[ind, :]
observed[observed == -1] = np.nan
ax[ind, 1].plot(
dates, observed[:num_days],
'--o', color='k', markersize=3,
label='Observed deaths', alpha=.8)
ax[ind, 1].set_xticks(plot_dates)
ax[ind, 1].xaxis.set_tick_params(rotation=45)
ax[ind, 1].set_title(country)
ax[ind, 1].set_xlabel('Day', fontsize='large')
ax[ind, 1].set_ylabel('Deaths', fontsize='large')
# Plot R_t
samples = np.transpose(rt_hat[:, ind, :])
posterior_quantile = np.percentile(samples, [2.5, 25, 50, 75, 97.5], axis=-1)
l1 = ax[ind, 2].plot(
dates, posterior_quantile[2, :num_days],
color='g', label='Posterior median', lw=2)
l2 = ax[ind, 2].fill_between(
dates, posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='g', label='50% quantile', alpha=.4)
if plot_quantile:
l3 = ax[ind, 2].fill_between(
dates, posterior_quantile[0, :num_days], posterior_quantile[4, :num_days],
color='g', label='95% quantile', alpha=.2)
l4 = ax[ind, 2].hlines(1., dates[0], dates[-1], linestyle='--', label='R == 1')
ax[ind, 2].set_xlabel('Day', fontsize='large')
ax[ind, 2].set_ylabel('R_t', fontsize='large')
ax[ind, 2].set_xticks(plot_dates)
ax[ind, 2].xaxis.set_tick_params(rotation=45)
fontsize = 'medium'
ax[0, 0].legend(loc='upper left', fontsize=fontsize)
ax[0, 1].legend(loc='upper left', fontsize=fontsize)
ax[0, 2].legend(
bbox_to_anchor=(1., 1.),
loc='upper right',
borderaxespad=0.,
fontsize=fontsize)
plt.tight_layout();
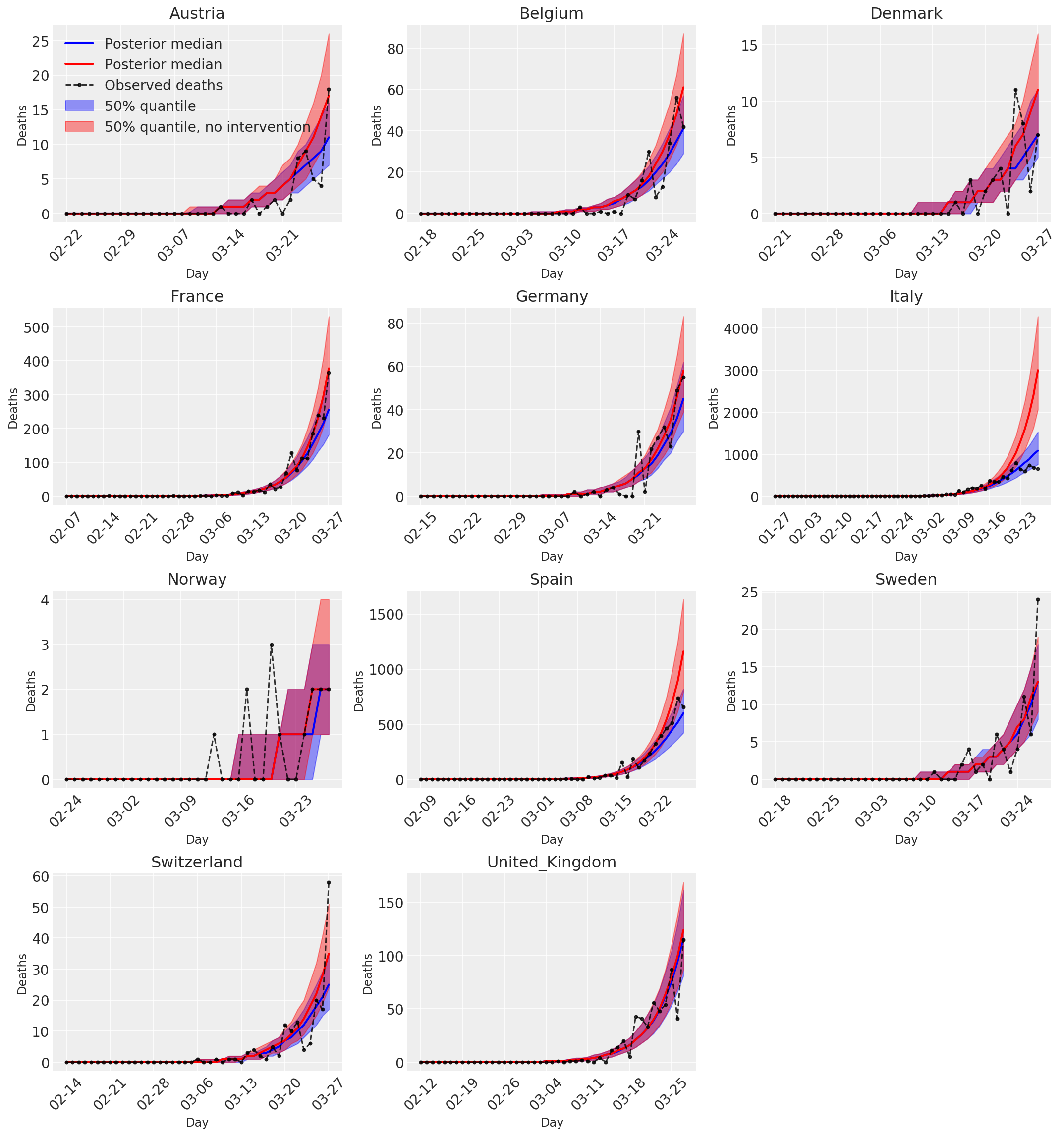
4.3 מספר יומי של מקרי מוות חזויים/חזויים עם ובלי התערבויות
plot_quantile = True
forecast_days = 0
fig, ax = plt.subplots(4, 3, figsize=(15, 16))
ax = ax.flatten()
fig.delaxes(ax[-1])
for country_index, country in enumerate(COUNTRIES):
num_days = (pd.to_datetime('2020-03-28') - first_days[country]).days + forecast_days
dates = [(first_days[country] + i*pd.to_timedelta(1, 'days')).strftime('%m-%d') for i in range(num_days)]
plot_dates = [dates[i] for i in range(0, num_days, 7)]
ax[country_index].set_title(country)
quantile_vals = [.025, .25, .5, .75, .975]
samples = predicted_deaths[:, :, country_index].numpy()
quantiles = []
psi_m = psi_hat[np.newaxis, ..., np.newaxis]
probs = tf.clip_by_value(expected_deaths / (expected_deaths + psi_m), 1e-9, 1.)
predicted_deaths_dist = tfd.NegativeBinomial(
total_count=psi_m, probs=probs)
posterior_quantile = np.percentile(samples, [2.5, 25, 50, 75, 97.5], axis=-1)
ax[country_index].plot(
dates, posterior_quantile[2, :num_days],
color='b', label='Posterior median', lw=2)
if plot_quantile:
ax[country_index].fill_between(
dates, posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='b', label='50% quantile', alpha=.4)
samples_counterfact = no_intervention_predicted_deaths[:, :, country_index]
posterior_quantile = np.percentile(samples_counterfact, [2.5, 25, 50, 75, 97.5], axis=-1)
ax[country_index].plot(
dates, posterior_quantile[2, :num_days],
color='r', label='Posterior median', lw=2)
if plot_quantile:
ax[country_index].fill_between(
dates, posterior_quantile[1, :num_days], posterior_quantile[3, :num_days],
color='r', label='50% quantile, no intervention', alpha=.4)
observed = deaths[country_index, :]
observed[observed == -1] = np.nan
ax[country_index].plot(
dates, observed[:num_days],
'--o', color='k', markersize=3,
label='Observed deaths', alpha=.8)
ax[country_index].set_xticks(plot_dates)
ax[country_index].xaxis.set_tick_params(rotation=45)
ax[country_index].set_title(country)
ax[country_index].set_xlabel('Day', fontsize='large')
ax[country_index].set_ylabel('Deaths', fontsize='large')
ax[0].legend(loc='upper left')
plt.tight_layout(pad=1.0);