 عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
A [حباك] (https://en.wikipedia.org/wiki/Copula_ (probability_theory٪ 29) هو النهج التقليدي لالتقاط الاعتماد بين المتغيرات العشوائية، وأكثر رسميا، وحباك هو متعدد المتغيرات توزيع \(C(U_1, U_2, ...., U_n)\) بحيث تهميش يعطي \(U_i \sim \text{Uniform}(0, 1)\).
تعتبر Copulas مثيرة للاهتمام لأنه يمكننا استخدامها لإنشاء توزيعات متعددة المتغيرات بهوامش عشوائية. هذه هي الوصفة:
- باستخدام جزءا لا يتجزأ احتمال تحويل يتحول تعسفية RV مستمرة \(X\) في زي واحد \(F_X(X)\)، حيث \(F_X\) هو CDF من \(X\).
- إعطاء حباك (ويقول ذات المتغيرين) \(C(U, V)\)، لدينا أن \(U\) و \(V\) ديك التوزيعات الهامشية موحدة.
- الآن نظرا لدينا RV للاهتمام \(X, Y\)، خلق جديد توزيع \(C'(X, Y) = C(F_X(X), F_Y(Y))\). والربح البسيط ل \(X\) و \(Y\) هي تلك التي كنا المطلوب.
الهامش وحيد المتغير وبالتالي قد يكون من الأسهل قياسه و / أو نمذجه. يتيح الكوبولا البدء من الهامش مع تحقيق ارتباط تعسفي بين الأبعاد.
غاوسي كوبولا
لتوضيح كيفية إنشاء copulas ، ضع في اعتبارك حالة التقاط التبعية وفقًا للارتباطات الغوسية متعددة المتغيرات. A التمويه حباك هو واحد التي قدمها \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) حيث \(\Phi_\Sigma\) يمثل CDF من MultivariateNormal، مع التغاير \(\Sigma\) ويعني 0، و \(\Phi^{-1}\) هو CDF معكوس للمستوى الطبيعي.
يؤدي تطبيق معكوس CDF العادي إلى تشويه الأبعاد الموحدة ليتم توزيعها بشكل طبيعي. تطبيق CDF العادي متعدد المتغيرات ثم يسحق التوزيع ليكون موحدًا بشكل هامشي ومع ارتباطات غاوسية.
وهكذا، ما نحصل عليه هو أن التمويه حباك هو التوزيع على وحدة الزائدي \([0, 1]^n\) مع الربح البسيط موحدة.
تعريف على هذا النحو، والتمويه حباك يمكن تنفيذها مع tfd.TransformedDistribution ومناسبة Bijector . وهذا يعني، أننا تقوم بتحويل MultivariateNormal، عن طريق استخدام التوزيع الطبيعي معكوس CDF، التي تنفذها tfb.NormalCDF bijector.
أدناه، علينا أن ننفذ التمويه حباك مع واحد تبسيط افتراض: أن التغاير ومعلمات بعامل Cholesky (بالتالي التغاير ل MultivariateNormalTriL ). (يمكن للمرء أن استخدام البعض tf.linalg.LinearOperators لترميز مختلفة الافتراضات خالية من المصفوفة).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
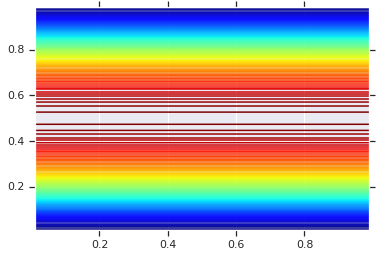
ومع ذلك ، فإن القوة من هذا النموذج تستخدم التحويل المتكامل الاحتمالي ، لاستخدام الكوبولا على RVs التعسفية. بهذه الطريقة ، يمكننا تحديد الهامش التعسفي ، واستخدام الكوبولا لربطها معًا.
نبدأ بنموذج:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
واستخدام حباك للحصول على ذات المتغيرين RV \(Z\)، التي لديها الربح البسيط كوماراسوامي و جامبل .
سنبدأ بالتخطيط لتوزيع المنتج الذي تم إنشاؤه بواسطة هذين المركبين. هذا فقط ليكون بمثابة نقطة مقارنة عندما نطبق Copula.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
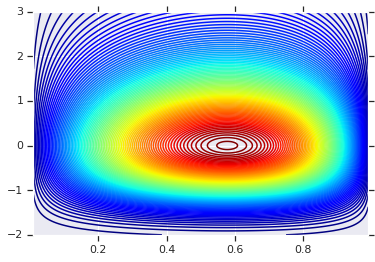
التوزيع المشترك مع الهامش المختلفة
نستخدم الآن وحدة Gaussian copula لربط التوزيعات ببعضها البعض ، ورسم ذلك. مرة أخرى لدينا أداة الاختيار و TransformedDistribution تطبيق المناسب Bijector للحصول على الربح البسيط الذي تم اختياره.
على وجه التحديد، ونحن نستخدم Blockwise bijector الذي ينطبق bijectors مختلفة في أجزاء مختلفة من ناقلات (التي لا تزال تحول bijective).
الآن يمكننا تحديد الكوبولا التي نريدها. بالنظر إلى قائمة الهوامش المستهدفة (المشفرة على شكل bijectors) ، يمكننا بسهولة إنشاء توزيع جديد يستخدم الكوبولا وله الهامش المحدد.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
أخيرًا ، دعنا نستخدم هذه الكوبولا الغاوسية. سنستخدم Cholesky من \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\)، والتي سوف تقابل الفروق 1، وارتباط \(\rho\) لمتعدد المتغيرات وضعها الطبيعي.
سننظر في بعض الحالات:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
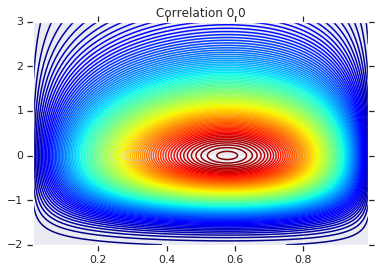
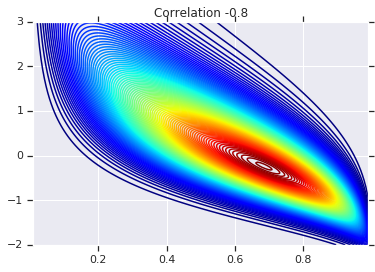
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
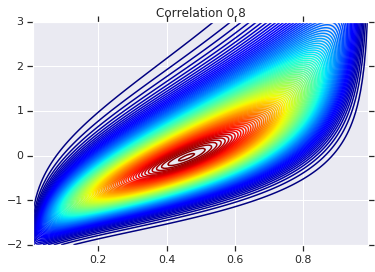
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
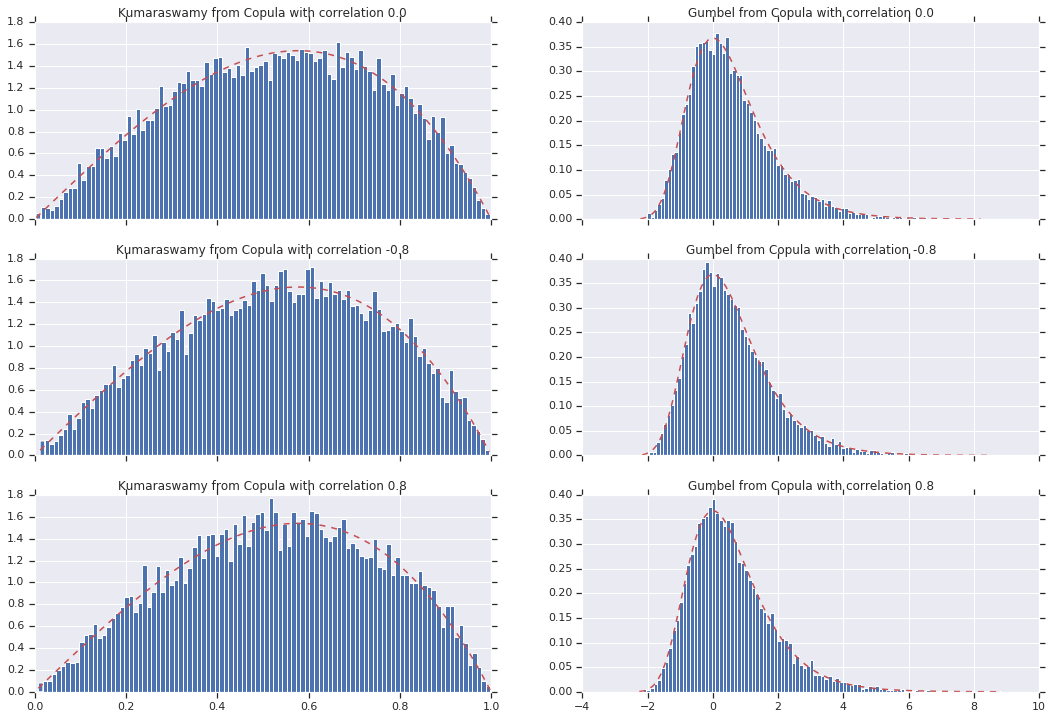
أخيرًا ، لنتحقق من أننا حصلنا بالفعل على الهامش الذي نريده.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
استنتاج
وها نحن ذا! لقد أثبت أن نتمكن من بناء التمويه Copulas باستخدام Bijector API.
أكثر عموما، والكتابة bijectors باستخدام Bijector API ويؤلف لهم التوزيع، يمكن أن تخلق العائلات الغنية من توزيعات لنمذجة مرونة.
