 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запускаем в Google Colab Запускаем в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
Модель линейных смешанных эффектов - это простой подход к моделированию структурированных линейных отношений (Harville, 1997; Laird and Ware, 1982). Каждая точка данных состоит из входных данных разного типа, разделенных на группы, и выходных данных с действительными значениями. Линейная модель смешанных эффектов представляет собой иерархическая модель: она делит статистическую силу между группами с целью улучшения выводов о какой - либо конкретной точке данных.
В этом руководстве мы демонстрируем модели линейных смешанных эффектов на реальном примере в TensorFlow Probability. Мы будем использовать JointDistributionCoroutine и цепи Маркова Монте - Карло ( tfp.mcmc ) модулей.
Зависимости и предварительные условия
Импорт и настройки
import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')
Делайте вещи быстро!
Прежде чем мы углубимся, давайте убедимся, что мы используем графический процессор для этой демонстрации.
Для этого выберите «Время выполнения» -> «Изменить тип времени выполнения» -> «Аппаратный ускоритель» -> «Графический процессор».
Следующий фрагмент кода подтвердит, что у нас есть доступ к графическому процессору.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
Данные
Мы используем InstEval набор данных из популярного lme4 пакета в R (Bates и др., 2015). Это набор данных о курсах и их оценочных рейтингах. Каждый курс включает в себя метаданные , такие как students , instructors и departments , а также переменная ответ интерес представляет оценка оценки.
def load_insteval():
"""Loads the InstEval data set.
It contains 73,421 university lecture evaluations by students at ETH
Zurich with a total of 2,972 students, 2,160 professors and
lecturers, and several student, lecture, and lecturer attributes.
Implementation is built from the `observations` Python package.
Returns:
Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
dictionary `metadata` of column headers (feature names).
"""
url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
'lme4/InstEval.csv')
with requests.Session() as s:
download = s.get(url)
f = download.content.decode().splitlines()
iterator = csv.reader(f)
columns = next(iterator)[1:]
x_train = np.array([row[1:] for row in iterator], dtype=np.int)
metadata = {'columns': columns}
return x_train, metadata
Загружаем и предварительно обрабатываем набор данных. Мы храним 20% данных, поэтому мы можем оценить нашу подобранную модель по невидимым точкам данных. Ниже мы визуализируем первые несколько рядов.
data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
'd': 'instructors',
'dept': 'departments',
'y': 'ratings'})
data['students'] -= 1 # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes
train = data.sample(frac=0.8)
test = data.drop(train.index)
train.head()
Мы создали набор данных в терминах features словаря входов и labels на выходе соответствует рейтингам. Каждая функция кодируется как целое число, а каждая метка (оценочная оценка) кодируется как число с плавающей запятой.
get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
k: get_value(train, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)
features_test = {k: get_value(test, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)
num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]
print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)
Number of students: 2972 Number of instructors: 1128 Number of departments: 14 Number of observations: 58737
Модель
Типичная линейная модель предполагает независимость, где любая пара точек данных имеет постоянную линейную зависимость. В InstEval наборе данных наблюдений возникают в группах , каждая из которых может иметь различные наклоны и отрезки. Модели линейных смешанных эффектов, также известные как иерархические линейные модели или многоуровневые линейные модели, отражают это явление (Gelman & Hill, 2006).
Примеры этого явления включают:
- Студенты. Наблюдения студента не являются независимыми: некоторые студенты могут систематически давать низкие (или высокие) оценки лекций.
- Инструкторы. Наблюдения инструктора не являются независимыми: мы ожидаем, что хорошие учителя обычно имеют хорошие оценки, а плохие учителя обычно имеют плохие оценки.
- Отделы. Наблюдения отдела не являются независимыми: в некоторых отделах обычно может быть сухой материал или более строгая сортировка и, следовательно, они будут оценены ниже, чем другие.
Для того, чтобы захватить это, напомним , что для набора данных \(N\times D\) показывает \(\mathbf{X}\) и \(N\) этикетки \(\mathbf{y}\), линейной регрессии постулирует модели
\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]
где есть наклон вектора \(\beta\in\mathbb{R}^D\), отсекаемый \(\alpha\in\mathbb{R}\), и случайный шум \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Мы говорим , что \(\beta\) и \(\alpha\) являются «фиксированными эффектами»: они эффекты проводятся постоянной среди населения точек данных \((x, y)\). Эквивалентная формулировка уравнения в качестве правдоподобия \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\). Эта вероятность максимальна во время вывода, чтобы найти точечные оценки \(\beta\) и \(\alpha\) , которые соответствуют данным.
Модель линейных смешанных эффектов расширяет линейную регрессию как
\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]
где до сих пор наклон вектора \(\beta\in\mathbb{R}^P\), отсекаемый \(\alpha\in\mathbb{R}\), и случайный шум \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Кроме того, существует термин \(\mathbf{Z}\eta\), где \(\mathbf{Z}\) представляет собой матрицу функции и \(\eta\in\mathbb{R}^Q\) представляет собой вектор случайных трасс; \(\eta\) имеет нормальное распределение с параметром дисперсии компонент \(\sigma^2\). \(\mathbf{Z}\) формируется путем разделения исходной \(N\times D\) особенности матрицы в терминах новой \(N\times P\) матрицы \(\mathbf{X}\) и \(N\times Q\) матрицы \(\mathbf{Z}\), где \(P + Q=D\): этот раздел позволяет нам моделировать функции по отдельности , используя фиксированные эффекты \(\beta\) и скрытые переменная \(\eta\) соответственно.
Мы говорим , что скрытые переменные \(\eta\) являются «случайными эффектами»: они эффекты , которые изменяются среди населения (хотя они могут быть постоянными по субпопуляции). В частности, потому , что случайные эффекты \(\eta\) имеет среднее 0, средние подписи данных в захватываются \(\mathbf{X}\beta + \alpha\). Случайные эффекты компонента \(\mathbf{Z}\eta\) вариация захватывает в данных: например, «инструктор # 54 оцениваются в 1,4 баллов выше , чем средний» .
В этом уроке мы устанавливаем следующие эффекты:
- Фиксированные эффекты:
service.serviceявляется бинарным ковариатой , соответствующим принадлежит ли курс главному управлению инструктором. Независимо от того , сколько дополнительных данных мы собираем, может принимать только значения \(0\) и \(1\). - Случайные эффекты:
students,instructorsиdepartments. Учитывая больше наблюдений населения за оценками курсов, мы можем смотреть на новых студентов, преподавателей или факультетов.
В синтаксисе пакета R lme4 (Bates et al., 2015) модель можно резюмировать как
ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1
где x обозначает фиксированный эффект, (1|x) обозначает случайный эффект для x , и 1 обозначает свободный член.
Мы реализуем эту модель ниже как JointDistribution. Для того, чтобы иметь лучшую поддержку для отслеживания параметров (например, мы хотим , чтобы отслеживать все tf.Variable в model.trainable_variables ), мы реализуем шаблон модели как tf.Module .
class LinearMixedEffectModel(tf.Module):
def __init__(self):
# Set up fixed effects and other parameters.
# These are free parameters to be optimized in E-steps
self._intercept = tf.Variable(0., name="intercept") # alpha in eq
self._effect_service = tf.Variable(0., name="effect_service") # beta in eq
self._stddev_students = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_students") # sigma in eq
self._stddev_instructors = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_instructors") # sigma in eq
self._stddev_departments = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_departments") # sigma in eq
def __call__(self, features):
model = tfd.JointDistributionSequential([
# Set up random effects.
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_students),
scale_identity_multiplier=self._stddev_students),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_instructors),
scale_identity_multiplier=self._stddev_instructors),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_departments),
scale_identity_multiplier=self._stddev_departments),
# This is the likelihood for the observed.
lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
tfd.Normal(
loc=(self._effect_service * features["service"] +
tf.gather(effect_students, features["students"], axis=-1) +
tf.gather(effect_instructors, features["instructors"], axis=-1) +
tf.gather(effect_departments, features["departments"], axis=-1) +
self._intercept),
scale=1.),
reinterpreted_batch_ndims=1)
])
# To enable tracking of the trainable variables via the created distribution,
# we attach a reference to `self`. Since all TFP objects sub-class
# `tf.Module`, this means that the following is possible:
# LinearMixedEffectModel()(features_train).trainable_variables
# ==> tuple of all tf.Variables created by LinearMixedEffectModel.
model._to_track = self
return model
lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)
lmm_train.trainable_variables
(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)
В качестве вероятностной графической программы мы также можем визуализировать структуру модели в терминах ее вычислительного графа. Этот граф кодирует поток данных по случайным переменным в программе, показывая их взаимосвязи в терминах графической модели (Jordan, 2003).
Как статистический инструмент, мы можем взглянуть на график, чтобы лучше видеть, например, что intercept и effect_service условно зависимые данные ratings ; это может быть труднее увидеть из исходного кода, если программа написана с классами, перекрестными ссылками между модулями и / или подпрограммами. В качестве вычислительного инструмента, мы могли бы также заметить скрытые переменный поток в ratings переменных через tf.gather опс. Это может быть узким местом на определенных аппаратных ускорителей , если индексация Tensor s дорого; визуализация графика делает это очевидным.
lmm_train.resolve_graph()
(('effect_students', ()),
('effect_instructors', ()),
('effect_departments', ()),
('x', ('effect_departments', 'effect_instructors', 'effect_students')))
Оценка параметров
С учетом данных, цель умозаключений является , чтобы соответствовать модели фиксированных эффектов наклона \(\beta\), перехватывают \(\alpha\), и дисперсия компонент параметра \(\sigma^2\). Принцип максимального правдоподобия формализует эту задачу как
\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]
В этом руководстве мы используем алгоритм Монте-Карло EM, чтобы максимизировать эту предельную плотность (Dempster et al., 1977; Wei and Tanner, 1990). Мы выполняем цепной метод Монте-Карло Маркова, чтобы вычислить математическое ожидание условного правдоподобия относительно случайные эффекты («E-шаг»), и мы выполняем градиентный спуск, чтобы максимизировать ожидания относительно параметров («M-шаг»):
Для E-шага мы устанавливаем гамильтониан Монте-Карло (HMC). Он принимает текущее состояние - эффекты студента, преподавателя и отдела - и возвращает новое состояние. Мы присваиваем новое состояние переменным TensorFlow, которые будут обозначать состояние цепочки HMC.
Для M-шага мы используем апостериорную выборку из HMC для вычисления несмещенной оценки предельного правдоподобия с точностью до константы. Затем мы применяем его градиент по отношению к интересующим параметрам. Это дает несмещенный шаг стохастического спуска для предельного правдоподобия. Мы реализуем это с помощью оптимизатора Adam TensorFlow и минимизируем негатив маргинала.
target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]
# For debugging
target_log_prob_fn(*current_state)
<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>
# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.015,
num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)
@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
next_state, next_kernel_results = hmc.one_step(
current_state=current_state,
previous_kernel_results=kernel_results)
return next_state, next_kernel_results
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
with tf.GradientTape() as tape:
loss = -target_log_prob_fn(*current_state)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
Мы выполняем этап разминки, который запускает одну цепочку MCMC для ряда итераций, так что обучение может быть инициализировано в пределах апостериорной вероятностной массы. Затем мы запускаем цикл обучения. Он совместно выполняет шаги E и M и записывает значения во время обучения.
num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])
# Run warm-up stage.
for t in range(num_warmup_iters):
current_state, kernel_results = one_e_step(current_state, kernel_results)
num_accepted += kernel_results.is_accepted.numpy()
if t % 500 == 0 or t == num_warmup_iters - 1:
print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
t, num_accepted / (t + 1)))
num_accepted = 0 # reset acceptance rate counter
# Run training.
for t in range(num_iters):
# run 5 MCMC iterations before every joint EM update
for _ in range(5):
current_state, kernel_results = one_e_step(current_state, kernel_results)
loss = one_m_step(current_state)
effect_students_samples[t, :] = current_state[0].numpy()
effect_instructors_samples[t, :] = current_state[1].numpy()
effect_departments_samples[t, :] = current_state[2].numpy()
num_accepted += kernel_results.is_accepted.numpy()
loss_history[t] = loss.numpy()
if t % 500 == 0 or t == num_iters - 1:
print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
t, num_accepted / (t + 1), loss_history[t]))
Warm-Up Iteration: 0 Acceptance Rate: 1.000 Warm-Up Iteration: 500 Acceptance Rate: 0.754 Warm-Up Iteration: 999 Acceptance Rate: 0.707 Iteration: 0 Acceptance Rate: 1.000 Loss: 98220.266 Iteration: 500 Acceptance Rate: 0.703 Loss: 96003.969 Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609 Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891
Вы также можете написать разминку для цикла в tf.while_loop , и этап обучения в tf.scan или tf.while_loop для еще более быстрого вывода. Например:
@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
_, next_state, next_kernel_results = tf.while_loop(
cond=lambda i, state, pkr: i < k,
body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
loop_vars=(tf.constant(0), current_state, kernel_results)
)
return next_state, next_kernel_results
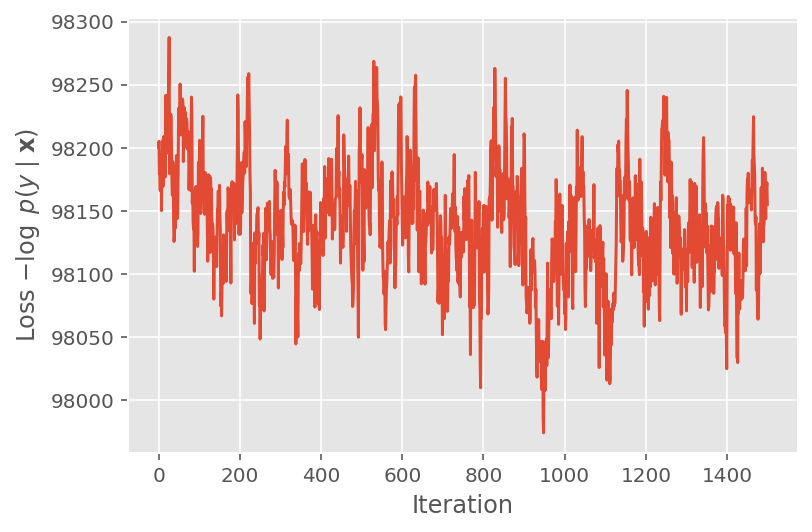
Выше мы не запускали алгоритм, пока не был обнаружен порог сходимости. Чтобы проверить, было ли обучение разумным, мы проверяем, действительно ли функция потерь имеет тенденцию сходиться во время итераций обучения.
plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()
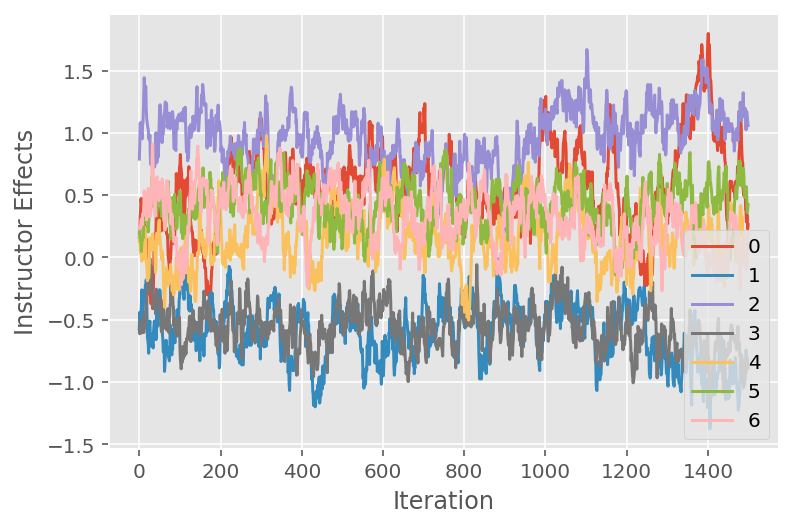
Мы также используем график трассировки, который показывает траекторию алгоритма Монте-Карло цепи Маркова в определенных скрытых измерениях. Ниже мы видим, что конкретные эффекты инструктора действительно осмысленно переходят от своего начального состояния и исследуют пространство состояний. График трассировки также указывает на то, что эффекты у разных преподавателей различаются, но с одинаковым поведением микширования.
for i in range(7):
plt.plot(effect_instructors_samples[:, i])
plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()
Критика
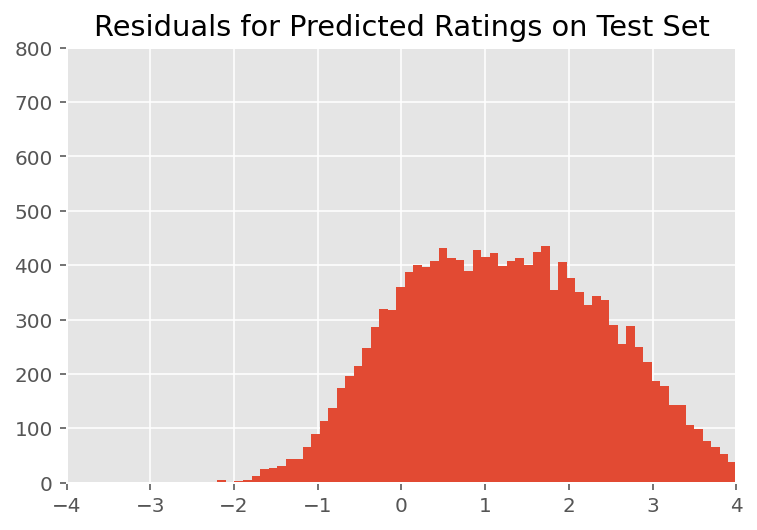
Выше мы подогнали модель. Теперь мы рассмотрим критику его соответствия с использованием данных, которые позволяют нам изучить и лучше понять модель. Одним из таких методов является график остатков, который отображает разницу между предсказаниями модели и достоверностью данных для каждой точки данных. Если модель верна, то их разница должна быть стандартно нормально распределенной; любые отклонения от этого шаблона на графике указывают на несоответствие модели.
Мы строим остаточный график, сначала формируя апостериорное прогнозирующее распределение по рейтингам, которое заменяет априорное распределение случайных эффектов его апостериорными заданными обучающими данными. В частности, мы прогоняем модель вперед и перехватываем ее зависимость от предшествующих случайных эффектов с их предполагаемыми апостериорными средними2.
lmm_test = lmm_jointdist(features_test)
[
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
] = [
np.mean(x, axis=0).astype(np.float32) for x in [
effect_students_samples,
effect_instructors_samples,
effect_departments_samples
]
]
# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
value=(
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
))
ratings_prediction = ratings_posterior.mean()
При визуальном осмотре остатки выглядят несколько стандартно нормально распределенными. Однако подгонка не идеальна: существует большая вероятностная масса в хвостах, чем при нормальном распределении, что указывает на то, что модель может улучшить свою подгонку, ослабив свои предположения о нормальности.
В частности, несмотря на то, что является наиболее распространенным использовать нормальное распределение для оценки модели в InstEval наборе данных, более пристальный взгляд на данных показывает , что рейтинги оценки , конечно, фактически являются порядковыми значениями от 1 до 5. Это говорит о том, что мы должны использовать порядковое распределение или даже категориальное, если у нас достаточно данных, чтобы отбросить относительный порядок. Это однострочное изменение модели выше; применим тот же код вывода.
plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()
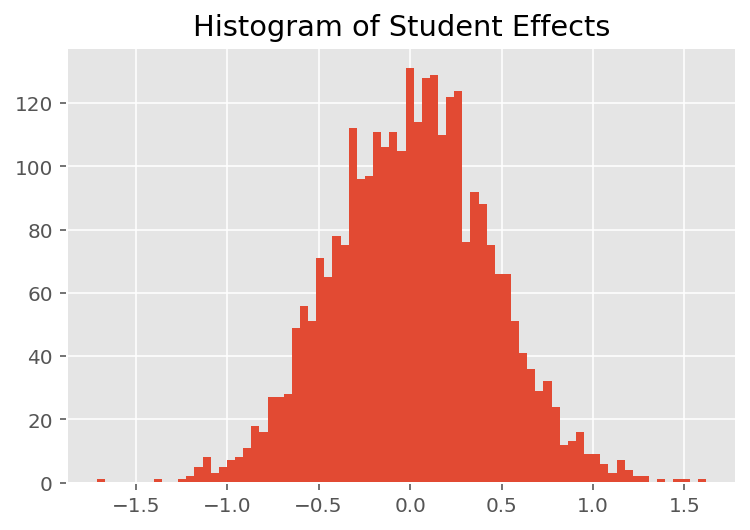
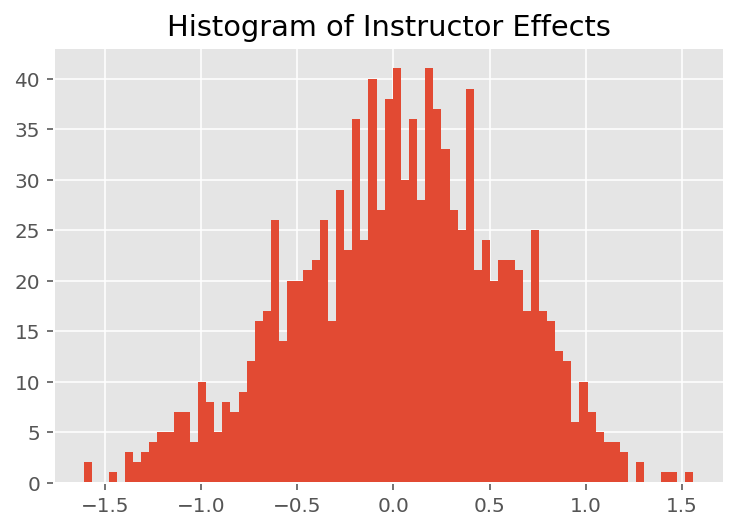
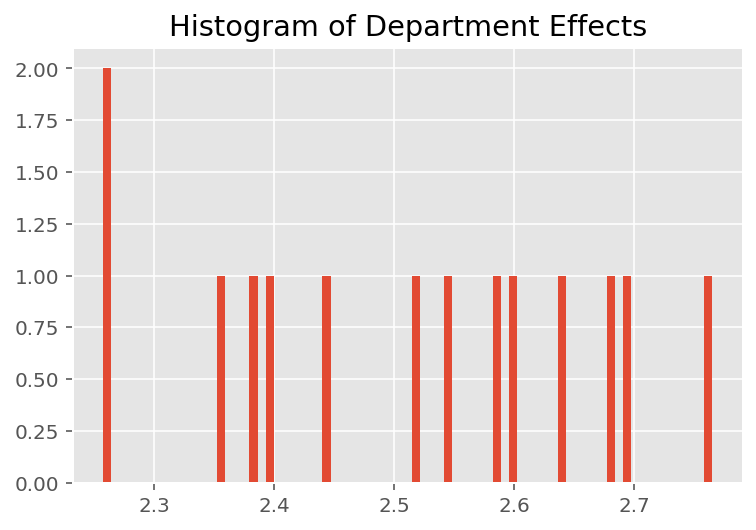
Чтобы изучить, как модель делает индивидуальные прогнозы, мы смотрим на гистограмму эффектов для студентов, преподавателей и кафедр. Это позволяет нам понять, как отдельные элементы в векторе признаков точки данных имеют тенденцию влиять на результат.
Неудивительно, что ниже мы видим, что каждый студент обычно мало влияет на оценку преподавателя. Интересно, что мы видим, что отдел, к которому принадлежит преподаватель, имеет большое влияние.
plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()
plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()
plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()
Сноски
¹ Модели линейных смешанных эффектов - это особый случай, когда мы можем аналитически вычислить его предельную плотность. Для целей этого руководства мы демонстрируем метод Монте-Карло EM, который более легко применим к неаналитическим предельным плотностям, например, если бы вероятность была расширена до категориальной, а не нормальной.
² Для простоты мы формируем среднее значение прогнозируемого распределения, используя только один прямой проход модели. Это делается путем кондиционирования апостериорного среднего и действительно для линейных моделей со смешанными эффектами. Однако в целом это неверно: среднее значение апостериорного прогностического распределения обычно трудно поддается обработке и требует взятия эмпирического среднего значения по нескольким прямым проходам модели с заданными апостериорными выборками.
Благодарности
Этот учебник был изначально написан на Эдварде 1.0 ( источник ). Мы благодарим всех участников, написавших и отредактировавших эту версию.
использованная литература
Дуглас Бейтс и Мартин Махлер, Бен Болкер и Стив Уокер. Подбор линейных моделей со смешанными эффектами с помощью lme4. Журнал статистического программного обеспечения, 67 (1): 1-48, 2015.
Артур П. Демпстер, Нэн М. Лэрд и Дональд Б. Рубин. Максимальная вероятность получения неполных данных с помощью алгоритма EM. Журнал Королевского статистического общества, Series B (методологический), 1-38, 1977.
Эндрю Гельман и Дженнифер Хилл. Анализ данных с использованием регрессионных и многоуровневых / иерархических моделей. Издательство Кембриджского университета, 2006.
Дэвид А. Харвилл. Подходы максимального правдоподобия к оценке компонентов дисперсии и к связанным проблемам. Журнал Американской статистической ассоциации, 72 (358): 320-338, 1977.
Майкл И. Джордан. Введение в графические модели. Технический отчет, 2003 г.
Нэн М. Лэрд и Джеймс Уэр. Модели со случайными эффектами для продольных данных. Биометрия, 963-974, 1982.
Грег Вей и Мартин А. Таннер. Реализация алгоритма EM и алгоритмов увеличения данных для бедняков методом Монте-Карло. Журнал Американской статистической ассоциации, 699-704, 1990.
