Bu örnek PyMC3 örnek defterden taşıdık Düzeyli Modelleme için Bayes Yöntemleri Üzerine Bir Okuma
 TensorFlow.org'da görüntüleyin TensorFlow.org'da görüntüleyin |  Google Colab'da çalıştırın Google Colab'da çalıştırın |  Kaynağı GitHub'da görüntüleyin Kaynağı GitHub'da görüntüleyin |  Not defterini indir Not defterini indir |
Bağımlılıklar ve Ön Koşullar
İçe aktarmak
import collections
import os
from six.moves import urllib
import daft as daft
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import warnings
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
tfk = tf.keras
tfkl = tf.keras.layers
tfpl = tfp.layers
tfd = tfp.distributions
tfb = tfp.bijectors
warnings.simplefilter('ignore')
1. Giriş
Bu CoLab biz popüler Radon veri kümesini kullanarak hiyerarşik lineer model modeli karmaşıklığı çeşitli derecelerde (HLMs) uyacaktır. TFP ilkellerini ve Markov Zinciri Monte Carlo araç setini kullanacağız.
Verilere daha iyi uyum sağlamak için amacımız, veri setinde bulunan doğal hiyerarşik yapıdan yararlanmaktır. Geleneksel yaklaşımlarla başlıyoruz: tamamen havuzlanmış ve havuzlanmamış modeller. Çok düzeyli modellerle devam ediyoruz: kısmi havuzlama modellerini, grup düzeyinde tahmin edicileri ve bağlamsal etkileri keşfetme.
İlgili bir dizüstü bilgisayar için de kontrol Radon veri kümesi üzerinde TFP kullanmanın HLMs uydurma {TF olasılık, R stan} lineer karma etkisi Regresyon .
Burada materyalin hakkında herhangi bir sorunuz varsa, temas tereddüt (veya katılmak) yok TensorFlow Olasılık posta listesi . Yardım etmekten mutluluk duyarız.
2 Çok Düzeyli Modellemeye Genel Bakış
Çok Düzeyli Modelleme için Bayes Yöntemleri Üzerine Bir Astar
Hiyerarşik veya çok seviyeli modelleme, regresyon modellemenin bir genellemesidir.
Çok seviyeli modeller, kurucu model parametrelerine olasılık dağılımlarının verildiği regresyon modelleridir. Bu, model parametrelerinin gruba göre değişmesine izin verildiği anlamına gelir. Gözlem birimleri genellikle doğal olarak kümelenir. Kümeleme, kümelerin rastgele örneklenmesine ve kümeler içinde rastgele örneklemeye rağmen, gözlemler arasında bağımlılığa neden olur.
Hiyerarşik bir model, parametrelerin iç içe yerleştirildiği belirli bir çok düzeyli modeldir. Bazı çok düzeyli yapılar hiyerarşik değildir.
örneğin "ülke" ve "yıl" iç içe değildir, ancak ayrı, ancak örtüşen parametre kümelerini temsil edebilirler. Bu konuyu bir çevresel epidemiyoloji örneği kullanarak motive edeceğiz.
Örnek: Radon kirliliği (Gelman ve Hill 2006)
Radon, evlere yerle temas noktalarından giren radyoaktif bir gazdır. Sigara içmeyenlerde akciğer kanserinin birincil nedeni olan bir kanserojendir. Radon seviyeleri haneden haneye büyük farklılıklar gösterir.
EPA, 80.000 evde radon seviyeleri üzerine bir çalışma yaptı. İki önemli belirleyici şunlardır: 1. Bodrum katında veya birinci katta ölçüm (bodrumlarda radon daha yüksek) 2. İlçe uranyum seviyesi (radon seviyeleri ile pozitif korelasyon)
Minnesota'daki radon seviyelerini modellemeye odaklanacağız. Bu örnekteki hiyerarşi, her ilçedeki hanelerdir.
3 Veri Müdahalesi
Bu bölümde elde radon veri kümesini ve bazı asgari ön işlemeyi yapmak.
def load_and_preprocess_radon_dataset(state='MN'):
"""Preprocess Radon dataset as done in "Bayesian Data Analysis" book.
We filter to Minnesota data (919 examples) and preprocess to obtain the
following features:
- `log_uranium_ppm`: Log of soil uranium measurements.
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
# For any missing or invalid activity readings, we'll use a value of `0.1`.
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
county_name = sorted(df.county.unique())
df['county'] = df.county.astype(
pd.api.types.CategoricalDtype(categories=county_name)).cat.codes
county_name = list(map(str.strip, county_name))
df['log_radon'] = df['radon'].apply(np.log)
df['log_uranium_ppm'] = df['Uppm'].apply(np.log)
df = df[['idnum', 'log_radon', 'floor', 'county', 'log_uranium_ppm']]
return df, county_name
radon, county_name = load_and_preprocess_radon_dataset()
num_counties = len(county_name)
num_observations = len(radon)
# Create copies of variables as Tensors.
county = tf.convert_to_tensor(radon['county'], dtype=tf.int32)
floor = tf.convert_to_tensor(radon['floor'], dtype=tf.float32)
log_radon = tf.convert_to_tensor(radon['log_radon'], dtype=tf.float32)
log_uranium = tf.convert_to_tensor(radon['log_uranium_ppm'], dtype=tf.float32)
radon.head()
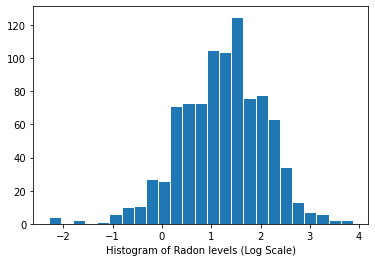
Radon seviyelerinin dağılımı (log ölçeği):
plt.hist(log_radon.numpy(), bins=25, edgecolor='white')
plt.xlabel("Histogram of Radon levels (Log Scale)")
plt.show()
4 Geleneksel Yaklaşımlar
Radona maruz kalmayı modellemeye yönelik iki geleneksel alternatif, önyargı-varyans değiş tokuşunun iki uç noktasını temsil eder:
Komple Havuzlama:
Tüm ilçelere aynı davranın ve tek bir radon seviyesi tahmin edin.
\[y_i = \alpha + \beta x_i + \epsilon_i\]
Havuzlama Yok:
Her ilçede bağımsız olarak model radon.
\(y_i = \alpha_{j[i]} + \beta x_i + \epsilon_i\) burada \(j = 1,\ldots,85\)
Hatalar \(\epsilon_i\) evlerin arasında ölçüm hatası, zamansal içinde içi varyasyonu veya varyasyonunu temsil edebilir.
4.1 Komple Havuzlama Modeli
pgm = daft.PGM([7, 3.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"alpha_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
3,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"beta_prior",
r"$\mathcal{N}(0, 10^5)$",
2.5,
3,
fixed=True,
offset=(10, 5)))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4.5,
3,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("alpha", r"$\alpha$", 1, 2))
pgm.add_node(daft.Node("beta", r"$\beta$", 2.5, 2))
pgm.add_node(daft.Node("sigma", r"$\sigma$", 4.5, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 3, 1, scale=1.25, observed=True))
pgm.add_edge("alpha_prior", "alpha")
pgm.add_edge("beta_prior", "beta")
pgm.add_edge("sigma_prior", "sigma")
pgm.add_edge("sigma", "y_i")
pgm.add_edge("alpha", "y_i")
pgm.add_edge("beta", "y_i")
pgm.add_plate(daft.Plate([2.3, 0.1, 1.4, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
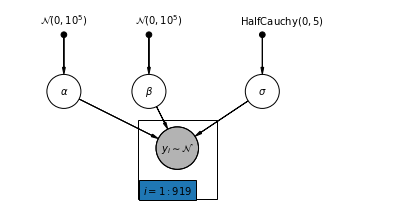
Aşağıda, Hamiltonian Monte Carlo'yu kullanarak tam havuzlama modelini uyguluyoruz.
@tf.function
def affine(x, kernel_diag, bias=tf.zeros([])):
"""`kernel_diag * x + bias` with broadcasting."""
kernel_diag = tf.ones_like(x) * kernel_diag
bias = tf.ones_like(x) * bias
return x * kernel_diag + bias
def pooled_model(floor):
"""Creates a joint distribution representing our generative process."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # alpha
tfd.Normal(loc=0., scale=1e5), # beta
tfd.HalfCauchy(loc=0., scale=5), # sigma
lambda s, b1, b0: tfd.MultivariateNormalDiag( # y
loc=affine(floor, b1[..., tf.newaxis], b0[..., tf.newaxis]),
scale_identity_multiplier=s)
])
@tf.function
def pooled_log_prob(alpha, beta, sigma):
"""Computes `joint_log_prob` pinned at `log_radon`."""
return pooled_model(floor).log_prob([alpha, beta, sigma, log_radon])
@tf.function
def sample_pooled(num_chains, num_results, num_burnin_steps, num_observations):
"""Samples from the pooled model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=pooled_log_prob,
num_leapfrog_steps=10,
step_size=0.005)
initial_state = [
tf.zeros([num_chains], name='init_alpha'),
tf.zeros([num_chains], name='init_beta'),
tf.ones([num_chains], name='init_sigma')
]
# Constrain `sigma` to the positive real axis. Other variables are
# unconstrained.
unconstraining_bijectors = [
tfb.Identity(), # alpha
tfb.Identity(), # beta
tfb.Exp() # sigma
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
PooledModel = collections.namedtuple('PooledModel', ['alpha', 'beta', 'sigma'])
samples, acceptance_probs = sample_pooled(
num_chains=4,
num_results=1000,
num_burnin_steps=1000,
num_observations=num_observations)
print('Acceptance Probabilities for each chain: ', acceptance_probs.numpy())
pooled_samples = PooledModel._make(samples)
Acceptance Probabilities for each chain: [0.997 0.99 0.997 0.995]
for var, var_samples in pooled_samples._asdict().items():
print('R-hat for ', var, ':\t',
tfp.mcmc.potential_scale_reduction(var_samples).numpy())
R-hat for alpha : 1.0046891 R-hat for beta : 1.0128309 R-hat for sigma : 1.0010641
def reduce_samples(var_samples, reduce_fn):
"""Reduces across leading two dims using reduce_fn."""
# Collapse the first two dimensions, typically (num_chains, num_samples), and
# compute np.mean or np.std along the remaining axis.
if isinstance(var_samples, tf.Tensor):
var_samples = var_samples.numpy() # convert to numpy array
var_samples = np.reshape(var_samples, (-1,) + var_samples.shape[2:])
return np.apply_along_axis(reduce_fn, axis=0, arr=var_samples)
sample_mean = lambda samples : reduce_samples(samples, np.mean)
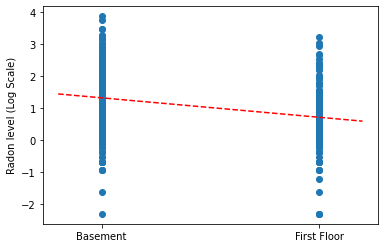
Tam havuzlama modeli için eğim ve kesişim nokta tahminlerini çizin.
LinearEstimates = collections.namedtuple('LinearEstimates',
['intercept', 'slope'])
pooled_estimate = LinearEstimates(
intercept=sample_mean(pooled_samples.alpha),
slope=sample_mean(pooled_samples.beta)
)
plt.scatter(radon.floor, radon.log_radon)
xvals = np.linspace(-0.2, 1.2)
plt.ylabel('Radon level (Log Scale)')
plt.xticks([0, 1], ['Basement', 'First Floor'])
plt.plot(xvals, pooled_estimate.intercept + pooled_estimate.slope * xvals, 'r--')
plt.show()
Örneklenen değişkenlerin izlerini çizmek için yardımcı fonksiyon.
def plot_traces(var_name, samples, num_chains):
if isinstance(samples, tf.Tensor):
samples = samples.numpy() # convert to numpy array
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
axes[0].plot(samples[:, chain], alpha=0.7)
axes[0].title.set_text("'{}' trace".format(var_name))
sns.kdeplot(samples[:, chain], ax=axes[1], shade=False)
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
axes[1].set_xlabel(var_name)
plt.show()
for var, var_samples in pooled_samples._asdict().items():
plot_traces(var, samples=var_samples, num_chains=4)



Daha sonra, havuzlanmamış modelde her ilçe için radon seviyelerini tahmin ediyoruz.
4.2 Havuzlanmamış Model
pgm = daft.PGM([7, 3.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"alpha_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
3,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"beta_prior",
r"$\mathcal{N}(0, 10^5)$",
2.5,
3,
fixed=True,
offset=(10, 5)))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4.5,
3,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("alpha", r"$\alpha$", 1, 2))
pgm.add_node(daft.Node("beta", r"$\beta$", 2.5, 2))
pgm.add_node(daft.Node("sigma", r"$\sigma$", 4.5, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 3, 1, scale=1.25, observed=True))
pgm.add_edge("alpha_prior", "alpha")
pgm.add_edge("beta_prior", "beta")
pgm.add_edge("sigma_prior", "sigma")
pgm.add_edge("sigma", "y_i")
pgm.add_edge("alpha", "y_i")
pgm.add_edge("beta", "y_i")
pgm.add_plate(daft.Plate([0.3, 1.1, 1.4, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([2.3, 0.1, 1.4, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
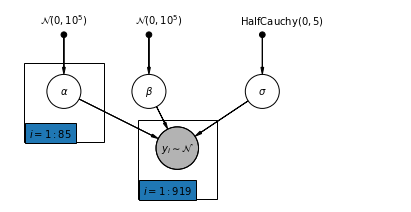
def unpooled_model(floor, county):
"""Creates a joint distribution for the unpooled model."""
return tfd.JointDistributionSequential([
tfd.MultivariateNormalDiag( # alpha
loc=tf.zeros([num_counties]), scale_identity_multiplier=1e5),
tfd.Normal(loc=0., scale=1e5), # beta
tfd.HalfCauchy(loc=0., scale=5), # sigma
lambda s, b1, b0: tfd.MultivariateNormalDiag( # y
loc=affine(
floor, b1[..., tf.newaxis], tf.gather(b0, county, axis=-1)),
scale_identity_multiplier=s)
])
@tf.function
def unpooled_log_prob(beta0, beta1, sigma):
"""Computes `joint_log_prob` pinned at `log_radon`."""
return (
unpooled_model(floor, county).log_prob([beta0, beta1, sigma, log_radon]))
@tf.function
def sample_unpooled(num_chains, num_results, num_burnin_steps):
"""Samples from the unpooled model."""
# Initialize the HMC transition kernel.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unpooled_log_prob,
num_leapfrog_steps=10,
step_size=0.025)
initial_state = [
tf.zeros([num_chains, num_counties], name='init_beta0'),
tf.zeros([num_chains], name='init_beta1'),
tf.ones([num_chains], name='init_sigma')
]
# Contrain `sigma` to the positive real axis. Other variables are
# unconstrained.
unconstraining_bijectors = [
tfb.Identity(), # alpha
tfb.Identity(), # beta
tfb.Exp() # sigma
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
UnpooledModel = collections.namedtuple('UnpooledModel',
['alpha', 'beta', 'sigma'])
samples, acceptance_probs = sample_unpooled(
num_chains=4, num_results=1000, num_burnin_steps=1000)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
unpooled_samples = UnpooledModel._make(samples)
print('R-hat for beta:',
tfp.mcmc.potential_scale_reduction(unpooled_samples.beta).numpy())
print('R-hat for sigma:',
tfp.mcmc.potential_scale_reduction(unpooled_samples.sigma).numpy())
Acceptance Probabilities: [0.892 0.897 0.911 0.91 ] R-hat for beta: 1.0079623 R-hat for sigma: 1.0059084
plot_traces(var_name='beta', samples=unpooled_samples.beta, num_chains=4)
plot_traces(var_name='sigma', samples=unpooled_samples.sigma, num_chains=4)


Burada, her zincir için %95 güvenilir aralıklarla birlikte kesişim için havuza alınmamış ilçe beklenen değerleri verilmiştir. Ayrıca her ilçenin tahmini için R-hat değerini de rapor ederiz.
Orman arazileri için fayda fonksiyonu.
def forest_plot(num_chains, num_vars, var_name, var_labels, samples):
fig, axes = plt.subplots(
1, 2, figsize=(12, 15), sharey=True, gridspec_kw={'width_ratios': [3, 1]})
for var_idx in range(num_vars):
values = samples[..., var_idx]
rhat = tfp.mcmc.diagnostic.potential_scale_reduction(values).numpy()
meds = np.median(values, axis=-2)
los = np.percentile(values, 5, axis=-2)
his = np.percentile(values, 95, axis=-2)
for i in range(num_chains):
height = 0.1 + 0.3 * var_idx + 0.05 * i
axes[0].plot([los[i], his[i]], [height, height], 'C0-', lw=2, alpha=0.5)
axes[0].plot([meds[i]], [height], 'C0o', ms=1.5)
axes[1].plot([rhat], [height], 'C0o', ms=4)
axes[0].set_yticks(np.linspace(0.2, 0.3, num_vars))
axes[0].set_ylim(0, 26)
axes[0].grid(which='both')
axes[0].invert_yaxis()
axes[0].set_yticklabels(var_labels)
axes[0].xaxis.set_label_position('top')
axes[0].set(xlabel='95% Credible Intervals for {}'.format(var_name))
axes[1].set_xticks([1, 2])
axes[1].set_xlim(0.95, 2.05)
axes[1].grid(which='both')
axes[1].set(xlabel='R-hat')
axes[1].xaxis.set_label_position('top')
plt.show()
forest_plot(
num_chains=4,
num_vars=num_counties,
var_name='alpha',
var_labels=county_name,
samples=unpooled_samples.alpha.numpy())

Yüksek radon seviyelerine sahip ilçeleri belirlemek için sıralı tahminleri çizebiliriz:
unpooled_intercepts = reduce_samples(unpooled_samples.alpha, np.mean)
unpooled_intercepts_se = reduce_samples(unpooled_samples.alpha, np.std)
def plot_ordered_estimates():
means = pd.Series(unpooled_intercepts, index=county_name)
std_errors = pd.Series(unpooled_intercepts_se, index=county_name)
order = means.sort_values().index
plt.plot(range(num_counties), means[order], '.')
for i, m, se in zip(range(num_counties), means[order], std_errors[order]):
plt.plot([i, i], [m - se, m + se], 'C0-')
plt.xlabel('Ordered county')
plt.ylabel('Radon estimate')
plt.show()
plot_ordered_estimates()
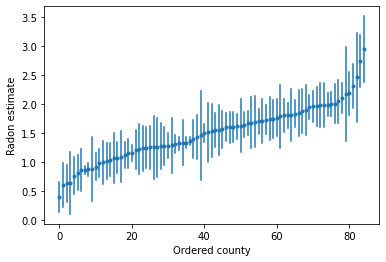
Örnek bir ilçe kümesi için tahminleri çizmek için fayda işlevi.
def plot_estimates(linear_estimates, labels, sample_counties):
fig, axes = plt.subplots(2, 4, figsize=(12, 6), sharey=True, sharex=True)
axes = axes.ravel()
intercepts_indexed = []
slopes_indexed = []
for intercepts, slopes in linear_estimates:
intercepts_indexed.append(pd.Series(intercepts, index=county_name))
slopes_indexed.append(pd.Series(slopes, index=county_name))
markers = ['-', 'r--', 'k:']
sample_county_codes = [county_name.index(c) for c in sample_counties]
for i, c in enumerate(sample_county_codes):
y = radon.log_radon[radon.county == c]
x = radon.floor[radon.county == c]
axes[i].scatter(
x + np.random.randn(len(x)) * 0.01, y, alpha=0.4, label='Log Radon')
# Plot both models and data
xvals = np.linspace(-0.2, 1.2)
for k in range(len(intercepts_indexed)):
axes[i].plot(
xvals,
intercepts_indexed[k][c] + slopes_indexed[k][c] * xvals,
markers[k],
label=labels[k])
axes[i].set_xticks([0, 1])
axes[i].set_xticklabels(['Basement', 'First Floor'])
axes[i].set_ylim(-1, 3)
axes[i].set_title(sample_counties[i])
if not i % 2:
axes[i].set_ylabel('Log Radon level')
axes[3].legend(bbox_to_anchor=(1.05, 0.9), borderaxespad=0.)
plt.show()
Burada, bir dizi örneklem boyutunu temsil eden bir ilçe alt kümesi için havuzlanmış ve havuzlanmamış tahminler arasındaki görsel karşılaştırmalar verilmiştir.
unpooled_estimates = LinearEstimates(
sample_mean(unpooled_samples.alpha),
sample_mean(unpooled_samples.beta)
)
sample_counties = ('Lac Qui Parle', 'Aitkin', 'Koochiching', 'Douglas', 'Clay',
'Stearns', 'Ramsey', 'St Louis')
plot_estimates(
linear_estimates=[unpooled_estimates, pooled_estimate],
labels=['Unpooled Estimates', 'Pooled Estimates'],
sample_counties=sample_counties)
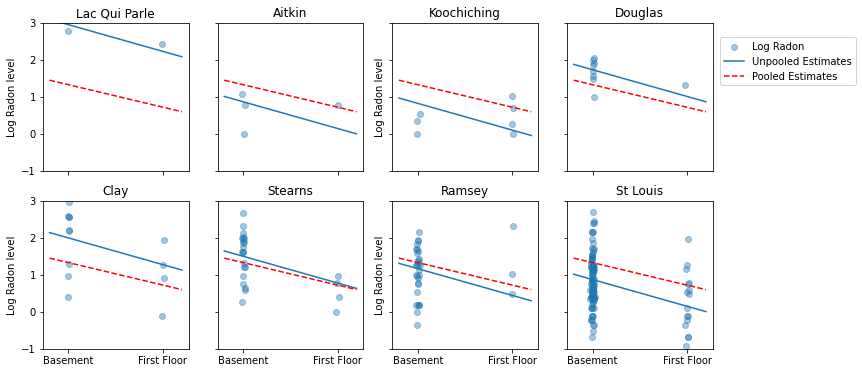
Bu modellerin hiçbiri tatmin edici değil:
- yüksek radonlu ilçeleri belirlemeye çalışıyorsak, havuzlama yararlı değildir.
- birkaç gözlem kullanan modeller tarafından üretilen aşırı havuzlanmamış tahminlere güvenmiyoruz.
5 Çok düzeyli ve Hiyerarşik modeller
Verilerimizi bir araya getirdiğimizde, farklı ilçelerden farklı veri noktalarının geldiği bilgisini kaybederiz. Her birinin bu araçlar radon -seviye gözlem, aynı olasılık dağılımından örneklenir. Böyle bir model, bir grup (örneğin bir ilçe) içinde var olan örnekleme birimindeki herhangi bir varyasyonu öğrenmede başarısız olur. Yalnızca örnekleme varyansını hesaba katar.
mpl.rc("font", size=18)
pgm = daft.PGM([13.6, 2.2], origin=[1.15, 1.0], node_ec="none")
pgm.add_node(daft.Node("parameter", r"parameter", 2.0, 3))
pgm.add_node(daft.Node("observations", r"observations", 2.0, 2))
pgm.add_node(daft.Node("theta", r"$\theta$", 5.5, 3))
pgm.add_node(daft.Node("y_0", r"$y_0$", 4, 2))
pgm.add_node(daft.Node("y_1", r"$y_1$", 5, 2))
pgm.add_node(daft.Node("dots", r"$\cdots$", 6, 2))
pgm.add_node(daft.Node("y_k", r"$y_k$", 7, 2))
pgm.add_edge("theta", "y_0")
pgm.add_edge("theta", "y_1")
pgm.add_edge("theta", "y_k")
pgm.render()
plt.show()
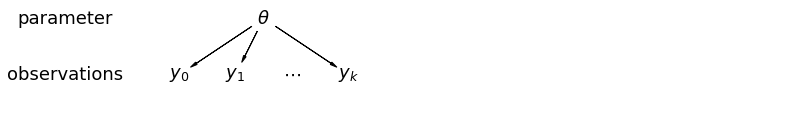
Havuzlanmamış verileri analiz ettiğimizde, bunların ayrı modellerden bağımsız olarak örneklendiklerini ima ederiz. Birleştirilmiş durumun tam tersi olan bu yaklaşım, örnekleme birimleri arasındaki farklılıkların bunları birleştirmek için çok büyük olduğunu iddia eder:
mpl.rc("font", size=18)
pgm = daft.PGM([13.6, 2.2], origin=[1.15, 1.0], node_ec="none")
pgm.add_node(daft.Node("parameter", r"parameter", 2.0, 3))
pgm.add_node(daft.Node("observations", r"observations", 2.0, 2))
pgm.add_node(daft.Node("theta_0", r"$\theta_0$", 4, 3))
pgm.add_node(daft.Node("theta_1", r"$\theta_1$", 5, 3))
pgm.add_node(daft.Node("theta_dots", r"$\cdots$", 6, 3))
pgm.add_node(daft.Node("theta_k", r"$\theta_k$", 7, 3))
pgm.add_node(daft.Node("y_0", r"$y_0$", 4, 2))
pgm.add_node(daft.Node("y_1", r"$y_1$", 5, 2))
pgm.add_node(daft.Node("y_dots", r"$\cdots$", 6, 2))
pgm.add_node(daft.Node("y_k", r"$y_k$", 7, 2))
pgm.add_edge("theta_0", "y_0")
pgm.add_edge("theta_1", "y_1")
pgm.add_edge("theta_k", "y_k")
pgm.render()
plt.show()
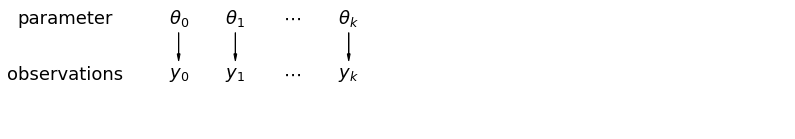
Hiyerarşik bir modelde parametreler, parametrelerin popülasyon dağılımından bir örnek olarak görülür. Bu nedenle, onları ne tamamen farklı ne de tamamen aynı olarak görüyoruz. Bu kısmi havuzu olarak bilinir.
mpl.rc("font", size=18)
pgm = daft.PGM([13.6, 3.4], origin=[1.15, 1.0], node_ec="none")
pgm.add_node(daft.Node("model", r"model", 2.0, 4))
pgm.add_node(daft.Node("parameter", r"parameter", 2.0, 3))
pgm.add_node(daft.Node("observations", r"observations", 2.0, 2))
pgm.add_node(daft.Node("mu_sigma", r"$\mu,\sigma^2$", 5.5, 4))
pgm.add_node(daft.Node("theta_0", r"$\theta_0$", 4, 3))
pgm.add_node(daft.Node("theta_1", r"$\theta_1$", 5, 3))
pgm.add_node(daft.Node("theta_dots", r"$\cdots$", 6, 3))
pgm.add_node(daft.Node("theta_k", r"$\theta_k$", 7, 3))
pgm.add_node(daft.Node("y_0", r"$y_0$", 4, 2))
pgm.add_node(daft.Node("y_1", r"$y_1$", 5, 2))
pgm.add_node(daft.Node("y_dots", r"$\cdots$", 6, 2))
pgm.add_node(daft.Node("y_k", r"$y_k$", 7, 2))
pgm.add_edge("mu_sigma", "theta_0")
pgm.add_edge("mu_sigma", "theta_1")
pgm.add_edge("mu_sigma", "theta_k")
pgm.add_edge("theta_0", "y_0")
pgm.add_edge("theta_1", "y_1")
pgm.add_edge("theta_k", "y_k")
pgm.render()
plt.show()
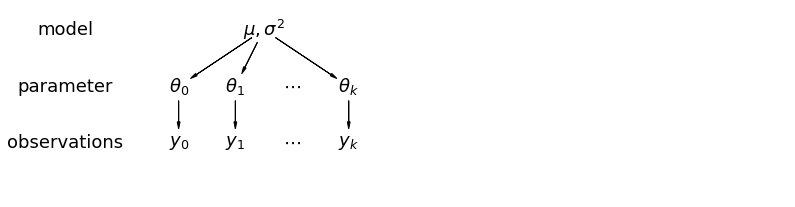
5.1 Kısmi Havuzlama
Ev radon veri seti için en basit kısmi havuzlama modeli, grup veya bireysel düzeyde herhangi bir tahmin edici olmaksızın radon seviyelerini basitçe tahmin eden bir modeldir. Bireysel seviye tahmincisine bir örnek, veri noktasının bodrum katından mı yoksa birinci kattan mı olduğudur. Grup düzeyinde bir öngörücü, ilçe genelindeki ortalama uranyum seviyeleri olabilir.
Kısmi bir havuzlama modeli, havuzlanmış ve havuzlanmamış uç noktalar arasında bir uzlaşmayı, havuza alınmamış ilçe tahminlerinin ve havuzlanmış tahminlerin yaklaşık olarak ağırlıklı bir ortalamasını (örnek boyutuna dayalı olarak) temsil eder.
Let \(\hat{\alpha}_j\) ilçe tahmini log radon seviyesi olmak \(j\). Bu sadece bir kesişme; şimdilik yokuşları görmezden geliyoruz. \(n_j\) ilçe gelen gözlem sayısıdır \(j\). \(\sigma_{\alpha}\) ve \(\sigma_y\) parametresi olan varyans ve sırasıyla örnekleme varyans vardır. O zaman kısmi bir havuzlama modeli şunları önerebilir:
\[\hat{\alpha}_j \approx \frac{(n_j/\sigma_y^2)\bar{y}_j + (1/\sigma_{\alpha}^2)\bar{y} }{(n_j/\sigma_y^2) + (1/\sigma_{\alpha}^2)}\]
Kısmi havuzlama kullanırken aşağıdakileri bekliyoruz:
- Daha küçük örneklem boyutlarına sahip ilçeler için tahminler, eyalet çapındaki ortalamaya doğru küçülecektir.
- Daha büyük örneklem boyutlarına sahip ilçeler için tahminler, havuzlanmamış ilçe tahminlerine daha yakın olacaktır.
mpl.rc("font", size=12)
pgm = daft.PGM([7, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"mu_a_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
3,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4,
3,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("mu_a", r"$\mu_a$", 1, 3))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{N}$", 2, 2, scale=1.25))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 3.25, 1, scale=1.25, observed=True))
pgm.add_edge("mu_a_prior", "mu_a")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("mu_a", "a")
pgm.add_edge("sigma_a", "a")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_plate(daft.Plate([1.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([2.65, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
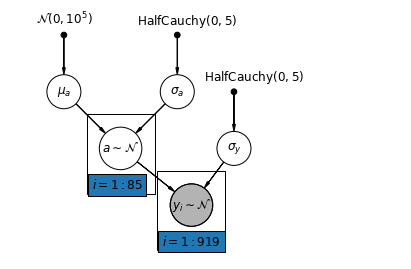
def partial_pooling_model(county):
"""Creates a joint distribution for the partial pooling model."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # mu_a
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a, mu_a: tfd.MultivariateNormalDiag( # a
loc=mu_a[..., tf.newaxis] * tf.ones([num_counties])[tf.newaxis, ...],
scale_identity_multiplier=sigma_a),
tfd.HalfCauchy(loc=0., scale=5), # sigma_y
lambda sigma_y, a: tfd.MultivariateNormalDiag( # y
loc=tf.gather(a, county, axis=-1),
scale_identity_multiplier=sigma_y)
])
@tf.function
def partial_pooling_log_prob(mu_a, sigma_a, a, sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return partial_pooling_model(county).log_prob(
[mu_a, sigma_a, a, sigma_y, log_radon])
@tf.function
def sample_partial_pooling(num_chains, num_results, num_burnin_steps):
"""Samples from the partial pooling model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=partial_pooling_log_prob,
num_leapfrog_steps=10,
step_size=0.01)
initial_state = [
tf.zeros([num_chains], name='init_mu_a'),
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='init_a'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Identity(), # mu_a
tfb.Exp(), # sigma_a
tfb.Identity(), # a
tfb.Exp() # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
PartialPoolingModel = collections.namedtuple(
'PartialPoolingModel', ['mu_a', 'sigma_a', 'a', 'sigma_y'])
samples, acceptance_probs = sample_partial_pooling(
num_chains=4, num_results=1000, num_burnin_steps=1000)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
partial_pooling_samples = PartialPoolingModel._make(samples)
Acceptance Probabilities: [0.989 0.977 0.988 0.985]
for var in ['mu_a', 'sigma_a', 'sigma_y']:
print(
'R-hat for ', var, '\t:',
tfp.mcmc.potential_scale_reduction(getattr(partial_pooling_samples,
var)).numpy())
R-hat for mu_a : 1.0216417 R-hat for sigma_a : 1.0224565 R-hat for sigma_y : 1.0016255
partial_pooling_intercepts = reduce_samples(
partial_pooling_samples.a.numpy(), np.mean)
partial_pooling_intercepts_se = reduce_samples(
partial_pooling_samples.a.numpy(), np.std)
def plot_unpooled_vs_partial_pooling_estimates():
fig, axes = plt.subplots(1, 2, figsize=(14, 6), sharex=True, sharey=True)
# Order counties by number of observations (and add some jitter).
num_obs_per_county = (
radon.groupby('county')['idnum'].count().values.astype(np.float32))
num_obs_per_county += np.random.normal(scale=0.5, size=num_counties)
intercepts_list = [unpooled_intercepts, partial_pooling_intercepts]
intercepts_se_list = [unpooled_intercepts_se, partial_pooling_intercepts_se]
for ax, means, std_errors in zip(axes, intercepts_list, intercepts_se_list):
ax.plot(num_obs_per_county, means, 'C0.')
for n, m, se in zip(num_obs_per_county, means, std_errors):
ax.plot([n, n], [m - se, m + se], 'C1-', alpha=.5)
for ax in axes:
ax.set_xscale('log')
ax.set_xlabel('No. of Observations Per County')
ax.set_xlim(1, 100)
ax.set_ylabel('Log Radon Estimate (with Standard Error)')
ax.set_ylim(0, 3)
ax.hlines(partial_pooling_intercepts.mean(), .9, 125, 'k', '--', alpha=.5)
axes[0].set_title('Unpooled Estimates')
axes[1].set_title('Partially Pooled Estimates')
plot_unpooled_vs_partial_pooling_estimates()
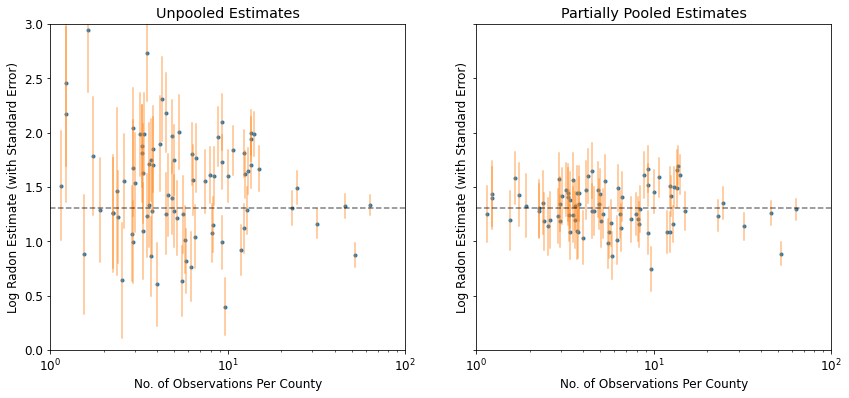
Özellikle daha küçük örneklem boyutlarında, havuzlanmamış ve kısmen havuzlanmış tahminler arasındaki farka dikkat edin. İlki hem daha aşırı hem de daha kesin değil.
5.2 Değişen Kesişmeler
Şimdi, kesişmelerin rastgele bir etkiye göre ilçe genelinde değişmesine izin veren daha karmaşık bir model düşünüyoruz.
\(y_i = \alpha_{j[i]} + \beta x_{i} + \epsilon_i\) burada\(\epsilon_i \sim N(0, \sigma_y^2)\) ve ara rastgele etki:
\[\alpha_{j[i]} \sim N(\mu_{\alpha}, \sigma_{\alpha}^2)\]
Eğim \(\beta\)gözlem ölçümü (bodrum veya birinci kat) yere göre değişir sağlar, yine de farklı il arasında paylaşılan bir sabit etkisidir.
Unpooling modelle olarak, her ilçe için ayrı kesişim set değil, az veri olan ilçede daha makul çıkarım için izin iller arasında her ilçe, düzeyli modelleme hisseleri mukavemet için ayrı en küçük kareler regresyon modelleri uydurma daha.
mpl.rc("font", size=12)
pgm = daft.PGM([7, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"mu_a_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
3,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(
daft.Node(
"b_prior",
r"$\mathcal{N}(0, 10^5)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("b", r"$b$", 4, 2.5))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
6,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("mu_a", r"$\mu_a$", 1, 3))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{N}$", 2, 2, scale=1.25))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 6, 2.5))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("mu_a_prior", "mu_a")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("mu_a", "a")
pgm.add_edge("b_prior", "b")
pgm.add_edge("sigma_a", "a")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([1.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
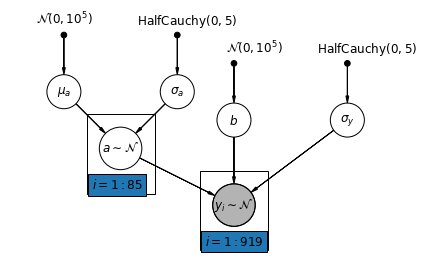
def varying_intercept_model(floor, county):
"""Creates a joint distribution for the varying intercept model."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # mu_a
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a, mu_a: tfd.MultivariateNormalDiag( # a
loc=affine(tf.ones([num_counties]), mu_a[..., tf.newaxis]),
scale_identity_multiplier=sigma_a),
tfd.Normal(loc=0., scale=1e5), # b
tfd.HalfCauchy(loc=0., scale=5), # sigma_y
lambda sigma_y, b, a: tfd.MultivariateNormalDiag( # y
loc=affine(floor, b[..., tf.newaxis], tf.gather(a, county, axis=-1)),
scale_identity_multiplier=sigma_y)
])
def varying_intercept_log_prob(mu_a, sigma_a, a, b, sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return varying_intercept_model(floor, county).log_prob(
[mu_a, sigma_a, a, b, sigma_y, log_radon])
@tf.function
def sample_varying_intercepts(num_chains, num_results, num_burnin_steps):
"""Samples from the varying intercepts model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=varying_intercept_log_prob,
num_leapfrog_steps=10,
step_size=0.01)
initial_state = [
tf.zeros([num_chains], name='init_mu_a'),
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='init_a'),
tf.zeros([num_chains], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Identity(), # mu_a
tfb.Exp(), # sigma_a
tfb.Identity(), # a
tfb.Identity(), # b
tfb.Exp() # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
VaryingInterceptsModel = collections.namedtuple(
'VaryingInterceptsModel', ['mu_a', 'sigma_a', 'a', 'b', 'sigma_y'])
samples, acceptance_probs = sample_varying_intercepts(
num_chains=4, num_results=1000, num_burnin_steps=1000)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
varying_intercepts_samples = VaryingInterceptsModel._make(samples)
Acceptance Probabilities: [0.978 0.987 0.982 0.984]
for var in ['mu_a', 'sigma_a', 'b', 'sigma_y']:
print(
'R-hat for ', var, ': ',
tfp.mcmc.potential_scale_reduction(
getattr(varying_intercepts_samples, var)).numpy())
R-hat for mu_a : 1.1099764 R-hat for sigma_a : 1.1058794 R-hat for b : 1.0448593 R-hat for sigma_y : 1.0019052
varying_intercepts_estimates = LinearEstimates(
sample_mean(varying_intercepts_samples.a),
sample_mean(varying_intercepts_samples.b))
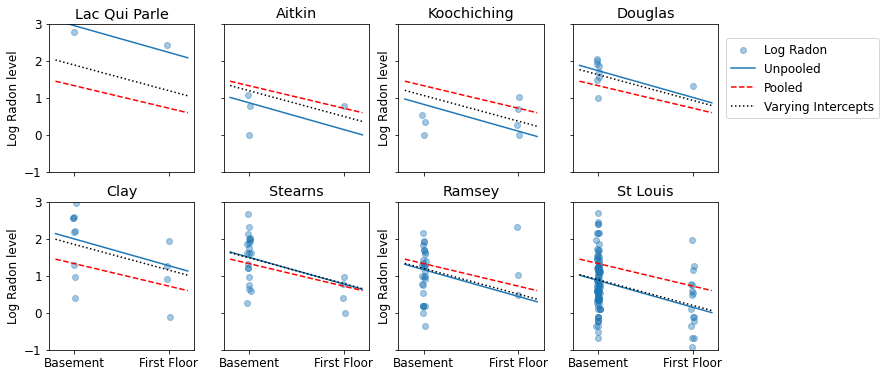
sample_counties = ('Lac Qui Parle', 'Aitkin', 'Koochiching', 'Douglas', 'Clay',
'Stearns', 'Ramsey', 'St Louis')
plot_estimates(
linear_estimates=[
unpooled_estimates, pooled_estimate, varying_intercepts_estimates
],
labels=['Unpooled', 'Pooled', 'Varying Intercepts'],
sample_counties=sample_counties)
def plot_posterior(var_name, var_samples):
if isinstance(var_samples, tf.Tensor):
var_samples = var_samples.numpy() # convert to numpy array
fig = plt.figure(figsize=(10, 3))
ax = fig.add_subplot(111)
ax.hist(var_samples.flatten(), bins=40, edgecolor='white')
sample_mean = var_samples.mean()
ax.text(
sample_mean,
100,
'mean={:.3f}'.format(sample_mean),
color='white',
fontsize=12)
ax.set_xlabel('posterior of ' + var_name)
plt.show()
plot_posterior('b', varying_intercepts_samples.b)
plot_posterior('sigma_a', varying_intercepts_samples.sigma_a)
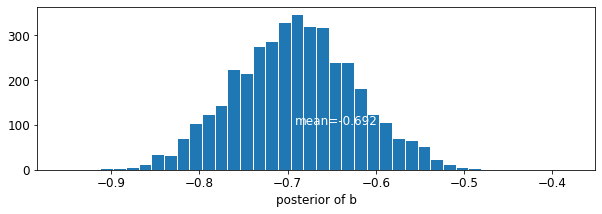
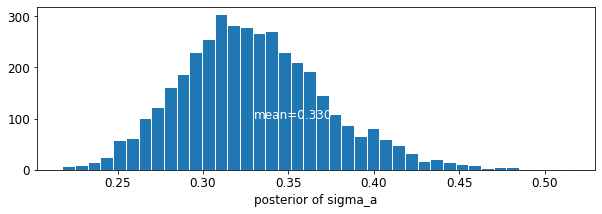
Zemin katsayısı için tahmini yaklaşık yarısı (yaklaşık sahip olan bodrum olmayan ev olarak yorumlanabilir -0.69 olduğu\(\exp(-0.69) = 0.50\)il için hesaplandıktan sonra,) bodrum olan radon seviyeleri.
for var in ['b']:
var_samples = getattr(varying_intercepts_samples, var)
mean = var_samples.numpy().mean()
std = var_samples.numpy().std()
r_hat = tfp.mcmc.potential_scale_reduction(var_samples).numpy()
n_eff = tfp.mcmc.effective_sample_size(var_samples).numpy().sum()
print('var: ', var, ' mean: ', mean, ' std: ', std, ' n_eff: ', n_eff,
' r_hat: ', r_hat)
var: b mean: -0.6972574 std: 0.06966117 n_eff: 397.94327 r_hat: 1.0448593
def plot_intercepts_and_slopes(linear_estimates, title):
xvals = np.arange(2)
intercepts = np.ones([num_counties]) * linear_estimates.intercept
slopes = np.ones([num_counties]) * linear_estimates.slope
fig, ax = plt.subplots()
for c in range(num_counties):
ax.plot(xvals, intercepts[c] + slopes[c] * xvals, 'bo-', alpha=0.4)
plt.xlim(-0.2, 1.2)
ax.set_xticks([0, 1])
ax.set_xticklabels(['Basement', 'First Floor'])
ax.set_ylabel('Log Radon level')
plt.title(title)
plt.show()
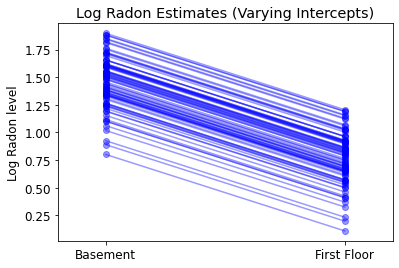
plot_intercepts_and_slopes(varying_intercepts_estimates,
'Log Radon Estimates (Varying Intercepts)')
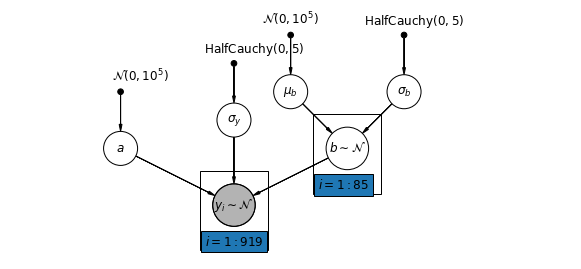
5.3 Değişken Eğimler
Alternatif olarak, ölçüm konumunun (bodrum veya birinci kat) radon okumasını nasıl etkilediğine göre ilçelerin değişmesine izin veren bir model önerebiliriz. Bu durumda kesişme \(\alpha\) ilçeleri arasında paylaşılır.
\[y_i = \alpha + \beta_{j[i]} x_{i} + \epsilon_i\]
mpl.rc("font", size=12)
pgm = daft.PGM([10, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"mu_b_prior",
r"$\mathcal{N}(0, 10^5)$",
3.2,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"a_prior", r"$\mathcal{N}(0, 10^5)$", 2, 3, fixed=True, offset=(20, 5)))
pgm.add_node(daft.Node("a", r"$a$", 2, 2))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2.5))
pgm.add_node(
daft.Node(
"mu_b_prior",
r"$\mathcal{N}(0, 10^5)$",
5,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_b_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
7,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("mu_b", r"$\mu_b$", 5, 3))
pgm.add_node(daft.Node("sigma_b", r"$\sigma_b$", 7, 3))
pgm.add_node(daft.Node("b", r"$b \sim \mathcal{N}$", 6, 2, scale=1.25))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("a_prior", "a")
pgm.add_edge("mu_b_prior", "mu_b")
pgm.add_edge("sigma_b_prior", "sigma_b")
pgm.add_edge("mu_b", "b")
pgm.add_edge("sigma_b", "b")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([5.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
def varying_slopes_model(floor, county):
"""Creates a joint distribution for the varying slopes model."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # mu_b
tfd.HalfCauchy(loc=0., scale=5), # sigma_b
tfd.Normal(loc=0., scale=1e5), # a
lambda _, sigma_b, mu_b: tfd.MultivariateNormalDiag( # b
loc=affine(tf.ones([num_counties]), mu_b[..., tf.newaxis]),
scale_identity_multiplier=sigma_b),
tfd.HalfCauchy(loc=0., scale=5), # sigma_y
lambda sigma_y, b, a: tfd.MultivariateNormalDiag( # y
loc=affine(floor, tf.gather(b, county, axis=-1), a[..., tf.newaxis]),
scale_identity_multiplier=sigma_y)
])
def varying_slopes_log_prob(mu_b, sigma_b, a, b, sigma_y):
return varying_slopes_model(floor, county).log_prob(
[mu_b, sigma_b, a, b, sigma_y, log_radon])
@tf.function
def sample_varying_slopes(num_chains, num_results, num_burnin_steps):
"""Samples from the varying slopes model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=varying_slopes_log_prob,
num_leapfrog_steps=25,
step_size=0.01)
initial_state = [
tf.zeros([num_chains], name='init_mu_b'),
tf.ones([num_chains], name='init_sigma_b'),
tf.zeros([num_chains], name='init_a'),
tf.zeros([num_chains, num_counties], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Identity(), # mu_b
tfb.Exp(), # sigma_b
tfb.Identity(), # a
tfb.Identity(), # b
tfb.Exp() # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
VaryingSlopesModel = collections.namedtuple(
'VaryingSlopesModel', ['mu_b', 'sigma_b', 'a', 'b', 'sigma_y'])
samples, acceptance_probs = sample_varying_slopes(
num_chains=4, num_results=1000, num_burnin_steps=1000)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
varying_slopes_samples = VaryingSlopesModel._make(samples)
Acceptance Probabilities: [0.979 0.984 0.977 0.984]
for var in ['mu_b', 'sigma_b', 'a', 'sigma_y']:
print(
'R-hat for ', var, '\t: ',
tfp.mcmc.potential_scale_reduction(getattr(varying_slopes_samples,
var)).numpy())
R-hat for mu_b : 1.0770341 R-hat for sigma_b : 1.0634488 R-hat for a : 1.0133665 R-hat for sigma_y : 1.0011941
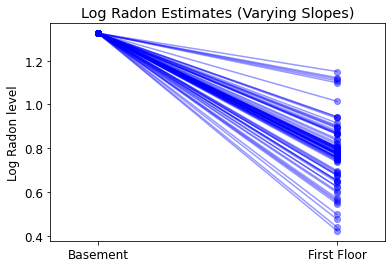
varying_slopes_estimates = LinearEstimates(
sample_mean(varying_slopes_samples.a),
sample_mean(varying_slopes_samples.b))
plot_intercepts_and_slopes(varying_slopes_estimates,
'Log Radon Estimates (Varying Slopes)')
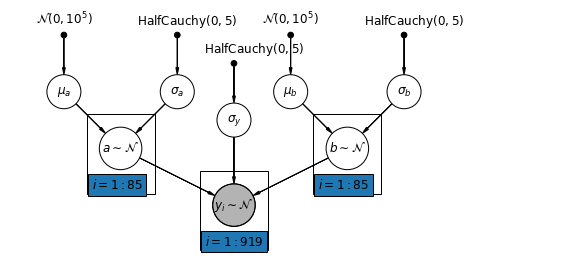
5.4 Değişen Kesişmeler ve Eğimler
En genel model, hem kesişim hem de eğimin ilçeye göre değişmesine izin verir:
\[y_i = \alpha_{j[i]} + \beta_{j[i]} x_{i} + \epsilon_i\]
mpl.rc("font", size=12)
pgm = daft.PGM([10, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"mu_a_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
3,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("mu_a", r"$\mu_a$", 1, 3))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{N}$", 2, 2, scale=1.25))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2.5))
pgm.add_node(
daft.Node(
"mu_b_prior",
r"$\mathcal{N}(0, 10^5)$",
5,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_b_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
7,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("mu_b", r"$\mu_b$", 5, 3))
pgm.add_node(daft.Node("sigma_b", r"$\sigma_b$", 7, 3))
pgm.add_node(daft.Node("b", r"$b \sim \mathcal{N}$", 6, 2, scale=1.25))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("mu_a_prior", "mu_a")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("mu_a", "a")
pgm.add_edge("sigma_a", "a")
pgm.add_edge("mu_b_prior", "mu_b")
pgm.add_edge("sigma_b_prior", "sigma_b")
pgm.add_edge("mu_b", "b")
pgm.add_edge("sigma_b", "b")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([1.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([5.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
def varying_intercepts_and_slopes_model(floor, county):
"""Creates a joint distribution for the varying slope model."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # mu_a
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
tfd.Normal(loc=0., scale=1e5), # mu_b
tfd.HalfCauchy(loc=0., scale=5), # sigma_b
lambda sigma_b, mu_b, sigma_a, mu_a: tfd.MultivariateNormalDiag( # a
loc=affine(tf.ones([num_counties]), mu_a[..., tf.newaxis]),
scale_identity_multiplier=sigma_a),
lambda _, sigma_b, mu_b: tfd.MultivariateNormalDiag( # b
loc=affine(tf.ones([num_counties]), mu_b[..., tf.newaxis]),
scale_identity_multiplier=sigma_b),
tfd.HalfCauchy(loc=0., scale=5), # sigma_y
lambda sigma_y, b, a: tfd.MultivariateNormalDiag( # y
loc=affine(floor, tf.gather(b, county, axis=-1),
tf.gather(a, county, axis=-1)),
scale_identity_multiplier=sigma_y)
])
@tf.function
def varying_intercepts_and_slopes_log_prob(mu_a, sigma_a, mu_b, sigma_b, a, b,
sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return varying_intercepts_and_slopes_model(floor, county).log_prob(
[mu_a, sigma_a, mu_b, sigma_b, a, b, sigma_y, log_radon])
@tf.function
def sample_varying_intercepts_and_slopes(num_chains, num_results,
num_burnin_steps):
"""Samples from the varying intercepts and slopes model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=varying_intercepts_and_slopes_log_prob,
num_leapfrog_steps=50,
step_size=0.01)
initial_state = [
tf.zeros([num_chains], name='init_mu_a'),
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains], name='init_mu_b'),
tf.ones([num_chains], name='init_sigma_b'),
tf.zeros([num_chains, num_counties], name='init_a'),
tf.zeros([num_chains, num_counties], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Identity(), # mu_a
tfb.Exp(), # sigma_a
tfb.Identity(), # mu_b
tfb.Exp(), # sigma_b
tfb.Identity(), # a
tfb.Identity(), # b
tfb.Exp() # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
VaryingInterceptsAndSlopesModel = collections.namedtuple(
'VaryingInterceptsAndSlopesModel',
['mu_a', 'sigma_a', 'mu_b', 'sigma_b', 'a', 'b', 'sigma_y'])
samples, acceptance_probs = sample_varying_intercepts_and_slopes(
num_chains=4, num_results=1000, num_burnin_steps=500)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
varying_intercepts_and_slopes_samples = VaryingInterceptsAndSlopesModel._make(
samples)
Acceptance Probabilities: [0.988 0.985 0.992 0.938]
for var in ['mu_a', 'sigma_a', 'mu_b', 'sigma_b']:
print(
'R-hat for ', var, '\t: ',
tfp.mcmc.potential_scale_reduction(
getattr(varying_intercepts_and_slopes_samples, var)).numpy())
R-hat for mu_a : 1.010764 R-hat for sigma_a : 1.0078123 R-hat for mu_b : 1.0279609 R-hat for sigma_b : 1.3165458
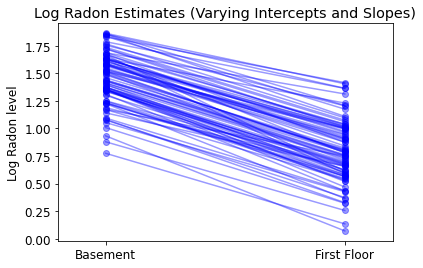
varying_intercepts_and_slopes_estimates = LinearEstimates(
sample_mean(varying_intercepts_and_slopes_samples.a),
sample_mean(varying_intercepts_and_slopes_samples.b))
plot_intercepts_and_slopes(
varying_intercepts_and_slopes_estimates,
'Log Radon Estimates (Varying Intercepts and Slopes)')
forest_plot(
num_chains=4,
num_vars=num_counties,
var_name='a',
var_labels=county_name,
samples=varying_intercepts_and_slopes_samples.a.numpy())
forest_plot(
num_chains=4,
num_vars=num_counties,
var_name='b',
var_labels=county_name,
samples=varying_intercepts_and_slopes_samples.b.numpy())


6 Grup Düzeyinde Tahminciler Ekleme
Çok düzeyli modellerin birincil gücü, aynı anda birden çok düzeydeki tahmin edicileri işleme yeteneğidir. Yukarıdaki değişken kesişim modelini ele alırsak:
\(y_i = \alpha_{j[i]} + \beta x_{i} + \epsilon_i\) biz yerine basit tesadüfi etki, beklenen radon değerindeki değişim açıklayan bir ilçe düzeyinde ortak değişken ile başka regresyon modeli belirtmek için olabilir. Burada, okuma ilçe uranyum kullanmak \(u_j\)radon düzeyi ile ilişkili olduğu düşünülmektedir:
\(\alpha_j = \gamma_0 + \gamma_1 u_j + \zeta_j\)\(\zeta_j \sim N(0, \sigma_{\alpha}^2)\) Böylece, artık bir ev düzey öngorücunun (zemin veya bodrum) yanı sıra bir ilçe düzeyinde öngorücunun (uranyum) dahil ediyor.
Modelin her ilçe için her iki gösterge değişkenine ve ayrıca ilçe düzeyinde bir ortak değişkene sahip olduğuna dikkat edin. Klasik regresyonda bu, doğrusallık ile sonuçlanır. Çok seviyeli bir modelde, grup seviyesindeki doğrusal modelin beklenen değerine doğru kesişen noktaların kısmi olarak birleştirilmesi bunu önler.
Grup düzeyinde haberciler grubu düzeyindeki varyasyonu azaltmak için hizmet\(\sigma_{\alpha}\). Bunun önemli bir anlamı, grup düzeyinde tahminin daha güçlü bir havuz oluşturmaya neden olmasıdır.
6.1 Hiyerarşik Kesişmeler modeli
mpl.rc("font", size=12)
pgm = daft.PGM([10, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"gamma_0_prior",
r"$\mathcal{N}(0, 10^5)$",
0.5,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"gamma_1_prior",
r"$\mathcal{N}(0, 10^5)$",
1.5,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("gamma_0", r"$\gamma_0$", 0.5, 3))
pgm.add_node(daft.Node("gamma_1", r"$\gamma_1$", 1.5, 3))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathcal{N}(0, 10^5)$",
3,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3.5))
pgm.add_node(daft.Node("eps_a", r"$eps_a$", 3, 2.5, scale=1.25))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{Det}$", 1.5, 1.2, scale=1.5))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{U}(0, 100)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2.5))
pgm.add_node(daft.Node("b_prior", r"$\mathcal{N}(0, 10^5)$", 5, 3, fixed=True))
pgm.add_node(daft.Node("b", r"$b$", 5, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("gamma_0_prior", "gamma_0")
pgm.add_edge("gamma_1_prior", "gamma_1")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("sigma_a", "eps_a")
pgm.add_edge("gamma_0", "a")
pgm.add_edge("gamma_1", "a")
pgm.add_edge("eps_a", "a")
pgm.add_edge("b_prior", "b")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([2.4, 1.7, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([0.9, 0.4, 1.2, 1.4], "$i = 1:919$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
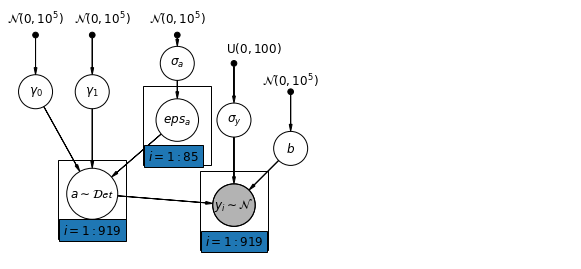
def hierarchical_intercepts_model(floor, county, log_uranium):
"""Creates a joint distribution for the varying slope model."""
return tfd.JointDistributionSequential([
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a: tfd.MultivariateNormalDiag( # eps_a
loc=tf.zeros([num_counties]),
scale_identity_multiplier=sigma_a),
tfd.Normal(loc=0., scale=1e5), # gamma_0
tfd.Normal(loc=0., scale=1e5), # gamma_1
tfd.Normal(loc=0., scale=1e5), # b
tfd.Uniform(low=0., high=100), # sigma_y
lambda sigma_y, b, gamma_1, gamma_0, eps_a: tfd.
MultivariateNormalDiag( # y
loc=affine(
floor, b[..., tf.newaxis],
affine(log_uranium, gamma_1[..., tf.newaxis],
gamma_0[..., tf.newaxis]) + tf.gather(eps_a, county, axis=-1)),
scale_identity_multiplier=sigma_y)
])
def hierarchical_intercepts_log_prob(sigma_a, eps_a, gamma_0, gamma_1, b,
sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return hierarchical_intercepts_model(floor, county, log_uranium).log_prob(
[sigma_a, eps_a, gamma_0, gamma_1, b, sigma_y, log_radon])
@tf.function
def sample_hierarchical_intercepts(num_chains, num_results, num_burnin_steps):
"""Samples from the hierarchical intercepts model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=hierarchical_intercepts_log_prob,
num_leapfrog_steps=10,
step_size=0.01)
initial_state = [
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='eps_a'),
tf.zeros([num_chains], name='init_gamma_0'),
tf.zeros([num_chains], name='init_gamma_1'),
tf.zeros([num_chains], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Exp(), # sigma_a
tfb.Identity(), # eps_a
tfb.Identity(), # gamma_0
tfb.Identity(), # gamma_0
tfb.Identity(), # b
# Maps reals to [0, 100].
tfb.Chain([tfb.Shift(shift=50.),
tfb.Scale(scale=50.),
tfb.Tanh()]) # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
HierarchicalInterceptsModel = collections.namedtuple(
'HierarchicalInterceptsModel',
['sigma_a', 'eps_a', 'gamma_0', 'gamma_1', 'b', 'sigma_y'])
samples, acceptance_probs = sample_hierarchical_intercepts(
num_chains=4, num_results=2000, num_burnin_steps=500)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
hierarchical_intercepts_samples = HierarchicalInterceptsModel._make(samples)
Acceptance Probabilities: [0.9615 0.941 0.955 0.95 ]
for var in ['sigma_a', 'gamma_0', 'gamma_1', 'b', 'sigma_y']:
print(
'R-hat for', var, ':',
tfp.mcmc.potential_scale_reduction(
getattr(hierarchical_intercepts_samples, var)).numpy())
R-hat for sigma_a : 1.0469627 R-hat for gamma_0 : 1.0016835 R-hat for gamma_1 : 1.0097923 R-hat for b : 1.0014259 R-hat for sigma_y : 1.0025403
def plot_hierarchical_intercepts():
mean_and_var = lambda x : [reduce_samples(x, fn) for fn in [np.mean, np.var]]
gamma_0_mean, gamma_0_var = mean_and_var(
hierarchical_intercepts_samples.gamma_0)
gamma_1_mean, gamma_1_var = mean_and_var(
hierarchical_intercepts_samples.gamma_1)
eps_a_means, eps_a_vars = mean_and_var(hierarchical_intercepts_samples.eps_a)
mu_a_means = gamma_0_mean + gamma_1_mean * log_uranium
mu_a_vars = gamma_0_var + np.square(log_uranium) * gamma_1_var
a_means = mu_a_means + eps_a_means[county]
a_stds = np.sqrt(mu_a_vars + eps_a_vars[county])
plt.figure()
plt.scatter(log_uranium, a_means, marker='.', c='C0')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,gamma_0_mean + gamma_1_mean * xvals, 'k--')
plt.xlim(-1, 0.8)
for ui, m, se in zip(log_uranium, a_means, a_stds):
plt.plot([ui, ui], [m - se, m + se], 'C1-', alpha=0.1)
plt.xlabel('County-level uranium')
plt.ylabel('Intercept estimate')
plot_hierarchical_intercepts()
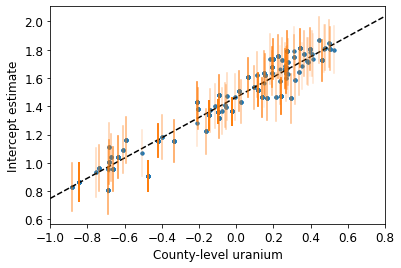
Kesişmelerdeki standart hatalar, ilçe düzeyinde ortak değişkeni olmayan kısmi havuzlama modelinden daha dardır.
6.2 Düzeyler Arası Korelasyonlar
Bazı durumlarda, birden fazla düzeyde yordayıcıya sahip olmak, bireysel düzeydeki değişkenler ve grup artıkları arasındaki korelasyonu ortaya çıkarabilir. Bunu, grup kesişimi modelinde bir ortak değişken olarak bireysel öngörücülerin ortalamasını dahil ederek açıklayabiliriz.
\(\alpha_j = \gamma_0 + \gamma_1 u_j + \gamma_2 \bar{x} + \zeta_j\) Bu geniş bağlamsal etkiler olarak adlandırılır.
mpl.rc("font", size=12)
pgm = daft.PGM([10, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"gamma_prior",
r"$\mathcal{N}(0, 10^5)$",
1.5,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("gamma", r"$\gamma$", 1.5, 3.5))
pgm.add_node(daft.Node("mu_a", r"$\mu_a$", 1.5, 2.2))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
3,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3.5))
pgm.add_node(daft.Node("eps_a", r"$eps_a$", 3, 2.5, scale=1.25))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{Det}$", 1.5, 1.2, scale=1.5))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{U}(0, 100)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2.5))
pgm.add_node(daft.Node("b_prior", r"$\mathcal{N}(0, 10^5)$", 5, 3, fixed=True))
pgm.add_node(daft.Node("b", r"$b$", 5, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("gamma_prior", "gamma")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("sigma_a", "eps_a")
pgm.add_edge("gamma", "mu_a")
pgm.add_edge("mu_a", "a")
pgm.add_edge("eps_a", "a")
pgm.add_edge("b_prior", "b")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([0.9, 2.9, 1.2, 1.0], "$i = 1:3$"))
pgm.add_plate(daft.Plate([2.4, 1.7, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([0.9, 0.4, 1.2, 2.2], "$i = 1:919$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
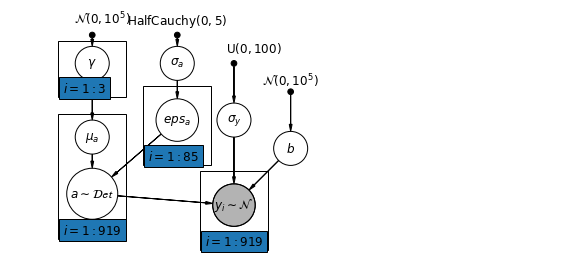
# Create a new variable for mean of floor across counties
xbar = tf.convert_to_tensor(radon.groupby('county')['floor'].mean(), tf.float32)
xbar = tf.gather(xbar, county, axis=-1)
def contextual_effects_model(floor, county, log_uranium, xbar):
"""Creates a joint distribution for the varying slope model."""
return tfd.JointDistributionSequential([
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a: tfd.MultivariateNormalDiag( # eps_a
loc=tf.zeros([num_counties]),
scale_identity_multiplier=sigma_a),
tfd.Normal(loc=0., scale=1e5), # gamma_0
tfd.Normal(loc=0., scale=1e5), # gamma_1
tfd.Normal(loc=0., scale=1e5), # gamma_2
tfd.Normal(loc=0., scale=1e5), # b
tfd.Uniform(low=0., high=100), # sigma_y
lambda sigma_y, b, gamma_2, gamma_1, gamma_0, eps_a: tfd.
MultivariateNormalDiag( # y
loc=affine(
floor, b[..., tf.newaxis],
affine(log_uranium, gamma_1[..., tf.newaxis], gamma_0[
..., tf.newaxis]) + affine(xbar, gamma_2[..., tf.newaxis]) +
tf.gather(eps_a, county, axis=-1)),
scale_identity_multiplier=sigma_y)
])
def contextual_effects_log_prob(sigma_a, eps_a, gamma_0, gamma_1, gamma_2, b,
sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return contextual_effects_model(floor, county, log_uranium, xbar).log_prob(
[sigma_a, eps_a, gamma_0, gamma_1, gamma_2, b, sigma_y, log_radon])
@tf.function
def sample_contextual_effects(num_chains, num_results, num_burnin_steps):
"""Samples from the hierarchical intercepts model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=contextual_effects_log_prob,
num_leapfrog_steps=10,
step_size=0.01)
initial_state = [
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='eps_a'),
tf.zeros([num_chains], name='init_gamma_0'),
tf.zeros([num_chains], name='init_gamma_1'),
tf.zeros([num_chains], name='init_gamma_2'),
tf.zeros([num_chains], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Exp(), # sigma_a
tfb.Identity(), # eps_a
tfb.Identity(), # gamma_0
tfb.Identity(), # gamma_1
tfb.Identity(), # gamma_2
tfb.Identity(), # b
tfb.Chain([tfb.Shift(shift=50.),
tfb.Scale(scale=50.),
tfb.Tanh()]) # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
ContextualEffectsModel = collections.namedtuple(
'ContextualEffectsModel',
['sigma_a', 'eps_a', 'gamma_0', 'gamma_1', 'gamma_2', 'b', 'sigma_y'])
samples, acceptance_probs = sample_contextual_effects(
num_chains=4, num_results=2000, num_burnin_steps=500)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
contextual_effects_samples = ContextualEffectsModel._make(samples)
Acceptance Probabilities: [0.9505 0.9595 0.951 0.9535]
for var in ['sigma_a', 'gamma_0', 'gamma_1', 'gamma_2', 'b', 'sigma_y']:
print(
'R-hat for ', var, ': ',
tfp.mcmc.potential_scale_reduction(
getattr(contextual_effects_samples, var)).numpy())
R-hat for sigma_a : 1.0709597 R-hat for gamma_0 : 1.0067923 R-hat for gamma_1 : 1.0089629 R-hat for gamma_2 : 1.0054177 R-hat for b : 1.0018929 R-hat for sigma_y : 1.0032713
for var in ['gamma_0', 'gamma_1', 'gamma_2']:
var_samples = getattr(contextual_effects_samples, var)
mean = var_samples.numpy().mean()
std = var_samples.numpy().std()
r_hat = tfp.mcmc.potential_scale_reduction(var_samples).numpy()
n_eff = tfp.mcmc.effective_sample_size(var_samples).numpy().sum()
print(var, ' mean: ', mean, ' std: ', std, ' n_eff: ', n_eff, ' r_hat: ',
r_hat)
gamma_0 mean: 1.3934746 std: 0.04966602 n_eff: 816.21265 r_hat: 1.0067923 gamma_1 mean: 0.7229424 std: 0.088611916 n_eff: 1462.486 r_hat: 1.0089629 gamma_2 mean: 0.40893936 std: 0.20304097 n_eff: 457.8165 r_hat: 1.0054177
Bu nedenle, bodrumları olmayan ev oranlarının daha yüksek olduğu ilçelerin temel radon seviyelerinin daha yüksek olma eğiliminde olduğu sonucunu çıkarabiliriz. Belki de bu, ne tür yapıların inşa edildiğini etkileyebilecek olan toprak tipiyle ilgilidir.
6.3 Tahmin
Gelman (2006) havuzlanmamış, havuzlanmış ve kısmen havuzlanmış modellerin tahmin hatasını kontrol etmek için çapraz doğrulama testleri kullanmıştır.
Kök ortalama kare çapraz doğrulama tahmin hataları:
- havuzlanmamış = 0.86
- havuzlanmış = 0.84
- çok düzeyli = 0.79
Çok seviyeli bir modelde yapılabilecek iki tür tahmin vardır:
- Mevcut bir grup içinde yeni bir birey
- Yeni bir grup içinde yeni bir birey
Örneğin, St. Louis ilçesinde bodrumu olmayan yeni bir ev için bir tahmin yapmak istiyorsak, sadece uygun kesişim ile radon modelinden örneklememiz gerekir.
county_name.index('St Louis')
69
Yani,
\[\tilde{y}_i \sim N(\alpha_{69} + \beta (x_i=1), \sigma_y^2)\]
st_louis_log_uranium = tf.convert_to_tensor(
radon.where(radon['county'] == 69)['log_uranium_ppm'].mean(), tf.float32)
st_louis_xbar = tf.convert_to_tensor(
radon.where(radon['county'] == 69)['floor'].mean(), tf.float32)
@tf.function
def intercept_a(gamma_0, gamma_1, gamma_2, eps_a, log_uranium, xbar, county):
return (affine(log_uranium, gamma_1, gamma_0) + affine(xbar, gamma_2) +
tf.gather(eps_a, county, axis=-1))
def contextual_effects_predictive_model(floor, county, log_uranium, xbar,
st_louis_log_uranium, st_louis_xbar):
"""Creates a joint distribution for the contextual effects model."""
return tfd.JointDistributionSequential([
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a: tfd.MultivariateNormalDiag( # eps_a
loc=tf.zeros([num_counties]),
scale_identity_multiplier=sigma_a),
tfd.Normal(loc=0., scale=1e5), # gamma_0
tfd.Normal(loc=0., scale=1e5), # gamma_1
tfd.Normal(loc=0., scale=1e5), # gamma_2
tfd.Normal(loc=0., scale=1e5), # b
tfd.Uniform(low=0., high=100), # sigma_y
# y
lambda sigma_y, b, gamma_2, gamma_1, gamma_0, eps_a: (
tfd.MultivariateNormalDiag(
loc=affine(
floor, b[..., tf.newaxis],
intercept_a(gamma_0[..., tf.newaxis],
gamma_1[..., tf.newaxis], gamma_2[..., tf.newaxis],
eps_a, log_uranium, xbar, county)),
scale_identity_multiplier=sigma_y)),
# stl_pred
lambda _, sigma_y, b, gamma_2, gamma_1, gamma_0, eps_a: tfd.Normal(
loc=intercept_a(gamma_0, gamma_1, gamma_2, eps_a,
st_louis_log_uranium, st_louis_xbar, 69) + b,
scale=sigma_y)
])
@tf.function
def contextual_effects_predictive_log_prob(sigma_a, eps_a, gamma_0, gamma_1,
gamma_2, b, sigma_y, stl_pred):
"""Computes joint log prob pinned at `log_radon`."""
return contextual_effects_predictive_model(floor, county, log_uranium, xbar,
st_louis_log_uranium,
st_louis_xbar).log_prob([
sigma_a, eps_a, gamma_0,
gamma_1, gamma_2, b, sigma_y,
log_radon, stl_pred
])
@tf.function
def sample_contextual_effects_predictive(num_chains, num_results,
num_burnin_steps):
"""Samples from the contextual effects predictive model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=contextual_effects_predictive_log_prob,
num_leapfrog_steps=50,
step_size=0.01)
initial_state = [
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='eps_a'),
tf.zeros([num_chains], name='init_gamma_0'),
tf.zeros([num_chains], name='init_gamma_1'),
tf.zeros([num_chains], name='init_gamma_2'),
tf.zeros([num_chains], name='init_b'),
tf.ones([num_chains], name='init_sigma_y'),
tf.zeros([num_chains], name='init_stl_pred')
]
unconstraining_bijectors = [
tfb.Exp(), # sigma_a
tfb.Identity(), # eps_a
tfb.Identity(), # gamma_0
tfb.Identity(), # gamma_1
tfb.Identity(), # gamma_2
tfb.Identity(), # b
tfb.Chain([tfb.Shift(shift=50.),
tfb.Scale(scale=50.),
tfb.Tanh()]), # sigma_y
tfb.Identity(), # stl_pred
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
ContextualEffectsPredictiveModel = collections.namedtuple(
'ContextualEffectsPredictiveModel', [
'sigma_a', 'eps_a', 'gamma_0', 'gamma_1', 'gamma_2', 'b', 'sigma_y',
'stl_pred'
])
samples, acceptance_probs = sample_contextual_effects_predictive(
num_chains=4, num_results=2000, num_burnin_steps=500)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
contextual_effects_pred_samples = ContextualEffectsPredictiveModel._make(
samples)
Acceptance Probabilities: [0.9165 0.978 0.9755 0.9785]
for var in [
'sigma_a', 'gamma_0', 'gamma_1', 'gamma_2', 'b', 'sigma_y', 'stl_pred'
]:
print(
'R-hat for ', var, ': ',
tfp.mcmc.potential_scale_reduction(
getattr(contextual_effects_pred_samples, var)).numpy())
R-hat for sigma_a : 1.0325582 R-hat for gamma_0 : 1.0033548 R-hat for gamma_1 : 1.0011047 R-hat for gamma_2 : 1.001153 R-hat for b : 1.0020066 R-hat for sigma_y : 1.0128921 R-hat for stl_pred : 1.0058256
plot_traces('stl_pred', contextual_effects_pred_samples.stl_pred, num_chains=4)

plot_posterior('stl_pred', contextual_effects_pred_samples.stl_pred)
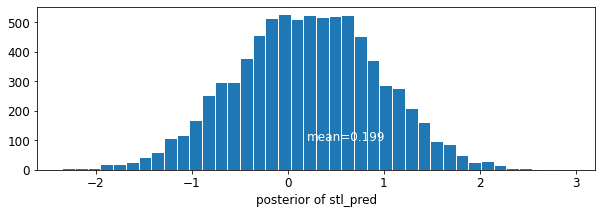
7. Sonuçlar
Çok Düzeyli Modellerin Faydaları:
- Gözlemsel verilerin doğal hiyerarşik yapısının muhasebeleştirilmesi.
- (Az temsil edilen) gruplar için katsayıların tahmini.
- Grup düzeyinde katsayıları tahmin ederken bireysel ve grup düzeyindeki bilgileri dahil etmek.
- Gruplar arasında bireysel düzeyde katsayılar arasında varyasyona izin vermek.
Referanslar
Gelman, A. ve Hill, J. (2006). Regresyon ve Çok Düzeyli/Hiyerarşik Modelleri Kullanarak Veri Analizi (1. baskı). Cambridge Üniversitesi Yayınları.
Gelman, A. (2006). Çok düzeyli (Hiyerarşik) modelleme: ne yapabilir ve ne yapamaz. Teknometri, 48(3), 432–435.
