 הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
כתבתי את המחברת הזו כתיאור מקרה כדי ללמוד את ההסתברות של TensorFlow. הבעיה שבחרתי לפתור היא אומדן מטריצת שיתוף פעולה עבור דגימות של משתנה אקראי גאוסי ממוצע דו-ממדי. לבעיה יש כמה תכונות נחמדות:
- אם אנו משתמשים ב-Wishart הפוך ל-covariance (גישה נפוצה), לבעיה יש פתרון אנליטי, כך שנוכל לבדוק את התוצאות שלנו.
- הבעיה כוללת דגימה של פרמטר מוגבל, מה שמוסיף קצת מורכבות מעניינת.
- הפתרון הפשוט ביותר אינו המהיר ביותר, ולכן יש לבצע עבודת אופטימיזציה מסוימת.
החלטתי לכתוב את החוויות שלי תוך כדי. לקח לי זמן לעטוף את ראשי סביב הנקודות העדינות של TFP, כך שהמחברת הזו מתחילה בצורה פשוטה למדי ואז עובדת בהדרגה עד לתכונות TFP מסובכות יותר. נתקלתי בהרבה בעיות בדרך, וניסיתי ללכוד גם את התהליכים שעזרו לי לזהות אותם וגם את הדרכים לעקיפת הבעיה שמצאתי בסופו של דבר. ניסיתי לכלול הרבה פרטים (כולל המון בדיקות כדי לוודא צעדים בודדים נכונים).
למה ללמוד TensorFlow Probability?
מצאתי את TensorFlow Probability מושכת עבור הפרויקט שלי מכמה סיבות:
- הסתברות TensorFlow מאפשרת לך לפתח אב טיפוס של מודלים מורכבים באופן אינטראקטיבי במחברת. אתה יכול לחלק את הקוד שלך לחתיכות קטנות שתוכל לבדוק באופן אינטראקטיבי ועם בדיקות יחידה.
- ברגע שתהיה מוכן להגדיל, תוכל לנצל את כל התשתית שיש לנו כדי לגרום ל-TensorFlow לפעול על מספר מעבדים מותאמים במספר מכונות.
- לבסוף, למרות שאני מאוד אוהב את סטן, אני מתקשה לבצע ניפוי באגים. אתה צריך לכתוב את כל קוד הדוגמנות שלך בשפה עצמאית שיש בה מעט מאוד כלים לאפשר לך לחטט בקוד שלך, לבדוק מצבי ביניים וכו'.
החיסרון הוא ש- TensorFlow Probability הוא הרבה יותר חדש מ- Stan ו- PyMC3, כך שהתיעוד הוא עבודה בתהליך, ויש הרבה פונקציונליות שעדיין לא נבנתה. לשמחתי, מצאתי שהבסיס של TFP מוצק, והוא מעוצב בצורה מודולרית המאפשרת להרחיב את הפונקציונליות שלו בצורה פשוטה למדי. במחברת זו, בנוסף לפתרון תיאור המקרה, אראה כמה דרכים להרחבת TFP.
למי זה מיועד
אני מניח שהקוראים מגיעים למחברת הזו עם כמה דרישות מוקדמות חשובות. אתה צריך:
- הכר את היסודות של מסקנות בייסיאניות. (אם לא, ספר ראשון ממש נחמד הוא לחשוב מחדש סטטיסטי )
- יש היכרות כלשהי עם ספריית דגימת MCMC, למשל סטן / PyMC3 / באגים
- יש אחיזה מוצקה של numpy (intro טובה אחת היא Python לניתוח נתונים )
- הנה אני בא היכרות חולפת לפחות עם TensorFlow , אך לא בהכרח מומחיות. ( למידה TensorFlow הוא טוב, אבל אמצעי האבולוציה המהירים של TensorFlow שרוב הספרים יהיו מיום קצת. סטנפורד CS20 כמובן הוא גם טוב.)
נסיון ראשון
הנה הניסיון הראשון שלי בבעיה. ספוילר: הפתרון שלי לא עובד, וזה ייקח כמה ניסיונות כדי לתקן את הדברים! למרות שהתהליך אורך זמן מה, כל ניסיון למטה היה שימושי ללימוד חלק חדש של TFP.
הערה אחת: TFP לא מיישם כרגע את התפלגות Wishart ההפוכה (נראה בסוף איך לגלגל את Wishart ההפוכה שלנו), אז במקום זאת אשנה את הבעיה לזו של אומדן מטריצת דיוק באמצעות Wishart קודם.
import collections
import math
import os
import time
import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
שלב 1: אסף את התצפיות
הנתונים שלי כאן הם סינתטיים, אז זה ייראה קצת יותר מסודר מאשר דוגמה בעולם האמיתי. עם זאת, אין סיבה שלא תוכל ליצור כמה נתונים סינתטיים משלך.
טיפ: לאחר שהחלטת על הטופס של המודל שלך, אתה יכול לבחור כמה ערכי פרמטרים ולהשתמש במודל שבחר לייצר כמה נתונים סינטטי. כבדיקת שפיות של היישום שלך, לאחר מכן תוכל לוודא שההערכות שלך כוללות את הערכים האמיתיים של הפרמטרים שבחרת. כדי להפוך את מחזור איתור הבאגים/בדיקה למהיר יותר, כדאי לשקול גרסה פשוטה של המודל שלך (למשל השתמש בפחות ממדים או בפחות דוגמאות).
טיפ: זה הכי קל לעבוד עם התצפיות שלך כמו מערכי numpy. דבר אחד חשוב לציין הוא ש-NumPy כברירת מחדל משתמשת ב-float64, בעוד TensorFlow כברירת מחדל משתמשת ב-float32.
באופן כללי, פעולות TensorFlow רוצות שלכל הארגומנטים יהיה אותו סוג, ואתה צריך לבצע יציקת נתונים מפורשת כדי לשנות סוגים. אם אתה משתמש בתצפיות float64, תצטרך להוסיף הרבה פעולות ליהוק. NumPy, לעומת זאת, תדאג לליהוק באופן אוטומטי. לפיכך, זה הרבה יותר קל להמיר נתוני numpy שלך לתוך float32 מאשר לכפות TensorFlow לשימוש float64.
בחר כמה ערכי פרמטרים
# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)
# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))
[[4. 1.8] [1.8 1. ]] eigenvalues: [4.843075 0.15692513]
צור כמה תצפיות סינתטיות
הערה כי הסתברות TensorFlow משתמשת האמנה כי המימד הראשוני (ים) של הנתונים שלך מייצגים מדדי מדגם, ואת המימד הסופי (ים) של הנתונים מייצגים את הממדיות של דגימות שלך.
כאן אנו רוצים 100 דגימות, שכל אחת מהן היא וקטור באורך 2. אנו ניצור מערך my_data עם הצורה (100, 2). my_data[i, :] הוא \(i\)ה מדגם, וזה וקטור באורך 2.
(זכור להכין my_data יש סוג float32!)
# Set the seed so the results are reproducible.
np.random.seed(123)
# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
mean=true_mean, cov=true_cov, size=100,
check_valid='ignore').astype(np.float32)
my_data.shape
(100, 2)
שפיות תבדוק את התצפיות
מקור פוטנציאלי אחד לבאגים הוא לבלגן את הנתונים הסינתטיים שלך! בוא נעשה כמה בדיקות פשוטות.
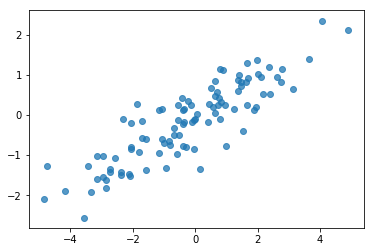
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()
print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)
mean of observations: [-0.24009615 -0.16638893] true mean: [0. 0.]
print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)
covariance of observations: [[3.95307734 1.68718486] [1.68718486 0.94910269]] true covariance: [[4. 1.8] [1.8 1. ]]
אוקיי, הדוגמאות שלנו נראות סבירות. השלב הבא.
שלב 2: הטמע את פונקציית הסיכוי ב-NumPy
הדבר העיקרי שנצטרך לכתוב כדי לבצע את דגימת ה-MCMC שלנו ב-TF Probability הוא פונקציית סבירות יומן. באופן כללי זה קצת יותר מסובך לכתוב TF מאשר NumPy, אז אני מוצא שזה מועיל לבצע יישום ראשוני ב-NumPy. אני הולך לפצל את פונקציית הסבירות לתוך 2 חתיכות, פונקציה סבירה נתונים שמתאימים \(P(data | parameters)\) ו פונקציה סבירה לפני שמתאים \(P(parameters)\).
שים לב שפונקציות NumPy אלה לא חייבות להיות סופר אופטימיזציה / וקטורית מכיוון שהמטרה היא רק ליצור כמה ערכים לבדיקה. נכונות היא השיקול המרכזי!
ראשית ניישם את קטע הסבירות של יומן הנתונים. זה די פשוט. הדבר היחיד שצריך לזכור הוא שאנחנו הולכים לעבוד עם מטריצות מדויקות, אז נבצע פרמטרים בהתאם.
def log_lik_data_numpy(precision, data):
# np.linalg.inv is a really inefficient way to get the covariance matrix, but
# remember we don't care about speed here
cov = np.linalg.inv(precision)
rv = scipy.stats.multivariate_normal(true_mean, cov)
return np.sum(rv.logpdf(data))
# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)
-280.81822950593767
אנחנו הולכים להשתמש Wishart לפני עבור מטריצת הדיוק מאז יש פתרון אנליטי עבור האחוריים (ראה הטבלה השימושית של ויקיפדיה של רשעות קודמות המצומד ).
הפצת Wishart יש 2 פרמטרים:
- מספר דרגות החופש (שכותרתו \(\nu\) בוויקיפדיה)
- מטריצה מידה (שכותרתו \(V\) בוויקיפדיה)
ממוצע לחלוקת Wishart עם פרמטרים \(\nu, V\) הוא \(E[W] = \nu V\), והשונות היא \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)
חלק אינטואיציה שימושי: ניתן ליצור מדגם Wishart ידי יצירת \(\nu\) המבקר הפנה \(x_1 \ldots x_{\nu}\) ממשתנה רב נורמלית אקראית עם 0 ו השונות המשותפת ממוצע \(V\) ולאחר מכן להרכיב את הסכום \(W = \sum_{i=1}^{\nu} x_i x_i^T\).
אם אתה rescale דגימות Wishart ידי חלוקת להם על ידי \(\nu\), אתה מקבל את מטריצת דגימה של \(x_i\). מטריצת מדגם זה אמורה נוטה לכיוון \(V\) כמו \(\nu\) עליות. כאשר \(\nu\) הוא קטן, יש המון וריאציה של מטריצת הדגימה, ולכן ערכים קטנים של \(\nu\) מקביל הרשעות קודמות החלשות וערכים גדולים של \(\nu\) מקביל הרשעות קודמות חזקות. הערה כי \(\nu\) חייב להיות לפחות גדול כמו הממד של המרחב שאתה דגימה כן את או אתה תצבור מטריצות יחידות.
נשתמש \(\nu = 3\) כך שיש לנו לפני חלש, ואנחנו ניקח \(V = \frac{1}{\nu} I\) אשר ימשוך האומדן השונה המשותף שלנו כלפי הזהות (יזכיר כי הממוצע הוא \(\nu V\)).
PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF
def log_lik_prior_numpy(precision):
rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
return rv.logpdf(precision)
# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)
-9.103606346649766
חלוק Wishart היא קודם המצומד להערכת מטריקס הדיוק של נורמלי מרובה משתנה עם ממוצע ידוע \(\mu\).
נניח הפרמטרים Wishart לפני הם \(\nu, V\) וכי יש לנו \(n\) תצפיות של נורמלי, מרובת משתנים שלנו \(x_1, \ldots, x_n\). הפרמטרים האחוריים הם \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).
n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
(v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))
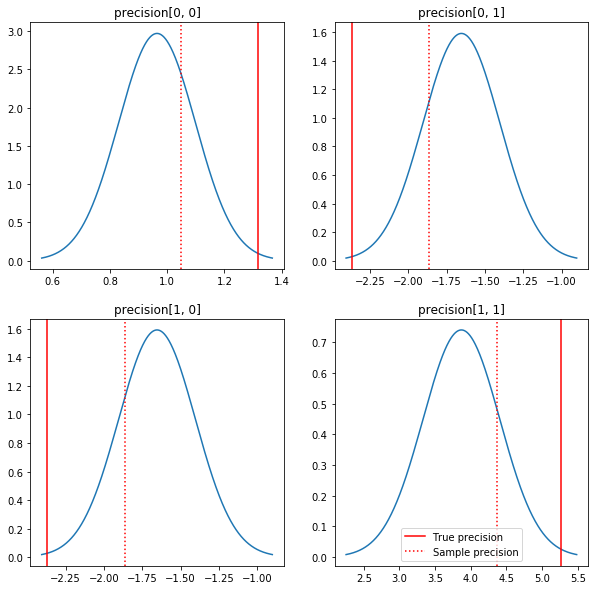
עלילה מהירה של האחוריים והערכים האמיתיים. שימו לב שהחלק האחורי קרוב לחלק האחורי של הדוגמה אך מצטמק מעט לקראת הזהות. שימו לב גם שהערכים האמיתיים די רחוקים מהמצב של האחורי - ככל הנראה זה בגלל שקודם אינו מתאים במיוחד לנתונים שלנו. בשנת בעיה אמיתית היינו עושים סביר טוב עם משהו כמו מדורגים הפוך Wishart מראש את השונות המשותפת (ראו, למשל, של אנדרו גלמן פרשנות בנושא), אבל אז לא היינו בעלי האחורי האנליטי נחמד.
sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
for j in range(2):
ax = axes[i, j]
loc = posterior_mean[i, j]
scale = posterior_sd[i, j]
xmin = loc - 3.0 * scale
xmax = loc + 3.0 * scale
x = np.linspace(xmin, xmax, 1000)
y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
ax.plot(x, y)
ax.axvline(true_precision[i, j], color='red', label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()
שלב 3: הטמע את פונקציית הסבירות ב-TensorFlow
ספוילר: הניסיון הראשון שלנו לא יצליח; נדבר על הסיבה למטה.
טיפ: שימוש TensorFlow להוט מצב בעת פיתוח פונקציות הסבירות שלך. מצב להוט עושה מתנהגים TF יותר כמו numpy - עוסקת בביצוע הכל מיד, כך שתוכל באגים אינטראקטיבי במקום להשתמש Session.run() . עיין בהערות כאן .
מקדים: שיעורי הפצה
ל-TFP יש אוסף של מחלקות הפצה שבהן נשתמש כדי ליצור את ההסתברויות ביומן שלנו. דבר אחד שיש לציין הוא שהמחלקות הללו פועלות עם טנסורים של דגימות ולא רק דגימות בודדות - זה מאפשר וקטוריזציה והאצות קשורות.
התפלגות יכולה לעבוד עם טנסור של דגימות בשתי דרכים שונות. הכי פשוט להמחיש את 2 הדרכים הללו עם דוגמה קונקרטית הכוללת התפלגות עם פרמטר סקלרי יחיד. אני אשתמש פואסון ההפצה, אשר יש rate פרמטר.
- אם אנו יוצרים פואסון עם ערך יחיד עבור
rateפרמטר, קריאה שלהsample()שיטה להחזיר ערך בודד. ערך זה נקראevent, ובמקרה הזה את האירועים כולם scalars. - אם אנו יוצרים פואסון עם מותח של ערכים עבור
rateפרמטר, קריאה שלהsample()שיטה החברה מחזירה ערכים מרובים, אחד לכל ערך מותח שיעור. מטרת מתנהג כאוסף של "חקר עצמאית, כל אחד עם קצב משלו, וכל אחד מן הערכים חזרו ידי קריאהsample()שמתאים לאחד "חקר אלה. אוסף זה של אירועים מופצים עצמאיים אך לא זהה נקראbatch. -
sample()השיטה לוקחתsample_shapeפרמטר אשר מחדל ל tuple ריק. עובר ערך שאינו ריקsample_shapeתוצאות מדגם חוזרות קבוצות מרובות. אוסף של קבוצות זה נקראsample.
א 'של חלוקת log_prob() שיטה צורכת נתונים באופן הקבלות איך sample() מייצר אותו. log_prob() מחזירה הסתברויות עבור דגימות, כלומר עבור מרובים, קבוצות עצמאיות של אירועים.
- אם יש לנו אובייקט פואסון שלנו שנוצרה עם סקלר
rate, כל אצווה הוא סקלר, ואם אנחנו עוברים מותח של דגימות, נצא טנזור באותו גודל של הסתברויות יומן. - אם יש לנו אובייקט פואסון שלנו שנוצרה עם מותח של צורת
Tשלrateערכים, כל אצווה הוא מותח של צורתT. אם נעביר טנזור של דוגמאות של צורה D,T, נוציא טנזור של הסתברויות לוג של צורה D,T.
להלן מספר דוגמאות הממחישות את המקרים הללו. ראה מחברת זו עבור הדרכה מפורטת יותר על אירועים, קבוצות, וצורות.
# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))
# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters. Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))
print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())
iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385] draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]
סבירות יומן נתונים
תחילה ניישם את פונקציית הסבירות של יומן הנתונים.
VALIDATE_ARGS = True
ALLOW_NAN_STATS = False
הבדל מרכזי אחד מהמקרה של NumPy הוא שפונקציית הסבירות TensorFlow שלנו תצטרך לטפל בוקטורים של מטריצות מדויקות ולא רק במטריצות בודדות. וקטורים של פרמטרים ישמשו כאשר נדגום ממספר רשתות.
ניצור אובייקט הפצה שעובד עם אצווה של מטריצות דיוק (כלומר מטריצה אחת לכל שרשרת).
כשמחשבים הסתברויות יומן של הנתונים שלנו, נצטרך לשכפל את הנתונים שלנו באותו אופן כמו הפרמטרים שלנו, כך שיהיה עותק אחד לכל משתנה אצווה. הצורה של הנתונים המשוכפלים שלנו תצטרך להיות כדלקמן:
[sample shape, batch shape, event shape]
במקרה שלנו, צורת האירוע היא 2 (מאחר שאנו עובדים עם גאוסים דו-מימדיים). צורת המדגם היא 100, מכיוון שיש לנו 100 דוגמאות. צורת האצווה תהיה רק מספר המטריצות המדויקות שאנו עובדים איתן. זה בזבוז לשכפל את הנתונים בכל פעם שאנו קוראים לפונקציית הסבירות, ולכן נשכפל את הנתונים מראש ונעבור בגרסה המשוכפלת.
הערה כי מדובר ביישום יעיל: MultivariateNormalFullCovariance הוא יחסית יקרים לכמה חלופות כי נדברנו בפרק אופטימיזציה בסוף.
def log_lik_data(precisions, replicated_data):
n = tf.shape(precisions)[0] # number of precision matrices
# We're estimating a precision matrix; we have to invert to get log
# probabilities. Cholesky inversion should be relatively efficient,
# but as we'll see later, it's even better if we can avoid doing the Cholesky
# decomposition altogether.
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data). We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)
(100, 2, 2)
טיפ: דבר אחד מצאתי להיות מאוד מועיל כותב בדיקות שפיות קטנות של פונקציות TensorFlow שלי. זה ממש קל לבלבל את הווקטוריזציה ב-TF, כך שהפונקציות הפשוטות יותר של NumPy בסביבה היא דרך מצוינת לאמת את פלט TF. תחשוב על אלה כעל בדיקות יחידות קטנות.
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
סבירות יומן קודם
הקודמת קלה יותר מכיוון שאיננו צריכים לדאוג לשכפול נתונים.
@tf.function(autograph=False)
def log_lik_prior(precisions):
rv_precision = tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions)
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]))
print('tensorflow:', lik_tf[i])
0 numpy: -2.2351873809649625 tensorflow: -2.2351875 1 numpy: -9.103606346649766 tensorflow: -9.103608
בנו את פונקציית הסבירות היומן המשותף
פונקציית הסבירות של יומן הנתונים שלמעלה תלויה בתצפיות שלנו, אבל לדוגם לא יהיו כאלה. אנו יכולים להיפטר מהתלות מבלי להשתמש במשתנה גלובלי על ידי שימוש ב-[closure](https://en.wikipedia.org/wiki/Closure_(computer_programming). סגירות כרוכות בפונקציה חיצונית הבונה סביבה המכילה משתנים הדרושים ל- תפקוד פנימי.
def get_log_lik(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik(precision):
return log_lik_data(precision, replicated_data) + log_lik_prior(precision)
return _log_lik
שלב 4: דוגמה
אוקיי, הגיע הזמן לדגום! כדי שהדברים יהיו פשוטים, פשוט נשתמש בשרשרת אחת ונשתמש במטריצת הזהות כנקודת ההתחלה. אנחנו נעשה דברים בזהירות רבה יותר מאוחר יותר.
שוב, זה לא הולך לעבוד - נקבל חריגה.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.expand_dims(tf.eye(2), axis=0)
# Use expand_dims because we want to pass in a tensor of starting values
log_lik_fn = get_log_lik(my_data, n_chains=1)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
return states
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
Cholesky decomposition was not successful. The input might not be valid.
[[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]
Function call stack:
sample
...
Function call stack:
sample
זיהוי הבעיה
InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. זה לא סופר מועיל. בוא נראה אם נוכל לגלות יותר על מה שקרה.
- נדפיס את הפרמטרים עבור כל שלב כדי שנוכל לראות את הערך שעבורו דברים נכשלים
- נוסיף כמה הצהרות כדי להגן מפני בעיות ספציפיות.
קביעות הן מסובכות מכיוון שהן פעולות של TensorFlow, ועלינו לדאוג שהן יבוצעו ולא יעברו אופטימיזציה מהגרף. השווה של זה לקרוא סקירה זו של באגים TensorFlow אם אתה לא מכיר את טענות TF. אתה יכול להכריח טענות מפורשות לבצע באמצעות tf.control_dependencies (ראה דברים בקוד להלן).
הדובר של TensorFlow Print יש פונקציה באותה התנהגות כמו טענות - זה מבצע, ואתה צריך לעשות את זה בהקפדה, כדי להבטיח שהיא מבצעת. Print גורם כאבי ראש נוספים כאשר אנחנו עובדים במחברת: התפוקה שלה נשלחת stderr , ו stderr אינו מוצג בתא. נשתמש טריק כאן: במקום להשתמש tf.Print , ניצור פעולת ההדפסה TensorFlow שלנו באמצעות tf.pyfunc . כמו בקביעות, עלינו לוודא שהשיטה שלנו יוצאת לפועל.
def get_log_lik_verbose(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
def _log_lik(precisions):
# An internal method we'll make into a TensorFlow operation via tf.py_func
def _print_precisions(precisions):
print('precisions:\n', precisions)
return False # operations must return something!
# Turn our method into a TensorFlow operation
print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)
# Assertions are also operations, and some care needs to be taken to ensure
# that they're executed
assert_op = tf.assert_equal(
precisions, tf.linalg.matrix_transpose(precisions),
message='not symmetrical', summarize=4, name='symmetry_check')
# The control_dependencies statement forces its arguments to be executed
# before subsequent operations
with tf.control_dependencies([print_op, assert_op]):
return (log_lik_data(precisions, replicated_data) +
log_lik_prior(precisions))
return _log_lik
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.eye(2)[tf.newaxis, ...]
log_lik_fn = get_log_lik_verbose(my_data)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[ 0.24315196 -0.2761638 ]
[-0.33882257 0.8622 ]]]
assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
[[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]
Function call stack:
sample
...
Function call stack:
sample
למה זה נכשל
ערך הפרמטר החדש הראשון שהדגם מנסה הוא מטריצה א-סימטרית. זה גורם לפירוק Cholesky להיכשל, מכיוון שהוא מוגדר רק עבור מטריצות סימטריות (וחיוביות מוגדרות).
הבעיה כאן היא שפרמטר העניין שלנו הוא מטריצת דיוק, ומטריצות דיוק חייבות להיות אמיתיות, סימטריות וחיוביות מוגדרות. המדגם אינו יודע דבר על האילוץ הזה (למעט אולי דרך מעברים), כך שזה בהחלט אפשרי שהדגם יציע ערך לא חוקי, מה שיוביל לחריגה, במיוחד אם גודל הצעד גדול.
עם הדגימה של המילטון מונטה קרלו, אולי נוכל לעקוף את הבעיה על ידי שימוש בגודל צעד קטן מאוד, מכיוון שהשיפוע אמור להרחיק את הפרמטרים מאזורים לא חוקיים, אבל גדלים קטנים של צעדים פירושם התכנסות איטית. עם סמפלר מטרופוליס-האסטינגס, שלא יודע כלום על שיפועים, נגזר עלינו גורל.
גרסה 2: פרמטרציה מחדש לפרמטרים בלתי מוגבלים
יש פתרון פשוט לבעיה שלמעלה: אנחנו יכולים לשנות את הפרמטרים של המודל שלנו כך שלפרמטרים החדשים לא יהיו יותר אילוצים אלה. TFP מספק קבוצה שימושית של כלים - ביקטורים - לעשות בדיוק את זה.
פרמטריזציה מחדש עם ביקטורים
מטריצת הדיוק שלנו חייבת להיות אמיתית וסימטרית; אנחנו רוצים פרמטריזציה חלופית שאין לה אילוצים אלה. נקודת מוצא היא פירוק Cholesky של מטריצת הדיוק. גורמי Cholesky עדיין מוגבלים - הם משולשים נמוכים יותר, והאלמנטים האלכסוניים שלהם חייבים להיות חיוביים. עם זאת, אם ניקח את הלוג של האלכסונים של גורם Cholesky, היומנים כבר לא מוגבלים להיות חיוביים, ואז אם נשטח את החלק המשולש התחתון לוקטור 1-D, אין לנו יותר את האילוץ המשולש התחתון . התוצאה במקרה שלנו תהיה וקטור אורך 3 ללא אילוצים.
(The ידני סטן יש פרק גדול על שימוש טרנספורמציות כדי להסיר סוגים שונים של אילוצים על פרמטרים.)
לפרמטר מחדש זה יש השפעה מועטה על פונקציית הסבירות של יומן הנתונים שלנו - אנחנו רק צריכים להפוך את הטרנספורמציה שלנו כדי שנחזיר את מטריצת הדיוק - אבל ההשפעה על הקודמת היא יותר מסובכת. ציינו שההסתברות של מטריצת דיוק נתונה נתונה על ידי התפלגות Wishart; מהי ההסתברות למטריצה שעברה טרנספורמציה שלנו?
נזכיר כי, אם ניישם פונקציה מונוטונית \(g\) למשתנה אקראי 1-D \(X\), \(Y = g(X)\), צפיפות עבור \(Y\) ניתנת על ידי
\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]
הנגזרת של \(g^{-1}\) המונח מהווה את הדרך שבה \(g\) משנה כרכים מקומיים. עבור משתנים אקראיים ממדים גבוהים, גורם המתקנת הוא הערך המוחלט של הקובע של יעקוביאן של \(g^{-1}\) (ראה כאן ).
נצטרך להוסיף יעקוביאן של הטרנספורמציה הפוכה לפונקציית הסבירות הקודמת ביומן שלנו. לשמחתי, של הפריון הכולל Bijector בכיתה יכול לטפל זה בשבילנו.
Bijector המעמד משמש כדי לייצג פונקציות להיפוך, חלקה המשמשות לשינוי משתנה ב פונקציית צפיפות. Bijectors ובכולם forward() שיטה שמבצעת לשנות, גידול inverse() שיטה כי ההומוסקסואלים זה, ועל forward_log_det_jacobian() ו inverse_log_det_jacobian() שיטות המספקות את התיקונים יעקוביאן עלינו כשאנחנו reparaterize קובץ PDF.
הפריון הכולל מספק אוסף של bijectors שימושי שנוכל לשלב דרך הרכב באמצעות Chain המפעיל להקים די התמרות מסובך. במקרה שלנו, נרכיב את 3 הביקטורים הבאים (הפעולות בשרשרת מתבצעות מימין לשמאל):
- הצעד הראשון של הטרנספורמציה שלנו הוא ביצוע חלוקה לגורמים של Cholesky על מטריצת הדיוק. אין כיתה ביג'קטור בשביל זה; עם זאת,
CholeskyOuterProductbijector לוקח תוצר של 2 גורמים Cholesky. אנו יכולים להשתמש ההופכי של אותה פעולה באמצעותInvertהמפעיל. - השלב הבא הוא לקחת את היומן של האלמנטים האלכסוניים של גורם Cholesky. אנו משיגים זאת באמצעות
TransformDiagonalbijector ואת ההופכי שלExpbijector. - לבסוף אנו לשטח את החלק המשולש התחתון של המטריצה כדי וקטור באמצעות ההופכי של
FillTriangularbijector.
# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
# step 3: flatten the lower triangular portion of the matrix
tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
# step 2: take the log of the diagonals
tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
# step 1: decompose the precision matrix into its Cholesky factors
tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])
# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)
# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)
print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()
print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())
single input: m: [[1. 2.] [2. 8.]] precision_to_unconstrained(m): [0.6931472 2. 0. ] inverse(precision_to_unconstrained(m)): [[1. 2.] [2. 8.]] tensor of inputs: m2: [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]] precision_to_unconstrained(m2): [[0.6931472 2. 0. ] [0. 0. 0. ]] inverse(precision_to_unconstrained(m2)): [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]]
TransformedDistribution בכיתה לאוטומטי את תהליך החלת bijector להתפלגות ולהפוך את התיקון יעקוביאן צורך log_prob() . הקודקוד החדש שלנו הופך:
def log_lik_prior_transformed(transformed_precisions):
rv_precision = tfd.TransformedDistribution(
tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS),
bijector=precision_to_unconstrained,
validate_args=VALIDATE_ARGS)
return rv_precision.log_prob(transformed_precisions)
# Check against the numpy implementation. Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow: -0.84889317 1 numpy: -7.305657151741624 tensorflow: -7.305659
אנחנו רק צריכים להפוך את הטרנספורמציה עבור סבירות יומן הנתונים שלנו:
precision = precision_to_unconstrained.inverse(transformed_precision)
מכיוון שאנו למעשה רוצים את הפירוק של Cholesky של מטריצת הדיוק, זה יהיה יעיל יותר לעשות כאן רק הפוך חלקי. עם זאת, נשאיר אופטימיזציה למועד מאוחר יותר ונשאיר את ההפוך החלקי כתרגיל עבור הקורא.
def log_lik_data_transformed(transformed_precisions, replicated_data):
# We recover the precision matrix by inverting our bijector. This is
# inefficient since we really want the Cholesky decomposition of the
# precision matrix, and the bijector has that in hand during the inversion,
# but we'll worry about efficiency later.
n = tf.shape(transformed_precisions)[0]
precisions = precision_to_unconstrained.inverse(transformed_precisions)
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
transformed_precisions, replicated_data).numpy()
for i in range(precisions.shape[0]):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
שוב אנו עוטפים את הפונקציות החדשות שלנו בסגירה.
def get_log_lik_transformed(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_transformed(transformed_precisions):
return (log_lik_data_transformed(transformed_precisions, replicated_data) +
log_lik_prior_transformed(transformed_precisions))
return _log_lik_transformed
# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)
[-431.5611]
דְגִימָה
עכשיו, כשאנחנו לא צריכים לדאוג שהדגימה שלנו יתפוצץ בגלל ערכי פרמטר לא חוקיים, בואו ניצור כמה דוגמאות אמיתיות.
הדגימה עובדת עם הגרסה הבלתי מוגבלת של הפרמטרים שלנו, ולכן עלינו לשנות את הערך ההתחלתי שלנו לגרסה הבלתי מוגבלת שלו. הדגימות שאנו יוצרים יהיו גם הן בצורתן הבלתי מוגבלת, אז אנחנו צריכים לשנות אותן בחזרה. ביג'קטורים מוקטורים, כך שקל לעשות זאת.
# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_value = initial_value_cholesky.dot(
initial_value_cholesky.T)[np.newaxis, ...]
# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
initial_value).numpy()
# Sample!
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)
num_results = 1000
num_burnin_steps = 1000
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
initial_value_transformed,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=lambda _, pkr: pkr.is_accepted,
seed=123)
# transform samples back to their constrained form
precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
בואו נשווה את ממוצע הפלט של הדגימה שלנו לממוצע האחורי האנליטי!
print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Sample mean: [[ 1.4315274 -0.25587553] [-0.25587553 0.5740424 ]]
אנחנו רחוקים! בואו נבין למה. ראשית בואו נסתכל על הדוגמאות שלנו.
np.reshape(precision_samples, [-1, 2, 2])
array([[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
...,
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]]], dtype=float32)
אה הו - נראה שלכולם יש אותו ערך. בואו נבין למה.
kernel_results_ משתנה הוא tuple בשם שנותן מידע על סמפלר בכל מדינה. is_accepted השדה הוא המפתח כאן.
# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))
[False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] Fraction of samples accepted: 0.0
כל הדגימות שלנו נדחו! יש להניח שגודל הצעד שלנו היה גדול מדי. בחרתי stepsize=0.1 גרידא שרירותי.
גרסה 3: דגימה עם גודל צעד אדפטיבי
מכיוון שהדגימה עם הבחירה השרירותית שלי של גודל הצעד נכשלה, יש לנו כמה סעיפים בסדר היום:
- ליישם גודל צעד אדפטיבי, ו
- לבצע כמה בדיקות התכנסות.
יש כמה דוגמאות קוד נחמד ב tensorflow_probability/python/mcmc/hmc.py ליישום בגדלי צעד אדפטיבית. התאמתי את זה למטה.
שים לב שיש נפרדות sess.run() הצהרה עבור כל שלב. זה באמת מועיל לניפוי באגים, מכיוון שהוא מאפשר לנו להוסיף בקלות אבחון לפי שלב במידת הצורך. לדוגמה, אנו יכולים להציג התקדמות מצטברת, זמן כל שלב וכו'.
טיפ: דרך נפוצה כנראה אחת לבלגן הדגימה שלך הוא לקבל grow הגרף שלך בלולאה. (הסיבה לסיום הגרף לפני הפעלת ההפעלה היא למנוע בדיוק בעיות כאלה.) אם לא השתמשת ב-finalize(), אבל בדיקת ניפוי שימושית אם הקוד שלך מאט לסריקה היא להדפיס את הגרף גודל בכול שלב באמצעות len(mygraph.get_operations()) - אם העליות האורכות, אתה כנראה עושה משהו רע.
אנחנו הולכים להפעיל כאן 3 רשתות עצמאיות. ביצוע השוואות בין השרשראות יעזור לנו לבדוק התכנסות.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values = []
for i in range(N_CHAINS):
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)
initial_values_transformed = precision_to_unconstrained.forward(
initial_values).numpy()
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=hmc,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values_transformed,
kernel=adapted_kernel,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
parallel_iterations=1)
# transform samples back to their constrained form
precision_samples = precision_to_unconstrained.inverse(states)
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
בדיקה מהירה: שיעור הקבלה שלנו במהלך הדגימה שלנו קרוב ליעד שלנו של 0.651.
print(np.mean(is_accepted))
0.6190666666666667
אפילו טוב יותר, ממוצע המדגם וסטיית התקן שלנו קרובים למה שאנו מצפים מהפתרון האנליטי.
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96426415 -1.6519215 ] [-1.6519215 3.8614824 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13622096 0.25235635] [0.25235635 0.5394968 ]]
בודק התכנסות
באופן כללי לא יהיה לנו פתרון אנליטי שאפשר לבדוק מולו, אז נצטרך לוודא שהדגימה התכנסה. בדיקת תקן אחת היא גלמן-רובין \(\hat{R}\) נתון, המחייב שרשרות דגימה מרובות. \(\hat{R}\) מודד את המידה שבה שונה (מאמצעי) בין הרשתות עולה מה שניתן היה לצפות אם הרשתות חולקו באופן זהה. ערכים של \(\hat{R}\) קרוב 1 משמשים כדי לציין התכנסות משוערת. ראה את המקור לפרטים.
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0038308 1.0005717] [1.0005717 1.0006068]]
ביקורת דוגמניות
אם לא היה לנו פתרון אנליטי, זה היה הזמן לעשות ביקורת מודל אמיתית.
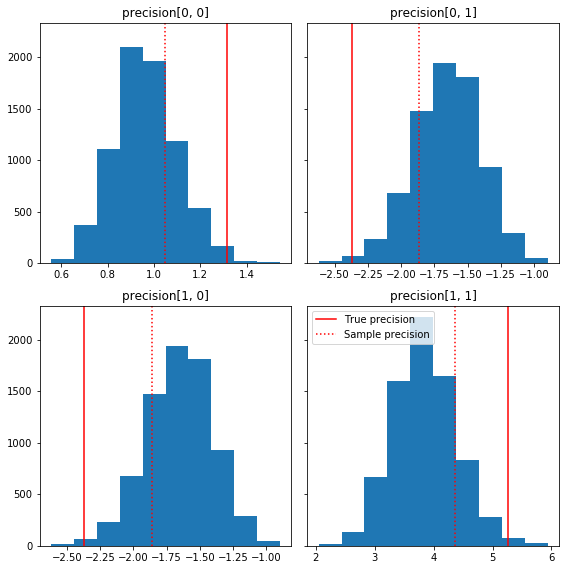
הנה כמה היסטוגרמות מהירות של רכיבי המדגם ביחס לאמת הבסיסית שלנו (באדום). שים לב שהדגימות צומצמו מערכי מטריצת דיוק הדגימה לכיוון מטריצת הזהות הקודמת.
fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
for j in range(2):
ax = axes[i, j]
ax.hist(precision_samples_reshaped[:, i, j])
ax.axvline(true_precision[i, j], color='red',
label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':',
label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()
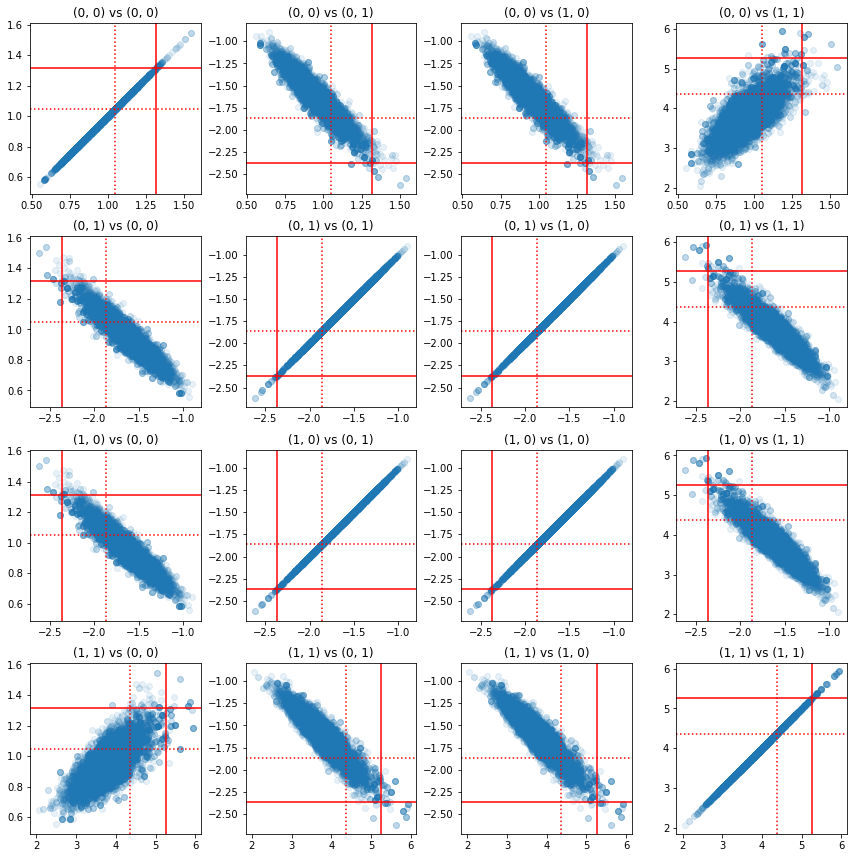
כמה תרשימי פיזור של זוגות של רכיבי דיוק מראים שבגלל מבנה המתאם של החלק האחורי, הערכים האחוריים האמיתיים אינם סבירים כפי שהם מופיעים מהשוליים שלמעלה.
fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
for j1 in range(2):
index1 = 2 * i1 + j1
for i2 in range(2):
for j2 in range(2):
index2 = 2 * i2 + j2
ax = axes[index1, index2]
ax.scatter(precision_samples_reshaped[:, i1, j1],
precision_samples_reshaped[:, i2, j2], alpha=0.1)
ax.axvline(true_precision[i1, j1], color='red')
ax.axhline(true_precision[i2, j2], color='red')
ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()
גרסה 4: דגימה פשוטה יותר של פרמטרים מוגבלים
Bijectors הפכו את הדגימה של מטריצת הדיוק לפשוטה, אבל הייתה כמות לא מבוטלת של המרה ידנית אל וממנו הייצוג הבלתי מוגבל. יש דרך קלה יותר!
The TransformedTransition Kernel
TransformedTransitionKernel מפשט את התהליך הזה. זה עוטף את הדגימה שלך ומטפל בכל ההמרות. זה לוקח כארגומנט רשימה של ביקטורים שממפים ערכי פרמטרים לא מוגבלים לאלו מוגבלים. אז הנה אנחנו צריכים את ההופכי של precision_to_unconstrained bijector השתמשנו לעיל. אנחנו יכולים רק להשתמש tfb.Invert(precision_to_unconstrained) , אבל זה היה כרוך לוקח של inverses של inverses (TensorFlow הוא לא מספיק חכם כדי לפשט tf.Invert(tf.Invert()) כדי tf.Identity()) , אז במקום שאנחנו אני פשוט אכתוב ביקטור חדש.
ביקטור מגביל
# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
# step 3: take the product of Cholesky factors
tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: map a vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()
print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)
m: [[1.0, 2.0], [2.0, 8.0]] unconstrained_to_precision.inverse(m): [0.6931472 2. 0. ] forward(unconstrained_to_precision.inverse(m)): [[1. 2.] [2. 8.]]
דגימה עם TransformedTransitionKernel
עם TransformedTransitionKernel , אנחנו כבר לא צריכים לעשות טרנספורמציות ידנית של הפרמטרים שלנו. הערכים ההתחלתיים שלנו והדגימות שלנו הם כולם מטריצות דיוק; אנחנו רק צריכים להעביר את הביקטור(ים) הלא מגבילים שלנו לגרעין והוא מטפל בכל הטרנספורמציות.
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
return states
precision_samples = sample()
בדיקת התכנסות
\(\hat{R}\) טוב נראה שק התכנסות!
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013582 1.0019467] [1.0019467 1.0011805]]
השוואה מול האחורי האנליטי
שוב בואו נבדוק מול האחורי האנליטי.
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96687526 -1.6552585 ] [-1.6552585 3.867676 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329624 0.24913791] [0.24913791 0.53983927]]
אופטימיזציות
עכשיו, כשיש לנו דברים רצים מקצה לקצה, בואו נעשה גרסה אופטימלית יותר. המהירות לא משנה יותר מדי עבור הדוגמה הזו, אבל ברגע שמטריצות גדלות, כמה אופטימיזציות יעשו הבדל גדול.
שיפור מהירות אחד גדול שאנחנו יכולים לעשות הוא לפרמטר מחדש במונחים של פירוק Cholesky. הסיבה היא שפונקציית סבירות הנתונים שלנו דורשת הן את השונות והן את המטריצות הדיוק. היפוך מטריקס הוא יקר (\(O(n^3)\) עבור \(n \times n\) מטריקס), ואם אנחנו parameterize במונחים של או את השונות המשותפת או המטריצה דיוק, אנחנו צריכים לעשות היפוך לקבל את האחר.
כתזכורת, מטריצה אמיתית, חיובי-מובהק, סימטרי \(M\) ניתן לפרק את המוצר של הטופס \(M = L L^T\) שבו מטריצת \(L\) הוא משולש נמוכה ויש לו אלכסונים חיוביים. בהתחשב פירוק שולסקי של \(M\), נוכל ביעילות יותר להשיג הן \(M\) (תוצר של התחתונה וחדר מטריצה משולשת העליון) ואת \(M^{-1}\) (דרך-החלפה בחזרה). הפירוק של Cholesky עצמו אינו זול לחישוב, אבל אם אנחנו מפרמטרים במונחים של גורמי Cholesky, אנחנו צריכים רק לחשב את Choleksy לגורמים של ערכי הפרמטרים ההתחלתיים.
שימוש בפירוק Cholesky של מטריצת ה-covariance
יש פריון הכולל גרסה של התפלגות הרבה-נורמאלי, MultivariateNormalTriL , כי הוא להם פרמטרים מבחינת גורם Cholesky של המטריצה. אז אם היינו מפרמטרים במונחים של גורם Cholesky של מטריצת השונות, נוכל לחשב את הסבירות ביומן הנתונים ביעילות. האתגר הוא בחישוב סבירות היומן הקודם ביעילות דומה.
אם הייתה לנו גרסה של התפלגות Wishart ההפוכה שעבדה עם גורמי Cholesky של דגימות, היינו מסודרים. אבוי, אנחנו לא. (עם זאת, הצוות יקבל בברכה הגשת קוד!) כחלופה, אנו יכולים להשתמש בגרסה של התפלגות Wishart שעובדת עם גורמי Cholesky של דגימות יחד עם שרשרת של ביקטורים.
נכון לעכשיו חסרים לנו כמה תכשירי מניות כדי להפוך את הדברים ליעילים באמת, אבל אני רוצה להראות את התהליך כתרגיל והמחשה שימושית לכוחם של מכשירי הבייג'קטורים של TFP.
הפצת Wishart הפועלת על גורמי Cholesky
Wishart הפצה יש דגל שימושי, input_output_cholesky , המציין כי מטריצות הקלט והפלט צריך להיות גורמים Cholesky. זה יותר יעיל ומועיל מבחינה מספרית לעבוד עם גורמי Cholesky מאשר מטריצות מלאות, ולכן זה רצוי. נקודה חשובה בנוגע הסמנטיקה של הדגל: זה רק אינדיקציה כי הייצוג של קלט ופלט לחלוקת צריך לשנות - זה אינו מצביע על reparameterization מלא של הפצה, מה שהיה כרוך תיקון יעקוביאן אל log_prob() פוּנקצִיָה. אנחנו בעצם רוצים לעשות את הפרמטר המלא הזה, אז נבנה הפצה משלנו.
# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices. Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).
class CholeskyWishart(tfd.TransformedDistribution):
"""Wishart distribution reparameterized to use Cholesky factors."""
def __init__(self,
df,
scale_tril,
validate_args=False,
allow_nan_stats=True,
name='CholeskyWishart'):
# Wishart has a bunch of methods that we want to support but not
# implement. We'll subclass TransformedDistribution here to take care of
# those. We'll override the few for which speed is critical and implement
# them with a separate Wishart for which input_output_cholesky=True
super(CholeskyWishart, self).__init__(
distribution=tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=False,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
validate_args=validate_args,
name=name
)
# Here's the Cholesky distribution we'll use for log_prob() and sample()
self.cholesky = tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=True,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats)
def _log_prob(self, x):
return (self.cholesky.log_prob(x) +
self.bijector.inverse_log_det_jacobian(x, event_ndims=2))
def _sample_n(self, n, seed=None):
return self.cholesky._sample_n(n, seed)
# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
@tf.function(autograph=False)
def compute_log_prob(m):
w_transformed = tfd.TransformedDistribution(
tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
w_optimized = CholeskyWishart(
df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
log_prob_transformed = w_transformed.log_prob(m)
log_prob_optimized = w_optimized.log_prob(m)
return log_prob_transformed, log_prob_optimized
for matrix in [np.eye(2, dtype=np.float32),
np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
log_prob_transformed, log_prob_optimized = [
t.numpy() for t in compute_log_prob(matrix)]
print('Transformed Wishart:', log_prob_transformed)
print('Optimized Wishart', log_prob_optimized)
Transformed Wishart: -0.84889317 Optimized Wishart -0.84889317 Transformed Wishart: -99.269455 Optimized Wishart -99.269455
בניית התפלגות Wishart הפוכה
יש לנו שלנו השונה המשותפת מטריקס \(C\) מפורקת \(C = L L^T\) שבו \(L\) הוא משולש נמוכה ויש לו אלכסוני חיובי. אנחנו רוצים לדעת את ההסתברות \(L\) בהתחשב בעובדה \(C \sim W^{-1}(\nu, V)\) שבו \(W^{-1}\) הוא ההופכי הפצה Wishart.
חלוקת הפוך Wishart יש את המאפיין שאם \(C \sim W^{-1}(\nu, V)\), אז המטריצה דיוק \(C^{-1} \sim W(\nu, V^{-1})\). אז אנחנו יכולים לקבל את ההסתברות \(L\) באמצעות TransformedDistribution שלוקח כפרמטרים חלוקת Wishart וכן bijector הממפה הגורם Cholesky של מטריקס דיוק כדי גורם Cholesky של ההופכי שלו.
דרך פשוטה (אך לא סופר יעיל) כדי לקבל מהגורם Cholesky של \(C^{-1}\) כדי \(L\) היא להפוך לגורם Cholesky ידי פתרון בחזרה, ואז להרכיב את מטריצת מגורמים הפוכה אלה, ולאחר מכן ביצוע של פרוק Cholesky .
תנו פירוק שולסקי של \(C^{-1} = M M^T\). \(M\) הוא משולש תחתון, כדי שנוכל להפוך אותו באמצעות MatrixInverseTriL bijector.
יצירת \(C\) מ \(M^{-1}\) הוא קצת מסובך: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) הוא משולש נמוך, כך \(M^{-1}\) גם יהיה משולש התחתון, ואת \(M^{-T}\) יהיה משולש עליון. CholeskyOuterProduct() bijector עובד רק עם מטריצות משולשות נמוכות, ולכן אנחנו לא יכולים להשתמש בו כדי ליצור \(C\) מן \(M^{-T}\). הדרך לעקיפת הבעיה שלנו היא שרשרת של ביקטורים שמחלפת את השורות והעמודות של מטריצה.
למרבה המזל ההיגיון הזה הוא כמוס בתוך CholeskyToInvCholesky bijector!
שילוב של כל החלקים
# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()
print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)
numpy = [[ 1.0307764 0. ] [-0.03031695 0.12126781]] bijector = [[ 1.0307764 0. ] [-0.03031695 0.12126781]]
ההפצה הסופית שלנו
Wishart ההפוך שלנו הפועל על גורמי Cholesky הוא כדלקמן:
inverse_wishart_cholesky = tfd.TransformedDistribution(
distribution=CholeskyWishart(
df=PRIOR_DF,
scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
bijector=tfb.CholeskyToInvCholesky())
יש לנו את ווישארט ההפוך, אבל זה די איטי כי אנחנו צריכים לעשות פירוק כולסקי בביקטור. נחזור לפרמטריזציה של המטריצה המדויקת ונראה מה אנחנו יכולים לעשות שם לאופטימיזציה.
גרסה סופית(!): שימוש בפירוק Cholesky של מטריצת הדיוק
גישה חלופית היא לעבוד עם גורמי Cholesky של מטריצת הדיוק. כאן קל לחשב את פונקציית הסבירות הקודמת, אך פונקציית הסבירות של יומן הנתונים דורשת עבודה רבה יותר מכיוון של-TFP אין גרסה של הנורמלי הרב-משתני המוגדרת על ידי דיוק.
אופטימיזציה של סבירות יומן קודם
אנו משתמשים CholeskyWishart ההפצה שבנינו לעיל כדי לבנות את הקודמות.
# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
def log_lik_prior_cholesky(precisions_cholesky):
rv_precision = CholeskyWishart(
df=PRIOR_DF,
scale_tril=PRIOR_SCALE_CHOLESKY,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions_cholesky)
# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
distribution=tfd.WishartTriL(
df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow slow:', lik_tf_slow[i])
print('tensorflow fast:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow slow: -0.84889317 tensorflow fast: -0.84889317 1 numpy: -7.442875031036973 tensorflow slow: -7.442877 tensorflow fast: -7.442876
סבירות אופטימלית של יומן נתונים
We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:
Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)
Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)
Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.
Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now
\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)
So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).
Our approach (courtesy of this notebook ):
- Use
tfd.Independent()to combine a batch of 1-DNormalrandom variables into a single multi-dimensional random variable. Thereinterpreted_batch_ndimsparameter forIndependent()specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, soreinterpreted_batch_ndims=1. - Apply a bijector to add the desired covariance:
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)). Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). Thetfb.Inverttakes care of inverting \(B\), and theadjoint=Trueflag performs the transpose. - Apply a bijector to add the desired offset:
tfb.Shift(shift=shift)Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).
class MVNPrecisionCholesky(tfd.TransformedDistribution):
"""Multivariate normal parameterized by loc and Cholesky precision matrix."""
def __init__(self, loc, precision_cholesky, name=None):
super(MVNPrecisionCholesky, self).__init__(
distribution=tfd.Independent(
tfd.Normal(loc=tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
adjoint=True)),
]),
name=name)
@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
n = tf.shape(precisions_cholesky)[0] # number of precision matrices
rv_data = MVNPrecisionCholesky(
loc=tf.zeros([n, 2]),
precision_cholesky=precisions_cholesky)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.81824
Combined log likelihood function
Now we combine our prior and data log likelihood functions in a closure.
def get_log_lik_cholesky(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_cholesky(precisions_cholesky):
return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
log_lik_prior_cholesky(precisions_cholesky))
return _log_lik_cholesky
Constraining bijector
Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.
unconstrained_to_precision_cholesky = tfb.Chain([
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: expand the vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)
precisions_cholesky: [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]] inv: [[ 0.0000000e+00 0.0000000e+00 0.0000000e+00] [ 3.5762781e-07 -2.0647411e+00 1.3721828e-01]] fwd(inv): [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]]
Initial values
We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values_cholesky = []
for i in range(N_CHAINS):
initial_values_cholesky.append(np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)
Sampling
We sample N_CHAINS chains using the TransformedTransitionKernel .
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_cholesky(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
samples = tf.linalg.matmul(states, states, transpose_b=True)
return samples
precision_samples = sample()
Convergence check
A quick convergence check looks good:
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013583 1.0019467] [1.0019467 1.0011804]]
Comparing results to the analytic posterior
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])
And again, the sample means and standard deviations match those of the analytic posterior.
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.9668749 -1.6552604] [-1.6552604 3.8676758]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329637 0.24913797] [0.24913797 0.53983945]]
Ok, all done! We've got our optimized sampler working.
