Visualizza su TensorFlow.org

Esegui in Google Colab

Visualizza la fonte su GitHub

Scarica taccuino

Ho scritto questo quaderno come caso di studio per imparare la probabilità di TensorFlow. Il problema che ho scelto di risolvere è stimare una matrice di covarianza per campioni di una variabile casuale gaussiana 0 media 2-D. Il problema ha un paio di caratteristiche interessanti:

• Se usiamo un Wishart inverso prima per la covarianza (un approccio comune), il problema ha una soluzione analitica, quindi possiamo controllare i nostri risultati.
• Il problema implica il campionamento di un parametro vincolato, che aggiunge una certa complessità interessante.
• La soluzione più semplice non è quella più veloce, quindi c'è del lavoro di ottimizzazione da fare.

Ho deciso di scrivere le mie esperienze mentre procedevo. Mi ci è voluto un po' per capire i punti più fini della TFP, quindi questo notebook si avvia in modo abbastanza semplice e poi funziona gradualmente fino a funzionalità TFP più complicate. Mi sono imbattuto in molti problemi lungo la strada e ho cercato di catturare sia i processi che mi hanno aiutato a identificarli sia le soluzioni alternative che alla fine ho trovato. Ho cercato di includere un sacco di dettagli (tra cui un sacco di test per assicurarsi passi individuali siano corretti).

Perché imparare la probabilità TensorFlow?

Ho trovato TensorFlow Probability interessante per il mio progetto per alcuni motivi:

• La probabilità TensorFlow ti consente di prototipare lo sviluppo di modelli complessi in modo interattivo in un notebook. Puoi suddividere il tuo codice in piccoli pezzi che puoi testare in modo interattivo e con test unitari.
• Una volta che sei pronto per scalare, puoi sfruttare tutta l'infrastruttura che abbiamo in atto per far funzionare TensorFlow su più processori ottimizzati su più macchine.
• Infine, anche se mi piace molto Stan, trovo piuttosto difficile eseguire il debug. Devi scrivere tutto il tuo codice di modellazione in un linguaggio autonomo che ha pochissimi strumenti per permetterti di frugare nel tuo codice, ispezionare gli stati intermedi e così via.

Il rovescio della medaglia è che TensorFlow Probability è molto più recente di Stan e PyMC3, quindi la documentazione è ancora in corso e ci sono molte funzionalità che devono ancora essere costruite. Fortunatamente, ho trovato le fondamenta di TFP solide ed è progettato in modo modulare che consente di estendere le sue funzionalità in modo abbastanza semplice. In questo quaderno, oltre a risolvere il caso di studio, mostrerò alcuni modi per estendere la TFP.

Per chi è?

Presumo che i lettori arrivino a questo taccuino con alcuni importanti prerequisiti. Dovresti:

• Conoscere le basi dell'inferenza bayesiana. (Se non lo fai, davvero un bel primo libro è Ripensare statistica )
• Avere una certa familiarità con una libreria di campionamento MCMC, ad esempio Stan / PyMC3 / BUGS
• Avere una solida comprensione dei NumPy (Un buon intro è Python per l'analisi dei dati )
• Avere almeno familiarità con passaggio tensorflow , ma non necessariamente esperienza. ( Learning tensorflow è buono, ma rapidi mezzi di evoluzione del tensorflow che maggior parte dei libri sarà un po 'datato. Di Stanford CS20 corso è anche un bene.)

Primo tentativo

Ecco il mio primo tentativo al problema. Spoiler: la mia soluzione non funziona e ci vorranno diversi tentativi per sistemare le cose! Sebbene il processo richieda un po' di tempo, ogni tentativo di seguito è stato utile per apprendere una nuova parte della TFP.

Una nota: TFP attualmente non implementa la distribuzione Wishart inversa (vedremo alla fine come eseguire il roll del nostro Wishart inverso), quindi cambierò il problema con quello di stimare una matrice di precisione utilizzando un Wishart prior.

import collections
import math
import os
import time

import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

Passaggio 1: metti insieme le osservazioni

I miei dati qui sono tutti sintetici, quindi sembrerà un po' più ordinato di un esempio del mondo reale. Tuttavia, non c'è motivo per cui non puoi generare alcuni dati sintetici tuoi.

Suggerimento: Una volta deciso sulla forma del modello, è possibile scegliere alcuni valori di parametro e utilizzare il modello scelto per generare alcuni dati sintetici. Come controllo di integrità della tua implementazione, puoi quindi verificare che le tue stime includano i valori reali dei parametri che hai scelto. Per velocizzare il ciclo di debug/test, potresti prendere in considerazione una versione semplificata del tuo modello (ad es. utilizzare meno dimensioni o meno campioni).

Suggerimento: E 'più facile per il lavoro con le sue osservazioni come array numpy. Una cosa importante da notare è che NumPy per impostazione predefinita utilizza float64, mentre TensorFlow per impostazione predefinita utilizza float32.

In generale, le operazioni di TensorFlow vogliono che tutti gli argomenti abbiano lo stesso tipo e devi eseguire il casting di dati esplicito per cambiare i tipi. Se usi le osservazioni float64, dovrai aggiungere molte operazioni di cast. NumPy, al contrario, si occuperà del casting automaticamente. Quindi, è molto più facile per convertire i dati in NumPy float32 di quello che è per forza tensorflow ad uso float64.

Scegli alcuni valori dei parametri

# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
    np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)

# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))

[[4.  1.8]
 [1.8 1. ]]
eigenvalues:  [4.843075   0.15692513]

Genera alcune osservazioni sintetiche

Si noti che tensorflow Probabilità utilizza la convenzione che la dimensione iniziale (s) completo dei dati rappresentano indici del campione, e la dimensione finale (s) completo dei dati rappresentano la dimensionalità dei vostri campioni.

Qui vogliamo 100 campioni, ognuno dei quali è un vettore di lunghezza 2. ti generano un allineamento my_data di forma (100, 2). my_data[i, :] è il \(i\)esimo campione, ed è un vettore di lunghezza 2.

(Ricordarsi di effettuare my_data avere tipo float32!)

# Set the seed so the results are reproducible.
np.random.seed(123)

# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
    mean=true_mean, cov=true_cov, size=100,
    check_valid='ignore').astype(np.float32)

my_data.shape

(100, 2)

Sanità controlla le osservazioni

Una potenziale fonte di bug sta rovinando i tuoi dati sintetici! Facciamo dei semplici controlli.

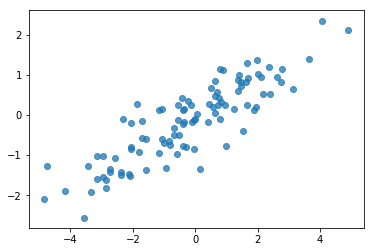
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()

print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)

mean of observations: [-0.24009615 -0.16638893]
true mean: [0. 0.]

print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)

covariance of observations:
 [[3.95307734 1.68718486]
 [1.68718486 0.94910269]]
true covariance:
 [[4.  1.8]
 [1.8 1. ]]

Ok, i nostri campioni sembrano ragionevoli. Passo successivo.

Passaggio 2: implementare la funzione di verosimiglianza in NumPy

La cosa principale che dovremo scrivere per eseguire il nostro campionamento MCMC in TF Probability è una funzione di log verosimiglianza. In generale è un po' più complicato scrivere TF rispetto a NumPy, quindi trovo utile eseguire un'implementazione iniziale in NumPy. Sto per dividere la funzione di verosimiglianza in 2 parti, una funzione di dati probabilità che corrisponde \(P(data | parameters)\) e una funzione di verosimiglianza prima che corrisponde a \(P(parameters)\).

Nota che queste funzioni NumPy non devono essere super ottimizzate / vettorizzate poiché l'obiettivo è solo generare alcuni valori per il test. La correttezza è la considerazione chiave!

Per prima cosa implementeremo il pezzo sulla probabilità del registro dati. È abbastanza semplice. L'unica cosa da ricordare è che lavoreremo con matrici di precisione, quindi parametrizzeremo di conseguenza.

def log_lik_data_numpy(precision, data):
  # np.linalg.inv is a really inefficient way to get the covariance matrix, but
  # remember we don't care about speed here
  cov = np.linalg.inv(precision)
  rv = scipy.stats.multivariate_normal(true_mean, cov)
  return np.sum(rv.logpdf(data))

# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)

-280.81822950593767

Abbiamo intenzione di utilizzare un Wishart preliminare per la matrice di precisione dato che non c'è una soluzione analitica per la parte posteriore (vedere la tabella a portata di mano di Wikipedia dei priori coniugate ).

La distribuzione di Wishart ha 2 parametri:

• il numero di gradi di libertà (etichettato \(\nu\) in Wikipedia)
• una matrice scala (etichettata \(V\) in Wikipedia)

La media per una distribuzione di Wishart con parametri \(\nu, V\) è \(E[W] = \nu V\), e la varianza è \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)

Alcuni intuizione utile: è possibile generare un campione Wishart generando \(\nu\) indipendente disegna \(x_1 \ldots x_{\nu}\) da una variabile casuale normale multivariata con media 0 e covarianza \(V\) e poi formare la somma \(W = \sum_{i=1}^{\nu} x_i x_i^T\).

Se ridimensionare i campioni Wishart da dividendoli per \(\nu\), si ottiene la matrice di covarianza campione del \(x_i\). Questa matrice di covarianza campione dovrebbe tendere \(V\) come \(\nu\) aumenta. Quando \(\nu\) è piccola, c'è un sacco di variazione della matrice di covarianza del campione, così piccoli valori di \(\nu\) corrispondono a priori deboli e grandi valori di \(\nu\) corrispondono a priori forti. Si noti che \(\nu\) devono essere almeno grande come la dimensione dello spazio state campionando o ti generare matrici singolari.

Useremo \(\nu = 3\) quindi abbiamo un debole prima, e noi provvederemo a prendere \(V = \frac{1}{\nu} I\) che tirano la nostra stima di covarianza verso l'identità (ricordiamo che la media è \(\nu V\)).

PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF

def log_lik_prior_numpy(precision):
  rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
  return rv.logpdf(precision)

# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)

-9.103606346649766

La distribuzione Wishart è la prima coniugato per la stima della matrice precisione di un normale multivariata con noti medio \(\mu\).

Supponiamo che i parametri Wishart precedenti sono \(\nu, V\) e che dobbiamo \(n\) osservazioni del nostro multivariata normale, \(x_1, \ldots, x_n\). I parametri posteriori sono \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\).

n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
                       (v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))

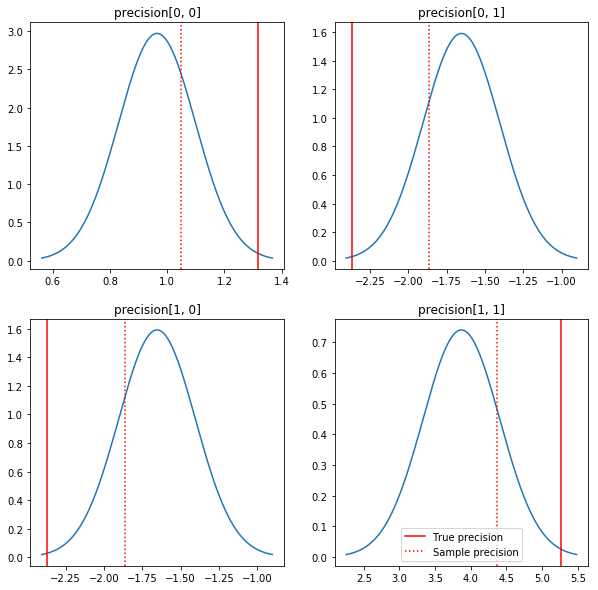
Una rapida trama dei posteriori e dei veri valori. Notare che i posteriori sono vicini ai posteriori del campione ma sono un po' ristretti verso l'identità. Nota anche che i valori veri sono piuttosto lontani dalla modalità del posteriore - presumibilmente questo perché il precedente non è una corrispondenza molto buona per i nostri dati. In un vero e proprio problema avremmo probabilmente meglio con qualcosa di simile a una scala inversa Wishart preliminare per la covarianza (vedi, ad esempio, di Andrew Gelman commento sul tema), ma poi non avremmo un bel posteriore analitica.

sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    loc = posterior_mean[i, j]
    scale = posterior_sd[i, j]
    xmin = loc - 3.0 * scale
    xmax = loc + 3.0 * scale
    x = np.linspace(xmin, xmax, 1000)
    y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
    ax.plot(x, y)
    ax.axvline(true_precision[i, j], color='red', label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()

Passaggio 3: implementare la funzione di verosimiglianza in TensorFlow

Spoiler: il nostro primo tentativo non funzionerà; ne parleremo di seguito.

Suggerimento: l'uso tensorflow modalità ansioso quando si sviluppano le funzioni di probabilità. Modalità Eager rende si comportano più come TF NumPy - tutto esegue immediatamente, in modo da poter eseguire il debug in modo interattivo, invece di dover utilizzare Session.run() . Vedere le note qui .

Preliminari: Classi di distribuzione

TFP ha una raccolta di classi di distribuzione che useremo per generare le nostre probabilità di log. Una cosa da notare è che queste classi funzionano con tensori di campioni anziché solo campioni singoli: ciò consente la vettorizzazione e le relative accelerazioni.

Una distribuzione può funzionare con un tensore di campioni in 2 modi diversi. È più semplice illustrare questi 2 modi con un esempio concreto che coinvolge una distribuzione con un singolo parametro scalare. Userò il Poisson di distribuzione, che ha un rate parametro.

• Se creiamo un Poisson con un unico valore per il rate parametri, una chiamata al suo sample() il metodo restituisce un singolo valore. Questo valore è chiamato un event , e in questo caso gli eventi sono tutti scalari.
• Se creiamo un Poisson con un tensore di valori per la rate dei parametri, una chiamata al suo sample() metodo restituisce ora più valori, uno per ogni valore nel tensore di tasso. L'oggetto agisce come una raccolta di Poissons indipendenti, ciascuna con il proprio tasso, e ciascun valore restituito da una chiamata a sample() corrisponde a uno di questi Poissons. Questa raccolta di eventi identicamente distribuite indipendente ma non è chiamato un batch .
• Il sample() metodo accetta un sample_shape parametro il cui valore predefinito una tupla vuota. Passando un valore non vuoto per sample_shape determina campione corrispondente alla più batch. Questa raccolta di lotti è chiamato un sample .

Di una distribuzione log_prob() metodo consuma i dati in un modo che parallelismi come sample() genera. log_prob() restituisce le probabilità per i campioni, vale a dire per i molteplici, lotti indipendenti di eventi.

• Se abbiamo il nostro oggetto di Poisson che è stato creato con uno scalare rate , ogni lotto è uno scalare, e se si passa in un tensore di campioni, faremo uscire un tensore delle stesse dimensioni delle probabilità di registro.
• Se abbiamo il nostro oggetto di Poisson che è stato creato con un tensore di forma T di rate valori, ogni partita è un tensore di forma T . Se passiamo un tensore di campioni di forma D, T, otterremo un tensore di log probabilità di forma D, T.

Di seguito sono riportati alcuni esempi che illustrano questi casi. Vedere questo notebook per un tutorial più dettagliato su eventi, lotti, e forme.

# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))

# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters.  Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))

print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())

iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385]
draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]

Probabilità del registro dati

Per prima cosa implementeremo la funzione di verosimiglianza del log dei dati.

VALIDATE_ARGS = True
ALLOW_NAN_STATS = False

Una differenza fondamentale rispetto al caso NumPy è che la nostra funzione di verosimiglianza TensorFlow dovrà gestire vettori di matrici di precisione anziché solo singole matrici. I vettori dei parametri verranno utilizzati quando campioniamo da più catene.

Creeremo un oggetto di distribuzione che funziona con un batch di matrici di precisione (cioè una matrice per catena).

Quando calcoliamo le probabilità di log dei nostri dati, avremo bisogno che i nostri dati vengano replicati allo stesso modo dei nostri parametri in modo che ci sia una copia per variabile batch. La forma dei nostri dati replicati dovrà essere la seguente:

[sample shape, batch shape, event shape]

Nel nostro caso, la forma dell'evento è 2 (dato che stiamo lavorando con gaussiane 2-D). La forma del campione è 100, poiché abbiamo 100 campioni. La forma batch sarà solo il numero di matrici di precisione con cui stiamo lavorando. È uno spreco replicare i dati ogni volta che chiamiamo la funzione di verosimiglianza, quindi replicheremo i dati in anticipo e passeremo la versione replicata.

Si noti che questa è un'implementazione inefficiente: MultivariateNormalFullCovariance è costoso rispetto ad alcune alternative che ne parleremo nella sezione Ottimizzazione alla fine.

def log_lik_data(precisions, replicated_data):
  n = tf.shape(precisions)[0]  # number of precision matrices
  # We're estimating a precision matrix; we have to invert to get log
  # probabilities.  Cholesky inversion should be relatively efficient,
  # but as we'll see later, it's even better if we can avoid doing the Cholesky
  # decomposition altogether.
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data).  We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)

(100, 2, 2)

Suggerimento: Una cosa che ho trovato per essere estremamente utile è la scrittura piccoli controlli di integrità delle mie funzioni tensorflow. È davvero facile rovinare la vettorizzazione in TF, quindi avere le funzioni NumPy più semplici in giro è un ottimo modo per verificare l'output di TF. Pensa a questi come piccoli test unitari.

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

log verosimiglianza precedente

Il precedente è più semplice poiché non dobbiamo preoccuparci della replica dei dati.

@tf.function(autograph=False)
def log_lik_prior(precisions):
  rv_precision = tfd.WishartTriL(
      df=PRIOR_DF,
      scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions)

# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]))
  print('tensorflow:', lik_tf[i])

0
numpy: -2.2351873809649625
tensorflow: -2.2351875
1
numpy: -9.103606346649766
tensorflow: -9.103608

Costruisci la funzione di log verosimiglianza congiunta

La funzione di verosimiglianza del registro dati sopra dipende dalle nostre osservazioni, ma il campionatore non le avrà. Possiamo sbarazzarci della dipendenza senza usare una variabile globale usando una [chiusura](https://en.wikipedia.org/wiki/Closure_(computer_programming). Le chiusure coinvolgono una funzione esterna che costruisce un ambiente contenente le variabili necessarie a un funzione interiore.

def get_log_lik(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik(precision):
    return log_lik_data(precision, replicated_data) + log_lik_prior(precision)

  return _log_lik

Passaggio 4: campione

Ok, è ora di assaggiare! Per semplificare le cose, useremo solo 1 catena e useremo la matrice identità come punto di partenza. Faremo le cose con più attenzione in seguito.

Ancora una volta, questo non funzionerà: avremo un'eccezione.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.expand_dims(tf.eye(2), axis=0)

  # Use expand_dims because we want to pass in a tensor of starting values
  log_lik_fn = get_log_lik(my_data, n_chains=1)

  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
     num_results=num_results,
     num_burnin_steps=num_burnin_steps,
     current_state=[
         init_precision,
     ],
     kernel=tfp.mcmc.HamiltonianMonteCarlo(
         target_log_prob_fn=log_lik_fn,
         step_size=0.1,
         num_leapfrog_steps=3),
     trace_fn=None,
     seed=123)
  return states

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

Cholesky decomposition was not successful. The input might not be valid.
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]

Function call stack:
sample
...
Function call stack:
sample

Identificare il problema

InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. Non è molto utile. Vediamo se riusciamo a scoprire di più su quello che è successo.

• Stamperemo i parametri per ogni passaggio in modo da poter vedere il valore per cui le cose falliscono
• Aggiungeremo alcune affermazioni per evitare problemi specifici.

Le asserzioni sono complicate perché sono operazioni TensorFlow e dobbiamo fare attenzione che vengano eseguite e non vengano ottimizzate dal grafico. Vale la pena di leggere questa panoramica di tensorflow debug se non si ha familiarità con le asserzioni TF. È possibile forzare esplicitamente asserzioni da eseguire utilizzando tf.control_dependencies (vedi i commenti nel codice qui sotto).

Natale di tensorflow Print funzione ha lo stesso comportamento di affermazioni - è un'operazione, e avete bisogno di prendere una certa cura per garantire che l'esecuzione. Print provoca mal di testa aggiuntive quando stiamo lavorando su un quaderno: la sua uscita viene inviato a stderr , e stderr non viene visualizzato nella cella. Useremo un trucco: invece di utilizzare tf.Print , creeremo la nostra operazione di stampa tensorflow via tf.pyfunc . Come per le asserzioni, dobbiamo assicurarci che il nostro metodo venga eseguito.

def get_log_lik_verbose(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  def _log_lik(precisions):
    # An internal method we'll make into a TensorFlow operation via tf.py_func
    def _print_precisions(precisions):
      print('precisions:\n', precisions)
      return False  # operations must return something!
    # Turn our method into a TensorFlow operation
    print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)

    # Assertions are also operations, and some care needs to be taken to ensure
    # that they're executed
    assert_op = tf.assert_equal(
        precisions, tf.linalg.matrix_transpose(precisions),
        message='not symmetrical', summarize=4, name='symmetry_check')

    # The control_dependencies statement forces its arguments to be executed
    # before subsequent operations
    with tf.control_dependencies([print_op, assert_op]):
      return (log_lik_data(precisions, replicated_data) +
              log_lik_prior(precisions))

  return _log_lik

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  init_precision = tf.eye(2)[tf.newaxis, ...]
  log_lik_fn = get_log_lik_verbose(my_data)
  # we'll just do a few steps here
  num_results = 10
  num_burnin_steps = 10
  states = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          init_precision,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=None,
      seed=123)

try:
  states = sample()
except Exception as e:
  # shorten the giant stack trace
  lines = str(e).split('\n')
  print('\n'.join(lines[:5]+['...']+lines[-3:]))

precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[1. 0.]
  [0. 1.]]]
precisions:
 [[[ 0.24315196 -0.2761638 ]
  [-0.33882257  0.8622    ]]]
 assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
     [[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]

Function call stack:
sample
...
Function call stack:
sample

Perché questo fallisce?

Il primissimo nuovo valore di parametro che il campionatore prova è una matrice asimmetrica. Ciò fa fallire la decomposizione di Cholesky, poiché è definita solo per matrici simmetriche (e definite positive).

Il problema qui è che il nostro parametro di interesse è una matrice di precisione e le matrici di precisione devono essere reali, simmetriche e definite positive. Il campionatore non sa nulla di questo vincolo (tranne forse attraverso i gradienti), quindi è del tutto possibile che il campionatore proponga un valore non valido, portando a un'eccezione, in particolare se la dimensione del passo è grande.

Con il campionatore hamiltoniano Monte Carlo, potremmo essere in grado di aggirare il problema utilizzando una dimensione del passo molto piccola, poiché il gradiente dovrebbe mantenere i parametri lontani da regioni non valide, ma dimensioni del passo piccole significano una convergenza lenta. Con un campionatore Metropolis-Hastings, che non sa nulla di gradienti, siamo condannati.

Versione 2: riparametrizzazione a parametri non vincolati

C'è una soluzione semplice al problema di cui sopra: possiamo riparametrizzare il nostro modello in modo che i nuovi parametri non abbiano più questi vincoli. TFP fornisce un utile set di strumenti - biiettori - per fare proprio questo.

Riparametrizzazione con biiettori

La nostra matrice di precisione deve essere reale e simmetrica; vogliamo una parametrizzazione alternativa che non abbia questi vincoli. Un punto di partenza è una fattorizzazione di Cholesky della matrice di precisione. I fattori di Cholesky sono ancora vincolati: sono triangolari inferiori e i loro elementi diagonali devono essere positivi. Tuttavia, se prendiamo il log delle diagonali del fattore di Cholesky, i log non sono più vincolati ad essere positivi, e quindi se appiattiamo la porzione triangolare inferiore in un vettore 1-D, non abbiamo più il vincolo triangolare inferiore . Il risultato nel nostro caso sarà un vettore di lunghezza 3 senza vincoli.

(Il manuale di Stan ha un grande capitolo sull'utilizzo di trasformazioni per rimuovere vari tipi di vincoli sui parametri.)

Questa riparametrizzazione ha scarso effetto sulla nostra funzione di verosimiglianza del registro dati - dobbiamo solo invertire la nostra trasformazione in modo da recuperare la matrice di precisione - ma l'effetto sulla precedente è più complicato. Abbiamo specificato che la probabilità di una data matrice di precisione è data dalla distribuzione di Wishart; qual è la probabilità della nostra matrice trasformata?

Ricordiamo che se si applica una funzione monotona \(g\) ad un 1-D variabile casuale \(X\), \(Y = g(X)\), la densità per \(Y\) è dato da

\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]

La derivata di \(g^{-1}\) termine spiega il modo in cui \(g\) cambia volumi locali. Per variabili casuali di dimensione superiore, il fattore di correzione è il valore assoluto del determinante della Jacobiana di \(g^{-1}\) (vedi qui ).

Dovremo aggiungere uno Jacobiano della trasformata inversa nella nostra funzione di verosimiglianza a priori logaritmica. Fortunatamente, di TFP Bijector classe può prendersi cura di questo per noi.

Il Bijector classe viene utilizzata per rappresentare invertibili, funzioni regolari utilizzate per modificare le variabili in funzioni di densità di probabilità. Bijectors tutte un forward() metodo che esegue trasformano, un inverse() metodo che inverte, e forward_log_det_jacobian() e inverse_log_det_jacobian() metodi che forniscono le correzioni Jacobiane dobbiamo quando reparaterize pdf.

PTF fornisce una raccolta di bijectors utili che possiamo unire attraverso composizione tramite la Chain operatore per formare trasformazioni piuttosto complicato. Nel nostro caso andremo a comporre i seguenti 3 biiettori (le operazioni in catena si eseguono da destra a sinistra):

1. Il primo passo della nostra trasformata consiste nell'eseguire una fattorizzazione di Cholesky sulla matrice di precisione. Non esiste una classe Bijector per questo; tuttavia, il CholeskyOuterProduct bijector prende il prodotto di 2 fattori di Cholesky. Possiamo usare l'inverso di tale operazione utilizzando Invert dell'operatore.
2. Il prossimo passo è prendere il log degli elementi diagonali del fattore di Cholesky. Compiamo questo attraverso il TransformDiagonal bijector e l'inverso del Exp bijector.
3. Infine abbiamo appiattire la porzione triangolare inferiore della matrice per un vettore usando l'inverso della FillTriangular bijector.

# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
    # step 3: flatten the lower triangular portion of the matrix
    tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
    # step 2: take the log of the diagonals    
    tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
    # step 1: decompose the precision matrix into its Cholesky factors
    tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])

# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)

# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)

print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()

print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())

single input:
m:
 [[1. 2.]
 [2. 8.]]
precision_to_unconstrained(m):
 [0.6931472 2.        0.       ]
inverse(precision_to_unconstrained(m)):
 [[1. 2.]
 [2. 8.]]

tensor of inputs:
m2:
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]
precision_to_unconstrained(m2):
 [[0.6931472 2.        0.       ]
 [0.        0.        0.       ]]
inverse(precision_to_unconstrained(m2)):
 [[[1. 2.]
  [2. 8.]]

 [[1. 0.]
  [0. 1.]]]

Il TransformedDistribution classe automatizzare il processo di applicazione di una bijector alla distribuzione e rendendo necessaria la correzione Jacobiana per log_prob() . Il nostro nuovo priore diventa:

def log_lik_prior_transformed(transformed_precisions):
  rv_precision = tfd.TransformedDistribution(
      tfd.WishartTriL(
          df=PRIOR_DF,
          scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
          validate_args=VALIDATE_ARGS,
          allow_nan_stats=ALLOW_NAN_STATS),
      bijector=precision_to_unconstrained,
      validate_args=VALIDATE_ARGS)
  return rv_precision.log_prob(transformed_precisions)

# Check against the numpy implementation.  Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
    transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow: -0.84889317
1
numpy: -7.305657151741624
tensorflow: -7.305659

Abbiamo solo bisogno di invertire la trasformazione per la nostra probabilità di log dei dati:

precision = precision_to_unconstrained.inverse(transformed_precision)

Poiché in realtà vogliamo la fattorizzazione di Cholesky della matrice di precisione, sarebbe più efficiente fare solo un'inversa parziale qui. Tuttavia, lasceremo l'ottimizzazione per dopo e lasceremo l'inverso parziale come esercizio per il lettore.

def log_lik_data_transformed(transformed_precisions, replicated_data):
  # We recover the precision matrix by inverting our bijector.  This is
  # inefficient since we really want the Cholesky decomposition of the
  # precision matrix, and the bijector has that in hand during the inversion,
  # but we'll worry about efficiency later.
  n = tf.shape(transformed_precisions)[0]
  precisions = precision_to_unconstrained.inverse(transformed_precisions)
  precisions_cholesky = tf.linalg.cholesky(precisions)
  covariances = tf.linalg.cholesky_solve(
      precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
  rv_data = tfd.MultivariateNormalFullCovariance(
      loc=tf.zeros([n, 2]),
      covariance_matrix=covariances,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)

  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
    transformed_precisions, replicated_data).numpy()

for i in range(precisions.shape[0]):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.8182

Ancora una volta avvolgiamo le nostre nuove funzioni in una chiusura.

def get_log_lik_transformed(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_transformed(transformed_precisions):
    return (log_lik_data_transformed(transformed_precisions, replicated_data) +
            log_lik_prior_transformed(transformed_precisions))

  return _log_lik_transformed

# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)

[-431.5611]

Campionamento

Ora che non dobbiamo preoccuparci che il nostro campionatore esploda a causa di valori di parametro non validi, generiamo alcuni campioni reali.

Il campionatore funziona con la versione non vincolata dei nostri parametri, quindi dobbiamo trasformare il nostro valore iniziale nella sua versione non vincolata. Anche i campioni che generiamo saranno tutti nella loro forma non vincolata, quindi dobbiamo trasformarli di nuovo. I biiettori sono vettorializzati, quindi è facile farlo.

# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
    [[0.5 + np.random.uniform(), 0.0],
     [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
    dtype=np.float32)
initial_value =  initial_value_cholesky.dot(
  initial_value_cholesky.T)[np.newaxis, ...]

# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
  initial_value).numpy()

# Sample!
@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)

  num_results = 1000
  num_burnin_steps = 1000

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_results,
      num_burnin_steps=num_burnin_steps,
      current_state=[
          initial_value_transformed,
      ],
      kernel=tfp.mcmc.HamiltonianMonteCarlo(
          target_log_prob_fn=log_lik_fn,
          step_size=0.1,
          num_leapfrog_steps=3),
      trace_fn=lambda _, pkr: pkr.is_accepted,
      seed=123)
  # transform samples back to their constrained form
  precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

Confrontiamo la media dell'output del nostro campionatore con la media analitica a posteriori!

print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Sample mean:
 [[ 1.4315274  -0.25587553]
 [-0.25587553  0.5740424 ]]

Siamo lontani! Scopriamo perché. Per prima cosa diamo un'occhiata ai nostri campioni.

np.reshape(precision_samples, [-1, 2, 2])

array([[[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       ...,

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]],

       [[ 1.4315385, -0.2558777],
        [-0.2558777,  0.5740494]]], dtype=float32)

Uh oh - sembra che abbiano tutti lo stesso valore. Scopriamo perché.

Il kernel_results_ variabile è una tupla di nome che dà informazioni sul campionatore in ogni stato. Il is_accepted campo è la chiave qui.

# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))

[False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False False False False False False False False False
 False False False False]
Fraction of samples accepted: 0.0

Tutti i nostri campioni sono stati rifiutati! Presumibilmente il nostro passo era troppo grande. Ho scelto stepsize=0.1 puramente arbitrario.

Versione 3: campionamento con passo adattivo

Poiché il campionamento con la mia scelta arbitraria della dimensione del passo non è riuscito, abbiamo alcuni punti all'ordine del giorno:

1. implementare una dimensione del passo adattivo, e
2. eseguire alcuni controlli di convergenza.

C'è alcuni esempi di codice bello in tensorflow_probability/python/mcmc/hmc.py per l'attuazione di misure di passo adattive. L'ho adattato di seguito.

Si noti che c'è un separato sess.run() dichiarazione per ogni passaggio. Questo è davvero utile per il debug, poiché ci consente di aggiungere facilmente alcuni diagnostici per passaggio, se necessario. Ad esempio, possiamo mostrare progressi incrementali, cronometrare ogni passaggio, ecc.

Suggerimento: Un modo apparentemente comune per rovinare il vostro campionamento è di avere il crescere grafico nel ciclo. (Il motivo per finalizzare il grafico prima dell'esecuzione della sessione è prevenire proprio questi problemi.) Se non hai utilizzato finalize(), tuttavia, un utile controllo di debug se il tuo codice rallenta fino alla scansione è quello di stampare il grafico dimensione ad ogni passo con len(mygraph.get_operations()) - se gli aumenti di lunghezza, probabilmente stai facendo qualcosa di male.

Gestiremo 3 catene indipendenti qui. Fare alcuni confronti tra le catene ci aiuterà a verificare la convergenza.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values = []
for i in range(N_CHAINS):
  initial_value_cholesky = np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32)
  initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)

initial_values_transformed = precision_to_unconstrained.forward(
  initial_values).numpy()

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_transformed(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=hmc,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states, is_accepted = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values_transformed,
      kernel=adapted_kernel,
      trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
      parallel_iterations=1)
  # transform samples back to their constrained form
  precision_samples = precision_to_unconstrained.inverse(states)
  return states, precision_samples, is_accepted

states, precision_samples, is_accepted = sample()

Un rapido controllo: il nostro tasso di accettazione durante il nostro campionamento è vicino al nostro obiettivo di 0,651.

print(np.mean(is_accepted))

0.6190666666666667

Ancora meglio, la media e la deviazione standard del nostro campione sono vicine a quanto ci aspettiamo dalla soluzione analitica.

precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96426415 -1.6519215 ]
 [-1.6519215   3.8614824 ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13622096 0.25235635]
 [0.25235635 0.5394968 ]]

Verifica della convergenza

In generale non avremo una soluzione analitica da confrontare, quindi dovremo assicurarci che il campionatore sia convergente. Un controllo standard è il Gelman-Rubin \(\hat{R}\) statistica, che richiede molteplici catene di campionamento. \(\hat{R}\) misure il grado di varianza (dei mezzi) tra le catene eccede quello che ci si aspetterebbe se le catene sono stati distribuiti in modo identico. Valori di \(\hat{R}\) vicino a 1 sono utilizzati per indicare convergenza approssimativa. Vedere la fonte per i dettagli.

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0038308 1.0005717]
 [1.0005717 1.0006068]]

Critica del modello

Se non avessimo una soluzione analitica, questo sarebbe il momento di fare una vera critica al modello.

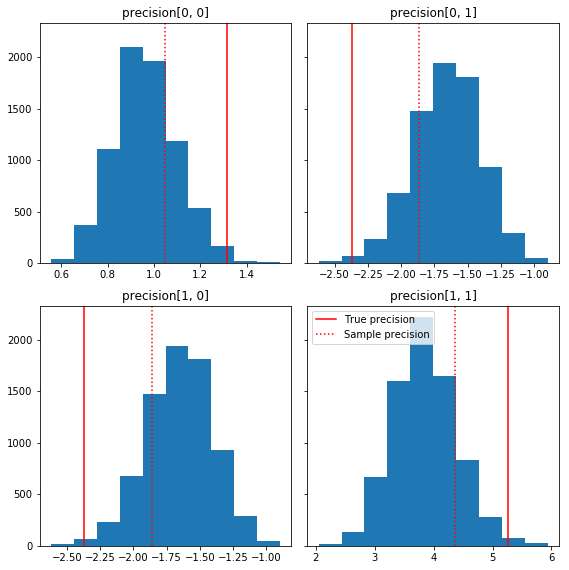
Ecco alcuni rapidi istogrammi dei componenti del campione relativi alla nostra verità di base (in rosso). Si noti che i campioni sono stati ridotti dai valori della matrice di precisione del campione alla matrice identità precedente.

fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
  for j in range(2):
    ax = axes[i, j]
    ax.hist(precision_samples_reshaped[:, i, j])
    ax.axvline(true_precision[i, j], color='red',
               label='True precision')
    ax.axvline(sample_precision[i, j], color='red', linestyle=':',
               label='Sample precision')
    ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()

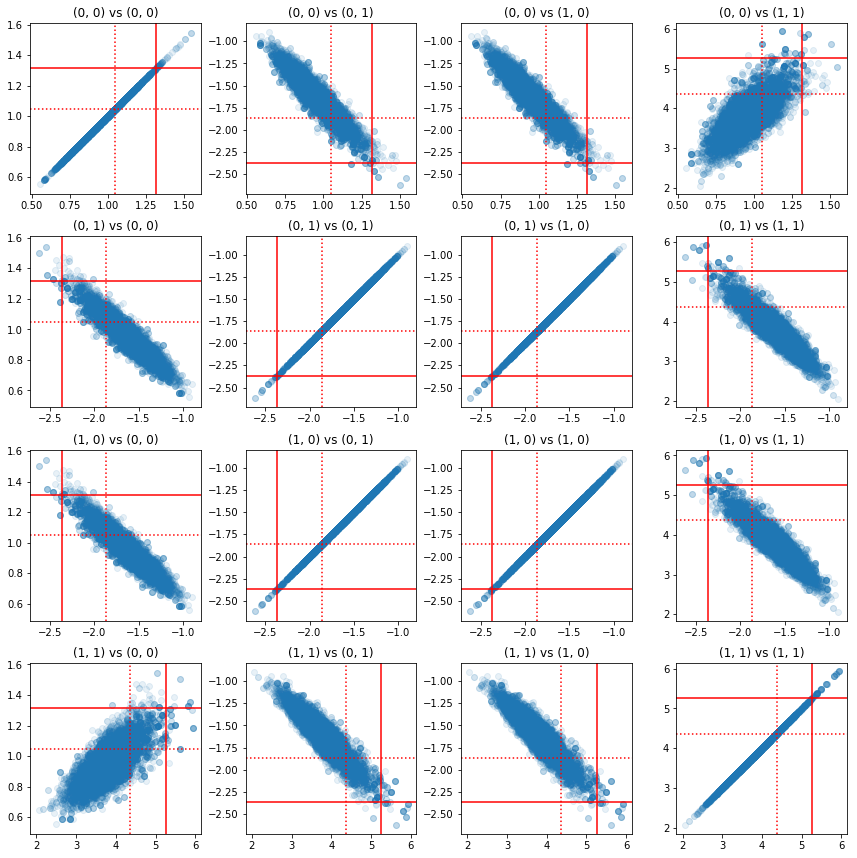
Alcuni grafici a dispersione di coppie di componenti di precisione mostrano che, a causa della struttura di correlazione del posteriore, i veri valori posteriori non sono così improbabili come appaiono dai margini sopra.

fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
  for j1 in range(2):
    index1 = 2 * i1 + j1
    for i2 in range(2):
      for j2 in range(2):
        index2 = 2 * i2 + j2
        ax = axes[index1, index2]
        ax.scatter(precision_samples_reshaped[:, i1, j1],
                   precision_samples_reshaped[:, i2, j2], alpha=0.1)
        ax.axvline(true_precision[i1, j1], color='red')
        ax.axhline(true_precision[i2, j2], color='red')
        ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
        ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
        ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()

Versione 4: campionamento più semplice dei parametri vincolati

I biiettori hanno reso semplice il campionamento della matrice di precisione, ma c'era una discreta quantità di conversione manuale da e verso la rappresentazione non vincolata. C'è un modo più semplice!

Il Kernel di Transizione Trasformato

Il TransformedTransitionKernel semplifica questo processo. Avvolge il tuo campionatore e gestisce tutte le conversioni. Prende come argomento un elenco di biiettori che mappano i valori dei parametri non vincolati a quelli vincolati. Quindi qui abbiamo bisogno l'inverso della precision_to_unconstrained bijector abbiamo usato in precedenza. Si potrebbe utilizzare tfb.Invert(precision_to_unconstrained) , ma che comporterebbe assunzione di inversi di inversi (tensorflow non è abbastanza intelligente per semplificare tf.Invert(tf.Invert()) per tf.Identity()) , così invece abbiamo scriverò solo un nuovo biettore.

Biettore vincolante

# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
    # step 3: take the product of Cholesky factors
    tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: map a vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()

print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)

m:
 [[1.0, 2.0], [2.0, 8.0]]
unconstrained_to_precision.inverse(m):
 [0.6931472 2.        0.       ]
forward(unconstrained_to_precision.inverse(m)):
 [[1. 2.]
 [2. 8.]]

Campionamento con TransformedTransitionKernel

Con il TransformedTransitionKernel , non abbiamo più a che fare trasformazioni manuali dei nostri parametri. I nostri valori iniziali ei nostri campioni sono tutte matrici di precisione; dobbiamo solo passare i nostri biiettori non vincolanti al kernel e si occupa di tutte le trasformazioni.

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  return states

precision_samples  = sample()

Verifica della convergenza

Il \(\hat{R}\) sguardi di controllo convergenza bene!

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013582 1.0019467]
 [1.0019467 1.0011805]]

Confronto con il posteriore analitico

Ancora una volta controlliamo contro il posteriore analitico.

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.96687526 -1.6552585 ]
 [-1.6552585   3.867676  ]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329624 0.24913791]
 [0.24913791 0.53983927]]

ottimizzazioni

Ora che abbiamo le cose in esecuzione end-to-end, facciamo una versione più ottimizzata. La velocità non ha molta importanza per questo esempio, ma una volta che le matrici diventano più grandi, alcune ottimizzazioni faranno una grande differenza.

Un grande miglioramento della velocità che possiamo fare è riparametrizzare in termini di decomposizione di Cholesky. Il motivo è che la nostra funzione di verosimiglianza dei dati richiede sia la covarianza che le matrici di precisione. Inversione di matrice è costoso (\(O(n^3)\) per \(n \times n\) matrice), e se parametrizzare in termini della covarianza o la matrice di precisione, dobbiamo fare un'inversione per ottenere l'altro.

Come promemoria, un vero e proprio, definita positiva, simmetrica matrice \(M\) può essere scomposto in un prodotto di forma \(M = L L^T\) dove la matrice \(L\) è triangolare inferiore e ha diagonali positivi. Data la decomposizione di Cholesky di \(M\), possiamo ottenere più razionalmente, \(M\) (il prodotto di una inferiore e una matrice triangolare superiore) e \(M^{-1}\) (tramite back-sostituzione). La fattorizzazione di Cholesky in sé non è economica da calcolare, ma se parametrizziamo in termini di fattori di Cholesky, dobbiamo solo calcolare la fattorizzazione di Choleksy dei valori dei parametri iniziali.

Usando la decomposizione di Cholesky della matrice di covarianza

TFP ha una versione della distribuzione normale multivariata, MultivariateNormalTriL , che è parametrizzato in termini di fattore di Cholesky della matrice di covarianza. Quindi, se dovessimo parametrizzare in termini di fattore di Cholesky della matrice di covarianza, potremmo calcolare in modo efficiente la verosimiglianza del registro dati. La sfida consiste nel calcolare la probabilità del log precedente con un'efficienza simile.

Se avessimo una versione della distribuzione Wishart inversa che funziona con i fattori di Cholesky dei campioni, saremmo a posto. Ahimè, non lo facciamo. (Il team apprezzerebbe comunque l'invio del codice!) In alternativa, possiamo utilizzare una versione della distribuzione Wishart che funziona con fattori di campioni Cholesky insieme a una catena di biiettori.

Al momento, ci mancano alcuni biiettori di serie per rendere le cose davvero efficienti, ma voglio mostrare il processo come esercizio e un'utile illustrazione della potenza dei biiettori di TFP.

Una distribuzione Wishart che opera su fattori Cholesky

La Wishart distribuzione ha un flag utile, input_output_cholesky , che specifica che le matrici di ingresso e di uscita devono essere fattori di Cholesky. È più efficiente e numericamente vantaggioso lavorare con i fattori di Cholesky rispetto alle matrici complete, motivo per cui è auspicabile. Un punto importante della semantica della bandiera: è solo un'indicazione che la rappresentazione di ingresso e uscita per la distribuzione dovrebbe cambiare - non indica una riparametrizzazione completa della distribuzione, che comporterebbe una correzione Jacobiana al log_prob() funzione. In realtà vogliamo fare questa riparametrizzazione completa, quindi costruiremo la nostra distribuzione.

# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices.  Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).

class CholeskyWishart(tfd.TransformedDistribution):
  """Wishart distribution reparameterized to use Cholesky factors."""
  def __init__(self,
      df,
      scale_tril,
      validate_args=False,
      allow_nan_stats=True,
      name='CholeskyWishart'):
    # Wishart has a bunch of methods that we want to support but not
    # implement.  We'll subclass TransformedDistribution here to take care of
    # those.  We'll override the few for which speed is critical and implement
    # them with a separate Wishart for which input_output_cholesky=True
    super(CholeskyWishart, self).__init__(
        distribution=tfd.WishartTriL(
            df=df,
            scale_tril=scale_tril,
            input_output_cholesky=False,
            validate_args=validate_args,
            allow_nan_stats=allow_nan_stats),
        bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
        validate_args=validate_args,
        name=name
    )
    # Here's the Cholesky distribution we'll use for log_prob() and sample()
    self.cholesky = tfd.WishartTriL(
        df=df,
        scale_tril=scale_tril,
        input_output_cholesky=True,
        validate_args=validate_args,
        allow_nan_stats=allow_nan_stats)

  def _log_prob(self, x):
    return (self.cholesky.log_prob(x) +
            self.bijector.inverse_log_det_jacobian(x, event_ndims=2))

  def _sample_n(self, n, seed=None):
    return self.cholesky._sample_n(n, seed)

# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

@tf.function(autograph=False)
def compute_log_prob(m):
  w_transformed = tfd.TransformedDistribution(
      tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
      bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
  w_optimized = CholeskyWishart(
      df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
  log_prob_transformed = w_transformed.log_prob(m)
  log_prob_optimized = w_optimized.log_prob(m)
  return log_prob_transformed, log_prob_optimized

for matrix in [np.eye(2, dtype=np.float32),
               np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
  log_prob_transformed, log_prob_optimized = [
      t.numpy() for t in compute_log_prob(matrix)]
  print('Transformed Wishart:', log_prob_transformed)
  print('Optimized Wishart', log_prob_optimized)

Transformed Wishart: -0.84889317
Optimized Wishart -0.84889317
Transformed Wishart: -99.269455
Optimized Wishart -99.269455

Costruire una distribuzione Wishart inversa

Abbiamo nostra matrice di covarianza \(C\) decomposto in \(C = L L^T\) dove \(L\) è triangolare inferiore ed ha una diagonale positivo. Vogliamo sapere la probabilità di \(L\) dato che \(C \sim W^{-1}(\nu, V)\) dove \(W^{-1}\) è l'inverso della distribuzione Wishart.

La distribuzione Wishart inversa ha la proprietà che se \(C \sim W^{-1}(\nu, V)\), allora la matrice precisione \(C^{-1} \sim W(\nu, V^{-1})\). Così siamo in grado di ottenere la probabilità di \(L\) tramite un TransformedDistribution che prende come parametri la distribuzione Wishart e un bijector che associa il fattore di Cholesky della matrice di precisione per un fattore di Cholesky della sua inversa.

Un modo semplice (ma non super efficiente) per ottenere dal fattore di Cholesky di \(C^{-1}\) a \(L\) è quello di invertire il fattore di Cholesky da back-solving, poi formando la matrice di covarianza da questi fattori invertiti, e poi facendo una fattorizzazione di Cholesky .

Lasciate che la decomposizione di Cholesky di \(C^{-1} = M M^T\). \(M\) è triangolare inferiore, in modo da poter invertire utilizzando il MatrixInverseTriL bijector.

Formando \(C\) da \(M^{-1}\) è un po 'difficile: \(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\). \(M\) è triangolare inferiore, così \(M^{-1}\) sarà anche triangolare inferiore, e \(M^{-T}\) sarà triangolare superiore. Il CholeskyOuterProduct() bijector funziona solo con matrici triangolari inferiori, quindi non possiamo usare per formare \(C\) da \(M^{-T}\). La nostra soluzione alternativa è una catena di biiettori che permutano le righe e le colonne di una matrice.

Per fortuna questa logica è incapsulata nel CholeskyToInvCholesky bijector!

Combinando tutti i pezzi

# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()

print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)

numpy =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]
bijector =
 [[ 1.0307764   0.        ]
 [-0.03031695  0.12126781]]

La nostra distribuzione finale

Il nostro Wishart inverso che opera sui fattori di Cholesky è il seguente:

inverse_wishart_cholesky = tfd.TransformedDistribution(
    distribution=CholeskyWishart(
        df=PRIOR_DF,
        scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
    bijector=tfb.CholeskyToInvCholesky())

Abbiamo il nostro Wishart inverso, ma è un po' lento perché dobbiamo fare una scomposizione di Cholesky nel biiettore. Torniamo alla parametrizzazione della matrice di precisione e vediamo cosa possiamo fare lì per l'ottimizzazione.

Versione finale(!): usando la decomposizione di Cholesky della matrice di precisione

Un approccio alternativo consiste nel lavorare con i fattori di Cholesky della matrice di precisione. Qui la funzione di verosimiglianza a priori è facile da calcolare, ma la funzione di verosimiglianza del registro dati richiede più lavoro poiché TFP non ha una versione della normale multivariata parametrizzata in base alla precisione.

Probabilità del registro precedente ottimizzata

Usiamo il CholeskyWishart distribuzione abbiamo costruito sopra per costruire la prima.

# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)

def log_lik_prior_cholesky(precisions_cholesky):
  rv_precision = CholeskyWishart(
      df=PRIOR_DF,
      scale_tril=PRIOR_SCALE_CHOLESKY,
      validate_args=VALIDATE_ARGS,
      allow_nan_stats=ALLOW_NAN_STATS)
  return rv_precision.log_prob(precisions_cholesky)

# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
              true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
    distribution=tfd.WishartTriL(
        df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
    bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
    precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
    precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]

for i in range(n):
  print(i)
  print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
  print('tensorflow slow:', lik_tf_slow[i])
  print('tensorflow fast:', lik_tf[i])

0
numpy: -0.8488930160357633
tensorflow slow: -0.84889317
tensorflow fast: -0.84889317
1
numpy: -7.442875031036973
tensorflow slow: -7.442877
tensorflow fast: -7.442876

Probabilità di registrazione dati ottimizzata

We can use TFP's bijectors to build our own version of the multivariate normal. Here is the key idea:

Suppose I have a column vector \(X\) whose elements are iid samples of \(N(0, 1)\). We have \(\text{mean}(X) = 0\) and \(\text{cov}(X) = I\)

Now let \(Y = A X + b\). We have \(\text{mean}(Y) = b\) and \(\text{cov}(Y) = A A^T\)

Hence we can make vectors with mean \(b\) and covariance \(C\) using the affine transform \(Ax+b\) to vectors of iid standard Normal samples provided \(A A^T = C\). The Cholesky decomposition of \(C\) has the desired property. However, there are other solutions.

Let \(P = C^{-1}\) and let the Cholesky decomposition of \(P\) be \(B\), ie \(B B^T = P\). Now

\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)

So another way to get our desired mean and covariance is to use the affine transform \(Y=B^{-T}X + b\).

Our approach (courtesy of this notebook ):

1. Use tfd.Independent() to combine a batch of 1-D Normal random variables into a single multi-dimensional random variable. The reinterpreted_batch_ndims parameter for Independent() specifies the number of batch dimensions that should be reinterpreted as event dimensions. In our case we create a 1-D batch of length 2 that we transform into a 1-D event of length 2, so reinterpreted_batch_ndims=1 .
2. Apply a bijector to add the desired covariance: tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True)) . Note that above we're multiplying our iid normal random variables by the transpose of the inverse of the Cholesky factor of the precision matrix \((B^{-T}X)\). The tfb.Invert takes care of inverting \(B\), and the adjoint=True flag performs the transpose.
3. Apply a bijector to add the desired offset: tfb.Shift(shift=shift) Note that we have to do the shift as a separate step from the initial inverted affine transform because otherwise the inverted scale is applied to the shift (since the inverse of \(y=Ax+b\) is \(x=A^{-1}y - A^{-1}b\)).

class MVNPrecisionCholesky(tfd.TransformedDistribution):
  """Multivariate normal parameterized by loc and Cholesky precision matrix."""

  def __init__(self, loc, precision_cholesky, name=None):
    super(MVNPrecisionCholesky, self).__init__(
        distribution=tfd.Independent(
            tfd.Normal(loc=tf.zeros_like(loc),
                       scale=tf.ones_like(loc)),
            reinterpreted_batch_ndims=1),
        bijector=tfb.Chain([
            tfb.Shift(shift=loc),
            tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
                                  adjoint=True)),
        ]),
        name=name)

@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
  n = tf.shape(precisions_cholesky)[0]  # number of precision matrices
  rv_data = MVNPrecisionCholesky(
      loc=tf.zeros([n, 2]),
      precision_cholesky=precisions_cholesky)
  return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)

# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()

for i in range(n):
  print(i)
  print('numpy:', log_lik_data_numpy(precisions[i], my_data))
  print('tensorflow:', lik_tf[i])

0
numpy: -430.71218815801365
tensorflow: -430.71207
1
numpy: -280.81822950593767
tensorflow: -280.81824

Combined log likelihood function

Now we combine our prior and data log likelihood functions in a closure.

def get_log_lik_cholesky(data, n_chains=1):
  # The data argument that is passed in will be available to the inner function
  # below so it doesn't have to be passed in as a parameter.
  replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])

  @tf.function(autograph=False)
  def _log_lik_cholesky(precisions_cholesky):
    return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
            log_lik_prior_cholesky(precisions_cholesky))

  return _log_lik_cholesky

Constraining bijector

Our samples are constrained to be valid Cholesky factors, which means they must be lower triangular matrices with positive diagonals. The TransformedTransitionKernel needs a bijector that maps unconstrained tensors to/from tensors with our desired constraints. We've removed the Cholesky decomposition from the bijector's inverse, which speeds things up.

unconstrained_to_precision_cholesky = tfb.Chain([
    # step 2: exponentiate the diagonals    
    tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
    # step 1: expand the vector to a lower triangular matrix
    tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])

# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)

precisions_cholesky:
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

inv:
 [[ 0.0000000e+00  0.0000000e+00  0.0000000e+00]
 [ 3.5762781e-07 -2.0647411e+00  1.3721828e-01]]

fwd(inv):
 [[[ 1.         0.       ]
  [ 0.         1.       ]]

 [[ 1.1470785  0.       ]
  [-2.0647411  1.0000004]]]

Initial values

We generate a tensor of initial values. We're working with Cholesky factors, so we generate some Cholesky factor initial values.

# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3

np.random.seed(123)

initial_values_cholesky = []
for i in range(N_CHAINS):
  initial_values_cholesky.append(np.array(
      [[0.5 + np.random.uniform(), 0.0],
       [-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
      dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)

Sampling

We sample N_CHAINS chains using the TransformedTransitionKernel .

@tf.function(autograph=False)
def sample():
  tf.random.set_seed(123)
  log_lik_fn = get_log_lik_cholesky(my_data)

  # Tuning acceptance rates:
  dtype = np.float32
  num_burnin_iter = 3000
  num_warmup_iter = int(0.8 * num_burnin_iter) 
  num_chain_iter = 2500

  # Set the target average acceptance ratio for the HMC as suggested by
  # Beskos et al. (2013):
  # https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
  target_accept_rate = 0.651

  # Initialize the HMC sampler.
  hmc = tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=log_lik_fn,
      step_size=0.01,
      num_leapfrog_steps=3)

  ttk = tfp.mcmc.TransformedTransitionKernel(
      inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)

  # Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
  # of Andrieu and Thoms (2008):
  # http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
  adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
      inner_kernel=ttk,
      num_adaptation_steps=num_warmup_iter,
      target_accept_prob=target_accept_rate)

  states = tfp.mcmc.sample_chain(
      num_results=num_chain_iter,
      num_burnin_steps=num_burnin_iter,
      current_state=initial_values,
      kernel=adapted_kernel,
      trace_fn=None,
      parallel_iterations=1)
  # transform samples back to their constrained form
  samples = tf.linalg.matmul(states, states, transpose_b=True)
  return samples

precision_samples = sample()

Convergence check

A quick convergence check looks good:

r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)

[[1.0013583 1.0019467]
 [1.0019467 1.0011804]]

Comparing results to the analytic posterior

# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])

And again, the sample means and standard deviations match those of the analytic posterior.

print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))

True posterior mean:
 [[ 0.9641779 -1.6534661]
 [-1.6534661  3.8683164]]
Mean of samples:
 [[ 0.9668749 -1.6552604]
 [-1.6552604  3.8676758]]

print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))

True posterior standard deviation:
 [[0.13435492 0.25050813]
 [0.25050813 0.53903675]]
Standard deviation of samples:
 [[0.13329637 0.24913797]
 [0.24913797 0.53983945]]

Ok, all done! We've got our optimized sampler working.