 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запускаем в Google Colab Запускаем в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
Вариационный вывод (VI) бросает приближенный байесовский вывод как проблему оптимизации и ищет «суррогатное» апостериорное распределение, которое минимизирует расхождение KL с истинным апостериорным. Градиентный VI часто работает быстрее, чем методы MCMC, составляет естественным образом с оптимизацией параметров модели и обеспечивает нижнюю границу свидетельства модели, которое можно использовать непосредственно для сравнения моделей, диагностики сходимости и составного вывода.
TensorFlow Probability предлагает инструменты для быстрого, гибкого и масштабируемого VI, которые естественным образом вписываются в стек TFP. Эти инструменты позволяют создавать суррогатные апостериорные модели с ковариационными структурами, индуцированными линейными преобразованиями или нормализующими потоками.
VI может быть использован для оценки Байеса надежных интервалов для параметров регрессионной модели для оценки влияния различных методов лечения или наблюдаемых признаков на исходе интереса. Достоверные интервалы ограничивают значения ненаблюдаемого параметра с определенной вероятностью в соответствии с апостериорным распределением параметра, обусловленным наблюдаемыми данными и с учетом предположения о предшествующем распределении параметра.
В этом Colab мы покажем , как использовать VI для получения достоверных интервалов для параметров байесовского линейных регрессионной модели для уровней радона , измеренных в домах ( с использованием Гельмана коллег (2007) Радон набора данных. , См подобных примеров в Стане). Мы показываем , как TFP JointDistribution s в сочетании с bijectors , чтобы построить и установить два типа выразительных суррогатных апостериорных:
- стандартное нормальное распределение, преобразованное блочной матрицей. Матрица может отражать независимость между некоторыми компонентами апостериорного распределения и зависимость, среди прочего, ослабляя предположение о среднем поле или апостериорной полной ковариации.
- более сложная, более высокая мощность обратного потока авторегрессии .
Суррогатные апостериорные зубы обучаются и сравниваются с результатами суррогатного апостериорного базового значения среднего поля, а также с эталонными выборками из гамильтониана Монте-Карло.
Обзор байесовского вариационного вывода
Предположу , мы имеем следующий порождающий процесс, где \(\theta\) представляет случайные параметры, \(\omega\) представляет детерминированные параметры, и \(x_i\) является особенностью и \(y_i\) являются целевыми значениями для \(i=1,\ldots,n\) наблюдаемых точек данных: \ начать {Выровнять } & \ theta \ sim r (\ Theta) && \ text {(Prior)} \ & \ text {for} i = 1 \ ldots n: \ nonumber \ & \ quad y_i \ sim p (Y_i | x_i, \ theta , \ Omega) && \ текст {(правдоподобие)} \ {конец} выравнивание
Тогда VI характеризуется следующим образом: $ \ newcommand {\ E} {\ operatorname {\ mathbb {E}}} \ newcommand {\ K} {\ operatorname {\ mathbb {K}}} \ newcommand {\ defq} {\ overset {\ tiny \ text {def}} {=}} \ DeclareMathOperator * {\ argmin} {arg \, min} $
\ начинают {Align} - \ лог - р ({y_i} - i ^ п | {x_i} - i ^ п, \ Omega) & \ defeq - \ войти \ Int \ textrm {d} \ тета \, г (\ тета) \ prod_i ^ np (y_i | x_i, \ theta, \ omega) && \ text {(Действительно сложный интеграл)} \ & = - \ log \ int \ textrm {d} \ theta \, q (\ theta) \ frac {1 } {q (\ theta)} r (\ theta) \ prod_i ^ np (y_i | x_i, \ theta, \ omega) && \ text {(Умножить на 1)} \ & \ le - \ int \ textrm {d} \ Theta \ д (\ Theta) \ журнал \ гидроразрыва {г (\ Theta) \ prod_i ^ нп (y_i | х я, \ Theta \ омега)} {Q (\ Theta)} && \ текст {(неравенство Йенсена )} \ & \ defeq \ Е {д (\ Theta)} [- \ лог - р (y_i | x_i, \ Theta, \ омега)] + \ К [д (\ Theta), г (\ Theta)] \ & \ defeq \text{expected negative log likelihood"} + \ текст {Ы регуляризатором"} \ конец {} Align
(Технически мы предполагаем , \(q\) является абсолютно непрерывной относительно \(r\)См. Также, неравенство Йенсена .)
Поскольку оценка верна для всех q, она, очевидно, является наиболее точной для:
\[q^*,w^* = \argmin_{q \in \mathcal{Q},\omega\in\mathbb{R}^d} \left\{ \sum_i^n\E_{q(\Theta)}\left[ -\log p(y_i|x_i,\Theta, \omega) \right] + \K[q(\Theta), r(\Theta)] \right\}\]
Что касается терминологии, мы называем
- \(q^*\) "суррогатной задний," и,
- \(\mathcal{Q}\) "суррогатной семьи."
\(\omega^*\) представляет значения максимального правдоподобия детерминированных параметров на VI потери. Смотрите этот обзор для получения более подробной информации о вариационных умозаключениях.
Пример: байесовская иерархическая линейная регрессия по измерениям Радона.
Радон - это радиоактивный газ, который попадает в дома через точки контакта с землей. Это канцероген, который является основной причиной рака легких у некурящих. Уровни радона сильно различаются от дома к дому.
Агентство по охране окружающей среды провело исследование уровня радона в 80 000 домов. Два важных предиктора:
- Этаж, на котором проводились измерения (радон выше в подвалах)
- Уровень урана в округе (положительная корреляция с уровнями радона)
Предсказание радоновых уровней в домах , сгруппированных по округе классической проблема в байесовском иерархическом моделировании, введенный Гельманом и Хиллами (2006) . Мы построим иерархическую линейную модель для прогнозирования измерений радона в домах, в которой иерархия представляет собой группировку домов по округам. Нас интересуют достоверные интервалы влияния местоположения (округа) на уровень радона в домах в Миннесоте. Чтобы изолировать этот эффект, в модель также включены эффекты пола и уровня урана. Кроме того, мы включим контекстуальный эффект, соответствующий среднему этажу, на котором проводились измерения, по округам, так что если есть различия между округами от этажа, на котором были выполнены измерения, это не связано с эффектом округа.
pip3 install -q tf-nightly tfp-nightly
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
import warnings
tfd = tfp.distributions
tfb = tfp.bijectors
plt.rcParams['figure.facecolor'] = '1.'
# Load the Radon dataset from `tensorflow_datasets` and filter to data from
# Minnesota.
dataset = tfds.as_numpy(
tfds.load('radon', split='train').filter(
lambda x: x['features']['state'] == 'MN').batch(10**9))
# Dependent variable: Radon measurements by house.
dataset = next(iter(dataset))
radon_measurement = dataset['activity'].astype(np.float32)
radon_measurement[radon_measurement <= 0.] = 0.1
log_radon = np.log(radon_measurement)
# Measured uranium concentrations in surrounding soil.
uranium_measurement = dataset['features']['Uppm'].astype(np.float32)
log_uranium = np.log(uranium_measurement)
# County indicator.
county_strings = dataset['features']['county'].astype('U13')
unique_counties, county = np.unique(county_strings, return_inverse=True)
county = county.astype(np.int32)
num_counties = unique_counties.size
# Floor on which the measurement was taken.
floor_of_house = dataset['features']['floor'].astype(np.int32)
# Average floor by county (contextual effect).
county_mean_floor = []
for i in range(num_counties):
county_mean_floor.append(floor_of_house[county == i].mean())
county_mean_floor = np.array(county_mean_floor, dtype=log_radon.dtype)
floor_by_county = county_mean_floor[county]
Модель регрессии определяется следующим образом:
\(\newcommand{\Normal}{\operatorname{\sf Normal} }\)\ начинают {Align} & \ текст {uranium_weight} \ сим \ Нормальный (0, 1) \ & \ текст {county_floor_weight} \ сим \ Нормальный (0, 1) \ & \ текст {для} = 1 \ ldots \ text {num_counties}: \ & \ quad \ text {county_effect} _j \ sim \ Normal (0, \ sigma_c) \ & \ text {for} i = 1 \ ldots n: \ & \ quad \ mu_i = (\ & \ четырехъядерных \ четырехъядерных \ текст {смещения} \ & \ четырехъядерных \ четырехъядерный + \ текст {лен эффект} {\ текст {графство} - i} \ & \ четырехъядерных \ четырехъядерный + \ текст {log_uranium} _i \ Таймс \ текст {uranium_weight } \ & \ четырехъядерных \ четырехъядерный + \ текст {floor_of_house} _i \ Таймс \ текст {floor_weight} \ & \ четырехъядерных \ четырехъядерный + \ текст {floor_by район} {\ текст {графство} _i} \ Таймс \ текст {county_floor_weight}) \ & \ четырехъядерных \ текст {log_radon} _i \ сим \ Normal (\ mu_i \ sigma_y) \ конец {Выравнивание} , в котором \(i\) индексы наблюдения и \(\text{county}_i\) графства , в котором \(i\)го наблюдения было взятый.
Мы используем случайный эффект на уровне округа, чтобы уловить географические различия. Параметры uranium_weight и county_floor_weight моделируются вероятностным, а floor_weight и константа bias являются детерминированными. Эти варианты моделирования в основном произвольны и делаются с целью демонстрации ВИ на вероятностной модели разумной сложности. Для более подробного обсуждения многоуровневого моделирования с фиксированными и случайными эффектами СФПА, используя радон набор данных, см многоуровневого моделирования Primer и фитинг Обобщенных линейной Mixed-эффекты Модели Использования Вариационного Умозаключения .
# Create variables for fixed effects.
floor_weight = tf.Variable(0.)
bias = tf.Variable(0.)
# Variables for scale parameters.
log_radon_scale = tfp.util.TransformedVariable(1., tfb.Exp())
county_effect_scale = tfp.util.TransformedVariable(1., tfb.Exp())
# Define the probabilistic graphical model as a JointDistribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
uranium_weight = yield tfd.Normal(0., scale=1., name='uranium_weight')
county_floor_weight = yield tfd.Normal(
0., scale=1., name='county_floor_weight')
county_effect = yield tfd.Sample(
tfd.Normal(0., scale=county_effect_scale),
sample_shape=[num_counties], name='county_effect')
yield tfd.Normal(
loc=(log_uranium * uranium_weight + floor_of_house* floor_weight
+ floor_by_county * county_floor_weight
+ tf.gather(county_effect, county, axis=-1)
+ bias),
scale=log_radon_scale[..., tf.newaxis],
name='log_radon')
# Pin the observed `log_radon` values to model the un-normalized posterior.
target_model = model.experimental_pin(log_radon=log_radon)
Выразительные суррогатные задницы
Затем мы оцениваем апостериорные распределения случайных эффектов, используя ВИ с двумя разными типами суррогатных апостериоров:
- Многомерное нормальное распределение с ограничениями, ковариационная структура которого вызвана поблочным матричным преобразованием.
- Многофакторное распределение Стандартных Нормальное преобразуется с помощью обратной авторегрессии потока , который затем разделяется и реорганизованным в соответствии с поддержкой задним.
Многомерная нормальная суррогатная задняя часть
Чтобы построить этот суррогатный апостериорный элемент, используется обучаемый линейный оператор, чтобы вызвать корреляцию между компонентами апостериорного.
# Determine the `event_shape` of the posterior, and calculate the size of each
# `event_shape` component. These determine the sizes of the components of the
# underlying standard Normal distribution, and the dimensions of the blocks in
# the blockwise matrix transformation.
event_shape = target_model.event_shape_tensor()
flat_event_shape = tf.nest.flatten(event_shape)
flat_event_size = tf.nest.map_structure(tf.reduce_prod, flat_event_shape)
# The `event_space_bijector` maps unconstrained values (in R^n) to the support
# of the prior -- we'll need this at the end to constrain Multivariate Normal
# samples to the prior's support.
event_space_bijector = target_model.experimental_default_event_space_bijector()
Построить JointDistribution с векторными стандартными нормальными компонентами, с размерами , определяемых соответствующими предыдущими компонентами. Компоненты должны быть векторнозначными, чтобы их можно было преобразовать линейным оператором.
base_standard_dist = tfd.JointDistributionSequential(
[tfd.Sample(tfd.Normal(0., 1.), s) for s in flat_event_size])
Постройте обучаемый поблочный нижнетреугольный линейный оператор. Мы применим его к стандартному нормальному распределению, чтобы реализовать (обучаемое) поблочное матричное преобразование и вызвать корреляционную структуру апостериорного распределения.
В покадрово линейном операторе, A обучаемый полный матричный блок представляет полные ковариации между двумя компонентами задним, в то время как блок нулей (или None ) выражает независимость. Блоки на диагонали являются либо нижнетреугольными, либо диагональными матрицами, так что вся блочная структура представляет собой нижнетреугольную матрицу.
Применение этого биектора к базовому распределению приводит к многомерному нормальному распределению со средним 0 и ковариацией (с учетом фактора Холецкого), равной блочной матрице нижнего треугольника.
operators = (
(tf.linalg.LinearOperatorDiag,), # Variance of uranium weight (scalar).
(tf.linalg.LinearOperatorFullMatrix, # Covariance between uranium and floor-by-county weights.
tf.linalg.LinearOperatorDiag), # Variance of floor-by-county weight (scalar).
(None, # Independence between uranium weight and county effects.
None, # Independence between floor-by-county and county effects.
tf.linalg.LinearOperatorDiag) # Independence among the 85 county effects.
)
block_tril_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
scale_bijector = tfb.ScaleMatvecLinearOperatorBlock(block_tril_linop)
После применения линейного оператора к стандартному нормальному распределению, применяется многослойный Shift , bijector , чтобы среднее принимать ненулевые значения.
loc_bijector = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
Результирующее многомерное Нормальное распределение, полученное путем преобразования стандартного Нормального распределения с помощью бижекторов масштаба и местоположения, должно быть изменено и реструктурировано, чтобы соответствовать предыдущему, и, наконец, ограничено поддержкой предыдущего.
# Reshape each component to match the prior, using a nested structure of
# `Reshape` bijectors wrapped in `JointMap` to form a multipart bijector.
reshape_bijector = tfb.JointMap(
tf.nest.map_structure(tfb.Reshape, flat_event_shape))
# Restructure the flat list of components to match the prior's structure
unflatten_bijector = tfb.Restructure(
tf.nest.pack_sequence_as(
event_shape, range(len(flat_event_shape))))
Теперь соберите все вместе - соедините обучаемые бижекторы вместе и примените их к базовому стандартному нормальному распределению для построения суррогатного апостериорного распределения.
surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
loc_bijector, # allow for nonzero mean
scale_bijector # apply the block matrix transformation to the standard Normal distribution
]))
Обучите многомерную нормальную суррогатную апертуру.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
mvn_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mvn_samples = surrogate_posterior.sample(1000)
mvn_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mvn_samples)
- surrogate_posterior.log_prob(mvn_samples))
print('Multivariate Normal surrogate posterior ELBO: {}'.format(mvn_final_elbo))
plt.plot(mvn_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Multivariate Normal surrogate posterior ELBO: -1065.705322265625
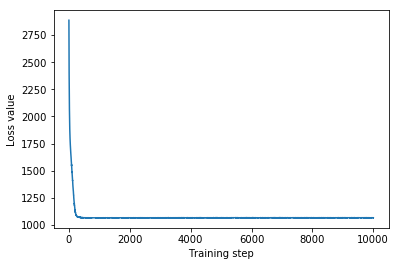
Поскольку обученное суррогатное апостериорное распределение является распределением TFP, мы можем взять из него выборки и обработать их, чтобы получить апостериорные достоверные интервалы для параметров.
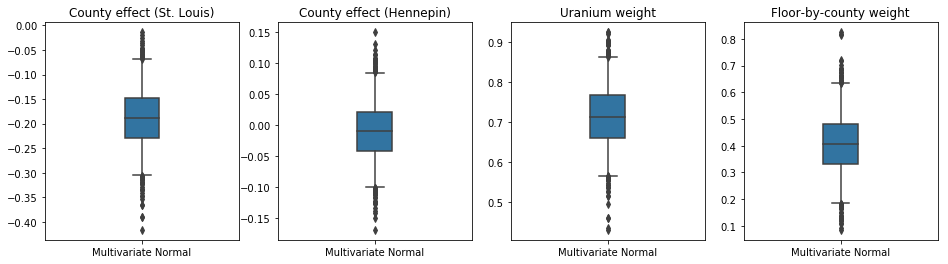
Коробчатые и бачки участки ниже показывают 50% и 95% достоверные интервалы для уездного влияния двух крупнейших графств и весов регрессии по измерениям урана почвы и среднего пола по округе. Апостериорные вероятные интервалы для эффектов округа показывают, что расположение в округе Сент-Луис связано с более низкими уровнями радона после учета других переменных, и что влияние расположения в округе Хеннепин почти нейтрально.
Последующие достоверные интервалы регрессионных весов показывают, что более высокие уровни урана в почве связаны с более высокими уровнями радона, а в округах, где измерения проводились на верхних этажах (вероятно, из-за того, что в доме не было подвала), как правило, наблюдаются более высокие уровни радона. которые могут относиться к свойствам почвы и их влиянию на тип построенных сооружений.
(Детерминированный) коэффициент пола отрицательный, что указывает на то, что нижние этажи имеют более высокие уровни радона, как и ожидалось.
st_louis_co = 69 # Index of St. Louis, the county with the most observations.
hennepin_co = 25 # Index of Hennepin, with the second-most observations.
def pack_samples(samples):
return {'County effect (St. Louis)': samples.county_effect[..., st_louis_co],
'County effect (Hennepin)': samples.county_effect[..., hennepin_co],
'Uranium weight': samples.uranium_weight,
'Floor-by-county weight': samples.county_floor_weight}
def plot_boxplot(posterior_samples):
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
# Invert the results dict for easier plotting.
k = list(posterior_samples.values())[0].keys()
plot_results = {
v: {p: posterior_samples[p][v] for p in posterior_samples} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
sns.boxplot(data=list(var_results.values()), ax=axes[i],
width=0.18*len(var_results), whis=(2.5, 97.5))
# axes[i].boxplot(list(var_results.values()), whis=(2.5, 97.5))
axes[i].title.set_text(var)
fs = 10 if len(var_results) < 4 else 8
axes[i].set_xticklabels(list(var_results.keys()), fontsize=fs)
results = {'Multivariate Normal': pack_samples(mvn_samples)}
print('Bias is: {:.2f}'.format(bias.numpy()))
print('Floor fixed effect is: {:.2f}'.format(floor_weight.numpy()))
plot_boxplot(results)
Bias is: 1.40 Floor fixed effect is: -0.72
Задний суррогат с обратным авторегрессионным потоком
Обратные авторегрессионные потоки (IAF) - это нормализующие потоки, которые используют нейронные сети для захвата сложных нелинейных зависимостей между компонентами распределения. Затем мы строим суррогатную апостериорную модель IAF, чтобы увидеть, превосходит ли эта более гибкая и гибкая модель с ограничениями многомерную нормальную модель.
# Build a standard Normal with a vector `event_shape`, with length equal to the
# total number of degrees of freedom in the posterior.
base_distribution = tfd.Sample(
tfd.Normal(0., 1.), sample_shape=[tf.reduce_sum(flat_event_size)])
# Apply an IAF to the base distribution.
num_iafs = 2
iaf_bijectors = [
tfb.Invert(tfb.MaskedAutoregressiveFlow(
shift_and_log_scale_fn=tfb.AutoregressiveNetwork(
params=2, hidden_units=[256, 256], activation='relu')))
for _ in range(num_iafs)
]
# Split the base distribution's `event_shape` into components that are equal
# in size to the prior's components.
split = tfb.Split(flat_event_size)
# Chain these bijectors and apply them to the standard Normal base distribution
# to build the surrogate posterior. `event_space_bijector`,
# `unflatten_bijector`, and `reshape_bijector` are the same as in the
# multivariate Normal surrogate posterior.
iaf_surrogate_posterior = tfd.TransformedDistribution(
base_distribution,
bijector=tfb.Chain([
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the prior
reshape_bijector, # reshape the vector-valued components to match the shapes of the prior components
split] + # Split the samples into components of the same size as the prior components
iaf_bijectors # Apply a flow model to the Tensor-valued standard Normal distribution
))
Тренируйте суррогатную заднюю часть IAF.
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
iaf_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
iaf_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=4,
jit_compile=True)
iaf_samples = iaf_surrogate_posterior.sample(1000)
iaf_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*iaf_samples)
- iaf_surrogate_posterior.log_prob(iaf_samples))
print('IAF surrogate posterior ELBO: {}'.format(iaf_final_elbo))
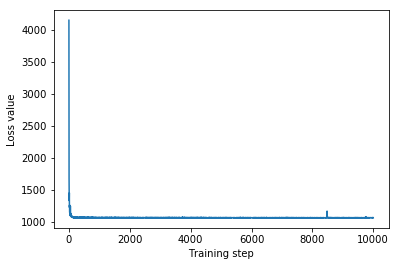
plt.plot(iaf_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
IAF surrogate posterior ELBO: -1065.3663330078125
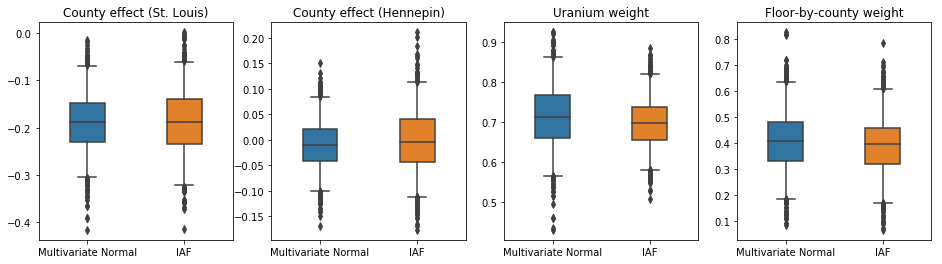
Достоверные интервалы для суррогатного апостериорного интервала IAF кажутся аналогичными интервалам многомерного ограниченного Нормального.
results['IAF'] = pack_samples(iaf_samples)
plot_boxplot(results)
Исходный уровень: суррогатная задняя часть среднего поля
Суррогатные апостериорные распределения VI часто считаются среднеполевыми (независимыми) нормальными распределениями с обучаемыми средними и дисперсиями, которые ограничены поддержкой априорных значений с помощью биективного преобразования. Мы определяем апостериорный суррогат среднего поля в дополнение к двум более выразительным суррогатным апостериорным результатам, используя ту же общую формулу, что и многомерный нормальный суррогатный апостериор.
# A block-diagonal linear operator, in which each block is a diagonal operator,
# transforms the standard Normal base distribution to produce a mean-field
# surrogate posterior.
operators = (tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag)
block_diag_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
mean_field_scale = tfb.ScaleMatvecLinearOperatorBlock(block_diag_linop)
mean_field_loc = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
mean_field_surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
mean_field_loc, # allow for nonzero mean
mean_field_scale # apply the block matrix transformation to the standard Normal distribution
]))
optimizer=tf.optimizers.Adam(learning_rate=1e-2)
mean_field_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
mean_field_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mean_field_samples = mean_field_surrogate_posterior.sample(1000)
mean_field_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mean_field_samples)
- mean_field_surrogate_posterior.log_prob(mean_field_samples))
print('Mean-field surrogate posterior ELBO: {}'.format(mean_field_final_elbo))
plt.plot(mean_field_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Mean-field surrogate posterior ELBO: -1065.7652587890625
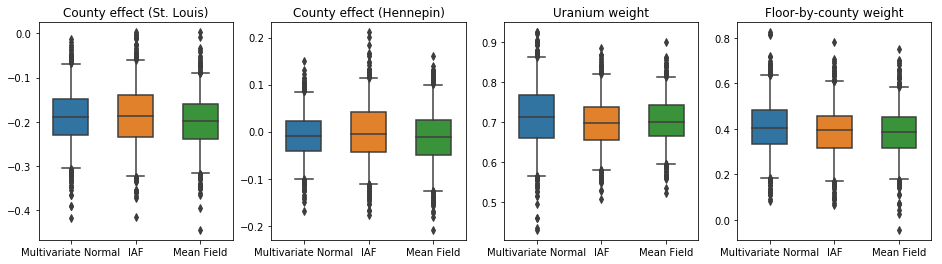
В этом случае апостериорный суррогат среднего поля дает те же результаты, что и более выразительные суррогатные апостериорные данные, указывая на то, что эта более простая модель может быть адекватной для задачи вывода.
results['Mean Field'] = pack_samples(mean_field_samples)
plot_boxplot(results)
Основная правда: гамильтониан Монте-Карло (HMC)
Мы используем HMC для генерации выборок «истинной достоверности» из истинных апостериорных данных для сравнения с результатами суррогатных апостериорных данных.
num_chains = 8
num_leapfrog_steps = 3
step_size = 0.4
num_steps=20000
flat_event_shape = tf.nest.flatten(target_model.event_shape)
enum_components = list(range(len(flat_event_shape)))
bijector = tfb.Restructure(
enum_components,
tf.nest.pack_sequence_as(target_model.event_shape, enum_components))(
target_model.experimental_default_event_space_bijector())
current_state = bijector(
tf.nest.map_structure(
lambda e: tf.zeros([num_chains] + list(e), dtype=tf.float32),
target_model.event_shape))
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_model.unnormalized_log_prob,
num_leapfrog_steps=num_leapfrog_steps,
step_size=[tf.fill(s.shape, step_size) for s in current_state])
hmc = tfp.mcmc.TransformedTransitionKernel(
hmc, bijector)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(num_steps // 2 * 0.8),
target_accept_prob=0.9)
chain, is_accepted = tf.function(
lambda current_state: tfp.mcmc.sample_chain(
current_state=current_state,
kernel=hmc,
num_results=num_steps // 2,
num_burnin_steps=num_steps // 2,
trace_fn=lambda _, pkr:
(pkr.inner_results.inner_results.is_accepted),
),
autograph=False,
jit_compile=True)(current_state)
accept_rate = tf.reduce_mean(tf.cast(is_accepted, tf.float32))
ess = tf.nest.map_structure(
lambda c: tfp.mcmc.effective_sample_size(
c,
cross_chain_dims=1,
filter_beyond_positive_pairs=True),
chain)
r_hat = tf.nest.map_structure(tfp.mcmc.potential_scale_reduction, chain)
hmc_samples = pack_samples(
tf.nest.pack_sequence_as(target_model.event_shape, chain))
print('Acceptance rate is {}'.format(accept_rate))
Acceptance rate is 0.9008625149726868
Постройте образцы трассировок для проверки работоспособности результатов HMC.
def plot_traces(var_name, samples):
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
s = samples.numpy()[:, chain]
axes[0].plot(s, alpha=0.7)
sns.kdeplot(s, ax=axes[1], shade=False)
axes[0].title.set_text("'{}' trace".format(var_name))
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
warnings.filterwarnings('ignore')
for var, var_samples in hmc_samples.items():
plot_traces(var, var_samples)




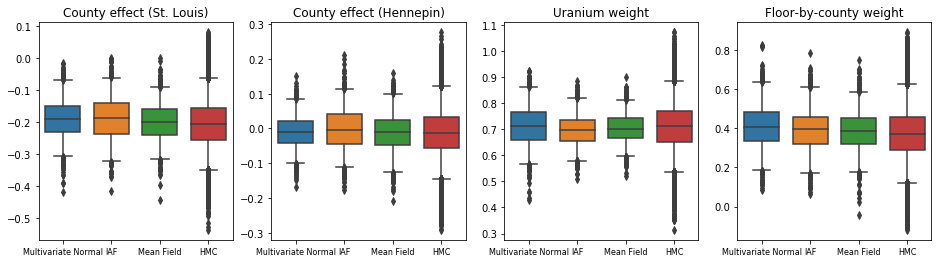
Все три суррогатных апостериора дали достоверные интервалы, которые визуально похожи на образцы HMC, хотя иногда и недостаточно рассредоточены из-за эффекта потери ELBO, как это часто бывает в VI.
results['HMC'] = hmc_samples
plot_boxplot(results)
Дополнительные результаты
Графические функции
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'medium'})
def plot_loss_and_elbo():
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].scatter([0, 1, 2],
[mvn_final_elbo.numpy(),
iaf_final_elbo.numpy(),
mean_field_final_elbo.numpy()])
axes[0].set_xticks(ticks=[0, 1, 2])
axes[0].set_xticklabels(labels=[
'Multivariate Normal', 'IAF', 'Mean Field'])
axes[0].title.set_text('Evidence Lower Bound (ELBO)')
axes[1].plot(mvn_loss, label='Multivariate Normal')
axes[1].plot(iaf_loss, label='IAF')
axes[1].plot(mean_field_loss, label='Mean Field')
axes[1].set_ylim([1000, 4000])
axes[1].set_xlabel('Training step')
axes[1].set_ylabel('Loss (negative ELBO)')
axes[1].title.set_text('Loss')
plt.legend()
plt.show()
plt.rcParams.update({'axes.titlesize': 'medium', 'xtick.labelsize': 'small'})
def plot_kdes(num_chains=8):
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
k = list(results.values())[0].keys()
plot_results = {
v: {p: results[p][v] for p in results} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
ax = axes[i % 2, i // 2]
for posterior, posterior_results in var_results.items():
if posterior == 'HMC':
label = posterior
for chain in range(num_chains):
sns.kdeplot(
posterior_results[:, chain],
ax=ax, shade=False, color='k', linestyle=':', label=label)
label=None
else:
sns.kdeplot(
posterior_results, ax=ax, shade=False, label=posterior)
ax.title.set_text('{}'.format(var))
ax.legend()
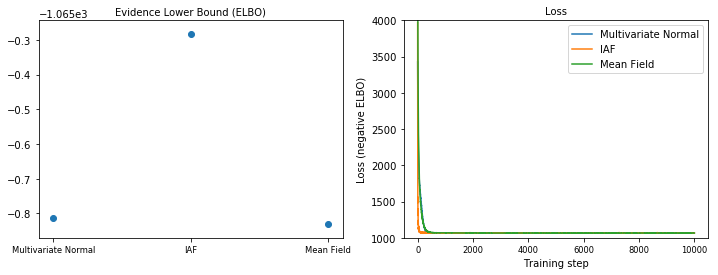
Нижняя граница доказательств (ELBO)
IAF, безусловно, самый большой и самый гибкий суррогатный апериод, сходится к наивысшей доказательной нижней границе (ELBO).
plot_loss_and_elbo()
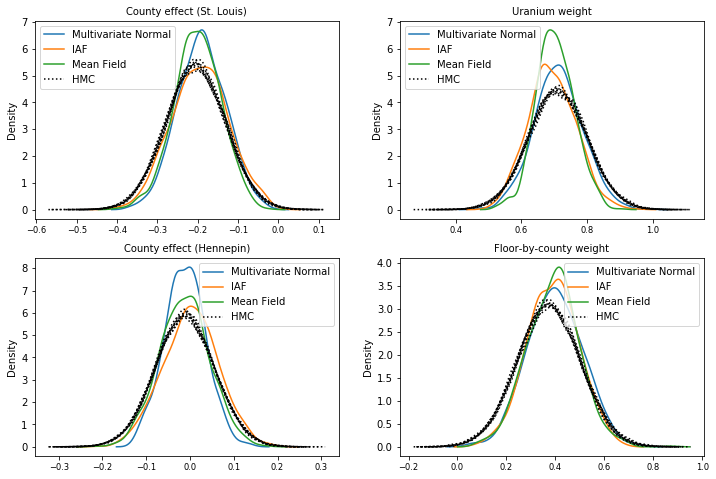
Задние образцы
Выборки из каждой суррогатной апостериорной оценки по сравнению с наземными образцами HMC (различная визуализация образцов, показанная на прямоугольных диаграммах).
plot_kdes()
Вывод
В этом Colab мы построили суррогатные апостериорные VI VI, используя совместные распределения и составные бижекторы, и подогнали их для оценки достоверных интервалов для весов в регрессионной модели на наборе данных радона. Для этой простой модели более выразительные суррогатные задние зубы выполняются аналогично суррогатным задним значениям среднего поля. Однако продемонстрированные нами инструменты можно использовать для создания широкого спектра гибких суррогатных задних зубов, подходящих для более сложных моделей.
