 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Tutorial ini menunjukkan bagaimana jaringan saraf klasik dapat belajar untuk memperbaiki kesalahan kalibrasi qubit. Ini memperkenalkan Cirq , kerangka kerja Python untuk membuat, mengedit, dan menjalankan sirkuit Noisy Intermediate Scale Quantum (NISQ), dan menunjukkan bagaimana Cirq berinteraksi dengan TensorFlow Quantum.
Mempersiapkan
pip install tensorflow==2.7.0
Instal TensorFlow Quantum:
pip install tensorflow-quantum
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.7/site-packages/pkg_resources/__init__.py'>
Sekarang impor TensorFlow dan dependensi modul:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2022-02-04 12:27:31.677071: E tensorflow/stream_executor/cuda/cuda_driver.cc:271] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. Dasar-dasarnya
1.1 Cirq dan sirkuit kuantum berparameter
Sebelum menjelajahi TensorFlow Quantum (TFQ), mari kita lihat beberapa dasar Cirq . Cirq adalah pustaka Python untuk komputasi kuantum dari Google. Anda menggunakannya untuk mendefinisikan sirkuit, termasuk gerbang statis dan parameter.
Cirq menggunakan simbol SymPy untuk mewakili parameter gratis.
a, b = sympy.symbols('a b')
Kode berikut membuat sirkuit dua-qubit menggunakan parameter Anda:
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
Untuk mengevaluasi sirkuit, Anda dapat menggunakan antarmuka cirq.Simulator . Anda mengganti parameter bebas di sirkuit dengan nomor tertentu dengan mengirimkan objek cirq.ParamResolver . Kode berikut menghitung output vektor keadaan mentah dari sirkuit berparameter Anda:
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
Vektor keadaan tidak dapat diakses secara langsung di luar simulasi (perhatikan bilangan kompleks pada keluaran di atas). Agar realistis secara fisik, Anda harus menentukan pengukuran, yang mengubah vektor keadaan menjadi bilangan real yang dapat dipahami oleh komputer klasik. Cirq menentukan pengukuran menggunakan kombinasi operator Pauli \(\hat{X}\), \(\hat{Y}\), dan \(\hat{Z}\). Sebagai ilustrasi, kode berikut mengukur \(\hat{Z}_0\) dan \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\) pada vektor status yang baru saja Anda simulasikan:
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 Sirkuit kuantum sebagai tensor
TensorFlow Quantum (TFQ) menyediakan tfq.convert_to_tensor , sebuah fungsi yang mengubah objek Cirq menjadi tensor. Ini memungkinkan Anda mengirim objek Cirq ke lapisan kuantum dan operasi kuantum kami. Fungsi tersebut dapat dipanggil pada daftar atau larik Sirkuit Cirq dan Cirq Paulis:
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
Ini mengkodekan objek Cirq sebagai tensor tf.string yang didekodekan oleh operasi tfq sesuai kebutuhan.
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 Simulasi rangkaian batching
TFQ menyediakan metode untuk menghitung nilai harapan, sampel, dan vektor keadaan. Untuk saat ini, mari kita fokus pada nilai ekspektasi .
Antarmuka tingkat tertinggi untuk menghitung nilai ekspektasi adalah lapisan tfq.layers.Expectation , yang merupakan tf.keras.Layer . Dalam bentuknya yang paling sederhana, lapisan ini setara dengan mensimulasikan sirkuit berparameter pada banyak cirq.ParamResolvers ; namun, TFQ memungkinkan pengelompokan mengikuti semantik TensorFlow, dan sirkuit disimulasikan menggunakan kode C++ yang efisien.
Buat kumpulan nilai untuk menggantikan parameter a dan b kami:
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=np.float32)
Eksekusi sirkuit batch pada nilai parameter di Cirq membutuhkan loop:
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[-0.66652703] [ 0.49764055] [ 0.67326665] [-0.95549959] [-0.81297827]]
Operasi yang sama disederhanakan dalam TFQ:
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[-0.666526 ],
[ 0.49764216],
[ 0.6732664 ],
[-0.9554999 ],
[-0.8129788 ]], dtype=float32)>
2. Optimalisasi kuantum-klasik hibrida
Sekarang setelah Anda melihat dasar-dasarnya, mari gunakan TensorFlow Quantum untuk membangun jaringan saraf klasik kuantum hibrida . Anda akan melatih jaringan saraf klasik untuk mengontrol satu qubit. Kontrol akan dioptimalkan untuk mempersiapkan qubit dengan benar dalam keadaan 0 atau 1 , mengatasi kesalahan kalibrasi sistematis yang disimulasikan. Gambar ini menunjukkan arsitektur:
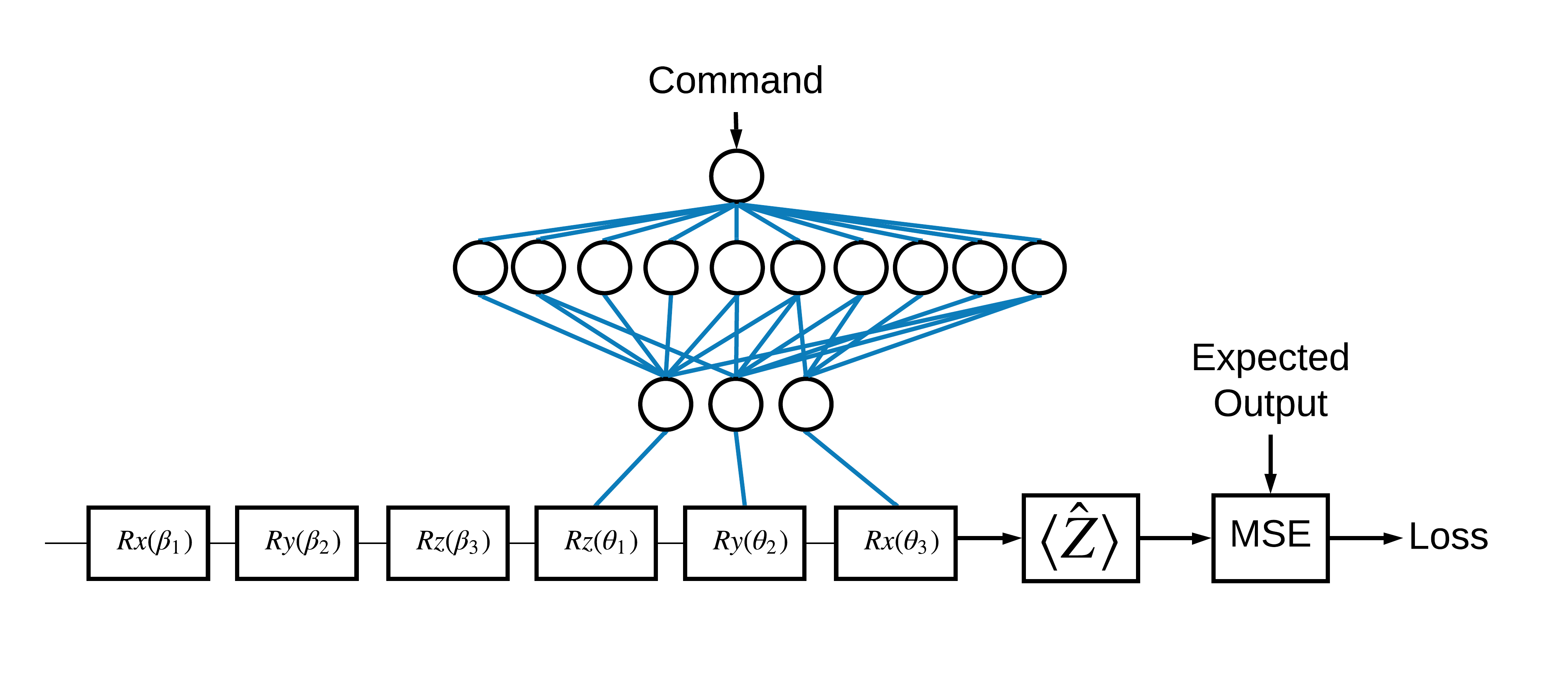
Bahkan tanpa jaringan saraf, ini adalah masalah yang mudah dipecahkan, tetapi temanya mirip dengan masalah kontrol kuantum nyata yang mungkin Anda selesaikan menggunakan TFQ. Ini menunjukkan contoh end-to-end komputasi kuantum klasik menggunakan lapisan tfq.layers.ControlledPQC (Parametrized Quantum Circuit) di dalam tf.keras.Model .
Untuk implementasi tutorial ini, arsitektur ini dibagi menjadi 3 bagian:
- Sirkuit input atau sirkuit titik data : Tiga gerbang \(R\) pertama.
- Sirkuit terkontrol : Tiga gerbang \(R\) lainnya.
- Pengontrol : Jaringan saraf klasik mengatur parameter sirkuit yang dikontrol.
2.1 Definisi sirkuit terkontrol
Tentukan rotasi bit tunggal yang dapat dipelajari, seperti yang ditunjukkan pada gambar di atas. Ini akan sesuai dengan sirkuit terkontrol kami.
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
2.2 Pengontrol
Sekarang tentukan jaringan pengontrol:
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Diberikan sekumpulan perintah, pengontrol mengeluarkan sekumpulan sinyal kontrol untuk rangkaian yang dikendalikan.
Pengontrol diinisialisasi secara acak sehingga keluaran ini belum berguna.
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[0. , 0. , 0. ],
[0.5815686 , 0.21376055, 0.57181627]], dtype=float32)
2.3 Hubungkan pengontrol ke sirkuit
Gunakan tfq untuk menghubungkan pengontrol ke sirkuit yang dikontrol, sebagai satu keras.Model .
Lihat panduan API Fungsional Keras untuk mengetahui lebih lanjut tentang gaya definisi model ini.
Pertama-tama tentukan input ke model:
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
Selanjutnya terapkan operasi pada input tersebut, untuk menentukan komputasinya.
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
Sekarang paketkan komputasi ini sebagai tf.keras.Model :
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
Arsitektur jaringan ditunjukkan oleh plot model di bawah ini. Bandingkan plot model ini dengan diagram arsitektur untuk memverifikasi kebenarannya.
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
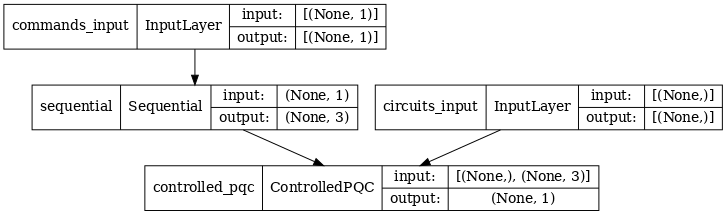
Model ini mengambil dua input: Perintah untuk pengontrol, dan sirkuit input yang outputnya coba diperbaiki oleh pengontrol.
2.4 kumpulan data
Model mencoba untuk menampilkan nilai pengukuran yang benar dari \(\hat{Z}\) untuk setiap perintah. Perintah dan nilai yang benar didefinisikan di bawah ini.
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
Ini bukan keseluruhan dataset pelatihan untuk tugas ini. Setiap titik data dalam kumpulan data juga membutuhkan sirkuit input.
2.4 Definisi sirkuit input
Sirkuit input di bawah ini mendefinisikan kesalahan kalibrasi acak yang akan dipelajari model untuk dikoreksi.
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
Ada dua salinan sirkuit, satu untuk setiap titik data.
datapoint_circuits.shape
TensorShape([2])
2.5 Pelatihan
Dengan input yang ditentukan, Anda dapat menguji-menjalankan model tfq .
model([datapoint_circuits, commands]).numpy()
array([[0.95853525],
[0.6272128 ]], dtype=float32)
Sekarang jalankan proses pelatihan standar untuk menyesuaikan nilai-nilai ini ke expected_outputs .
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
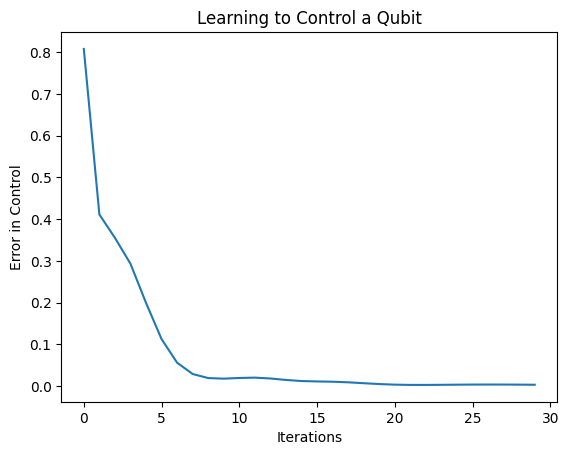
Dari plot ini Anda dapat melihat bahwa jaringan saraf telah belajar untuk mengatasi kesalahan kalibrasi yang sistematis.
2.6 Verifikasi keluaran
Sekarang gunakan model terlatih, untuk memperbaiki kesalahan kalibrasi qubit. Dengan Cirq:
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [-0.6788422 0.3395225 -0.59394693] Which gives an actual expectation of: 0.9171845316886902 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-5.203663 -0.29528576 3.2887425 ] Which gives an actual expectation of: -0.9511058330535889
Nilai fungsi kerugian selama pelatihan memberikan gambaran kasar tentang seberapa baik model belajar. Semakin rendah kerugiannya, semakin dekat nilai ekspektasi dalam sel di atas dengan desired_values . Jika Anda tidak terlalu peduli dengan nilai parameter, Anda selalu dapat memeriksa output dari atas menggunakan tfq :
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.91718477],
[-0.9511056 ]], dtype=float32)>
3 Belajar menyiapkan eigenstate dari operator yang berbeda
Pilihan eigenstate \(\pm \hat{Z}\) sesuai dengan 1 dan 0 adalah arbitrer. Anda dapat dengan mudah menginginkan 1 sesuai dengan \(+ \hat{Z}\) eigenstate dan 0 sesuai dengan \(-\hat{X}\) eigenstate. Salah satu cara untuk mencapai ini adalah dengan menentukan operator pengukuran yang berbeda untuk setiap perintah, seperti yang ditunjukkan pada gambar di bawah ini:
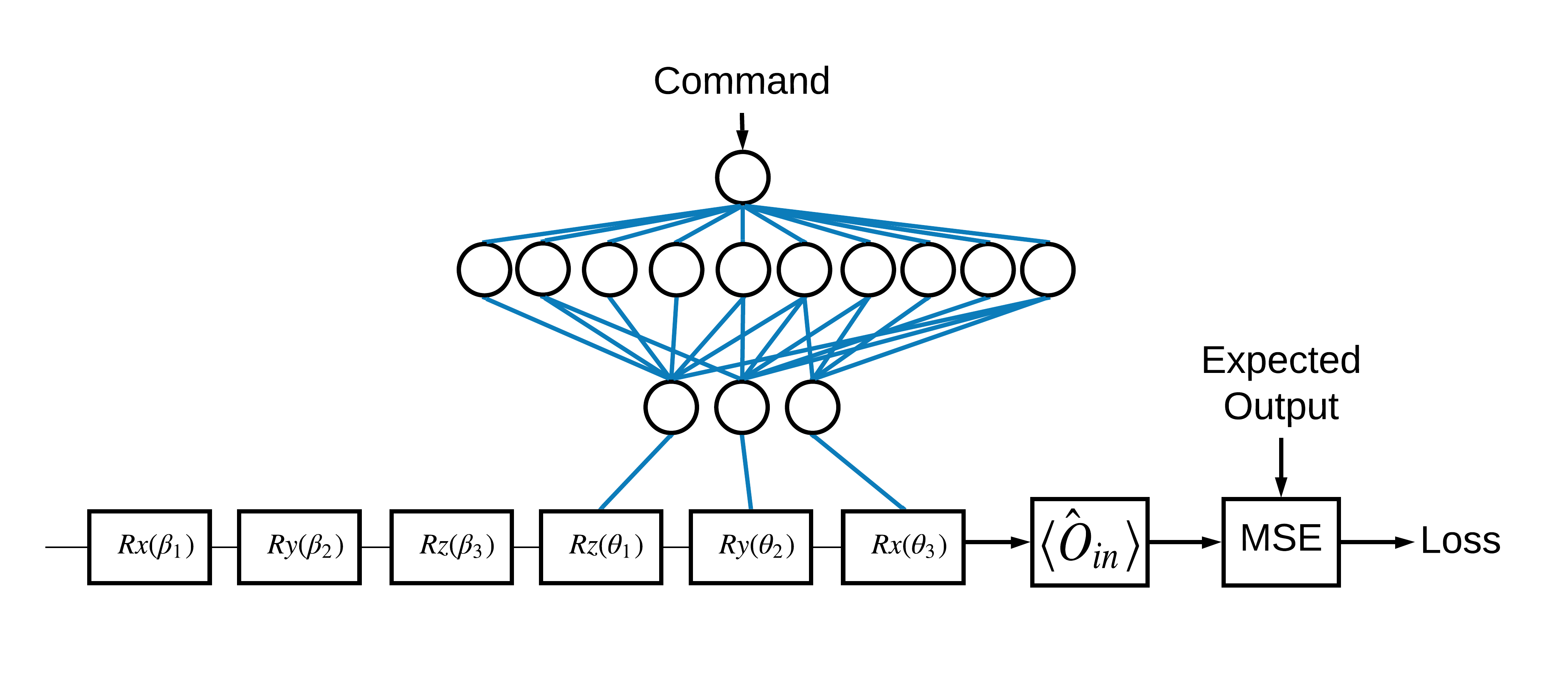
Ini membutuhkan penggunaan tfq.layers.Expectation . Sekarang input Anda telah berkembang menjadi tiga objek: sirkuit, perintah, dan operator. Outputnya masih nilai harapan.
3.1 Definisi model baru
Mari kita lihat model untuk menyelesaikan tugas ini:
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
Berikut adalah jaringan pengontrol:
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
Gabungkan sirkuit dan pengontrol menjadi satu keras.Model menggunakan tfq :
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 Kumpulan data
Sekarang Anda juga akan menyertakan operator yang ingin Anda ukur untuk setiap titik data yang Anda berikan untuk model_circuit :
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 Pelatihan
Sekarang setelah Anda memiliki input dan output baru, Anda dapat melatih sekali lagi menggunakan keras.
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 320ms/step - loss: 2.4404 Epoch 2/30 1/1 [==============================] - 0s 3ms/step - loss: 1.8713 Epoch 3/30 1/1 [==============================] - 0s 3ms/step - loss: 1.1400 Epoch 4/30 1/1 [==============================] - 0s 3ms/step - loss: 0.5071 Epoch 5/30 1/1 [==============================] - 0s 3ms/step - loss: 0.1611 Epoch 6/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0426 Epoch 7/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0117 Epoch 8/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0032 Epoch 9/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0147 Epoch 10/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0452 Epoch 11/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0670 Epoch 12/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0648 Epoch 13/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0471 Epoch 14/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0289 Epoch 15/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0180 Epoch 16/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0138 Epoch 17/30 1/1 [==============================] - 0s 2ms/step - loss: 0.0130 Epoch 18/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0137 Epoch 19/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0148 Epoch 20/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0156 Epoch 21/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0157 Epoch 22/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0149 Epoch 23/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0135 Epoch 24/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0119 Epoch 25/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0100 Epoch 26/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0082 Epoch 27/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0064 Epoch 28/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0047 Epoch 29/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0034 Epoch 30/30 1/1 [==============================] - 0s 3ms/step - loss: 0.0024
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
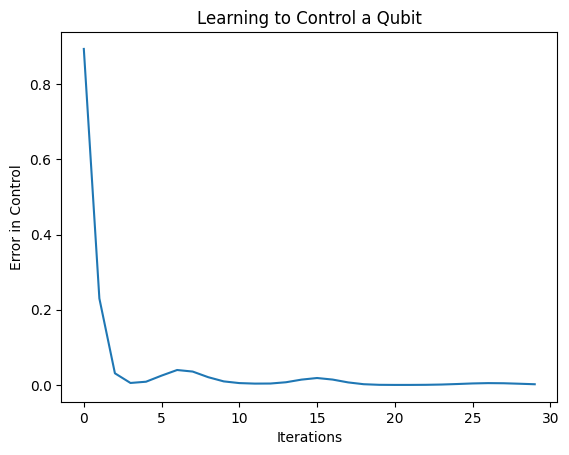
Fungsi kerugian telah turun ke nol.
controller tersedia sebagai model yang berdiri sendiri. Panggil pengontrol, dan periksa responsnya terhadap setiap sinyal perintah. Perlu beberapa upaya untuk membandingkan output ini dengan benar dengan konten random_rotations .
controller.predict(np.array([0,1]))
array([[3.6335812 , 1.8470774 , 0.71675825],
[5.3085413 , 0.08116499, 2.8337662 ]], dtype=float32)
