TensorFlow Lattice là một thư viện triển khai các mô hình dựa trên mạng linh hoạt, có thể kiểm soát và có thể giải thích được. Thư viện cho phép bạn đưa kiến thức về miền vào quá trình học tập thông qua các ràng buộc về hình dạng theo lẽ thường hoặc theo định hướng chính sách . Điều này được thực hiện bằng cách sử dụng một tập hợp các lớp Keras có thể đáp ứng các ràng buộc như tính đơn điệu, độ lồi và độ tin cậy theo cặp. Thư viện cũng cung cấp các mô hình được tạo sẵn dễ dàng cài đặt.
Khái niệm
Phần này là phiên bản đơn giản của mô tả trong Bảng tra cứu nội suy được hiệu chỉnh đơn điệu , JMLR 2016.
Lưới
Mạng là một bảng tra cứu nội suy có thể ước chừng các mối quan hệ đầu vào-đầu ra tùy ý trong dữ liệu của bạn. Nó chồng lưới thông thường lên không gian đầu vào của bạn và tìm hiểu các giá trị cho đầu ra ở các đỉnh của lưới. Đối với điểm kiểm tra \(x\), \(f(x)\) được nội suy tuyến tính từ các giá trị mạng xung quanh \(x\).
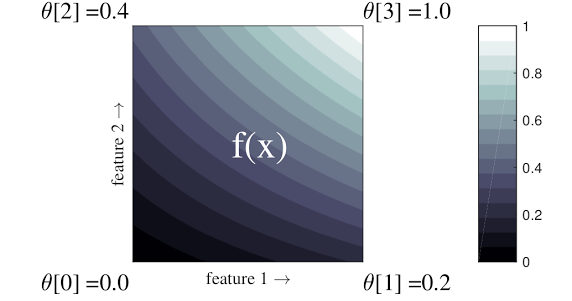
Ví dụ đơn giản ở trên là một hàm có 2 tính năng đầu vào và 4 tham số:\(\theta=[0, 0.2, 0.4, 1]\), là các giá trị của hàm ở các góc của không gian đầu vào; phần còn lại của hàm được nội suy từ các tham số này.
chức năng \(f(x)\) có thể nắm bắt các tương tác phi tuyến tính giữa các tính năng. Bạn có thể coi các tham số mạng là chiều cao của các cực đặt trên mặt đất trên một lưới thông thường và hàm thu được giống như tấm vải được kéo chặt vào bốn cực.
Với \(D\) các đặc điểm và 2 đỉnh dọc theo mỗi chiều, một mạng thông thường sẽ có \(2^D\) các thông số. Để phù hợp với một hàm linh hoạt hơn, bạn có thể chỉ định một mạng tinh vi hơn trên không gian đặc trưng với nhiều đỉnh hơn dọc theo mỗi chiều. Hàm hồi quy mạng là hàm liên tục và có khả vi vô hạn từng phần.
Sự định cỡ
Giả sử mạng mẫu trước biểu thị mức độ hài lòng của người dùng đã học với một quán cà phê địa phương được đề xuất được tính toán bằng các tính năng:
- giá cà phê, trong khoảng từ 0 đến 20 đô la
- khoảng cách tới người dùng, trong phạm vi 0 đến 30 km
Chúng tôi muốn mô hình của mình tìm hiểu mức độ hài lòng của người dùng với đề xuất quán cà phê địa phương. Các mô hình TensorFlow Lattice có thể sử dụng các hàm tuyến tính từng phần (với tfl.layers.PWLCalibration ) để hiệu chỉnh và chuẩn hóa các tính năng đầu vào theo phạm vi được mạng chấp nhận: 0,0 đến 1,0 trong mạng ví dụ ở trên. Các ví dụ sau đây hiển thị các chức năng hiệu chỉnh như vậy với 10 điểm chính:
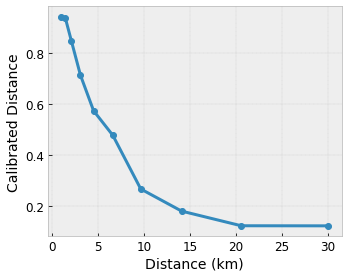
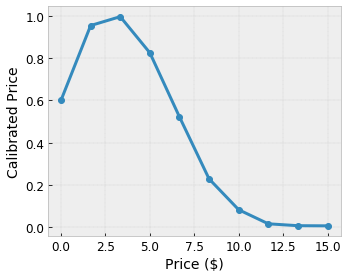
Thông thường, nên sử dụng các lượng tử của các đặc điểm làm điểm chính đầu vào. Các mô hình tạo sẵn của TensorFlow Lattice có thể tự động đặt các điểm khóa đầu vào thành các lượng tử tính năng.
Đối với các tính năng phân loại, TensorFlow Lattice cung cấp hiệu chuẩn phân loại (với tfl.layers.CategoricalCalibration ) với giới hạn đầu ra tương tự để đưa vào một mạng.
hòa tấu
Số lượng tham số của lớp mạng tăng theo cấp số nhân với số lượng tính năng đầu vào, do đó không thể mở rộng tốt đến các kích thước rất cao. Để khắc phục hạn chế này, TensorFlow Lattice cung cấp các nhóm mạng kết hợp (trung bình) một số mạng nhỏ , cho phép mô hình phát triển tuyến tính về số lượng tính năng.
Thư viện cung cấp hai biến thể của các nhóm này:
Lưới nhỏ ngẫu nhiên (RTL): Mỗi mô hình con sử dụng một tập hợp con các tính năng ngẫu nhiên (có thay thế).
Crystals : Thuật toán Crystals trước tiên huấn luyện một mô hình tiền trang bị để ước tính các tương tác tính năng theo cặp. Sau đó, nó sắp xếp quần thể cuối cùng sao cho các đặc điểm có nhiều tương tác phi tuyến tính hơn nằm trong cùng một mạng.
Tại sao mạng TensorFlow?
Bạn có thể tìm thấy phần giới thiệu ngắn gọn về TensorFlow Lattice trong bài đăng trên Blog TF này.
Khả năng giải thích
Vì các tham số của mỗi lớp là đầu ra của lớp đó nên rất dễ phân tích, hiểu và gỡ lỗi từng phần của mô hình.
Mô hình chính xác và linh hoạt
Sử dụng các mạng tinh thể, bạn có thể nhận được các hàm phức tạp tùy ý chỉ với một lớp mạng. Việc sử dụng nhiều lớp bộ hiệu chuẩn và mạng thường hoạt động hiệu quả trong thực tế và có thể phù hợp hoặc hoạt động tốt hơn các mô hình DNN có kích thước tương tự.
Các ràng buộc hình dạng thông thường
Dữ liệu đào tạo trong thế giới thực có thể không thể hiện đầy đủ dữ liệu thời gian chạy. Các giải pháp ML linh hoạt như DNN hoặc rừng thường hoạt động bất ngờ và thậm chí dữ dội ở những phần không gian đầu vào không có trong dữ liệu huấn luyện. Hành vi này đặc biệt có vấn đề khi các ràng buộc về chính sách hoặc sự công bằng có thể bị vi phạm.
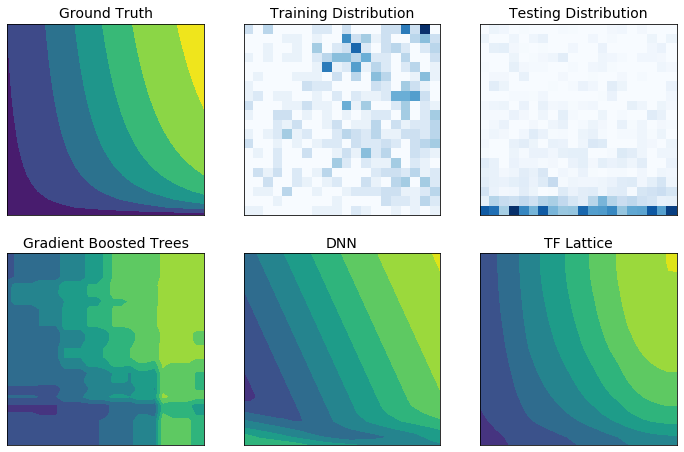
Mặc dù các hình thức chính quy hóa phổ biến có thể dẫn đến phép ngoại suy hợp lý hơn, nhưng các bộ điều chỉnh tiêu chuẩn không thể đảm bảo hành vi mô hình hợp lý trên toàn bộ không gian đầu vào, đặc biệt là với đầu vào nhiều chiều. Việc chuyển sang các mô hình đơn giản hơn với hành vi được kiểm soát và dự đoán tốt hơn có thể phải trả giá đắt cho độ chính xác của mô hình.
TF Lattice cho phép tiếp tục sử dụng các mô hình linh hoạt nhưng cung cấp một số tùy chọn để đưa kiến thức miền vào quá trình học tập thông qua các ràng buộc hình dạng theo chính sách hoặc theo ý nghĩa chung có ý nghĩa về mặt ngữ nghĩa:
- Tính đơn điệu : Bạn có thể chỉ định rằng đầu ra chỉ nên tăng/giảm so với đầu vào. Trong ví dụ của chúng tôi, bạn có thể muốn chỉ định rằng khoảng cách tăng lên đến quán cà phê sẽ chỉ làm giảm sở thích được dự đoán của người dùng.
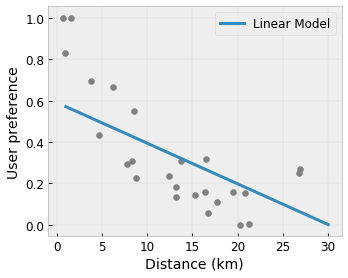
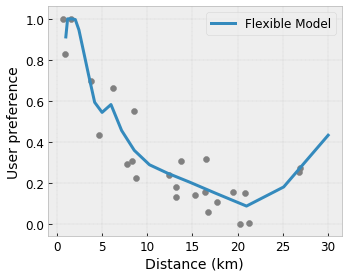
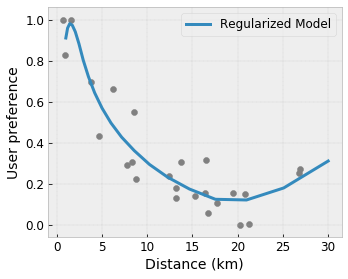
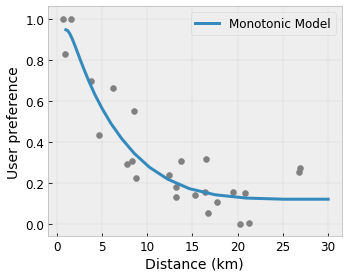
Convexity/Concavity : Bạn có thể chỉ định rằng hình dạng hàm có thể lồi hoặc lõm. Kết hợp với tính đơn điệu, điều này có thể buộc hàm biểu thị hiệu suất giảm dần đối với một tính năng nhất định.
Tính đơn thức : Bạn có thể chỉ định rằng hàm phải có một đỉnh hoặc một đáy duy nhất. Điều này cho phép bạn biểu diễn các hàm có điểm phù hợp đối với một tính năng.
Tin cậy theo cặp : Ràng buộc này hoạt động trên một cặp tính năng và gợi ý rằng một tính năng đầu vào phản ánh về mặt ngữ nghĩa sự tin cậy vào tính năng khác. Ví dụ: số lượng đánh giá cao hơn khiến bạn tự tin hơn vào xếp hạng sao trung bình của một nhà hàng. Mô hình sẽ nhạy hơn đối với xếp hạng sao (tức là sẽ có độ dốc lớn hơn đối với xếp hạng) khi số lượng đánh giá cao hơn.
Tính linh hoạt được kiểm soát với bộ điều chỉnh
Ngoài các ràng buộc về hình dạng, mạng TensorFlow còn cung cấp một số bộ điều chỉnh để kiểm soát tính linh hoạt và độ mượt mà của chức năng cho mỗi lớp.
Bộ điều chỉnh Laplacian : Đầu ra của các đỉnh/điểm khóa mạng/hiệu chuẩn được chính quy hóa theo các giá trị của các lân cận tương ứng của chúng. Điều này dẫn đến một chức năng phẳng hơn .
Hessian Regularizer : Điều này xử phạt đạo hàm đầu tiên của lớp hiệu chỉnh PWL để làm cho hàm tuyến tính hơn .
Wrinkle Regularizer : Điều này xử phạt đạo hàm thứ hai của lớp hiệu chuẩn PWL để tránh những thay đổi đột ngột về độ cong. Nó làm cho chức năng mượt mà hơn.
Bộ điều chỉnh độ xoắn : Đầu ra của mạng sẽ được điều chỉnh theo hướng ngăn chặn độ xoắn giữa các đối tượng địa lý. Nói cách khác, mô hình sẽ được chính quy hóa theo hướng độc lập giữa sự đóng góp của các đặc trưng.
Trộn và kết hợp với các lớp Keras khác
Bạn có thể sử dụng các lớp TF Lattice kết hợp với các lớp Keras khác để xây dựng các mô hình bị ràng buộc một phần hoặc được chuẩn hóa một phần. Ví dụ: các lớp hiệu chuẩn mạng hoặc PWL có thể được sử dụng ở lớp cuối cùng của các mạng sâu hơn bao gồm các phần nhúng hoặc các lớp Keras khác.
giấy tờ
- Đạo đức nghĩa vụ theo những ràng buộc hình dạng đơn điệu , Serena Wang, Maya Gupta, Hội nghị quốc tế về trí tuệ nhân tạo và thống kê (AISTATS), 2020
- Ràng buộc hình dạng cho các hàm tập hợp , Andrew Cotter, Maya Gupta, H. Jiang, Erez Louidor, Jim Muller, Taman Narayan, Serena Wang, Tao Zhu. Hội nghị quốc tế về học máy (ICML), 2019
- Lợi nhuận giảm dần Các hạn chế về hình dạng đối với khả năng diễn giải và chính quy hóa , Maya Gupta, Dara Bahri, Andrew Cotter, Kevin Canini, Những tiến bộ trong hệ thống xử lý thông tin thần kinh (NeurIPS), 2018
- Mạng lưới sâu và các hàm đơn điệu từng phần , Seungil You, Kevin Canini, David Ding, Jan Pfeifer, Maya R. Gupta, Những tiến bộ trong hệ thống xử lý thông tin thần kinh (NeurIPS), 2017
- Các hàm đơn điệu nhanh và linh hoạt với các tập hợp mạng , Mahdi Milani Fard, Kevin Canini, Andrew Cotter, Jan Pfeifer, Maya Gupta, Những tiến bộ trong hệ thống xử lý thông tin thần kinh (NeurIPS), 2016
- Bảng tra cứu nội suy được hiệu chỉnh đơn điệu , Maya Gupta, Andrew Cotter, Jan Pfeifer, Konstantin Voevodski, Kevin Canini, Alexander Mangylov, Wojciech Moczydlowski, Alexander van Esbroeck, Tạp chí Nghiên cứu Máy học (JMLR), 2016
- Hồi quy được tối ưu hóa để đánh giá chức năng hiệu quả , Eric Garcia, Raman Arora, Maya R. Gupta, Giao dịch của IEEE về xử lý hình ảnh, 2012
- Hồi quy mạng , Eric Garcia, Maya Gupta, Những tiến bộ trong hệ thống xử lý thông tin thần kinh (NeurIPS), 2009
Hướng dẫn và tài liệu API
Đối với các kiến trúc mô hình phổ biến, bạn có thể sử dụng các mô hình tạo sẵn của Keras . Bạn cũng có thể tạo các mô hình tùy chỉnh bằng cách sử dụng các lớp TF Lattice Keras hoặc trộn và kết hợp với các lớp Keras khác. Hãy xem tài liệu API đầy đủ để biết chi tiết.

