 TensorFlow.org에서 보기 TensorFlow.org에서 보기 |
 Google Colab에서 실행하기 Google Colab에서 실행하기 |
 GitHub에서 보기 GitHub에서 보기 |
 노트북 다운로드하기 노트북 다운로드하기 |
8개 학교 문제(The eight schools problem)(Rubin 1981)는 8개 학교에서 동시에 수행되는 SAT 코칭 프로그램의 효과를 고려하는 문제입니다. 이는 교환 가능한 그룹 간에 정보를 공유하기 위한 계층적 모델링의 유용성을 보여주는 고전적인 문제(Bayesian Data Analysis, Stan)가 되었습니다.
아래 구현은 Edward 1.0 튜토리얼을 수정한 것입니다.
가져오기
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
import warnings
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
데이터
베이지안 데이터 분석, 5.5 섹션(Gelman 외, 2013)은 다음과 같습니다.
각 8개 고등학교에서 SAT-V(Scholastic Aptitude Test-Verbal)에 대한 특수 코칭 프로그램의 효과를 분석하기 위해 교육 테스트 서비스를 위한 연구가 수행되었습니다. 각 연구의 결과 변수는 SAT-V의 특별 관리 점수로, 교육 시험 서비스에서 관리하고 대학의 입학 결정을 돕는 데 사용되는 표준화된 객관식 시험입니다. 점수는 200에서 800까지 다양하며 평균은 약 500, 표준 편차는 약 100입니다. SAT 시험은 특히 시험 성적 향상을 위한 단기적인 노력에 저항하도록 설계되었습니다. 대신 이들 시험은 수년간의 교육을 통해 습득한 지식과 개발된 능력을 반영하도록 설계되었습니다. 그런데도 이 연구에 참여한 각각의 8개 학교는 단기 코칭 프로그램이 SAT 점수를 높이는 데 매우 성공적이라고 생각했습니다. 또한 8개 프로그램 중 어떤 것이 다른 프로그램보다 더 효과적이거나 어떤 프로그램이 다른 프로그램보다 효과가 더 유사하다고 믿을만한 선행 사유가 없었습니다.
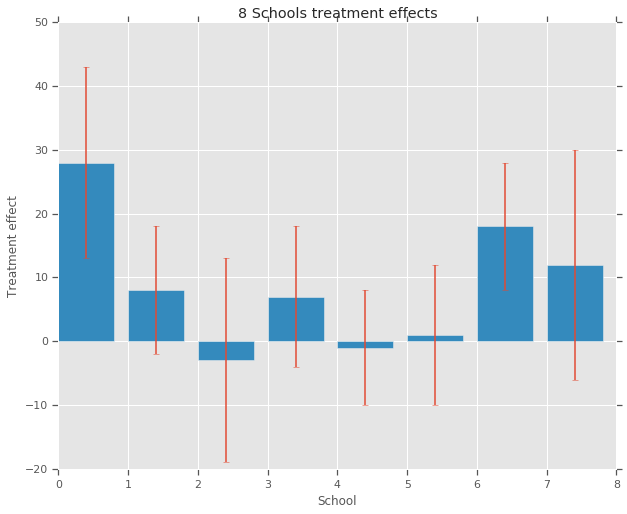
각 8개 학교(\(J = 8\))에 대해 추정된 처치 효과 \(y_j\)와 효과 추정치 \(\sigma_j\)의 표준 오차가 있습니다. 이 연구에서 처치 효과는 PSAT-M 및 PSAT-V 점수를 통제 변수로 사용하여 처치 집단에 대한 선형 회귀를 통해 얻었습니다. 어느 학교가 서로 어느 정도 유사하거나, 어떤 코칭 프로그램이 더 효과적일 것이라는 기존 믿음이 없었으므로 처치 효과를 교환 가능한 것으로 간주할 수 있습니다.
num_schools = 8 # number of schools
treatment_effects = np.array(
[28, 8, -3, 7, -1, 1, 18, 12], dtype=np.float32) # treatment effects
treatment_stddevs = np.array(
[15, 10, 16, 11, 9, 11, 10, 18], dtype=np.float32) # treatment SE
fig, ax = plt.subplots()
plt.bar(range(num_schools), treatment_effects, yerr=treatment_stddevs)
plt.title("8 Schools treatment effects")
plt.xlabel("School")
plt.ylabel("Treatment effect")
fig.set_size_inches(10, 8)
plt.show()
모델
데이터를 캡처하기 위해 계층적 정규 모델을 사용합니다. 다음의 생성 과정을 따릅니다.
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \ \text{for } & i=1\ldots 8:\ & \theta_i \sim \text{Normal}\left(\text{loc}{=}\mu,\ \text{scale}{=}\tau \right) \ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
여기서 \(\mu\)는 이전 평균 처치 효과를 나타내며 \(\tau\)는 학교 간의 분산을 제어합니다. \(y_i\) 및 \(\sigma_i\)가 관찰됩니다. \(\tau \rightarrow \infty\)로 모델은 풀링 없음 모델에 접근합니다. 즉, 각 학교 처치 효과 추정치가 더 독립적일 수 있습니다. \(\tau \rightarrow 0\)로 모델은 완전 풀링 모델에 접근합니다. 즉, 모든 학교 처치 효과가 그룹 평균 \(\mu\)에 더 가깝습니다. 표준 편차를 양수로 제한하기 위해 로그 정규 분포에서 \(\tau\)를 그립니다(정규 분포에서 \(\log(\tau)\)를 그리는 것과 동일함).
발산(divergence)을 사용한 바이어스 추론 진단에 따라 위의 모델을 동등한 비 중심 모델로 변환합니다.
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \ \text{for } & i=1\ldots 8:\ & \theta_i' \sim \text{Normal}\left(\text{loc}{=}0,\ \text{scale}{=}1 \right) \ & \theta_i = \mu + \tau \theta_i' \ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
이 모델을 JointDistributionSequential 인스턴스로 실체화합니다.
model = tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=10., name="avg_effect"), # `mu` above
tfd.Normal(loc=5., scale=1., name="avg_stddev"), # `log(tau)` above
tfd.Independent(tfd.Normal(loc=tf.zeros(num_schools),
scale=tf.ones(num_schools),
name="school_effects_standard"), # `theta_prime`
reinterpreted_batch_ndims=1),
lambda school_effects_standard, avg_stddev, avg_effect: (
tfd.Independent(tfd.Normal(loc=(avg_effect[..., tf.newaxis] +
tf.exp(avg_stddev[..., tf.newaxis]) *
school_effects_standard), # `theta` above
scale=treatment_stddevs),
name="treatment_effects", # `y` above
reinterpreted_batch_ndims=1))
])
def target_log_prob_fn(avg_effect, avg_stddev, school_effects_standard):
"""Unnormalized target density as a function of states."""
return model.log_prob((
avg_effect, avg_stddev, school_effects_standard, treatment_effects))
베이지안 추론
주어진 데이터에서 해밀턴 몬테카를로(HMC)를 수행하여 모델의 매개변수에 대한 사후 확률 분포를 계산합니다.
num_results = 5000
num_burnin_steps = 3000
# Improve performance by tracing the sampler using `tf.function`
# and compiling it using XLA.
@tf.function(autograph=False, experimental_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
tf.zeros([], name='init_avg_effect'),
tf.zeros([], name='init_avg_stddev'),
tf.ones([num_schools], name='init_school_effects_standard'),
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.4,
num_leapfrog_steps=3))
states, kernel_results = do_sampling()
avg_effect, avg_stddev, school_effects_standard = states
school_effects_samples = (
avg_effect[:, np.newaxis] +
np.exp(avg_stddev)[:, np.newaxis] * school_effects_standard)
num_accepted = np.sum(kernel_results.is_accepted)
print('Acceptance rate: {}'.format(num_accepted / num_results))
Acceptance rate: 0.5974
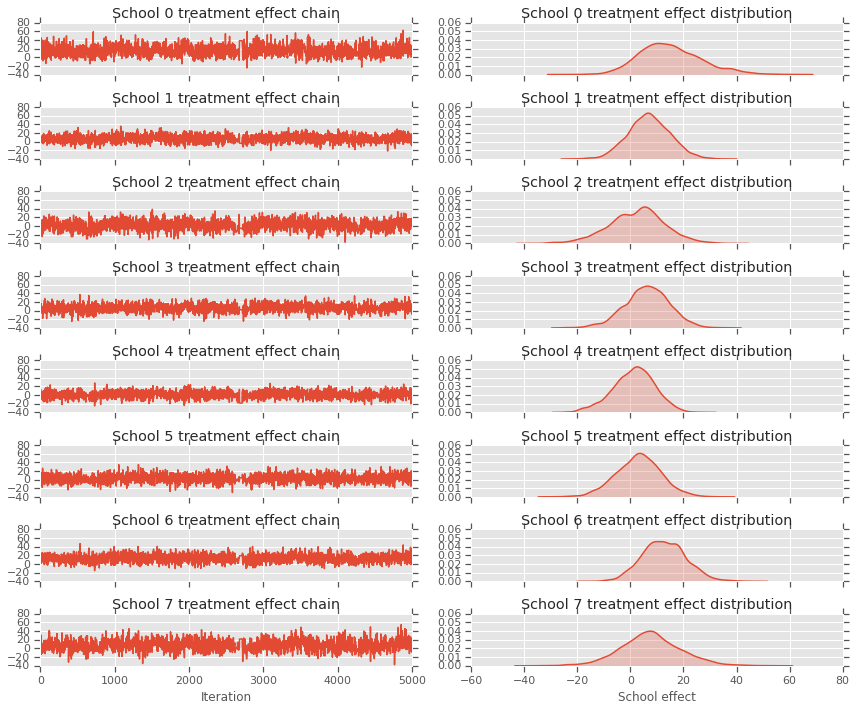
fig, axes = plt.subplots(8, 2, sharex='col', sharey='col')
fig.set_size_inches(12, 10)
for i in range(num_schools):
axes[i][0].plot(school_effects_samples[:,i].numpy())
axes[i][0].title.set_text("School {} treatment effect chain".format(i))
sns.kdeplot(school_effects_samples[:,i].numpy(), ax=axes[i][1], shade=True)
axes[i][1].title.set_text("School {} treatment effect distribution".format(i))
axes[num_schools - 1][0].set_xlabel("Iteration")
axes[num_schools - 1][1].set_xlabel("School effect")
fig.tight_layout()
plt.show()
print("E[avg_effect] = {}".format(np.mean(avg_effect)))
print("E[avg_stddev] = {}".format(np.mean(avg_stddev)))
print("E[school_effects_standard] =")
print(np.mean(school_effects_standard[:, ]))
print("E[school_effects] =")
print(np.mean(school_effects_samples[:, ], axis=0))
E[avg_effect] = 5.57183933258 E[avg_stddev] = 2.47738981247 E[school_effects_standard] = 0.08509017 E[school_effects] = [15.0051 7.103311 2.4552586 6.2744603 1.3364682 3.1125953 12.762501 7.743602 ]
# Compute the 95% interval for school_effects
school_effects_low = np.array([
np.percentile(school_effects_samples[:, i], 2.5) for i in range(num_schools)
])
school_effects_med = np.array([
np.percentile(school_effects_samples[:, i], 50) for i in range(num_schools)
])
school_effects_hi = np.array([
np.percentile(school_effects_samples[:, i], 97.5)
for i in range(num_schools)
])
fig, ax = plt.subplots(nrows=1, ncols=1, sharex=True)
ax.scatter(np.array(range(num_schools)), school_effects_med, color='red', s=60)
ax.scatter(
np.array(range(num_schools)) + 0.1, treatment_effects, color='blue', s=60)
plt.plot([-0.2, 7.4], [np.mean(avg_effect),
np.mean(avg_effect)], 'k', linestyle='--')
ax.errorbar(
np.array(range(8)),
school_effects_med,
yerr=[
school_effects_med - school_effects_low,
school_effects_hi - school_effects_med
],
fmt='none')
ax.legend(('avg_effect', 'HMC', 'Observed effect'), fontsize=14)
plt.xlabel('School')
plt.ylabel('Treatment effect')
plt.title('HMC estimated school treatment effects vs. observed data')
fig.set_size_inches(10, 8)
plt.show()
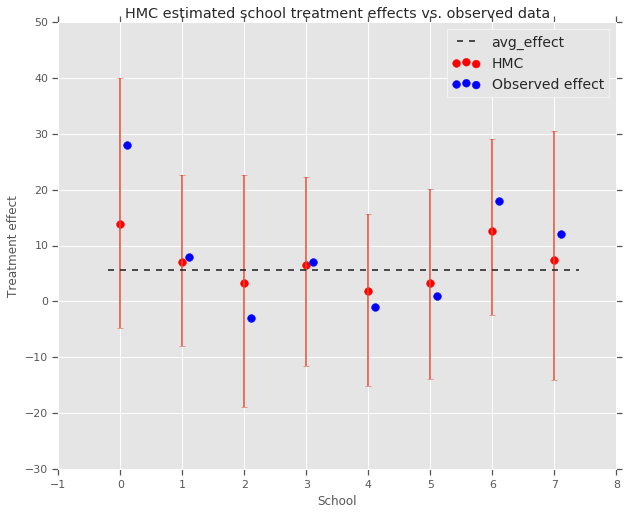
위의 avg_effect 그룹에 대한 축소를 관찰할 수 있습니다.
print("Inferred posterior mean: {0:.2f}".format(
np.mean(school_effects_samples[:,])))
print("Inferred posterior mean se: {0:.2f}".format(
np.std(school_effects_samples[:,])))
Inferred posterior mean: 6.97 Inferred posterior mean se: 10.41
비평
사후 예측 분포, 즉 관측된 데이터 \(y\)를 고려하여 새 데이터 \(y^*\)의 모델을 구합니다.
\[ p(y^*|y) \propto \int_\theta p(y^* | \theta)p(\theta |y)d\theta\]
모델의 확률 변수값을 재정의하여 사후 분포의 평균으로 설정하고, 해당 모델에서 샘플링하여 새 데이터 \(y^*\)를 생성합니다.
sample_shape = [5000]
_, _, _, predictive_treatment_effects = model.sample(
value=(tf.broadcast_to(np.mean(avg_effect, 0), sample_shape),
tf.broadcast_to(np.mean(avg_stddev, 0), sample_shape),
tf.broadcast_to(np.mean(school_effects_standard, 0),
sample_shape + [num_schools]),
None))
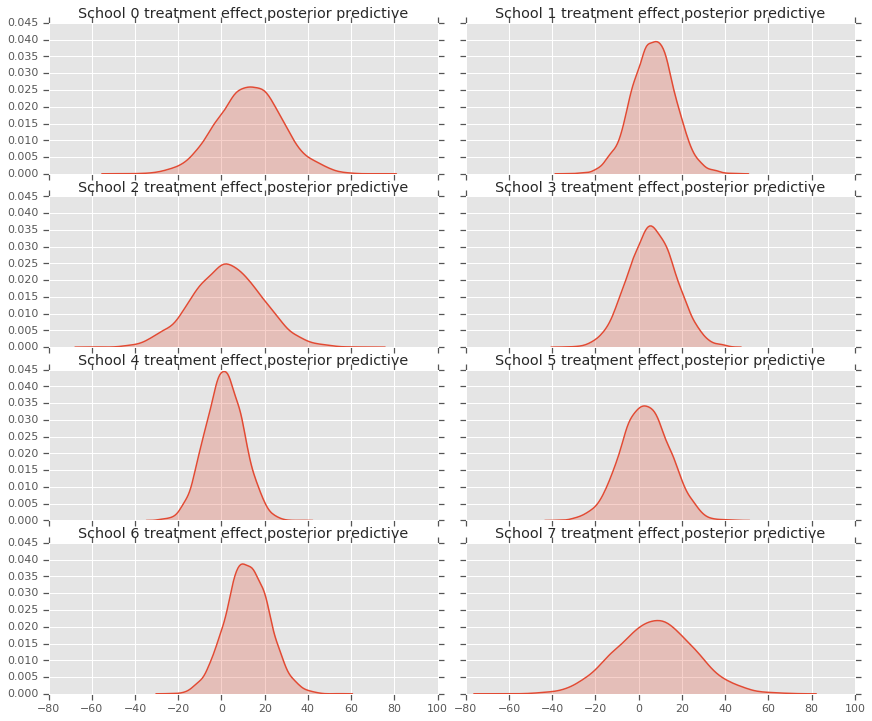
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(predictive_treatment_effects[:, 2*i].numpy(),
ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect posterior predictive".format(2*i))
sns.kdeplot(predictive_treatment_effects[:, 2*i + 1].numpy(),
ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect posterior predictive".format(2*i + 1))
plt.show()
# The mean predicted treatment effects for each of the eight schools.
prediction = np.mean(predictive_treatment_effects, axis=0)
처치 효과 데이터와 모델 사후 예측 간의 잔차를 볼 수 있습니다. 이는 모집단 평균에 대한 예상 효과의 축소를 보여주는 위의 플롯과 일치합니다.
treatment_effects - prediction
array([14.905351 , 1.2838383, -5.6966295, 0.8327627, -2.3356671,
-2.0363257, 5.997898 , 4.3731265], dtype=float32)
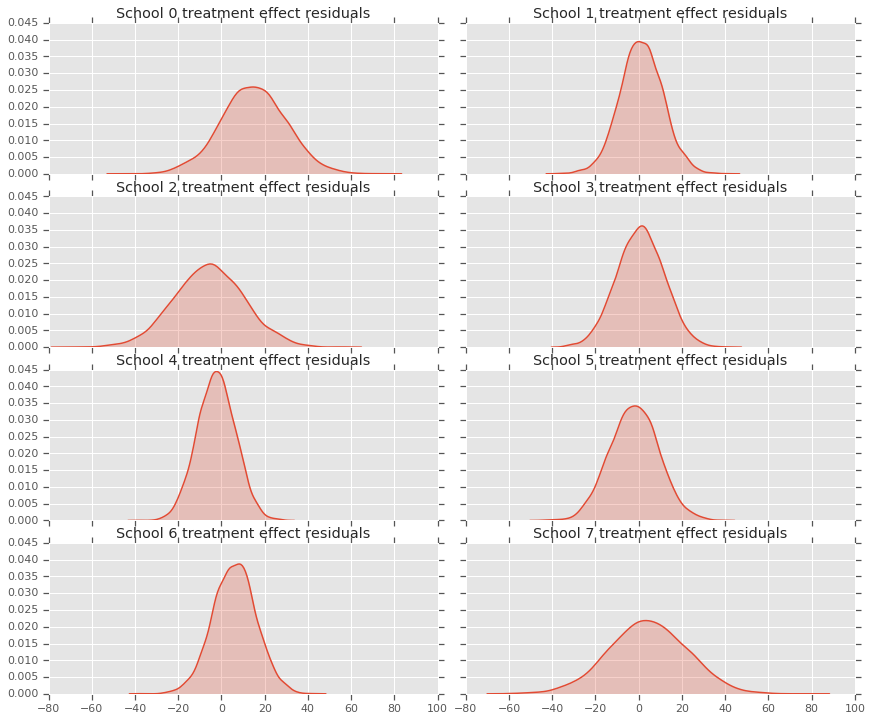
각 학교에 대한 예측 분포가 있으므로 잔차 분포도 고려할 수 있습니다.
residuals = treatment_effects - predictive_treatment_effects
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(residuals[:, 2*i].numpy(), ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect residuals".format(2*i))
sns.kdeplot(residuals[:, 2*i + 1].numpy(), ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect residuals".format(2*i + 1))
plt.show()
감사의 말
이 튜토리얼은 원래 Edward 1.0(소스)로 작성되었습니다. 해당 버전을 작성하고 수정하는데 기여해 주신 모든 분께 감사드립니다.
참고 문헌
- Donald B. Rubin. Estimation in parallel randomized experiments. Journal of Educational Statistics, 6(4):377-401, 1981.
- Andrew Gelman, John Carlin, Hal Stern, David Dunson, Aki Vehtari, and Donald Rubin. Bayesian Data Analysis, Third Edition. Chapman and Hall/CRC, 2013.
