वैरिएशनल इंट्रेंस का उपयोग करते हुए सामान्यीकृत रैखिक मिश्रित-प्रभाव वाले मॉडल की फिटिंग

TensorFlow.org पर देखें Google Colab में चलाएं GitHub पर स्रोत देखें नोटबुक डाउनलोड करें

इंस्टॉल

इंस्टॉल

सार

इस कोलाब में हम प्रदर्शित करते हैं कि TensorFlow प्रायिकता में परिवर्तनशील अनुमान का उपयोग करके एक सामान्यीकृत रैखिक मिश्रित-प्रभाव मॉडल को कैसे फिट किया जाए।

मॉडल परिवार

मिश्रित प्रभाव मॉडल रैखिक सामान्यीकृत (GLMM) के समान हैं रैखिक मॉडल सामान्यीकृत (GLM) सिवाय इसके कि वे भविष्यवाणी रैखिक प्रतिक्रिया में एक नमूना विशिष्ट शोर शामिल करते हैं। यह आंशिक रूप से उपयोगी है क्योंकि यह दुर्लभ रूप से देखी जाने वाली सुविधाओं को अधिक सामान्य रूप से देखी जाने वाली सुविधाओं के साथ जानकारी साझा करने की अनुमति देता है।

एक जनरेटिव प्रक्रिया के रूप में, एक सामान्यीकृत रैखिक मिश्रित-प्रभाव मॉडल (GLMM) की विशेषता है:

\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]

कहाँ पे:

\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]

दूसरे शब्दों में, यह कहा गया है कि प्रत्येक समूह के हर वर्ग एक नमूना है, साथ जुड़ा हुआ है \(\beta_{rc}\)बहुविविध सामान्य से,। हालांकि \(\beta_{rc}\) ड्रॉ हमेशा स्वतंत्र हैं, वे केवल indentically एक समूह के लिए वितरित कर रहे हैं \(r\): नोटिस है ठीक एक \(\Sigma_r\) प्रत्येक के लिए \(r\in\{1,\ldots,R\}\)।

Affinely एक नमूना के समूह के फ़ीचर (के साथ संयुक्त जब\(z_{r,i}\)), परिणाम पर नमूना-विशिष्ट शोर है \(i\)वें रैखिक प्रतिक्रिया की भविष्यवाणी की है (जो अन्यथा है \(x_i^\top\omega\))।

जब हम अनुमान \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) हम अनिवार्य रूप से शोर की मात्रा एक यादृच्छिक प्रभाव समूह में किया जाता है जो अन्यथा में संकेत मौजूद दबनी हैं का अनुमान लगा रहे \(x_i^\top\omega\)।

वहाँ के लिए विकल्प की एक किस्म है \(\text{Distribution}\) और उलटा लिंक समारोह , \(g^{-1}\)। आम विकल्प हैं:

  • \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
  • \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), और,
  • \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\)।

अधिक संभावनाएं के लिए, देखें tfp.glm मॉड्यूल।

भिन्नात्मक अनुमान

दुर्भाग्य से, पैरामीटर्स की अधिकतम संभावना अनुमान खोजने \(\beta,\{\Sigma_r\}_r^R\) जरूरत पर जोर देता एक गैर विश्लेषणात्मक अभिन्न। इस समस्या को दूर करने के लिए, हम इसके बजाय

  1. एक पैरामिट्रीकृत वितरण के परिवार ( "सरोगेट घनत्व"), निरूपित किया परिभाषित \(q_{\lambda}\) परिशिष्ट में।
  2. मापदंडों का पता लगाएं \(\lambda\) ताकि \(q_{\lambda}\) हमारे सच्चे लक्ष्य denstiy के करीब है।

वितरण के परिवार को उचित आयामों की स्वतंत्र Gaussians, और "हमारा लक्ष्य घनत्व के करीब" के द्वारा, हम मतलब है "कम से कम हो जाएगा Kullback-Leibler विचलन "। उदाहरण के लिए देखें, 'सांख्यिकीविदों के लिए एक समीक्षा परिवर्तन संबंधी निष्कर्ष "की धारा 2.2 एक अच्छी तरह से लिखा व्युत्पत्ति और प्रेरणा के लिए। विशेष रूप से, यह दर्शाता है कि केएल विचलन को कम करना नकारात्मक साक्ष्य को कम करने के बराबर है (ईएलबीओ)।

खिलौना समस्या

Gelman एट अल। के (2007) "राडोण डाटासेट" कभी कभी प्रतिगमन के लिए दृष्टिकोण प्रदर्शित करने के लिए प्रयोग किया जाता है एक डाटासेट है। (उदाहरण के लिए, इस बारीकी से संबंधित PyMC3 ब्लॉग पोस्ट ।) राडोण डाटासेट रेडॉन के इनडोर माप संयुक्त राज्य भर में ले लिया हैं। रेडॉन स्वाभाविक रूप से रेडियोधर्मी गैस जो है ocurring है विषाक्त उच्च सांद्रता में।

हमारे प्रदर्शन के लिए, मान लीजिए कि हम इस परिकल्पना को मान्य करने में रुचि रखते हैं कि बेसमेंट वाले घरों में रेडॉन का स्तर अधिक होता है। हमें यह भी संदेह है कि रेडॉन एकाग्रता मिट्टी के प्रकार, यानी भूगोल मामलों से संबंधित है।

इसे एक एमएल समस्या के रूप में फ्रेम करने के लिए, हम उस मंजिल के रैखिक कार्य के आधार पर लॉग-रेडॉन स्तरों की भविष्यवाणी करने का प्रयास करेंगे जिस पर रीडिंग ली गई थी। हम काउंटी को यादृच्छिक प्रभाव के रूप में भी उपयोग करेंगे और ऐसा करने में भूगोल के कारण भिन्नताओं के लिए खाते का उपयोग करेंगे। दूसरे शब्दों में, हम एक का उपयोग करेंगे सामान्यीकृत रैखिक मिश्रित प्रभाव मॉडल ।

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import os
from six.moves import urllib

import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

हम GPU की उपलब्धता की त्वरित जांच भी करेंगे:

if tf.test.gpu_device_name() != '/device:GPU:0':
  print("We'll just use the CPU for this run.")
else:
  print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))

We'll just use the CPU for this run.

डेटासेट प्राप्त करें:

हम TensorFlow डेटासेट से डेटासेट लोड करते हैं और कुछ हल्की प्रीप्रोसेसिंग करते हैं।

def load_and_preprocess_radon_dataset(state='MN'):
  """Load the Radon dataset from TensorFlow Datasets and preprocess it.

  Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
  to Minnesota data and preprocess to obtain the following features:
  - `county`: Name of county in which the measurement was taken.
  - `floor`: Floor of house (0 for basement, 1 for first floor) on which the
    measurement was taken.

  The target variable is `log_radon`, the log of the Radon measurement in the
  house.
  """
  ds = tfds.load('radon', split='train')
  radon_data = tfds.as_dataframe(ds)
  radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
  df = radon_data[radon_data.state==state.encode()].copy()

  df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
  # Make county names look nice. 
  df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
  # Remap categories to start from 0 and end at max(category).
  df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
  df['county_code'] = df.county.cat.codes
  # Radon levels are all positive, but log levels are unconstrained
  df['log_radon'] = df['radon'].apply(np.log)

  # Drop columns we won't use and tidy the index 
  columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
  df = df[columns_to_keep].reset_index(drop=True)

  return df

df = load_and_preprocess_radon_dataset()
df.head()

GLMM परिवार की विशेषज्ञता

इस खंड में, हम रेडॉन स्तरों की भविष्यवाणी करने के कार्य के लिए GLMM परिवार के विशेषज्ञ हैं। ऐसा करने के लिए, हम पहले GLMM के निश्चित-प्रभाव वाले विशेष मामले पर विचार करते हैं:

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]

यह मॉडल मानती है कि अवलोकन में लॉग राडोण \(j\) है (उम्मीद में) मंजिल द्वारा शासित \(j\)वें पढ़ने पर लिया जाता है, प्लस कुछ निरंतर अवरोधन। स्यूडोकोड में, हम लिख सकते हैं

def estimate_log_radon(floor):
    return intercept + floor_effect[floor]

वहाँ एक वजन हर मंजिल और एक सार्वभौमिक के लिए सीखा है intercept अवधि। मंजिल 0 और 1 से रेडॉन माप को देखते हुए, ऐसा लगता है कि यह एक अच्छी शुरुआत हो सकती है:

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')

df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");

पीएनजी

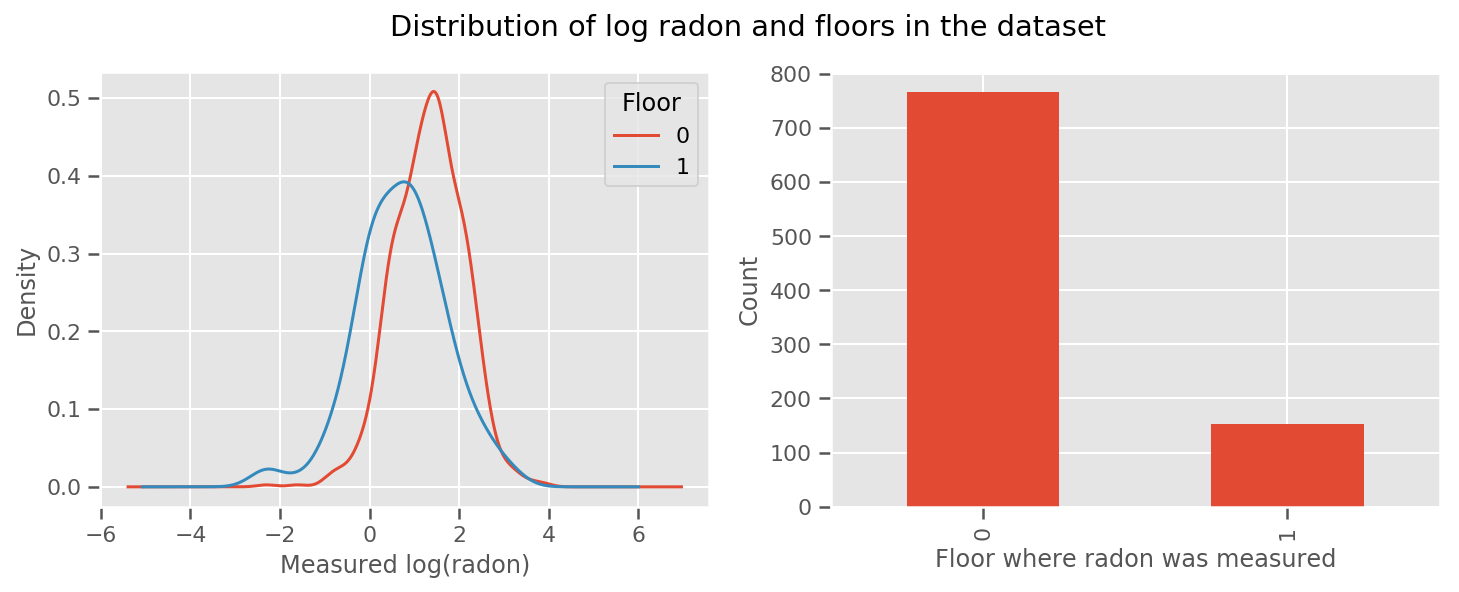
मॉडल को थोड़ा और परिष्कृत बनाने के लिए, भूगोल के बारे में कुछ सहित, शायद और भी बेहतर है: रेडॉन यूरेनियम की क्षय श्रृंखला का हिस्सा है, जो जमीन में मौजूद हो सकता है, इसलिए भूगोल को ध्यान में रखना महत्वपूर्ण लगता है।

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]

फिर से, स्यूडोकोड में, हमारे पास है

def estimate_log_radon(floor, county):
    return intercept + floor_effect[floor] + county_effect[county]

काउंटी-विशिष्ट वजन को छोड़कर पहले जैसा ही।

पर्याप्त रूप से बड़े प्रशिक्षण सेट को देखते हुए, यह एक उचित मॉडल है। हालाँकि, मिनेसोटा से हमारे डेटा को देखते हुए, हम देखते हैं कि वहाँ बड़ी संख्या में काउंटियाँ हैं जिनमें माप की एक छोटी संख्या है। उदाहरण के लिए, 85 में से 39 काउंटियों में पाँच से कम प्रेक्षण हैं।

यह हमारी सभी टिप्पणियों के बीच सांख्यिकीय ताकत को साझा करने के लिए प्रेरित करता है, इस तरह से उपरोक्त मॉडल में परिवर्तित हो जाता है क्योंकि प्रति काउंटी टिप्पणियों की संख्या बढ़ जाती है।

fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');

पीएनजी

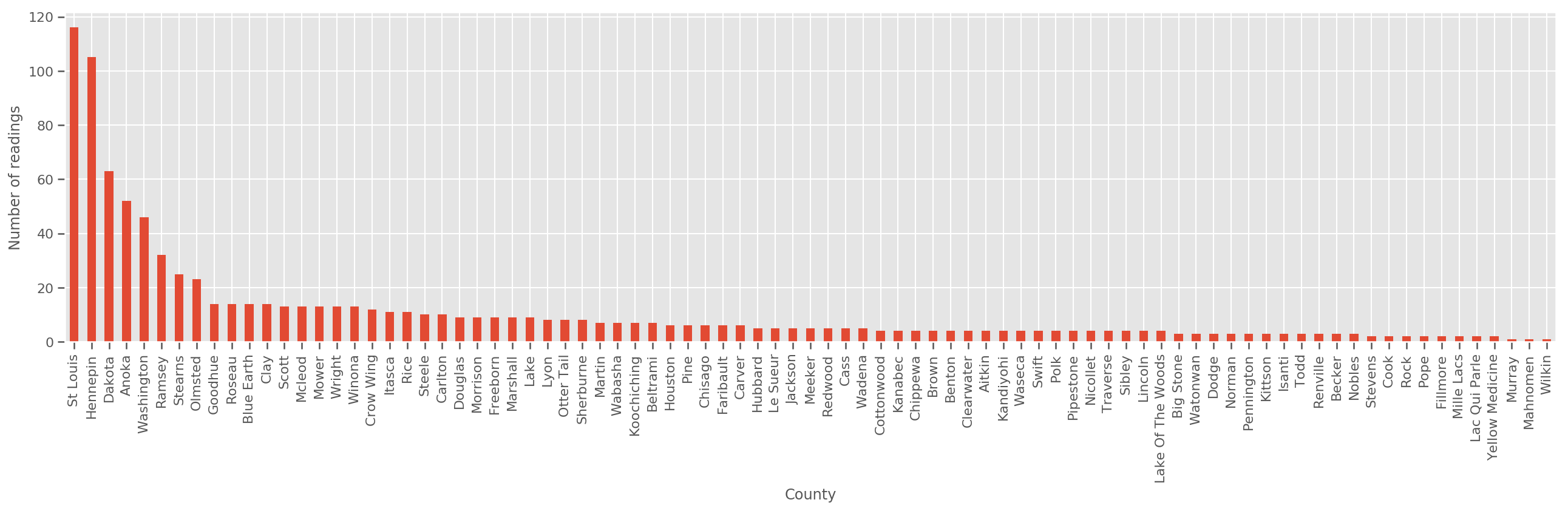
अगर हम इस मॉडल फिट, county_effect वेक्टर संभावना काउंटियों जो केवल कुछ प्रशिक्षण नमूने था, शायद overfitting और गरीब सामान्यीकरण करने के लिए अग्रणी के लिए परिणाम याद हो जाएंगे।

GLMM उपरोक्त दो GLM के लिए एक सुखद मध्य प्रदान करता है। हम फिटिंग पर विचार कर सकते हैं

\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]

यह मॉडल पहले के समान ही है, लेकिन हम अपने संभावना तय कर दी है एक सामान्य वितरण होने के लिए, और (एकल) चर के माध्यम से सभी काउंटियों में विचरण साझा करेंगे county_scale । स्यूडोकोड में,

def estimate_log_radon(floor, county):
    county_mean = county_effect[county]
    random_effect = np.random.normal() * county_scale + county_mean
    return intercept + floor_effect[floor] + random_effect

हम से अधिक संयुक्त वितरण का अनुमान लगा होगा county_scale , county_mean , और random_effect हमारे मनाया डेटा का उपयोग कर। वैश्विक county_scale कई टिप्पणियों के साथ उन कुछ टिप्पणियों के साथ काउंटियों में से भिन्न एक हिट प्रदान करते हैं: हमें काउंटियों में सांख्यिकीय ताकत साझा करने के लिए अनुमति देता है। इसके अलावा, जैसा कि हम अधिक डेटा इकट्ठा करते हैं, यह मॉडल पूल किए गए स्केल वैरिएबल के बिना मॉडल में परिवर्तित हो जाएगा - यहां तक ​​​​कि इस डेटासेट के साथ, हम किसी भी मॉडल के साथ सबसे अधिक देखे जाने वाले काउंटियों के बारे में समान निष्कर्ष पर आएंगे।

प्रयोग

अब हम TensorFlow में परिवर्तनशील अनुमान का उपयोग करके उपरोक्त GLMM को फिट करने का प्रयास करेंगे। पहले हम डेटा को सुविधाओं और लेबल में विभाजित करेंगे।

features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()

मॉडल निर्दिष्ट करें

def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):

  def model():
    county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
    intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
    floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
    county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
                                    scale=county_scale,
                                    name='county_prior')
    random_effect = tf.gather(county_prior, county, axis=-1)

    fixed_effect = intercept + floor_weight * floor
    linear_response = fixed_effect + random_effect
    yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
  return tfd.JointDistributionCoroutineAutoBatched(model)

joint = make_joint_distribution_coroutine(
    features.floor.values, features.county_code.values, df.county.nunique(),
    df.floor.nunique())

# Define a closure over the joint distribution 
# to condition on the observed labels.
def target_log_prob_fn(*args):
  return joint.log_prob(*args, likelihood=labels)

सरोगेट पोस्टीरियर निर्दिष्ट करें

अब हम एक साथ एक किराए परिवार डाल \(q_{\lambda}\), जहां मानकों \(\lambda\) trainable रहे हैं। इस मामले में, हमारे परिवार के स्वतंत्र मल्टीवेरिएट सामान्य वितरण, प्रत्येक पैरामीटर के लिए एक है, और है \(\lambda = \{(\mu_j, \sigma_j)\}\), जहां \(j\) अनुक्रमित चार मापदंडों।

विधि हम स्थानापन्न परिवार का उपयोग करता है फिट करने के लिए उपयोग करें tf.Variables । हम यह भी का उपयोग tfp.util.TransformedVariable के साथ Softplus (trainable) पैमाने मापदंडों विवश करने के लिए सकारात्मक हो सकता है। इसके अतिरिक्त, हम लागू Softplus पूरे करने के लिए scale_prior है, जो एक सकारात्मक पैरामीटर है।

अनुकूलन में सहायता के लिए हम इन प्रशिक्षित चरों को थोड़ा घबराहट के साथ प्रारंभ करते हैं।

# Initialize locations and scales randomly with `tf.Variable`s and 
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
    tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
    initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
    bijector=tfb.Softplus())
n_counties = df.county.nunique()

surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
  tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())),           # scale_prior
  tfd.Normal(_init_loc(), _init_scale()),                           # intercept
  tfd.Normal(_init_loc(), _init_scale()),                           # floor_weight
  tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))])  # county_prior

नोट इस सेल के साथ बदला जा सकता है कि tfp.experimental.vi.build_factored_surrogate_posterior के रूप में,:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
  event_shape=joint.event_shape_tensor()[:-1],
  constraining_bijectors=[tfb.Softplus(), None, None, None])

परिणाम

याद रखें कि हमारा लक्ष्य वितरण के एक ट्रैक्टेबल पैरामीटरयुक्त परिवार को परिभाषित करना है, और फिर पैरामीटर का चयन करना है ताकि हमारे पास एक ट्रैक्टेबल वितरण हो जो हमारे लक्ष्य वितरण के करीब हो।

हम ऊपर सरोगेट वितरण का निर्माण किया है, और उपयोग कर सकते हैं tfp.vi.fit_surrogate_posterior है, जो एक अनुकूलक और कदम की दी गई संख्या को स्वीकार करता है सरोगेट मॉडल नकारात्मक ELBO कम करने के लिए मानकों (जो बीच Kullback-Liebler विचलन को कम करने के लिए corresonds को खोजने के लिए सरोगेट और लक्ष्य वितरण)।

वापसी मान प्रत्येक चरण में नकारात्मक ELBO है, और में वितरण surrogate_posterior मानकों के साथ अनुकूलक को अपडेट हो जाएंगे।

optimizer = tf.optimizers.Adam(learning_rate=1e-2)

losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn, 
    surrogate_posterior,
    optimizer=optimizer,
    num_steps=3000, 
    seed=42,
    sample_size=2)

(scale_prior_, 
 intercept_, 
 floor_weight_, 
 county_weights_), _ = surrogate_posterior.sample_distributions()

print('        intercept (mean): ', intercept_.mean())
print('     floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))

intercept (mean):  tf.Tensor(1.4352839, shape=(), dtype=float32)
     floor_weight (mean):  tf.Tensor(-0.6701997, shape=(), dtype=float32)
 scale_prior (approx. mean):  tf.Tensor(0.28682157, shape=(), dtype=float32)

fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
       ylabel="Loss (ELBO)",
       title="Loss during training",
       ylim=0);

पीएनजी

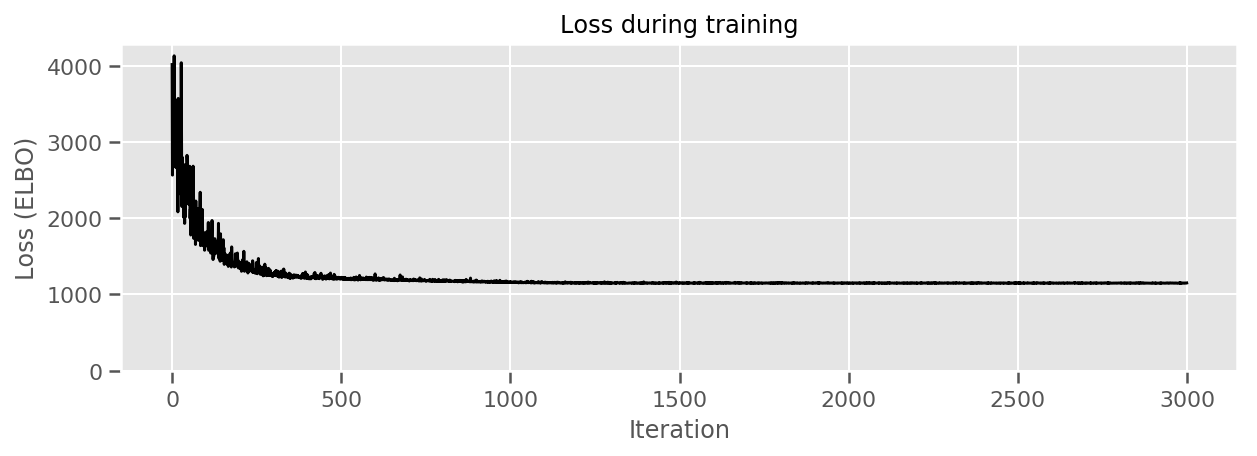
हम उस माध्य की अनिश्चितता के साथ-साथ अनुमानित माध्य काउंटी प्रभावों की साजिश रच सकते हैं। हमने इसे प्रेक्षणों की संख्या के आधार पर आदेश दिया है, जिसमें सबसे बड़ा बाईं ओर है। ध्यान दें कि कई टिप्पणियों वाले काउंटियों के लिए अनिश्चितता छोटी है, लेकिन उन काउंटियों के लिए बड़ी है जिनमें केवल एक या दो अवलोकन हैं।

county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
                   .agg('size')
                   .sort_values(ascending=False)
                   .reset_index(name='count'))

means = county_weights_.mean()
stds = county_weights_.stddev()

fig, ax = plt.subplots(figsize=(20, 5))

for idx, row in county_counts.iterrows():
  mid = means[row.county_code]
  std = stds[row.county_code]
  ax.vlines(idx, mid - std, mid + std, linewidth=3)
  ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)

ax.set(
    xticks=np.arange(len(county_counts)),
    xlim=(-1, len(county_counts)),
    ylabel="County effect",
    title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);

पीएनजी

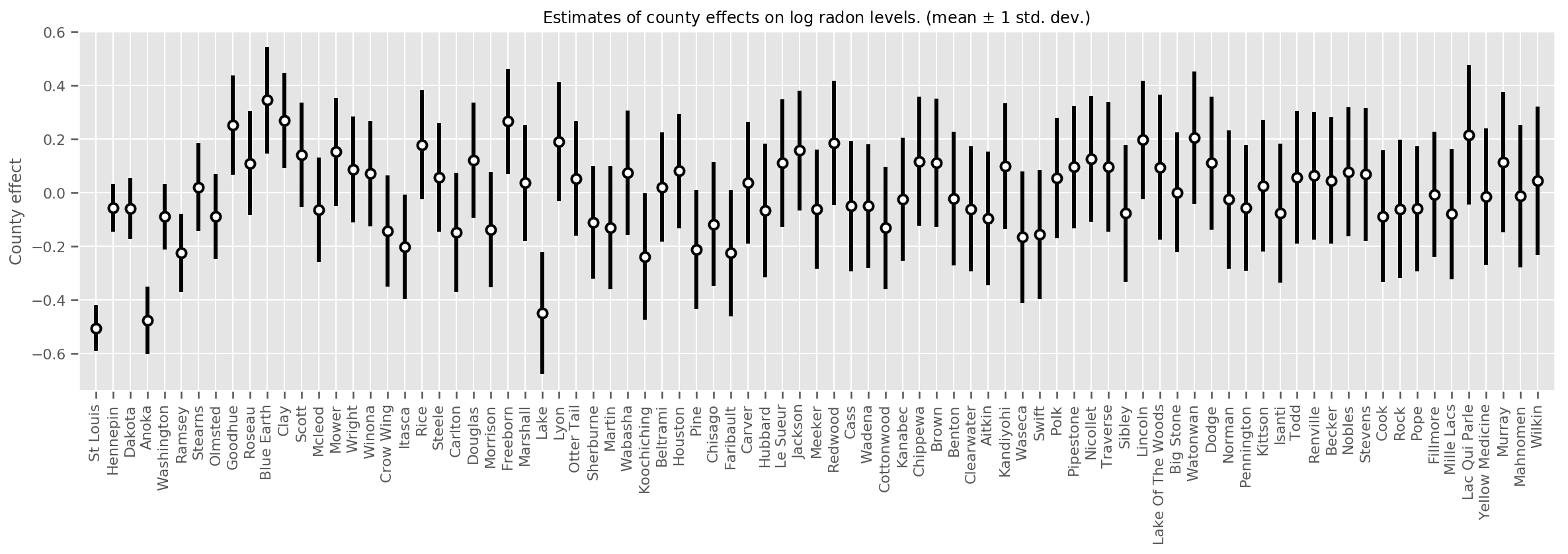
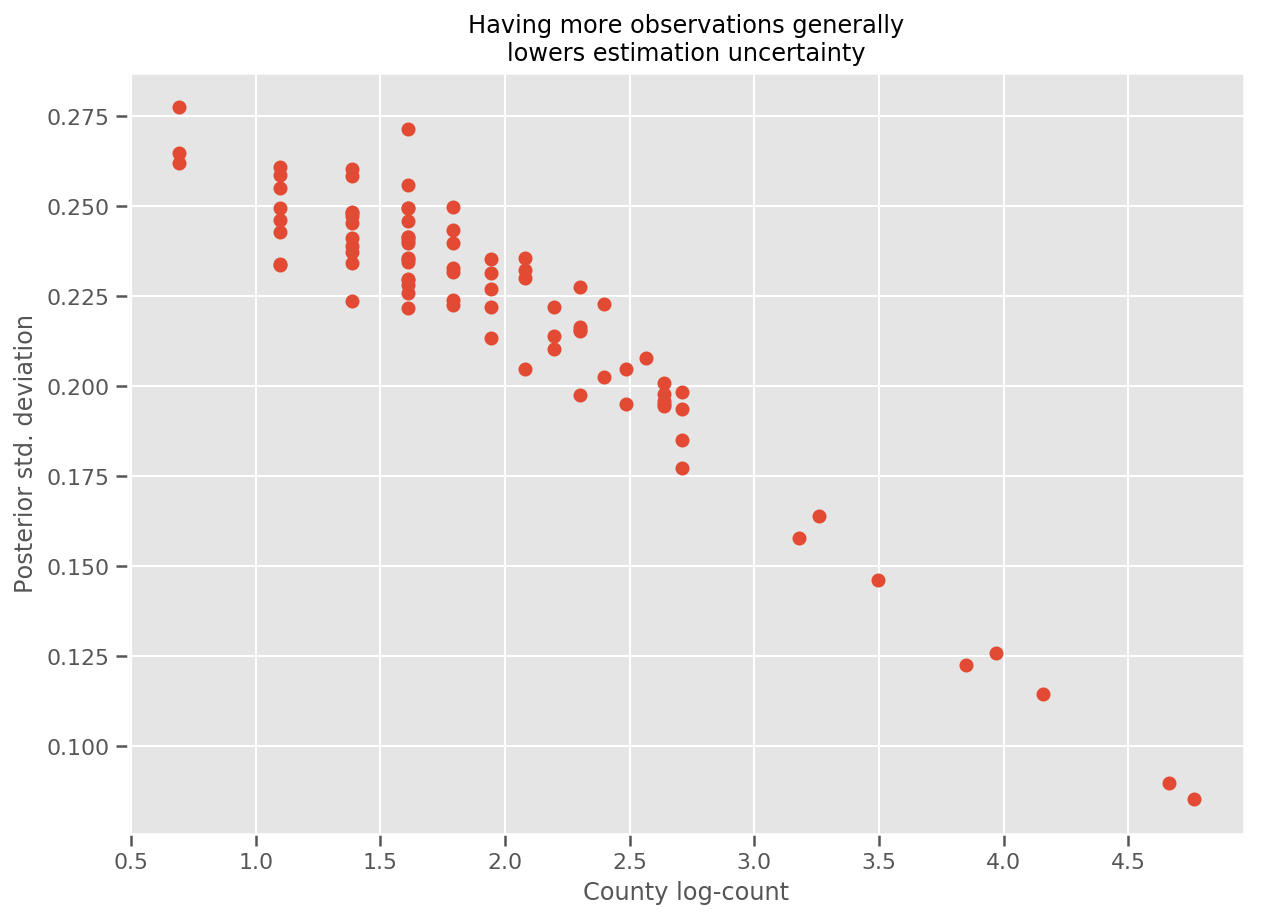
वास्तव में, हम अनुमानित मानक विचलन के खिलाफ टिप्पणियों की लॉग-संख्या की साजिश रचकर इसे और अधिक सीधे देख सकते हैं, और देख सकते हैं कि संबंध लगभग रैखिक है।

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
    ylabel='Posterior std. deviation',
    xlabel='County log-count',
    title='Having more observations generally\nlowers estimation uncertainty'
);

पीएनजी

इसकी तुलना में lme4 आर में

%%shell
exit  # Trick to make this block not execute.

radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)

# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit

# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
#    Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
#  Groups   Name        Std.Dev.
#  county   (Intercept) 0.3282
#  Residual             0.7556
# Number of obs: 919, groups:  county, 85
# Fixed Effects:
# (Intercept)        floor
#       1.462       -0.693

<IPython.core.display.Javascript at 0x7f90b888e9b0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90bce1dfd0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>

निम्न तालिका परिणामों को सारांशित करती है।

print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
                             floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
                             scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
                   index=['lme4', 'vi']))

intercept   floor     scale
lme4   1.462000 -0.6930  0.328200
vi     1.435284 -0.6702  0.287251

इस तालिका में इंगित करता है छठी परिणाम ~ भीतर कर रहे हैं के 10% lme4 की। यह कुछ आश्चर्यजनक है क्योंकि:

  • lme4 पर आधारित है लाप्लास की विधि (नहीं VI),
  • इस कोलाब में वास्तव में अभिसरण करने का कोई प्रयास नहीं किया गया था,
  • हाइपरपैरामीटर को ट्यून करने के लिए न्यूनतम प्रयास किया गया था,
  • डेटा को नियमित या प्रीप्रोसेस करने के लिए कोई प्रयास नहीं किया गया था (उदाहरण के लिए, केंद्र की विशेषताएं, आदि)।

निष्कर्ष

इस कोलाब में हमने सामान्यीकृत रैखिक मिश्रित-प्रभाव मॉडल का वर्णन किया और दिखाया कि टेंसरफ्लो प्रोबेबिलिटी का उपयोग करके उन्हें फिट करने के लिए विभिन्न अनुमानों का उपयोग कैसे करें। हालाँकि खिलौने की समस्या में केवल कुछ सौ प्रशिक्षण नमूने थे, यहाँ उपयोग की जाने वाली तकनीकें उसी के समान हैं जिसकी बड़े पैमाने पर आवश्यकता है।