 TensorFlow.org에서 보기 TensorFlow.org에서 보기 |  Google Colab에서 실행 Google Colab에서 실행 |  GitHub에서 소스 보기 GitHub에서 소스 보기 |  노트북 다운로드 노트북 다운로드 |
선형 혼합 효과 모델은 구조화된 선형 관계를 모델링하기 위한 간단한 접근 방식입니다(Harville, 1997; Laird and Ware, 1982). 각 데이터 포인트는 그룹으로 분류된 다양한 유형의 입력과 실제 값 출력으로 구성됩니다. 선형 혼합 효과 모델 계층 모델이다 : 그것은 개별 데이터 포인트에 대한 추정을 향상시키기 위해 그룹간에 통계적 강도를 공유한다.
이 튜토리얼에서는 TensorFlow Probability의 실제 예제를 사용하여 선형 혼합 효과 모델을 보여줍니다. 우리는 JointDistributionCoroutine과 마르코프 체인 몬테 카를로 (사용합니다 tfp.mcmc ) 모듈을.
종속성 및 전제 조건
가져오기 및 설정
import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')
일을 빨리 만드십시오!
본격적으로 시작하기 전에 이 데모에 GPU를 사용하고 있는지 확인하겠습니다.
이렇게 하려면 "런타임" -> "런타임 유형 변경" -> "하드웨어 가속기" -> "GPU"를 선택합니다.
다음 스니펫은 GPU에 대한 액세스 권한이 있는지 확인합니다.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
데이터
우리는 사용 InstEval 인기에서 데이터 세트 lme4 R의 패키지 (베이츠 등을., 2015). 코스와 평가 등급의 데이터 세트입니다. 각 코스는 다음과 같은 메타 데이터를 포함하고 students , instructors , 및 departments , 관심있는 반응 변수는 평가 등급이다.
def load_insteval():
"""Loads the InstEval data set.
It contains 73,421 university lecture evaluations by students at ETH
Zurich with a total of 2,972 students, 2,160 professors and
lecturers, and several student, lecture, and lecturer attributes.
Implementation is built from the `observations` Python package.
Returns:
Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
dictionary `metadata` of column headers (feature names).
"""
url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
'lme4/InstEval.csv')
with requests.Session() as s:
download = s.get(url)
f = download.content.decode().splitlines()
iterator = csv.reader(f)
columns = next(iterator)[1:]
x_train = np.array([row[1:] for row in iterator], dtype=np.int)
metadata = {'columns': columns}
return x_train, metadata
데이터 세트를 로드하고 사전 처리합니다. 우리는 보이지 않는 데이터 포인트에 대한 피팅 모델을 평가할 수 있도록 데이터의 20%를 보유합니다. 아래에서 처음 몇 행을 시각화합니다.
data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
'd': 'instructors',
'dept': 'departments',
'y': 'ratings'})
data['students'] -= 1 # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes
train = data.sample(frac=0.8)
test = data.drop(train.index)
train.head()
우리는 측면에서 데이터 세트를 설정 features 입력의 사전을하고 labels 출력은 등급에 해당. 각 기능은 정수로 인코딩되고 각 레이블(평가 등급)은 부동 소수점 숫자로 인코딩됩니다.
get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
k: get_value(train, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)
features_test = {k: get_value(test, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)
num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]
print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)
Number of students: 2972 Number of instructors: 1128 Number of departments: 14 Number of observations: 58737
모델
일반적인 선형 모델은 데이터 포인트 쌍이 일정한 선형 관계를 갖는 독립성을 가정합니다. 에서 InstEval 데이터 세트 관찰 다양한 슬로프와 차단이있을 수 있습니다 각각의 그룹에서 발생한다. 계층적 선형 모델 또는 다단계 선형 모델이라고도 하는 선형 혼합 효과 모델은 이러한 현상을 포착합니다(Gelman & Hill, 2006).
이 현상의 예는 다음과 같습니다.
- 학생들. 학생의 관찰은 독립적이지 않습니다. 일부 학생은 체계적으로 낮은(또는 높은) 강의 평점을 줄 수 있습니다.
- 강사. 강사의 관찰은 독립적이지 않습니다. 좋은 교사는 일반적으로 좋은 평가를 받고 나쁜 교사는 일반적으로 나쁜 평가를 받을 것으로 기대합니다.
- 부서. 부서의 관찰은 독립적이지 않습니다. 특정 부서는 일반적으로 건조 자료 또는 더 엄격한 등급을 가지고 있으므로 다른 부서보다 낮은 평가를 받을 수 있습니다.
이, 데이터 세트에 대한 리콜 캡처하려면 \(N\times D\) 기능 \(\mathbf{X}\) 및 \(N\) 라벨 \(\mathbf{y}\)모델, 선형 회귀 단정을
\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]
기울기 벡터가이고 \(\beta\in\mathbb{R}^D\), 인터셉트 \(\alpha\in\mathbb{R}\), 랜덤 잡음 \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). 우리는 그 말을 \(\beta\) 및 \(\alpha\) "고정 효과"이다 : 그들은 데이터 포인트의 인구에 걸쳐 일정하게 유지 효과가 있습니다 \((x, y)\). 우도와 같은 식의 등가 제제는 \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\). 이 가능성은 점 추정 찾기 위해 추론 과정을 극대화 \(\beta\) 및 \(\alpha\) 데이터를 맞습니다.
선형 혼합 효과 모델은 선형 회귀를 다음과 같이 확장합니다.
\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]
여전히 기울기 벡터가있는 곳에 \(\beta\in\mathbb{R}^P\), 절편 \(\alpha\in\mathbb{R}\), 랜덤 노이즈 \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). 또한, 용어가 \(\mathbf{Z}\eta\), \(\mathbf{Z}\) 특징의 행렬이고 \(\eta\in\mathbb{R}^Q\) 임의의 경사 벡터된다; \(\eta\) 정상적으로 분산 요소 파라미터와 함께 배포되는 \(\sigma^2\). \(\mathbf{Z}\) 동일한 분할에 의해 형성된다 \(N\times D\) 새로운 관점에서 매트릭스 기능 \(N\times P\) 매트릭스 \(\mathbf{X}\) 및 \(N\times Q\) 매트릭스 \(\mathbf{Z}\), \(P + Q=D\)이 파티션은 우리가 사용하는 별개의 기능을 모델링 할 수 : 고정 효과 \(\beta\) 및 잠재 변수 \(\eta\) 각각.
우리는 잠재 변수 말 \(\eta\) "임의 효과"이다 : 그들은 (그들이 부분 집단에서 일정을 수 있지만) 인구에 걸쳐 변화 효과입니다. 임의 효과가 있기 때문에 특히, \(\eta\) 데이터 라벨의 평균에 의해 캡처, 평균 0을 \(\mathbf{X}\beta + \alpha\). 임의의 효과 성분 \(\mathbf{Z}\eta\) 데이터 캡쳐를 변화 ". (54)은 높은 평균 1.4 점을 평가한다 # 강사"예를 들면,
이 자습서에서는 다음 효과를 가정합니다.
- 고정 효과 :
service.service과정 강사의 주요 부서에 속하는지 여부에 해당하는 바이너리 공변량이다. 우리가 수집 얼마나 많은 추가 데이터에 상관없이, 그것은 단지 값을 취할 수 \(0\) 및 \(1\). - 랜덤 효과 :
students,instructors및departments. 과정 평가 등급의 모집단에서 더 많은 관찰이 주어지면 새로운 학생, 교사 또는 부서를 볼 수 있습니다.
R의 lme4 패키지 구문(Bates et al., 2015)에서 모델은 다음과 같이 요약될 수 있습니다.
ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1
여기서 x 는 고정 효과를 나타낸다 (1|x) 대한 임의의 효과를 나타내고, x 및 1 절편 용어이다.
아래에서 이 모델을 JointDistribution으로 구현합니다. 매개 변수 추적을위한 더 나은 지원하도록하려면 (예를 우리는 모두 추적 할 tf.Variable 에 model.trainable_variables , 우리가 모델 템플릿 구현) tf.Module .
class LinearMixedEffectModel(tf.Module):
def __init__(self):
# Set up fixed effects and other parameters.
# These are free parameters to be optimized in E-steps
self._intercept = tf.Variable(0., name="intercept") # alpha in eq
self._effect_service = tf.Variable(0., name="effect_service") # beta in eq
self._stddev_students = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_students") # sigma in eq
self._stddev_instructors = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_instructors") # sigma in eq
self._stddev_departments = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_departments") # sigma in eq
def __call__(self, features):
model = tfd.JointDistributionSequential([
# Set up random effects.
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_students),
scale_identity_multiplier=self._stddev_students),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_instructors),
scale_identity_multiplier=self._stddev_instructors),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_departments),
scale_identity_multiplier=self._stddev_departments),
# This is the likelihood for the observed.
lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
tfd.Normal(
loc=(self._effect_service * features["service"] +
tf.gather(effect_students, features["students"], axis=-1) +
tf.gather(effect_instructors, features["instructors"], axis=-1) +
tf.gather(effect_departments, features["departments"], axis=-1) +
self._intercept),
scale=1.),
reinterpreted_batch_ndims=1)
])
# To enable tracking of the trainable variables via the created distribution,
# we attach a reference to `self`. Since all TFP objects sub-class
# `tf.Module`, this means that the following is possible:
# LinearMixedEffectModel()(features_train).trainable_variables
# ==> tuple of all tf.Variables created by LinearMixedEffectModel.
model._to_track = self
return model
lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)
lmm_train.trainable_variables
(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)
확률적 그래픽 프로그램으로서 우리는 계산 그래프의 관점에서 모델의 구조를 시각화할 수도 있습니다. 이 그래프는 프로그램의 무작위 변수에 걸친 데이터 흐름을 인코딩하여 그래픽 모델 측면에서 그들의 관계를 명시적으로 만듭니다(Jordan, 2003).
통계 도구로서, 우리는, 예를 들어, 더 나은보기 위해 그래프에서 그 보일 수 있습니다 intercept 하고 effect_service 조건에 따라 주어진 ratings ; 프로그램이 클래스, 모듈 간 상호 참조 및/또는 서브루틴으로 작성된 경우 소스 코드에서 보기가 더 어려울 수 있습니다. 전산 도구로서, 우리는 또한 잠재 변수가 유입 알 수 있습니다 ratings 을 통해 변수 tf.gather 작전. 색인 경우 특정 하드웨어 가속기에 병목 현상이있을 수 있습니다 Tensor 의 비싼; 그래프를 시각화하면 이를 쉽게 알 수 있습니다.
lmm_train.resolve_graph()
(('effect_students', ()),
('effect_instructors', ()),
('effect_departments', ()),
('x', ('effect_departments', 'effect_instructors', 'effect_students')))
매개변수 추정
데이터를 감안할 때, 추론의 목표는 모델의 고정 효과 경사에 맞게하는 것입니다 \(\beta\), 절편 \(\alpha\)및 분산 구성 요소 매개 변수 \(\sigma^2\). 최대 가능성 원칙은 이 작업을 다음과 같이 공식화합니다.
\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]
이 튜토리얼에서 우리는 이 한계 밀도를 최대화하기 위해 Monte Carlo EM 알고리즘을 사용합니다(Dempster et al., 1977; Wei and Tanner, 1990).¹ 우리는 Markov chain Monte Carlo를 수행하여 무작위 효과("E-step"), 그리고 매개변수("M-step")에 대한 기대치를 최대화하기 위해 기울기 하강을 수행합니다.
E-step의 경우 Hamiltonian Monte Carlo(HMC)를 설정했습니다. 현재 상태(학생, 강사 및 부서 효과)를 가져와서 새 상태를 반환합니다. HMC 체인의 상태를 나타내는 TensorFlow 변수에 새 상태를 할당합니다.
M 단계의 경우 HMC의 사후 샘플을 사용하여 최대 상수까지 한계 가능성의 편향되지 않은 추정치를 계산합니다. 그런 다음 관심 매개변수에 대한 기울기를 적용합니다. 이것은 한계 가능성에 대한 편견 없는 확률적 하강 단계를 생성합니다. Adam TensorFlow 옵티마이저로 구현하고 한계의 음수를 최소화합니다.
target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]
# For debugging
target_log_prob_fn(*current_state)
<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>
# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.015,
num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)
@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
next_state, next_kernel_results = hmc.one_step(
current_state=current_state,
previous_kernel_results=kernel_results)
return next_state, next_kernel_results
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
with tf.GradientTape() as tape:
loss = -target_log_prob_fn(*current_state)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
우리는 훈련이 사후 확률 질량 내에서 초기화될 수 있도록 여러 반복 동안 하나의 MCMC 체인을 실행하는 워밍업 단계를 수행합니다. 그런 다음 훈련 루프를 실행합니다. E 및 M 단계를 공동으로 실행하고 훈련 중에 값을 기록합니다.
num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])
# Run warm-up stage.
for t in range(num_warmup_iters):
current_state, kernel_results = one_e_step(current_state, kernel_results)
num_accepted += kernel_results.is_accepted.numpy()
if t % 500 == 0 or t == num_warmup_iters - 1:
print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
t, num_accepted / (t + 1)))
num_accepted = 0 # reset acceptance rate counter
# Run training.
for t in range(num_iters):
# run 5 MCMC iterations before every joint EM update
for _ in range(5):
current_state, kernel_results = one_e_step(current_state, kernel_results)
loss = one_m_step(current_state)
effect_students_samples[t, :] = current_state[0].numpy()
effect_instructors_samples[t, :] = current_state[1].numpy()
effect_departments_samples[t, :] = current_state[2].numpy()
num_accepted += kernel_results.is_accepted.numpy()
loss_history[t] = loss.numpy()
if t % 500 == 0 or t == num_iters - 1:
print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
t, num_accepted / (t + 1), loss_history[t]))
Warm-Up Iteration: 0 Acceptance Rate: 1.000 Warm-Up Iteration: 500 Acceptance Rate: 0.754 Warm-Up Iteration: 999 Acceptance Rate: 0.707 Iteration: 0 Acceptance Rate: 1.000 Loss: 98220.266 Iteration: 500 Acceptance Rate: 0.703 Loss: 96003.969 Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609 Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891
당신은 또한에 대한 루프 예열 쓸 수 tf.while_loop , 그리고에 훈련 단계 tf.scan 하거나 tf.while_loop 더 빠른 추론을 위해. 예를 들어:
@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
_, next_state, next_kernel_results = tf.while_loop(
cond=lambda i, state, pkr: i < k,
body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
loop_vars=(tf.constant(0), current_state, kernel_results)
)
return next_state, next_kernel_results
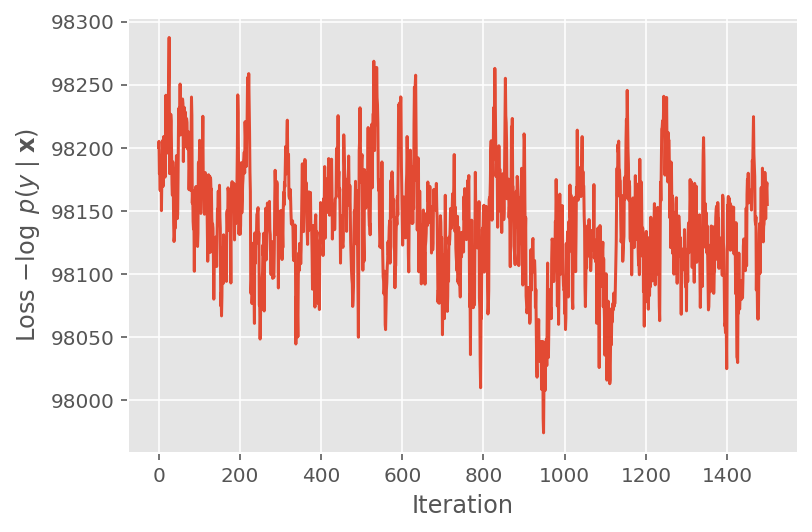
위에서 우리는 수렴 임계값이 감지될 때까지 알고리즘을 실행하지 않았습니다. 훈련이 합리적인지 확인하기 위해 손실 함수가 훈련 반복에 걸쳐 실제로 수렴하는 경향이 있는지 확인합니다.
plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()
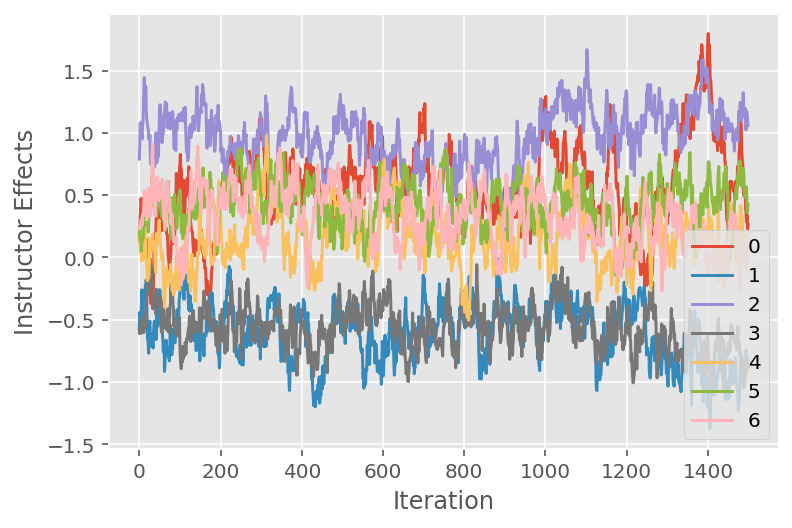
우리는 또한 특정 잠재 차원에 걸쳐 Markov chain Monte Carlo 알고리즘의 궤적을 보여주는 추적 플롯을 사용합니다. 아래에서 특정 강사 효과가 초기 상태에서 실제로 의미 있게 전환되고 상태 공간을 탐색하는 것을 볼 수 있습니다. 추적 플롯은 또한 효과가 강사에 따라 다르지만 혼합 동작은 유사함을 나타냅니다.
for i in range(7):
plt.plot(effect_instructors_samples[:, i])
plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()
비판
위에서 우리는 모델을 맞추었습니다. 이제 모델을 탐색하고 더 잘 이해할 수 있는 데이터를 사용하여 적합성을 비판하는 방법을 살펴봅니다. 이러한 기술 중 하나는 각 데이터 포인트에 대한 모델의 예측과 정답 간의 차이를 표시하는 잔차 플롯입니다. 모델이 정확하다면 그 차이는 표준 정규 분포를 따라야 합니다. 플롯에서 이 패턴의 모든 편차는 모델 부적합을 나타냅니다.
우선 순위에 대한 사후 예측 분포를 형성하여 잔차 플롯을 작성합니다. 이는 무작위 효과에 대한 사전 분포를 사후 주어진 훈련 데이터로 대체합니다. 특히, 우리는 모델을 앞으로 실행하고 추론된 사후 평균을 사용하여 사전 무작위 효과에 대한 종속성을 가로챕니다.²
lmm_test = lmm_jointdist(features_test)
[
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
] = [
np.mean(x, axis=0).astype(np.float32) for x in [
effect_students_samples,
effect_instructors_samples,
effect_departments_samples
]
]
# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
value=(
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
))
ratings_prediction = ratings_posterior.mean()
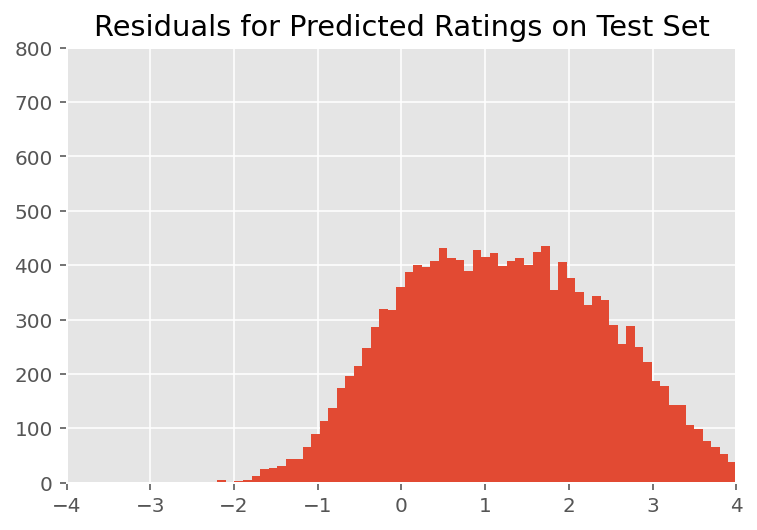
육안 검사에서 잔차는 다소 표준 정규 분포를 보입니다. 그러나 적합은 완벽하지 않습니다. 꼬리에 정규 분포보다 확률 질량이 더 크며, 이는 모델이 정규성 가정을 완화하여 적합도를 향상시킬 수 있음을 나타냅니다.
가에서 모델 등급에 정규 분포를 사용하는 것이 가장 일반적이지만 특히, InstEval 데이터 세트를, 데이터에 면밀한 관찰은 물론 평가 등급이 우리가 사용되어야 함을 시사 1에서 5로 사실 순서 값에 밝혀 순서 분포, 또는 상대 순서를 버릴 만큼 충분한 데이터가 있는 경우 범주형입니다. 이것은 위의 모델에 대한 한 줄 변경입니다. 동일한 추론 코드가 적용됩니다.
plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()
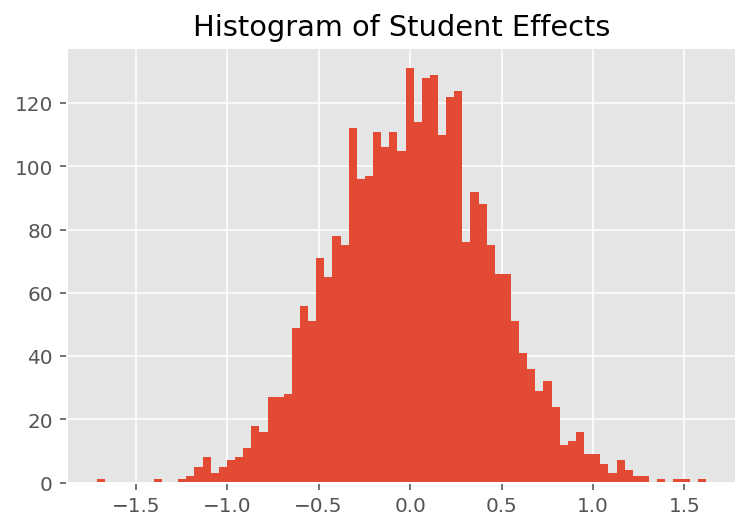
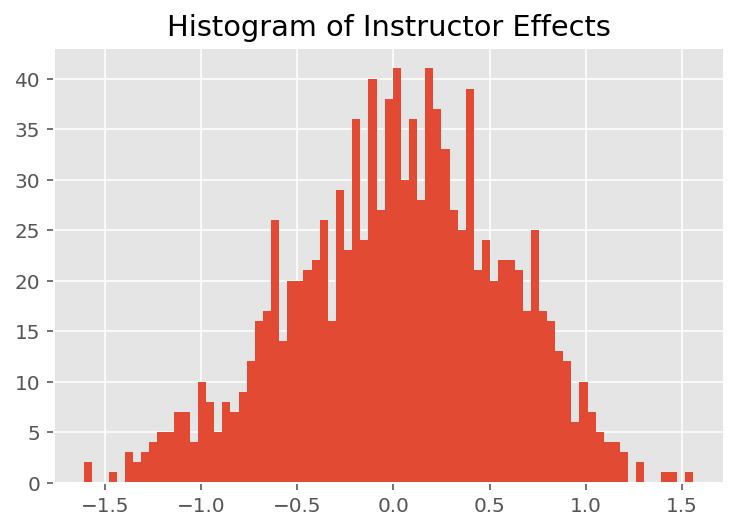
모델이 개별 예측을 수행하는 방법을 탐색하기 위해 학생, 강사 및 부서에 대한 효과의 히스토그램을 살펴봅니다. 이를 통해 데이터 포인트의 특징 벡터에 있는 개별 요소가 결과에 어떻게 영향을 미치는지 이해할 수 있습니다.
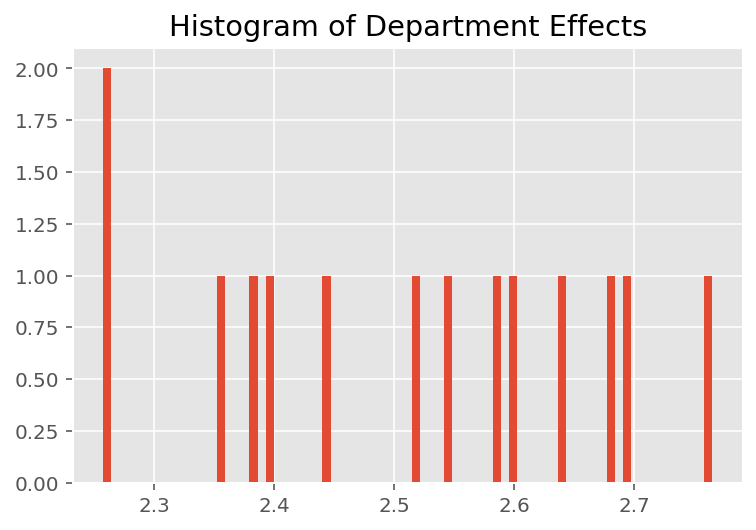
당연히 아래에서 각 학생이 강사의 평가 등급에 거의 영향을 미치지 않는다는 것을 알 수 있습니다. 흥미롭게도 우리는 강사가 속한 학과의 영향력이 크다는 것을 알 수 있습니다.
plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()
plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()
plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()
각주
¹ 선형 혼합 효과 모델은 한계 밀도를 분석적으로 계산할 수 있는 특별한 경우입니다. 이 자습서의 목적을 위해 확률이 정규 대신 범주형으로 확장된 경우와 같이 비분석적 한계 밀도에 더 쉽게 적용되는 Monte Carlo EM을 시연합니다.
² 단순화를 위해 모델의 단 하나의 전진 패스를 사용하여 예측 분포의 평균을 형성합니다. 이것은 사후 평균에 대한 조건화에 의해 수행되며 선형 혼합 효과 모델에 유효합니다. 그러나 이것은 일반적으로 유효하지 않습니다. 사후 예측 분포의 평균은 일반적으로 다루기 어려우며 주어진 사후 샘플이 제공된 모델의 여러 전진 패스에 걸쳐 경험적 평균을 취해야 합니다.
감사의 말
이 튜토리얼은 원래 에드워드 1.0 (로 작성된 소스 ). 해당 버전을 작성하고 수정한 모든 기여자에게 감사드립니다.
참고문헌
Douglas Bates와 Martin Machler, Ben Bolker, Steve Walker. lme4를 사용한 선형 혼합 효과 모델 피팅. 통계 소프트웨어, 67의 전표 (1) : 1-48, 2015.
Arthur P. Dempster, Nan M. Laird, Donald B. Rubin. EM 알고리즘을 통한 불완전한 데이터의 최대 가능성. 왕립 통계 학회 논문집, 시리즈 B (방법론), 1-38, 1977.
앤드류 겔만과 제니퍼 힐. 회귀 및 다단계/계층적 모델을 사용한 데이터 분석. 캠브리지 대학 출판부, 2006.
데이비드 A. 하빌. 분산 성분 추정 및 관련 문제에 대한 최대 가능성 접근 방식. 미국의 통계 학회지, 72 (358) : 320-338, 1977.
마이클 I. 조던. 그래픽 모델 소개. 기술 보고서, 2003.
Nan M. Laird와 James Ware. 종단 데이터에 대한 랜덤 효과 모델. 생체 인식, 963-974, 1982.
그렉 웨이와 마틴 A. 태너. EM 알고리즘과 가난한 사람의 데이터 증대 알고리즘의 몬테카를로 구현. 미국 통계 학회 논문집, 699-704, 1990.
