이 예는 PyMC3 예 노트북에서 이식 다단계 모델링을위한 베이지안 방법에 뇌관
 TensorFlow.org에서 보기 TensorFlow.org에서 보기 |  Google Colab에서 실행 Google Colab에서 실행 |  GitHub에서 소스 보기 GitHub에서 소스 보기 |  노트북 다운로드 노트북 다운로드 |
종속성 및 전제 조건
수입
import collections
import os
from six.moves import urllib
import daft as daft
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import warnings
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
tfk = tf.keras
tfkl = tf.keras.layers
tfpl = tfp.layers
tfd = tfp.distributions
tfb = tfp.bijectors
warnings.simplefilter('ignore')
1. 소개
이 colab에서 우리는 인기있는 라돈 데이터 세트를 사용하여 계층 적 선형 모델 모델의 복잡성의 다양한 정도의 (HLMs)를 맞습니다. 우리는 TFP 프리미티브와 Markov Chain Monte Carlo 도구 세트를 사용할 것입니다.
데이터를 더 잘 맞추기 위해 우리의 목표는 데이터 세트에 있는 자연스러운 계층 구조를 사용하는 것입니다. 우리는 완전히 풀링된 모델과 풀링되지 않은 모델인 기존 접근 방식으로 시작합니다. 우리는 부분 풀링 모델, 그룹 수준 예측 변수 및 컨텍스트 효과를 탐색하는 다단계 모델을 계속 사용합니다.
관련 노트북과 같은 조사, 라돈 데이터 세트를 사용하여 TFP HLMs 피팅 {TF 확률 R 스탠} 선형 혼합 효과 회귀 .
여기 자료에 대해 궁금한 점이 있으면 연락 주시기 (또는 가입)하지 않는 TensorFlow 확률 메일 링리스트 . 기꺼이 도와드리겠습니다.
2 다단계 모델링 개요
다단계 모델링을 위한 베이지안 방법에 대한 입문서
계층적 또는 다단계 모델링은 회귀 모델링의 일반화입니다.
다단계 모델은 구성 모델 매개변수에 확률 분포가 제공되는 회귀 모델입니다. 이는 모델 매개변수가 그룹별로 다를 수 있음을 의미합니다. 관측 단위는 종종 자연스럽게 클러스터됩니다. 클러스터링은 클러스터의 무작위 샘플링과 클러스터 내 무작위 샘플링에도 불구하고 관찰 간에 종속성을 유도합니다.
계층적 모델은 매개변수가 서로 중첩되는 특정 다단계 모델입니다. 일부 다단계 구조는 계층적이지 않습니다.
예를 들어 "국가"와 "연도"는 중첩되지 않지만 개별적이지만 중첩되는 매개변수 클러스터를 나타낼 수 있습니다. 환경 역학 예를 사용하여 이 주제에 동기를 부여할 것입니다.
예: 라돈 오염(Gelman and Hill 2006)
라돈은 지면과의 접촉점을 통해 가정으로 유입되는 방사성 가스입니다. 비흡연자에서 폐암의 주요 원인이 되는 발암물질입니다. 라돈 수치는 가정마다 크게 다릅니다.
EPA는 80,000가구에서 라돈 수준에 대한 연구를 수행했습니다. 두 가지 중요한 예측 변수는 다음과 같습니다. 1. 지하 또는 1층에서의 측정(지하실에서 더 높은 라돈) 2. 카운티 우라늄 수준(라돈 수준과 양의 상관 관계)
우리는 미네소타의 라돈 수준 모델링에 집중할 것입니다. 이 예에서 계층 구조는 각 카운티 내의 가구입니다.
3 데이터 통합
이 섹션에서 우리는 얻을 radon 데이터 세트 와 최소한의 전처리을한다.
def load_and_preprocess_radon_dataset(state='MN'):
"""Preprocess Radon dataset as done in "Bayesian Data Analysis" book.
We filter to Minnesota data (919 examples) and preprocess to obtain the
following features:
- `log_uranium_ppm`: Log of soil uranium measurements.
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
# For any missing or invalid activity readings, we'll use a value of `0.1`.
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
county_name = sorted(df.county.unique())
df['county'] = df.county.astype(
pd.api.types.CategoricalDtype(categories=county_name)).cat.codes
county_name = list(map(str.strip, county_name))
df['log_radon'] = df['radon'].apply(np.log)
df['log_uranium_ppm'] = df['Uppm'].apply(np.log)
df = df[['idnum', 'log_radon', 'floor', 'county', 'log_uranium_ppm']]
return df, county_name
radon, county_name = load_and_preprocess_radon_dataset()
num_counties = len(county_name)
num_observations = len(radon)
# Create copies of variables as Tensors.
county = tf.convert_to_tensor(radon['county'], dtype=tf.int32)
floor = tf.convert_to_tensor(radon['floor'], dtype=tf.float32)
log_radon = tf.convert_to_tensor(radon['log_radon'], dtype=tf.float32)
log_uranium = tf.convert_to_tensor(radon['log_uranium_ppm'], dtype=tf.float32)
radon.head()
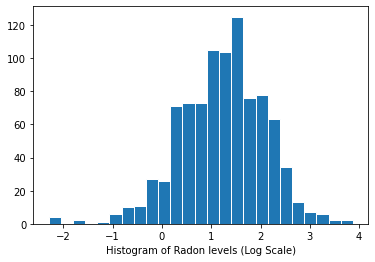
라돈 수준 분포(로그 척도):
plt.hist(log_radon.numpy(), bins=25, edgecolor='white')
plt.xlabel("Histogram of Radon levels (Log Scale)")
plt.show()
4 기존 접근 방식
라돈 노출 모델링에 대한 두 가지 기존 대안은 편향-분산 트레이드오프의 두 극단을 나타냅니다.
완전한 풀링:
모든 카운티를 동일하게 취급하고 단일 라돈 수준을 추정합니다.
\[y_i = \alpha + \beta x_i + \epsilon_i\]
풀링 없음:
각 카운티의 라돈을 독립적으로 모델링합니다.
\(y_i = \alpha_{j[i]} + \beta x_i + \epsilon_i\) 곳 \(j = 1,\ldots,85\)
오류의 \(\epsilon_i\) 주택 중 측정 오류, 시간 내에서 자체의 변화, 또는 변화를 나타낼 수있다.
4.1 완전한 풀링 모델
pgm = daft.PGM([7, 3.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"alpha_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
3,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"beta_prior",
r"$\mathcal{N}(0, 10^5)$",
2.5,
3,
fixed=True,
offset=(10, 5)))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4.5,
3,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("alpha", r"$\alpha$", 1, 2))
pgm.add_node(daft.Node("beta", r"$\beta$", 2.5, 2))
pgm.add_node(daft.Node("sigma", r"$\sigma$", 4.5, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 3, 1, scale=1.25, observed=True))
pgm.add_edge("alpha_prior", "alpha")
pgm.add_edge("beta_prior", "beta")
pgm.add_edge("sigma_prior", "sigma")
pgm.add_edge("sigma", "y_i")
pgm.add_edge("alpha", "y_i")
pgm.add_edge("beta", "y_i")
pgm.add_plate(daft.Plate([2.3, 0.1, 1.4, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
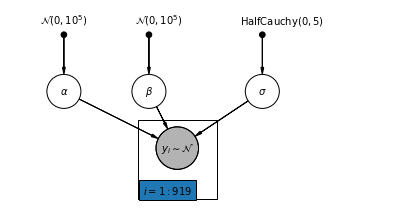
아래에서 우리는 Hamiltonian Monte Carlo를 사용하여 완전한 풀링 모델을 피팅합니다.
@tf.function
def affine(x, kernel_diag, bias=tf.zeros([])):
"""`kernel_diag * x + bias` with broadcasting."""
kernel_diag = tf.ones_like(x) * kernel_diag
bias = tf.ones_like(x) * bias
return x * kernel_diag + bias
def pooled_model(floor):
"""Creates a joint distribution representing our generative process."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # alpha
tfd.Normal(loc=0., scale=1e5), # beta
tfd.HalfCauchy(loc=0., scale=5), # sigma
lambda s, b1, b0: tfd.MultivariateNormalDiag( # y
loc=affine(floor, b1[..., tf.newaxis], b0[..., tf.newaxis]),
scale_identity_multiplier=s)
])
@tf.function
def pooled_log_prob(alpha, beta, sigma):
"""Computes `joint_log_prob` pinned at `log_radon`."""
return pooled_model(floor).log_prob([alpha, beta, sigma, log_radon])
@tf.function
def sample_pooled(num_chains, num_results, num_burnin_steps, num_observations):
"""Samples from the pooled model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=pooled_log_prob,
num_leapfrog_steps=10,
step_size=0.005)
initial_state = [
tf.zeros([num_chains], name='init_alpha'),
tf.zeros([num_chains], name='init_beta'),
tf.ones([num_chains], name='init_sigma')
]
# Constrain `sigma` to the positive real axis. Other variables are
# unconstrained.
unconstraining_bijectors = [
tfb.Identity(), # alpha
tfb.Identity(), # beta
tfb.Exp() # sigma
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
PooledModel = collections.namedtuple('PooledModel', ['alpha', 'beta', 'sigma'])
samples, acceptance_probs = sample_pooled(
num_chains=4,
num_results=1000,
num_burnin_steps=1000,
num_observations=num_observations)
print('Acceptance Probabilities for each chain: ', acceptance_probs.numpy())
pooled_samples = PooledModel._make(samples)
Acceptance Probabilities for each chain: [0.997 0.99 0.997 0.995]
for var, var_samples in pooled_samples._asdict().items():
print('R-hat for ', var, ':\t',
tfp.mcmc.potential_scale_reduction(var_samples).numpy())
R-hat for alpha : 1.0046891 R-hat for beta : 1.0128309 R-hat for sigma : 1.0010641
def reduce_samples(var_samples, reduce_fn):
"""Reduces across leading two dims using reduce_fn."""
# Collapse the first two dimensions, typically (num_chains, num_samples), and
# compute np.mean or np.std along the remaining axis.
if isinstance(var_samples, tf.Tensor):
var_samples = var_samples.numpy() # convert to numpy array
var_samples = np.reshape(var_samples, (-1,) + var_samples.shape[2:])
return np.apply_along_axis(reduce_fn, axis=0, arr=var_samples)
sample_mean = lambda samples : reduce_samples(samples, np.mean)
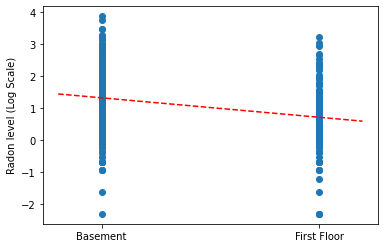
완전한 풀링 모델에 대한 기울기와 절편의 점 추정치를 플로팅합니다.
LinearEstimates = collections.namedtuple('LinearEstimates',
['intercept', 'slope'])
pooled_estimate = LinearEstimates(
intercept=sample_mean(pooled_samples.alpha),
slope=sample_mean(pooled_samples.beta)
)
plt.scatter(radon.floor, radon.log_radon)
xvals = np.linspace(-0.2, 1.2)
plt.ylabel('Radon level (Log Scale)')
plt.xticks([0, 1], ['Basement', 'First Floor'])
plt.plot(xvals, pooled_estimate.intercept + pooled_estimate.slope * xvals, 'r--')
plt.show()
샘플링된 변수의 추적을 플롯하는 유틸리티 함수입니다.
def plot_traces(var_name, samples, num_chains):
if isinstance(samples, tf.Tensor):
samples = samples.numpy() # convert to numpy array
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
axes[0].plot(samples[:, chain], alpha=0.7)
axes[0].title.set_text("'{}' trace".format(var_name))
sns.kdeplot(samples[:, chain], ax=axes[1], shade=False)
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
axes[1].set_xlabel(var_name)
plt.show()
for var, var_samples in pooled_samples._asdict().items():
plot_traces(var, samples=var_samples, num_chains=4)



다음으로 풀링되지 않은 모델에서 각 카운티의 라돈 수준을 추정합니다.
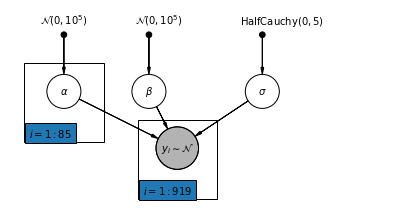
4.2 풀링되지 않은 모델
pgm = daft.PGM([7, 3.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"alpha_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
3,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"beta_prior",
r"$\mathcal{N}(0, 10^5)$",
2.5,
3,
fixed=True,
offset=(10, 5)))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4.5,
3,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("alpha", r"$\alpha$", 1, 2))
pgm.add_node(daft.Node("beta", r"$\beta$", 2.5, 2))
pgm.add_node(daft.Node("sigma", r"$\sigma$", 4.5, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 3, 1, scale=1.25, observed=True))
pgm.add_edge("alpha_prior", "alpha")
pgm.add_edge("beta_prior", "beta")
pgm.add_edge("sigma_prior", "sigma")
pgm.add_edge("sigma", "y_i")
pgm.add_edge("alpha", "y_i")
pgm.add_edge("beta", "y_i")
pgm.add_plate(daft.Plate([0.3, 1.1, 1.4, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([2.3, 0.1, 1.4, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
def unpooled_model(floor, county):
"""Creates a joint distribution for the unpooled model."""
return tfd.JointDistributionSequential([
tfd.MultivariateNormalDiag( # alpha
loc=tf.zeros([num_counties]), scale_identity_multiplier=1e5),
tfd.Normal(loc=0., scale=1e5), # beta
tfd.HalfCauchy(loc=0., scale=5), # sigma
lambda s, b1, b0: tfd.MultivariateNormalDiag( # y
loc=affine(
floor, b1[..., tf.newaxis], tf.gather(b0, county, axis=-1)),
scale_identity_multiplier=s)
])
@tf.function
def unpooled_log_prob(beta0, beta1, sigma):
"""Computes `joint_log_prob` pinned at `log_radon`."""
return (
unpooled_model(floor, county).log_prob([beta0, beta1, sigma, log_radon]))
@tf.function
def sample_unpooled(num_chains, num_results, num_burnin_steps):
"""Samples from the unpooled model."""
# Initialize the HMC transition kernel.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unpooled_log_prob,
num_leapfrog_steps=10,
step_size=0.025)
initial_state = [
tf.zeros([num_chains, num_counties], name='init_beta0'),
tf.zeros([num_chains], name='init_beta1'),
tf.ones([num_chains], name='init_sigma')
]
# Contrain `sigma` to the positive real axis. Other variables are
# unconstrained.
unconstraining_bijectors = [
tfb.Identity(), # alpha
tfb.Identity(), # beta
tfb.Exp() # sigma
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
UnpooledModel = collections.namedtuple('UnpooledModel',
['alpha', 'beta', 'sigma'])
samples, acceptance_probs = sample_unpooled(
num_chains=4, num_results=1000, num_burnin_steps=1000)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
unpooled_samples = UnpooledModel._make(samples)
print('R-hat for beta:',
tfp.mcmc.potential_scale_reduction(unpooled_samples.beta).numpy())
print('R-hat for sigma:',
tfp.mcmc.potential_scale_reduction(unpooled_samples.sigma).numpy())
Acceptance Probabilities: [0.892 0.897 0.911 0.91 ] R-hat for beta: 1.0079623 R-hat for sigma: 1.0059084
plot_traces(var_name='beta', samples=unpooled_samples.beta, num_chains=4)
plot_traces(var_name='sigma', samples=unpooled_samples.sigma, num_chains=4)


다음은 각 체인에 대한 95% 신뢰 구간과 함께 절편에 대한 풀링되지 않은 카운티 예상 값입니다. 또한 각 카운티의 추정치에 대한 R-hat 값을 보고합니다.
Forest 플롯에 대한 유틸리티 함수입니다.
def forest_plot(num_chains, num_vars, var_name, var_labels, samples):
fig, axes = plt.subplots(
1, 2, figsize=(12, 15), sharey=True, gridspec_kw={'width_ratios': [3, 1]})
for var_idx in range(num_vars):
values = samples[..., var_idx]
rhat = tfp.mcmc.diagnostic.potential_scale_reduction(values).numpy()
meds = np.median(values, axis=-2)
los = np.percentile(values, 5, axis=-2)
his = np.percentile(values, 95, axis=-2)
for i in range(num_chains):
height = 0.1 + 0.3 * var_idx + 0.05 * i
axes[0].plot([los[i], his[i]], [height, height], 'C0-', lw=2, alpha=0.5)
axes[0].plot([meds[i]], [height], 'C0o', ms=1.5)
axes[1].plot([rhat], [height], 'C0o', ms=4)
axes[0].set_yticks(np.linspace(0.2, 0.3, num_vars))
axes[0].set_ylim(0, 26)
axes[0].grid(which='both')
axes[0].invert_yaxis()
axes[0].set_yticklabels(var_labels)
axes[0].xaxis.set_label_position('top')
axes[0].set(xlabel='95% Credible Intervals for {}'.format(var_name))
axes[1].set_xticks([1, 2])
axes[1].set_xlim(0.95, 2.05)
axes[1].grid(which='both')
axes[1].set(xlabel='R-hat')
axes[1].xaxis.set_label_position('top')
plt.show()
forest_plot(
num_chains=4,
num_vars=num_counties,
var_name='alpha',
var_labels=county_name,
samples=unpooled_samples.alpha.numpy())

라돈 수치가 높은 카운티를 식별하기 위해 정렬된 추정치를 그릴 수 있습니다.
unpooled_intercepts = reduce_samples(unpooled_samples.alpha, np.mean)
unpooled_intercepts_se = reduce_samples(unpooled_samples.alpha, np.std)
def plot_ordered_estimates():
means = pd.Series(unpooled_intercepts, index=county_name)
std_errors = pd.Series(unpooled_intercepts_se, index=county_name)
order = means.sort_values().index
plt.plot(range(num_counties), means[order], '.')
for i, m, se in zip(range(num_counties), means[order], std_errors[order]):
plt.plot([i, i], [m - se, m + se], 'C0-')
plt.xlabel('Ordered county')
plt.ylabel('Radon estimate')
plt.show()
plot_ordered_estimates()
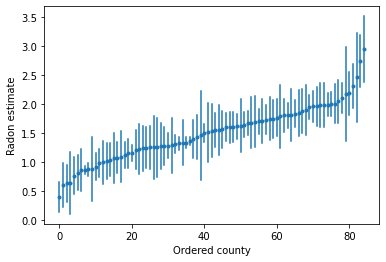
카운티 샘플 세트에 대한 추정치를 표시하는 유틸리티 함수입니다.
def plot_estimates(linear_estimates, labels, sample_counties):
fig, axes = plt.subplots(2, 4, figsize=(12, 6), sharey=True, sharex=True)
axes = axes.ravel()
intercepts_indexed = []
slopes_indexed = []
for intercepts, slopes in linear_estimates:
intercepts_indexed.append(pd.Series(intercepts, index=county_name))
slopes_indexed.append(pd.Series(slopes, index=county_name))
markers = ['-', 'r--', 'k:']
sample_county_codes = [county_name.index(c) for c in sample_counties]
for i, c in enumerate(sample_county_codes):
y = radon.log_radon[radon.county == c]
x = radon.floor[radon.county == c]
axes[i].scatter(
x + np.random.randn(len(x)) * 0.01, y, alpha=0.4, label='Log Radon')
# Plot both models and data
xvals = np.linspace(-0.2, 1.2)
for k in range(len(intercepts_indexed)):
axes[i].plot(
xvals,
intercepts_indexed[k][c] + slopes_indexed[k][c] * xvals,
markers[k],
label=labels[k])
axes[i].set_xticks([0, 1])
axes[i].set_xticklabels(['Basement', 'First Floor'])
axes[i].set_ylim(-1, 3)
axes[i].set_title(sample_counties[i])
if not i % 2:
axes[i].set_ylabel('Log Radon level')
axes[3].legend(bbox_to_anchor=(1.05, 0.9), borderaxespad=0.)
plt.show()
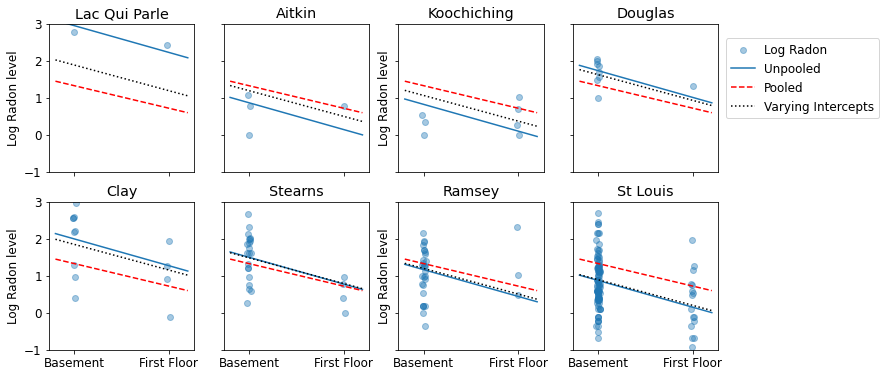
다음은 다양한 표본 크기를 나타내는 카운티의 하위 집합에 대한 합동 추정치와 합동 처리되지 않은 추정치를 시각적으로 비교한 것입니다.
unpooled_estimates = LinearEstimates(
sample_mean(unpooled_samples.alpha),
sample_mean(unpooled_samples.beta)
)
sample_counties = ('Lac Qui Parle', 'Aitkin', 'Koochiching', 'Douglas', 'Clay',
'Stearns', 'Ramsey', 'St Louis')
plot_estimates(
linear_estimates=[unpooled_estimates, pooled_estimate],
labels=['Unpooled Estimates', 'Pooled Estimates'],
sample_counties=sample_counties)
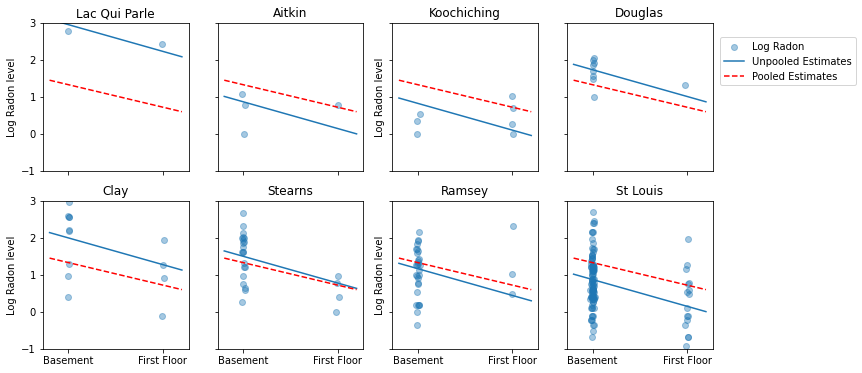
다음 모델 중 어느 것도 만족스럽지 않습니다.
- 고 라돈 카운티를 식별하려는 경우 풀링은 유용하지 않습니다.
- 우리는 소수의 관측치를 사용하는 모델에 의해 생성된 극단적인 풀링되지 않은 추정치를 신뢰하지 않습니다.
5 다단계 및 계층 모델
데이터를 풀링할 때 다른 데이터 포인트가 다른 카운티에서 왔다는 정보를 잃게 됩니다. 각 수단이 있다는 radon - 레벨 관측이 동일한 확률 분포로부터 샘플링된다. 이러한 모델은 그룹(예: 카운티) 내에 고유한 샘플링 단위의 변형을 학습하지 못합니다. 샘플링 분산만 설명합니다.
mpl.rc("font", size=18)
pgm = daft.PGM([13.6, 2.2], origin=[1.15, 1.0], node_ec="none")
pgm.add_node(daft.Node("parameter", r"parameter", 2.0, 3))
pgm.add_node(daft.Node("observations", r"observations", 2.0, 2))
pgm.add_node(daft.Node("theta", r"$\theta$", 5.5, 3))
pgm.add_node(daft.Node("y_0", r"$y_0$", 4, 2))
pgm.add_node(daft.Node("y_1", r"$y_1$", 5, 2))
pgm.add_node(daft.Node("dots", r"$\cdots$", 6, 2))
pgm.add_node(daft.Node("y_k", r"$y_k$", 7, 2))
pgm.add_edge("theta", "y_0")
pgm.add_edge("theta", "y_1")
pgm.add_edge("theta", "y_k")
pgm.render()
plt.show()
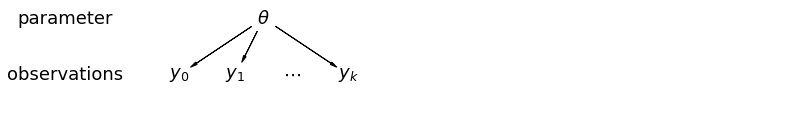
풀링되지 않은 데이터를 분석할 때 별도의 모델과 독립적으로 샘플링됨을 의미합니다. 풀링된 경우의 반대 극단에서 이 접근 방식은 샘플링 단위 간의 차이가 너무 커서 결합할 수 없다고 주장합니다.
mpl.rc("font", size=18)
pgm = daft.PGM([13.6, 2.2], origin=[1.15, 1.0], node_ec="none")
pgm.add_node(daft.Node("parameter", r"parameter", 2.0, 3))
pgm.add_node(daft.Node("observations", r"observations", 2.0, 2))
pgm.add_node(daft.Node("theta_0", r"$\theta_0$", 4, 3))
pgm.add_node(daft.Node("theta_1", r"$\theta_1$", 5, 3))
pgm.add_node(daft.Node("theta_dots", r"$\cdots$", 6, 3))
pgm.add_node(daft.Node("theta_k", r"$\theta_k$", 7, 3))
pgm.add_node(daft.Node("y_0", r"$y_0$", 4, 2))
pgm.add_node(daft.Node("y_1", r"$y_1$", 5, 2))
pgm.add_node(daft.Node("y_dots", r"$\cdots$", 6, 2))
pgm.add_node(daft.Node("y_k", r"$y_k$", 7, 2))
pgm.add_edge("theta_0", "y_0")
pgm.add_edge("theta_1", "y_1")
pgm.add_edge("theta_k", "y_k")
pgm.render()
plt.show()
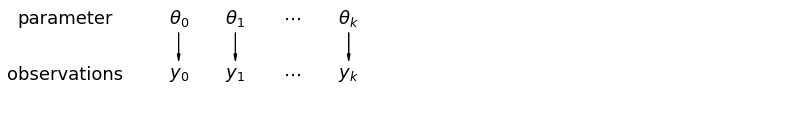
계층적 모델에서 모수는 모수 모집단 분포의 표본으로 간주됩니다. 따라서 우리는 그것들을 완전히 다르거나 완전히 동일하지 않은 것으로 봅니다. 이것은 부분적 풀링으로 알려져있다.
mpl.rc("font", size=18)
pgm = daft.PGM([13.6, 3.4], origin=[1.15, 1.0], node_ec="none")
pgm.add_node(daft.Node("model", r"model", 2.0, 4))
pgm.add_node(daft.Node("parameter", r"parameter", 2.0, 3))
pgm.add_node(daft.Node("observations", r"observations", 2.0, 2))
pgm.add_node(daft.Node("mu_sigma", r"$\mu,\sigma^2$", 5.5, 4))
pgm.add_node(daft.Node("theta_0", r"$\theta_0$", 4, 3))
pgm.add_node(daft.Node("theta_1", r"$\theta_1$", 5, 3))
pgm.add_node(daft.Node("theta_dots", r"$\cdots$", 6, 3))
pgm.add_node(daft.Node("theta_k", r"$\theta_k$", 7, 3))
pgm.add_node(daft.Node("y_0", r"$y_0$", 4, 2))
pgm.add_node(daft.Node("y_1", r"$y_1$", 5, 2))
pgm.add_node(daft.Node("y_dots", r"$\cdots$", 6, 2))
pgm.add_node(daft.Node("y_k", r"$y_k$", 7, 2))
pgm.add_edge("mu_sigma", "theta_0")
pgm.add_edge("mu_sigma", "theta_1")
pgm.add_edge("mu_sigma", "theta_k")
pgm.add_edge("theta_0", "y_0")
pgm.add_edge("theta_1", "y_1")
pgm.add_edge("theta_k", "y_k")
pgm.render()
plt.show()
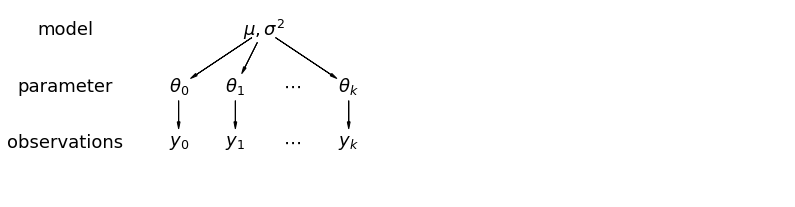
5.1 부분 풀링
가정용 라돈 데이터 세트에 대한 가장 간단한 부분 풀링 모델은 그룹이나 개인 수준에서 예측 변수 없이 단순히 라돈 수준을 추정하는 모델입니다. 개별 수준 예측 변수의 예는 데이터 포인트가 지하 또는 1층에 있는지 여부입니다. 그룹 수준 예측 변수는 카운티 전체 평균 우라늄 수준이 될 수 있습니다.
부분 풀링 모델은 풀링 및 풀링되지 않은 극단값 사이의 절충안, 풀링되지 않은 카운티 추정치와 풀링된 추정치의 대략 가중 평균(표본 크기 기반)을 나타냅니다.
하자 \(\hat{\alpha}_j\) 카운티에서의 추정 로그 라돈 수준이 될 \(j\). 가로채기일 뿐입니다. 우리는 지금 슬로프를 무시합니다. \(n_j\) 카운티에서 관찰의 수입니다 \(j\). \(\sigma_{\alpha}\) 및 \(\sigma_y\) 파라미터 내의 각각 분산 샘플링 분산이다. 그런 다음 부분 풀링 모델은 다음을 가정할 수 있습니다.
\[\hat{\alpha}_j \approx \frac{(n_j/\sigma_y^2)\bar{y}_j + (1/\sigma_{\alpha}^2)\bar{y} }{(n_j/\sigma_y^2) + (1/\sigma_{\alpha}^2)}\]
부분 풀링을 사용할 때 다음을 기대합니다.
- 표본 크기가 더 작은 카운티에 대한 추정치는 주 전체 평균으로 축소됩니다.
- 표본 크기가 더 큰 카운티에 대한 추정치는 풀링되지 않은 카운티 추정치에 더 가깝습니다.
mpl.rc("font", size=12)
pgm = daft.PGM([7, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"mu_a_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
3,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4,
3,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("mu_a", r"$\mu_a$", 1, 3))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{N}$", 2, 2, scale=1.25))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 3.25, 1, scale=1.25, observed=True))
pgm.add_edge("mu_a_prior", "mu_a")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("mu_a", "a")
pgm.add_edge("sigma_a", "a")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_plate(daft.Plate([1.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([2.65, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
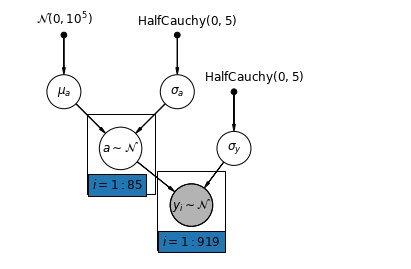
def partial_pooling_model(county):
"""Creates a joint distribution for the partial pooling model."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # mu_a
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a, mu_a: tfd.MultivariateNormalDiag( # a
loc=mu_a[..., tf.newaxis] * tf.ones([num_counties])[tf.newaxis, ...],
scale_identity_multiplier=sigma_a),
tfd.HalfCauchy(loc=0., scale=5), # sigma_y
lambda sigma_y, a: tfd.MultivariateNormalDiag( # y
loc=tf.gather(a, county, axis=-1),
scale_identity_multiplier=sigma_y)
])
@tf.function
def partial_pooling_log_prob(mu_a, sigma_a, a, sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return partial_pooling_model(county).log_prob(
[mu_a, sigma_a, a, sigma_y, log_radon])
@tf.function
def sample_partial_pooling(num_chains, num_results, num_burnin_steps):
"""Samples from the partial pooling model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=partial_pooling_log_prob,
num_leapfrog_steps=10,
step_size=0.01)
initial_state = [
tf.zeros([num_chains], name='init_mu_a'),
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='init_a'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Identity(), # mu_a
tfb.Exp(), # sigma_a
tfb.Identity(), # a
tfb.Exp() # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
PartialPoolingModel = collections.namedtuple(
'PartialPoolingModel', ['mu_a', 'sigma_a', 'a', 'sigma_y'])
samples, acceptance_probs = sample_partial_pooling(
num_chains=4, num_results=1000, num_burnin_steps=1000)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
partial_pooling_samples = PartialPoolingModel._make(samples)
Acceptance Probabilities: [0.989 0.977 0.988 0.985]
for var in ['mu_a', 'sigma_a', 'sigma_y']:
print(
'R-hat for ', var, '\t:',
tfp.mcmc.potential_scale_reduction(getattr(partial_pooling_samples,
var)).numpy())
R-hat for mu_a : 1.0216417 R-hat for sigma_a : 1.0224565 R-hat for sigma_y : 1.0016255
partial_pooling_intercepts = reduce_samples(
partial_pooling_samples.a.numpy(), np.mean)
partial_pooling_intercepts_se = reduce_samples(
partial_pooling_samples.a.numpy(), np.std)
def plot_unpooled_vs_partial_pooling_estimates():
fig, axes = plt.subplots(1, 2, figsize=(14, 6), sharex=True, sharey=True)
# Order counties by number of observations (and add some jitter).
num_obs_per_county = (
radon.groupby('county')['idnum'].count().values.astype(np.float32))
num_obs_per_county += np.random.normal(scale=0.5, size=num_counties)
intercepts_list = [unpooled_intercepts, partial_pooling_intercepts]
intercepts_se_list = [unpooled_intercepts_se, partial_pooling_intercepts_se]
for ax, means, std_errors in zip(axes, intercepts_list, intercepts_se_list):
ax.plot(num_obs_per_county, means, 'C0.')
for n, m, se in zip(num_obs_per_county, means, std_errors):
ax.plot([n, n], [m - se, m + se], 'C1-', alpha=.5)
for ax in axes:
ax.set_xscale('log')
ax.set_xlabel('No. of Observations Per County')
ax.set_xlim(1, 100)
ax.set_ylabel('Log Radon Estimate (with Standard Error)')
ax.set_ylim(0, 3)
ax.hlines(partial_pooling_intercepts.mean(), .9, 125, 'k', '--', alpha=.5)
axes[0].set_title('Unpooled Estimates')
axes[1].set_title('Partially Pooled Estimates')
plot_unpooled_vs_partial_pooling_estimates()
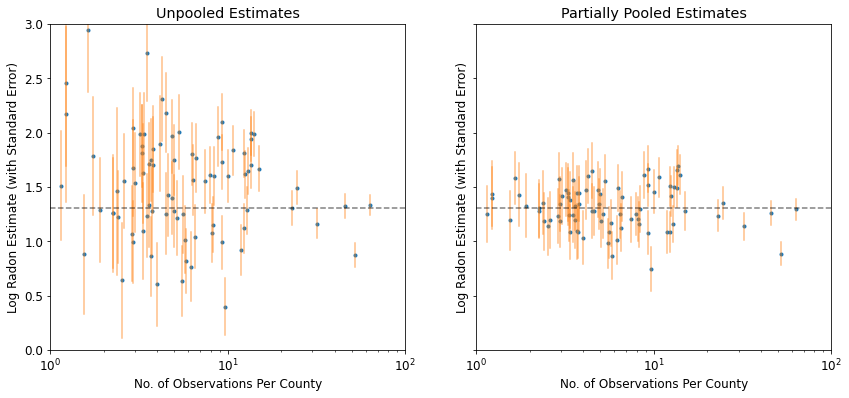
특히 더 작은 표본 크기에서 풀링되지 않은 추정값과 부분적으로 풀링된 추정값의 차이를 확인하십시오. 전자는 더 극단적이고 더 부정확합니다.
5.2 다양한 절편
이제 무작위 효과에 따라 카운티마다 가로채기를 허용하는 보다 복잡한 모델을 고려합니다.
\(y_i = \alpha_{j[i]} + \beta x_{i} + \epsilon_i\) 곳\(\epsilon_i \sim N(0, \sigma_y^2)\) 및 절편 임의 효과 :
\[\alpha_{j[i]} \sim N(\mu_{\alpha}, \sigma_{\alpha}^2)\]
기울기 \(\beta\)관찰을 측정 (또는 제 지하 층)의 위치에 따라 변할 수 있도록, 여전히 다른 군 사이에서 공유 고정 효과이다.
하여 unpooling 모델과 마찬가지로, 우리는 각 카운티에 대해 별도의 차단을 설정, 오히려 약간의 데이터 군에서 더 합리적인 추론을 허용 군 중에서 각 카운티, 다단계 모델링 주 강도에 대해 별도의 최소 제곱 회귀 모델을 맞는 것보다.
mpl.rc("font", size=12)
pgm = daft.PGM([7, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"mu_a_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
3,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(
daft.Node(
"b_prior",
r"$\mathcal{N}(0, 10^5)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("b", r"$b$", 4, 2.5))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
6,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("mu_a", r"$\mu_a$", 1, 3))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{N}$", 2, 2, scale=1.25))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 6, 2.5))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("mu_a_prior", "mu_a")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("mu_a", "a")
pgm.add_edge("b_prior", "b")
pgm.add_edge("sigma_a", "a")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([1.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
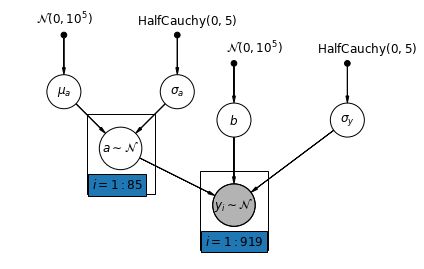
def varying_intercept_model(floor, county):
"""Creates a joint distribution for the varying intercept model."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # mu_a
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a, mu_a: tfd.MultivariateNormalDiag( # a
loc=affine(tf.ones([num_counties]), mu_a[..., tf.newaxis]),
scale_identity_multiplier=sigma_a),
tfd.Normal(loc=0., scale=1e5), # b
tfd.HalfCauchy(loc=0., scale=5), # sigma_y
lambda sigma_y, b, a: tfd.MultivariateNormalDiag( # y
loc=affine(floor, b[..., tf.newaxis], tf.gather(a, county, axis=-1)),
scale_identity_multiplier=sigma_y)
])
def varying_intercept_log_prob(mu_a, sigma_a, a, b, sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return varying_intercept_model(floor, county).log_prob(
[mu_a, sigma_a, a, b, sigma_y, log_radon])
@tf.function
def sample_varying_intercepts(num_chains, num_results, num_burnin_steps):
"""Samples from the varying intercepts model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=varying_intercept_log_prob,
num_leapfrog_steps=10,
step_size=0.01)
initial_state = [
tf.zeros([num_chains], name='init_mu_a'),
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='init_a'),
tf.zeros([num_chains], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Identity(), # mu_a
tfb.Exp(), # sigma_a
tfb.Identity(), # a
tfb.Identity(), # b
tfb.Exp() # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
VaryingInterceptsModel = collections.namedtuple(
'VaryingInterceptsModel', ['mu_a', 'sigma_a', 'a', 'b', 'sigma_y'])
samples, acceptance_probs = sample_varying_intercepts(
num_chains=4, num_results=1000, num_burnin_steps=1000)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
varying_intercepts_samples = VaryingInterceptsModel._make(samples)
Acceptance Probabilities: [0.978 0.987 0.982 0.984]
for var in ['mu_a', 'sigma_a', 'b', 'sigma_y']:
print(
'R-hat for ', var, ': ',
tfp.mcmc.potential_scale_reduction(
getattr(varying_intercepts_samples, var)).numpy())
R-hat for mu_a : 1.1099764 R-hat for sigma_a : 1.1058794 R-hat for b : 1.0448593 R-hat for sigma_y : 1.0019052
varying_intercepts_estimates = LinearEstimates(
sample_mean(varying_intercepts_samples.a),
sample_mean(varying_intercepts_samples.b))
sample_counties = ('Lac Qui Parle', 'Aitkin', 'Koochiching', 'Douglas', 'Clay',
'Stearns', 'Ramsey', 'St Louis')
plot_estimates(
linear_estimates=[
unpooled_estimates, pooled_estimate, varying_intercepts_estimates
],
labels=['Unpooled', 'Pooled', 'Varying Intercepts'],
sample_counties=sample_counties)
def plot_posterior(var_name, var_samples):
if isinstance(var_samples, tf.Tensor):
var_samples = var_samples.numpy() # convert to numpy array
fig = plt.figure(figsize=(10, 3))
ax = fig.add_subplot(111)
ax.hist(var_samples.flatten(), bins=40, edgecolor='white')
sample_mean = var_samples.mean()
ax.text(
sample_mean,
100,
'mean={:.3f}'.format(sample_mean),
color='white',
fontsize=12)
ax.set_xlabel('posterior of ' + var_name)
plt.show()
plot_posterior('b', varying_intercepts_samples.b)
plot_posterior('sigma_a', varying_intercepts_samples.sigma_a)
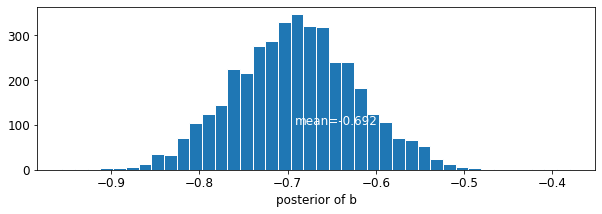
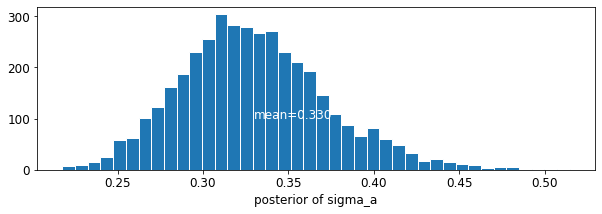
바닥 계수의 추정값은 대략 절반 (약 갖는 지하 집없이 해석 될 수 -0.69이다\(\exp(-0.69) = 0.50\)군 차지 후) 지하와 이들의 라돈 수준.
for var in ['b']:
var_samples = getattr(varying_intercepts_samples, var)
mean = var_samples.numpy().mean()
std = var_samples.numpy().std()
r_hat = tfp.mcmc.potential_scale_reduction(var_samples).numpy()
n_eff = tfp.mcmc.effective_sample_size(var_samples).numpy().sum()
print('var: ', var, ' mean: ', mean, ' std: ', std, ' n_eff: ', n_eff,
' r_hat: ', r_hat)
var: b mean: -0.6972574 std: 0.06966117 n_eff: 397.94327 r_hat: 1.0448593
def plot_intercepts_and_slopes(linear_estimates, title):
xvals = np.arange(2)
intercepts = np.ones([num_counties]) * linear_estimates.intercept
slopes = np.ones([num_counties]) * linear_estimates.slope
fig, ax = plt.subplots()
for c in range(num_counties):
ax.plot(xvals, intercepts[c] + slopes[c] * xvals, 'bo-', alpha=0.4)
plt.xlim(-0.2, 1.2)
ax.set_xticks([0, 1])
ax.set_xticklabels(['Basement', 'First Floor'])
ax.set_ylabel('Log Radon level')
plt.title(title)
plt.show()
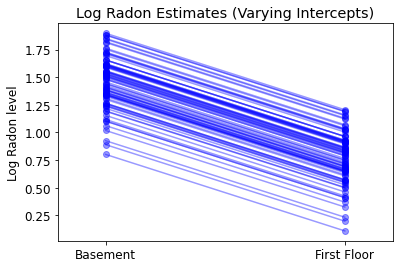
plot_intercepts_and_slopes(varying_intercepts_estimates,
'Log Radon Estimates (Varying Intercepts)')
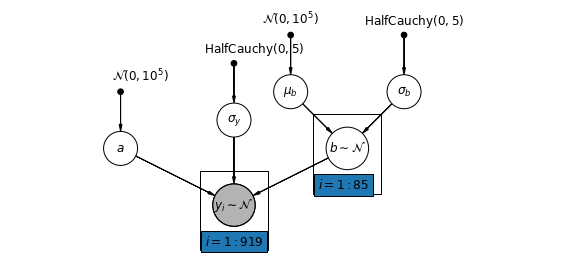
5.3 다양한 슬로프
또는 측정 위치(지하 또는 1층)가 라돈 수치에 미치는 영향에 따라 카운티가 달라지도록 하는 모델을 가정할 수 있습니다. 이 경우 요격 \(\alpha\) 군 사이에 공유됩니다.
\[y_i = \alpha + \beta_{j[i]} x_{i} + \epsilon_i\]
mpl.rc("font", size=12)
pgm = daft.PGM([10, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"mu_b_prior",
r"$\mathcal{N}(0, 10^5)$",
3.2,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"a_prior", r"$\mathcal{N}(0, 10^5)$", 2, 3, fixed=True, offset=(20, 5)))
pgm.add_node(daft.Node("a", r"$a$", 2, 2))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2.5))
pgm.add_node(
daft.Node(
"mu_b_prior",
r"$\mathcal{N}(0, 10^5)$",
5,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_b_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
7,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("mu_b", r"$\mu_b$", 5, 3))
pgm.add_node(daft.Node("sigma_b", r"$\sigma_b$", 7, 3))
pgm.add_node(daft.Node("b", r"$b \sim \mathcal{N}$", 6, 2, scale=1.25))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("a_prior", "a")
pgm.add_edge("mu_b_prior", "mu_b")
pgm.add_edge("sigma_b_prior", "sigma_b")
pgm.add_edge("mu_b", "b")
pgm.add_edge("sigma_b", "b")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([5.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
def varying_slopes_model(floor, county):
"""Creates a joint distribution for the varying slopes model."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # mu_b
tfd.HalfCauchy(loc=0., scale=5), # sigma_b
tfd.Normal(loc=0., scale=1e5), # a
lambda _, sigma_b, mu_b: tfd.MultivariateNormalDiag( # b
loc=affine(tf.ones([num_counties]), mu_b[..., tf.newaxis]),
scale_identity_multiplier=sigma_b),
tfd.HalfCauchy(loc=0., scale=5), # sigma_y
lambda sigma_y, b, a: tfd.MultivariateNormalDiag( # y
loc=affine(floor, tf.gather(b, county, axis=-1), a[..., tf.newaxis]),
scale_identity_multiplier=sigma_y)
])
def varying_slopes_log_prob(mu_b, sigma_b, a, b, sigma_y):
return varying_slopes_model(floor, county).log_prob(
[mu_b, sigma_b, a, b, sigma_y, log_radon])
@tf.function
def sample_varying_slopes(num_chains, num_results, num_burnin_steps):
"""Samples from the varying slopes model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=varying_slopes_log_prob,
num_leapfrog_steps=25,
step_size=0.01)
initial_state = [
tf.zeros([num_chains], name='init_mu_b'),
tf.ones([num_chains], name='init_sigma_b'),
tf.zeros([num_chains], name='init_a'),
tf.zeros([num_chains, num_counties], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Identity(), # mu_b
tfb.Exp(), # sigma_b
tfb.Identity(), # a
tfb.Identity(), # b
tfb.Exp() # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
VaryingSlopesModel = collections.namedtuple(
'VaryingSlopesModel', ['mu_b', 'sigma_b', 'a', 'b', 'sigma_y'])
samples, acceptance_probs = sample_varying_slopes(
num_chains=4, num_results=1000, num_burnin_steps=1000)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
varying_slopes_samples = VaryingSlopesModel._make(samples)
Acceptance Probabilities: [0.979 0.984 0.977 0.984]
for var in ['mu_b', 'sigma_b', 'a', 'sigma_y']:
print(
'R-hat for ', var, '\t: ',
tfp.mcmc.potential_scale_reduction(getattr(varying_slopes_samples,
var)).numpy())
R-hat for mu_b : 1.0770341 R-hat for sigma_b : 1.0634488 R-hat for a : 1.0133665 R-hat for sigma_y : 1.0011941
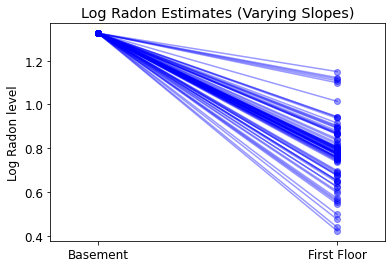
varying_slopes_estimates = LinearEstimates(
sample_mean(varying_slopes_samples.a),
sample_mean(varying_slopes_samples.b))
plot_intercepts_and_slopes(varying_slopes_estimates,
'Log Radon Estimates (Varying Slopes)')
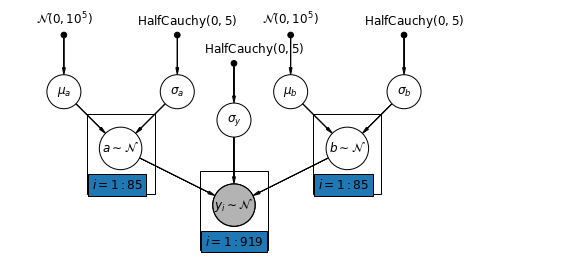
5.4 절편과 기울기의 변화
가장 일반적인 모델은 절편과 기울기가 카운티별로 다를 수 있습니다.
\[y_i = \alpha_{j[i]} + \beta_{j[i]} x_{i} + \epsilon_i\]
mpl.rc("font", size=12)
pgm = daft.PGM([10, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"mu_a_prior",
r"$\mathcal{N}(0, 10^5)$",
1,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
3,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("mu_a", r"$\mu_a$", 1, 3))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{N}$", 2, 2, scale=1.25))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2.5))
pgm.add_node(
daft.Node(
"mu_b_prior",
r"$\mathcal{N}(0, 10^5)$",
5,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"sigma_b_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
7,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("mu_b", r"$\mu_b$", 5, 3))
pgm.add_node(daft.Node("sigma_b", r"$\sigma_b$", 7, 3))
pgm.add_node(daft.Node("b", r"$b \sim \mathcal{N}$", 6, 2, scale=1.25))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("mu_a_prior", "mu_a")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("mu_a", "a")
pgm.add_edge("sigma_a", "a")
pgm.add_edge("mu_b_prior", "mu_b")
pgm.add_edge("sigma_b_prior", "sigma_b")
pgm.add_edge("mu_b", "b")
pgm.add_edge("sigma_b", "b")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([1.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([5.4, 1.2, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
def varying_intercepts_and_slopes_model(floor, county):
"""Creates a joint distribution for the varying slope model."""
return tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=1e5), # mu_a
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
tfd.Normal(loc=0., scale=1e5), # mu_b
tfd.HalfCauchy(loc=0., scale=5), # sigma_b
lambda sigma_b, mu_b, sigma_a, mu_a: tfd.MultivariateNormalDiag( # a
loc=affine(tf.ones([num_counties]), mu_a[..., tf.newaxis]),
scale_identity_multiplier=sigma_a),
lambda _, sigma_b, mu_b: tfd.MultivariateNormalDiag( # b
loc=affine(tf.ones([num_counties]), mu_b[..., tf.newaxis]),
scale_identity_multiplier=sigma_b),
tfd.HalfCauchy(loc=0., scale=5), # sigma_y
lambda sigma_y, b, a: tfd.MultivariateNormalDiag( # y
loc=affine(floor, tf.gather(b, county, axis=-1),
tf.gather(a, county, axis=-1)),
scale_identity_multiplier=sigma_y)
])
@tf.function
def varying_intercepts_and_slopes_log_prob(mu_a, sigma_a, mu_b, sigma_b, a, b,
sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return varying_intercepts_and_slopes_model(floor, county).log_prob(
[mu_a, sigma_a, mu_b, sigma_b, a, b, sigma_y, log_radon])
@tf.function
def sample_varying_intercepts_and_slopes(num_chains, num_results,
num_burnin_steps):
"""Samples from the varying intercepts and slopes model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=varying_intercepts_and_slopes_log_prob,
num_leapfrog_steps=50,
step_size=0.01)
initial_state = [
tf.zeros([num_chains], name='init_mu_a'),
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains], name='init_mu_b'),
tf.ones([num_chains], name='init_sigma_b'),
tf.zeros([num_chains, num_counties], name='init_a'),
tf.zeros([num_chains, num_counties], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Identity(), # mu_a
tfb.Exp(), # sigma_a
tfb.Identity(), # mu_b
tfb.Exp(), # sigma_b
tfb.Identity(), # a
tfb.Identity(), # b
tfb.Exp() # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
VaryingInterceptsAndSlopesModel = collections.namedtuple(
'VaryingInterceptsAndSlopesModel',
['mu_a', 'sigma_a', 'mu_b', 'sigma_b', 'a', 'b', 'sigma_y'])
samples, acceptance_probs = sample_varying_intercepts_and_slopes(
num_chains=4, num_results=1000, num_burnin_steps=500)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
varying_intercepts_and_slopes_samples = VaryingInterceptsAndSlopesModel._make(
samples)
Acceptance Probabilities: [0.988 0.985 0.992 0.938]
for var in ['mu_a', 'sigma_a', 'mu_b', 'sigma_b']:
print(
'R-hat for ', var, '\t: ',
tfp.mcmc.potential_scale_reduction(
getattr(varying_intercepts_and_slopes_samples, var)).numpy())
R-hat for mu_a : 1.010764 R-hat for sigma_a : 1.0078123 R-hat for mu_b : 1.0279609 R-hat for sigma_b : 1.3165458
varying_intercepts_and_slopes_estimates = LinearEstimates(
sample_mean(varying_intercepts_and_slopes_samples.a),
sample_mean(varying_intercepts_and_slopes_samples.b))
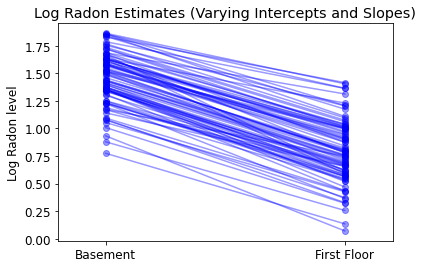
plot_intercepts_and_slopes(
varying_intercepts_and_slopes_estimates,
'Log Radon Estimates (Varying Intercepts and Slopes)')
forest_plot(
num_chains=4,
num_vars=num_counties,
var_name='a',
var_labels=county_name,
samples=varying_intercepts_and_slopes_samples.a.numpy())
forest_plot(
num_chains=4,
num_vars=num_counties,
var_name='b',
var_labels=county_name,
samples=varying_intercepts_and_slopes_samples.b.numpy())


6 그룹 수준 예측자 추가
다중 수준 모델의 주요 장점은 여러 수준의 예측 변수를 동시에 처리할 수 있다는 것입니다. 위의 가변 절편 모델을 고려하면:
\(y_i = \alpha_{j[i]} + \beta x_{i} + \epsilon_i\) 우리가 대신 간단한 임의 효과, 예상되는 라돈 값의 변화를 설명 카운티 수준의 공변량 또 다른 회귀 모델을 지정할 수 있습니다. 여기, 우리는 독서 카운티 우라늄 사용 \(u_j\)라돈 수준으로 관련이있는 것으로 생각된다 :
\(\alpha_j = \gamma_0 + \gamma_1 u_j + \zeta_j\)\(\zeta_j \sim N(0, \sigma_{\alpha}^2)\) 따라서, 우리는 이제 집 수준의 예측 (바닥이나 지하)뿐만 아니라 카운티 수준의 예측 (우라늄)를 포함한다.
모델에는 각 카운티에 대한 두 지표 변수와 카운티 수준 공변량이 있습니다. 고전적 회귀에서는 공선성이 발생합니다. 다중 수준 모델에서 그룹 수준 선형 모델의 예상 값을 향한 절편의 부분 풀링은 이를 방지합니다.
그룹 수준의 예측은 그룹 수준의 변화 감소하는 역할을\(\sigma_{\alpha}\). 이것의 중요한 의미는 그룹 수준 추정이 더 강력한 풀링을 유도한다는 것입니다.
6.1 계층적 절편 모델
mpl.rc("font", size=12)
pgm = daft.PGM([10, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"gamma_0_prior",
r"$\mathcal{N}(0, 10^5)$",
0.5,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(
daft.Node(
"gamma_1_prior",
r"$\mathcal{N}(0, 10^5)$",
1.5,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("gamma_0", r"$\gamma_0$", 0.5, 3))
pgm.add_node(daft.Node("gamma_1", r"$\gamma_1$", 1.5, 3))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathcal{N}(0, 10^5)$",
3,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3.5))
pgm.add_node(daft.Node("eps_a", r"$eps_a$", 3, 2.5, scale=1.25))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{Det}$", 1.5, 1.2, scale=1.5))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{U}(0, 100)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2.5))
pgm.add_node(daft.Node("b_prior", r"$\mathcal{N}(0, 10^5)$", 5, 3, fixed=True))
pgm.add_node(daft.Node("b", r"$b$", 5, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("gamma_0_prior", "gamma_0")
pgm.add_edge("gamma_1_prior", "gamma_1")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("sigma_a", "eps_a")
pgm.add_edge("gamma_0", "a")
pgm.add_edge("gamma_1", "a")
pgm.add_edge("eps_a", "a")
pgm.add_edge("b_prior", "b")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([2.4, 1.7, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([0.9, 0.4, 1.2, 1.4], "$i = 1:919$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
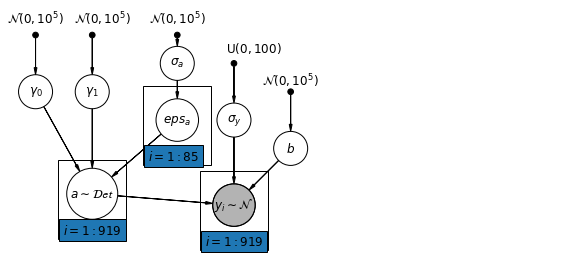
def hierarchical_intercepts_model(floor, county, log_uranium):
"""Creates a joint distribution for the varying slope model."""
return tfd.JointDistributionSequential([
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a: tfd.MultivariateNormalDiag( # eps_a
loc=tf.zeros([num_counties]),
scale_identity_multiplier=sigma_a),
tfd.Normal(loc=0., scale=1e5), # gamma_0
tfd.Normal(loc=0., scale=1e5), # gamma_1
tfd.Normal(loc=0., scale=1e5), # b
tfd.Uniform(low=0., high=100), # sigma_y
lambda sigma_y, b, gamma_1, gamma_0, eps_a: tfd.
MultivariateNormalDiag( # y
loc=affine(
floor, b[..., tf.newaxis],
affine(log_uranium, gamma_1[..., tf.newaxis],
gamma_0[..., tf.newaxis]) + tf.gather(eps_a, county, axis=-1)),
scale_identity_multiplier=sigma_y)
])
def hierarchical_intercepts_log_prob(sigma_a, eps_a, gamma_0, gamma_1, b,
sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return hierarchical_intercepts_model(floor, county, log_uranium).log_prob(
[sigma_a, eps_a, gamma_0, gamma_1, b, sigma_y, log_radon])
@tf.function
def sample_hierarchical_intercepts(num_chains, num_results, num_burnin_steps):
"""Samples from the hierarchical intercepts model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=hierarchical_intercepts_log_prob,
num_leapfrog_steps=10,
step_size=0.01)
initial_state = [
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='eps_a'),
tf.zeros([num_chains], name='init_gamma_0'),
tf.zeros([num_chains], name='init_gamma_1'),
tf.zeros([num_chains], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Exp(), # sigma_a
tfb.Identity(), # eps_a
tfb.Identity(), # gamma_0
tfb.Identity(), # gamma_0
tfb.Identity(), # b
# Maps reals to [0, 100].
tfb.Chain([tfb.Shift(shift=50.),
tfb.Scale(scale=50.),
tfb.Tanh()]) # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
HierarchicalInterceptsModel = collections.namedtuple(
'HierarchicalInterceptsModel',
['sigma_a', 'eps_a', 'gamma_0', 'gamma_1', 'b', 'sigma_y'])
samples, acceptance_probs = sample_hierarchical_intercepts(
num_chains=4, num_results=2000, num_burnin_steps=500)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
hierarchical_intercepts_samples = HierarchicalInterceptsModel._make(samples)
Acceptance Probabilities: [0.9615 0.941 0.955 0.95 ]
for var in ['sigma_a', 'gamma_0', 'gamma_1', 'b', 'sigma_y']:
print(
'R-hat for', var, ':',
tfp.mcmc.potential_scale_reduction(
getattr(hierarchical_intercepts_samples, var)).numpy())
R-hat for sigma_a : 1.0469627 R-hat for gamma_0 : 1.0016835 R-hat for gamma_1 : 1.0097923 R-hat for b : 1.0014259 R-hat for sigma_y : 1.0025403
def plot_hierarchical_intercepts():
mean_and_var = lambda x : [reduce_samples(x, fn) for fn in [np.mean, np.var]]
gamma_0_mean, gamma_0_var = mean_and_var(
hierarchical_intercepts_samples.gamma_0)
gamma_1_mean, gamma_1_var = mean_and_var(
hierarchical_intercepts_samples.gamma_1)
eps_a_means, eps_a_vars = mean_and_var(hierarchical_intercepts_samples.eps_a)
mu_a_means = gamma_0_mean + gamma_1_mean * log_uranium
mu_a_vars = gamma_0_var + np.square(log_uranium) * gamma_1_var
a_means = mu_a_means + eps_a_means[county]
a_stds = np.sqrt(mu_a_vars + eps_a_vars[county])
plt.figure()
plt.scatter(log_uranium, a_means, marker='.', c='C0')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,gamma_0_mean + gamma_1_mean * xvals, 'k--')
plt.xlim(-1, 0.8)
for ui, m, se in zip(log_uranium, a_means, a_stds):
plt.plot([ui, ui], [m - se, m + se], 'C1-', alpha=0.1)
plt.xlabel('County-level uranium')
plt.ylabel('Intercept estimate')
plot_hierarchical_intercepts()
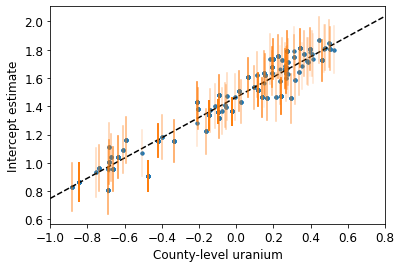
절편의 표준 오차는 카운티 수준 공변량이 없는 부분 풀링 모델보다 좁습니다.
6.2 레벨 간의 상관관계
경우에 따라 여러 수준의 예측 변수를 사용하면 개별 수준 변수와 그룹 잔차 간의 상관 관계가 드러날 수 있습니다. 개별 예측 변수의 평균을 그룹 절편에 대한 모델의 공변량으로 포함하여 이를 설명할 수 있습니다.
\(\alpha_j = \gamma_0 + \gamma_1 u_j + \gamma_2 \bar{x} + \zeta_j\) 이들은 넓은 문맥 효과라고 칭한다.
mpl.rc("font", size=12)
pgm = daft.PGM([10, 4.5], node_unit=1.2)
pgm.add_node(
daft.Node(
"gamma_prior",
r"$\mathcal{N}(0, 10^5)$",
1.5,
4,
fixed=True,
offset=(10, 5)))
pgm.add_node(daft.Node("gamma", r"$\gamma$", 1.5, 3.5))
pgm.add_node(daft.Node("mu_a", r"$\mu_a$", 1.5, 2.2))
pgm.add_node(
daft.Node(
"sigma_a_prior",
r"$\mathrm{HalfCauchy}(0, 5)$",
3,
4,
fixed=True,
offset=(0, 5)))
pgm.add_node(daft.Node("sigma_a", r"$\sigma_a$", 3, 3.5))
pgm.add_node(daft.Node("eps_a", r"$eps_a$", 3, 2.5, scale=1.25))
pgm.add_node(daft.Node("a", r"$a \sim \mathcal{Det}$", 1.5, 1.2, scale=1.5))
pgm.add_node(
daft.Node(
"sigma_prior",
r"$\mathrm{U}(0, 100)$",
4,
3.5,
fixed=True,
offset=(20, 5)))
pgm.add_node(daft.Node("sigma_y", r"$\sigma_y$", 4, 2.5))
pgm.add_node(daft.Node("b_prior", r"$\mathcal{N}(0, 10^5)$", 5, 3, fixed=True))
pgm.add_node(daft.Node("b", r"$b$", 5, 2))
pgm.add_node(
daft.Node(
"y_i", r"$y_i \sim \mathcal{N}$", 4, 1, scale=1.25, observed=True))
pgm.add_edge("gamma_prior", "gamma")
pgm.add_edge("sigma_a_prior", "sigma_a")
pgm.add_edge("sigma_a", "eps_a")
pgm.add_edge("gamma", "mu_a")
pgm.add_edge("mu_a", "a")
pgm.add_edge("eps_a", "a")
pgm.add_edge("b_prior", "b")
pgm.add_edge("sigma_prior", "sigma_y")
pgm.add_edge("sigma_y", "y_i")
pgm.add_edge("a", "y_i")
pgm.add_edge("b", "y_i")
pgm.add_plate(daft.Plate([0.9, 2.9, 1.2, 1.0], "$i = 1:3$"))
pgm.add_plate(daft.Plate([2.4, 1.7, 1.2, 1.4], "$i = 1:85$"))
pgm.add_plate(daft.Plate([0.9, 0.4, 1.2, 2.2], "$i = 1:919$"))
pgm.add_plate(daft.Plate([3.4, 0.2, 1.2, 1.4], "$i = 1:919$"))
pgm.render()
plt.show()
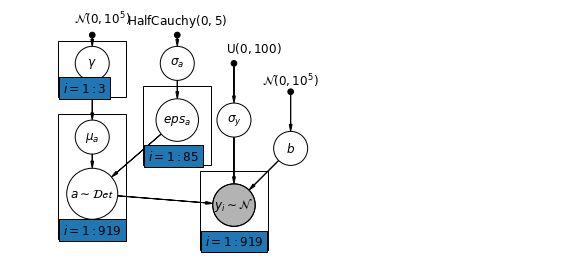
# Create a new variable for mean of floor across counties
xbar = tf.convert_to_tensor(radon.groupby('county')['floor'].mean(), tf.float32)
xbar = tf.gather(xbar, county, axis=-1)
def contextual_effects_model(floor, county, log_uranium, xbar):
"""Creates a joint distribution for the varying slope model."""
return tfd.JointDistributionSequential([
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a: tfd.MultivariateNormalDiag( # eps_a
loc=tf.zeros([num_counties]),
scale_identity_multiplier=sigma_a),
tfd.Normal(loc=0., scale=1e5), # gamma_0
tfd.Normal(loc=0., scale=1e5), # gamma_1
tfd.Normal(loc=0., scale=1e5), # gamma_2
tfd.Normal(loc=0., scale=1e5), # b
tfd.Uniform(low=0., high=100), # sigma_y
lambda sigma_y, b, gamma_2, gamma_1, gamma_0, eps_a: tfd.
MultivariateNormalDiag( # y
loc=affine(
floor, b[..., tf.newaxis],
affine(log_uranium, gamma_1[..., tf.newaxis], gamma_0[
..., tf.newaxis]) + affine(xbar, gamma_2[..., tf.newaxis]) +
tf.gather(eps_a, county, axis=-1)),
scale_identity_multiplier=sigma_y)
])
def contextual_effects_log_prob(sigma_a, eps_a, gamma_0, gamma_1, gamma_2, b,
sigma_y):
"""Computes joint log prob pinned at `log_radon`."""
return contextual_effects_model(floor, county, log_uranium, xbar).log_prob(
[sigma_a, eps_a, gamma_0, gamma_1, gamma_2, b, sigma_y, log_radon])
@tf.function
def sample_contextual_effects(num_chains, num_results, num_burnin_steps):
"""Samples from the hierarchical intercepts model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=contextual_effects_log_prob,
num_leapfrog_steps=10,
step_size=0.01)
initial_state = [
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='eps_a'),
tf.zeros([num_chains], name='init_gamma_0'),
tf.zeros([num_chains], name='init_gamma_1'),
tf.zeros([num_chains], name='init_gamma_2'),
tf.zeros([num_chains], name='init_b'),
tf.ones([num_chains], name='init_sigma_y')
]
unconstraining_bijectors = [
tfb.Exp(), # sigma_a
tfb.Identity(), # eps_a
tfb.Identity(), # gamma_0
tfb.Identity(), # gamma_1
tfb.Identity(), # gamma_2
tfb.Identity(), # b
tfb.Chain([tfb.Shift(shift=50.),
tfb.Scale(scale=50.),
tfb.Tanh()]) # sigma_y
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
ContextualEffectsModel = collections.namedtuple(
'ContextualEffectsModel',
['sigma_a', 'eps_a', 'gamma_0', 'gamma_1', 'gamma_2', 'b', 'sigma_y'])
samples, acceptance_probs = sample_contextual_effects(
num_chains=4, num_results=2000, num_burnin_steps=500)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
contextual_effects_samples = ContextualEffectsModel._make(samples)
Acceptance Probabilities: [0.9505 0.9595 0.951 0.9535]
for var in ['sigma_a', 'gamma_0', 'gamma_1', 'gamma_2', 'b', 'sigma_y']:
print(
'R-hat for ', var, ': ',
tfp.mcmc.potential_scale_reduction(
getattr(contextual_effects_samples, var)).numpy())
R-hat for sigma_a : 1.0709597 R-hat for gamma_0 : 1.0067923 R-hat for gamma_1 : 1.0089629 R-hat for gamma_2 : 1.0054177 R-hat for b : 1.0018929 R-hat for sigma_y : 1.0032713
for var in ['gamma_0', 'gamma_1', 'gamma_2']:
var_samples = getattr(contextual_effects_samples, var)
mean = var_samples.numpy().mean()
std = var_samples.numpy().std()
r_hat = tfp.mcmc.potential_scale_reduction(var_samples).numpy()
n_eff = tfp.mcmc.effective_sample_size(var_samples).numpy().sum()
print(var, ' mean: ', mean, ' std: ', std, ' n_eff: ', n_eff, ' r_hat: ',
r_hat)
gamma_0 mean: 1.3934746 std: 0.04966602 n_eff: 816.21265 r_hat: 1.0067923 gamma_1 mean: 0.7229424 std: 0.088611916 n_eff: 1462.486 r_hat: 1.0089629 gamma_2 mean: 0.40893936 std: 0.20304097 n_eff: 457.8165 r_hat: 1.0054177
따라서 지하실이 없는 주택의 비율이 높은 카운티는 기준선 수준의 라돈이 더 높은 경향이 있다는 것을 이로부터 추론할 수 있습니다. 아마도 이것은 건설되는 구조물의 유형에 영향을 미칠 수 있는 토양 유형과 관련이 있을 것입니다.
6.3 예측
Gelman(2006)은 교차 검증 테스트를 사용하여 풀링되지 않은 모델, 풀링된 모델 및 부분적으로 풀링된 모델의 예측 오류를 확인했습니다.
제곱 평균 제곱근 교차 검증 예측 오류:
- 풀링되지 않은 = 0.86
- 합동 = 0.84
- 다단계 = 0.79
다단계 모델에서 수행할 수 있는 예측에는 두 가지 유형이 있습니다.
- 기존 그룹 내의 새로운 개인
- 새 그룹 내의 새 개인
예를 들어, St. Louis 카운티에 지하실이 없는 새 집에 대한 예측을 하려면 적절한 절편을 사용하여 라돈 모델에서 샘플링하기만 하면 됩니다.
county_name.index('St Louis')
69
그건,
\[\tilde{y}_i \sim N(\alpha_{69} + \beta (x_i=1), \sigma_y^2)\]
st_louis_log_uranium = tf.convert_to_tensor(
radon.where(radon['county'] == 69)['log_uranium_ppm'].mean(), tf.float32)
st_louis_xbar = tf.convert_to_tensor(
radon.where(radon['county'] == 69)['floor'].mean(), tf.float32)
@tf.function
def intercept_a(gamma_0, gamma_1, gamma_2, eps_a, log_uranium, xbar, county):
return (affine(log_uranium, gamma_1, gamma_0) + affine(xbar, gamma_2) +
tf.gather(eps_a, county, axis=-1))
def contextual_effects_predictive_model(floor, county, log_uranium, xbar,
st_louis_log_uranium, st_louis_xbar):
"""Creates a joint distribution for the contextual effects model."""
return tfd.JointDistributionSequential([
tfd.HalfCauchy(loc=0., scale=5), # sigma_a
lambda sigma_a: tfd.MultivariateNormalDiag( # eps_a
loc=tf.zeros([num_counties]),
scale_identity_multiplier=sigma_a),
tfd.Normal(loc=0., scale=1e5), # gamma_0
tfd.Normal(loc=0., scale=1e5), # gamma_1
tfd.Normal(loc=0., scale=1e5), # gamma_2
tfd.Normal(loc=0., scale=1e5), # b
tfd.Uniform(low=0., high=100), # sigma_y
# y
lambda sigma_y, b, gamma_2, gamma_1, gamma_0, eps_a: (
tfd.MultivariateNormalDiag(
loc=affine(
floor, b[..., tf.newaxis],
intercept_a(gamma_0[..., tf.newaxis],
gamma_1[..., tf.newaxis], gamma_2[..., tf.newaxis],
eps_a, log_uranium, xbar, county)),
scale_identity_multiplier=sigma_y)),
# stl_pred
lambda _, sigma_y, b, gamma_2, gamma_1, gamma_0, eps_a: tfd.Normal(
loc=intercept_a(gamma_0, gamma_1, gamma_2, eps_a,
st_louis_log_uranium, st_louis_xbar, 69) + b,
scale=sigma_y)
])
@tf.function
def contextual_effects_predictive_log_prob(sigma_a, eps_a, gamma_0, gamma_1,
gamma_2, b, sigma_y, stl_pred):
"""Computes joint log prob pinned at `log_radon`."""
return contextual_effects_predictive_model(floor, county, log_uranium, xbar,
st_louis_log_uranium,
st_louis_xbar).log_prob([
sigma_a, eps_a, gamma_0,
gamma_1, gamma_2, b, sigma_y,
log_radon, stl_pred
])
@tf.function
def sample_contextual_effects_predictive(num_chains, num_results,
num_burnin_steps):
"""Samples from the contextual effects predictive model."""
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=contextual_effects_predictive_log_prob,
num_leapfrog_steps=50,
step_size=0.01)
initial_state = [
tf.ones([num_chains], name='init_sigma_a'),
tf.zeros([num_chains, num_counties], name='eps_a'),
tf.zeros([num_chains], name='init_gamma_0'),
tf.zeros([num_chains], name='init_gamma_1'),
tf.zeros([num_chains], name='init_gamma_2'),
tf.zeros([num_chains], name='init_b'),
tf.ones([num_chains], name='init_sigma_y'),
tf.zeros([num_chains], name='init_stl_pred')
]
unconstraining_bijectors = [
tfb.Exp(), # sigma_a
tfb.Identity(), # eps_a
tfb.Identity(), # gamma_0
tfb.Identity(), # gamma_1
tfb.Identity(), # gamma_2
tfb.Identity(), # b
tfb.Chain([tfb.Shift(shift=50.),
tfb.Scale(scale=50.),
tfb.Tanh()]), # sigma_y
tfb.Identity(), # stl_pred
]
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstraining_bijectors)
samples, kernel_results = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=initial_state,
kernel=kernel)
acceptance_probs = tf.reduce_mean(
tf.cast(kernel_results.inner_results.is_accepted, tf.float32), axis=0)
return samples, acceptance_probs
ContextualEffectsPredictiveModel = collections.namedtuple(
'ContextualEffectsPredictiveModel', [
'sigma_a', 'eps_a', 'gamma_0', 'gamma_1', 'gamma_2', 'b', 'sigma_y',
'stl_pred'
])
samples, acceptance_probs = sample_contextual_effects_predictive(
num_chains=4, num_results=2000, num_burnin_steps=500)
print('Acceptance Probabilities: ', acceptance_probs.numpy())
contextual_effects_pred_samples = ContextualEffectsPredictiveModel._make(
samples)
Acceptance Probabilities: [0.9165 0.978 0.9755 0.9785]
for var in [
'sigma_a', 'gamma_0', 'gamma_1', 'gamma_2', 'b', 'sigma_y', 'stl_pred'
]:
print(
'R-hat for ', var, ': ',
tfp.mcmc.potential_scale_reduction(
getattr(contextual_effects_pred_samples, var)).numpy())
R-hat for sigma_a : 1.0325582 R-hat for gamma_0 : 1.0033548 R-hat for gamma_1 : 1.0011047 R-hat for gamma_2 : 1.001153 R-hat for b : 1.0020066 R-hat for sigma_y : 1.0128921 R-hat for stl_pred : 1.0058256
plot_traces('stl_pred', contextual_effects_pred_samples.stl_pred, num_chains=4)

plot_posterior('stl_pred', contextual_effects_pred_samples.stl_pred)
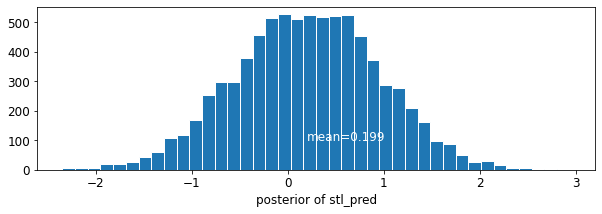
7 결론
다단계 모델의 이점:
- 관측 데이터의 자연스러운 계층 구조를 설명합니다.
- (과소 대표된) 그룹에 대한 계수 추정.
- 그룹 수준 계수를 추정할 때 개인 및 그룹 수준 정보를 통합합니다.
- 그룹 간의 개별 수준 계수 간의 변동을 허용합니다.
참고문헌
Gelman, A., & Hill, J. (2006). 회귀 및 다단계/계층적 모델을 사용한 데이터 분석(1판). 캠브리지 대학 출판부.
Gelman, A. (2006). 다단계(계층적) 모델링: 할 수 있는 것과 할 수 없는 것. 테크노메트릭스, 48(3), 432–435.
