 TensorFlow.org पर देखें TensorFlow.org पर देखें |  Google Colab में चलाएं Google Colab में चलाएं |  GitHub पर स्रोत देखें GitHub पर स्रोत देखें |  नोटबुक डाउनलोड करें नोटबुक डाउनलोड करें |
इस नोटबुक में, हम TensorFlow वितरण (संक्षेप में TFD) की खोज करेंगे। इस नोटबुक का लक्ष्य आपको सीखने की अवस्था को धीरे-धीरे ऊपर ले जाना है, जिसमें टीएफडी के टेंसर आकृतियों के संचालन को समझना भी शामिल है। यह नोटबुक अमूर्त अवधारणाओं के बजाय उदाहरण प्रस्तुत करने का प्रयास करती है। हम पहले काम करने के लिए कैननिकल आसान तरीके पेश करेंगे, और सबसे सामान्य अमूर्त दृश्य को अंत तक सहेजेंगे। आप प्रकार है जो एक अधिक अमूर्त और संदर्भ शैली ट्यूटोरियल पसंद कर रहे हैं, बाहर की जाँच को समझना TensorFlow वितरण आकृतियाँ । आप यहाँ सामग्री के बारे में कोई प्रश्न हैं, संपर्क करने में संकोच नहीं है (या सम्मिलित हों) TensorFlow संभावना मेलिंग सूची । हमें मदद करने में खुशी हो रही है.
शुरू करने से पहले, हमें उपयुक्त पुस्तकालयों को आयात करने की आवश्यकता है। हमारे समग्र पुस्तकालय है tensorflow_probability । परंपरा के अनुसार, हम आम तौर पर के रूप में वितरण पुस्तकालय का उल्लेख tfd ।
Tensorflow उत्सुक TensorFlow के लिए एक अनिवार्य निष्पादन माहौल है। TensorFlow में उत्सुक, प्रत्येक TF ऑपरेशन का तुरंत मूल्यांकन किया जाता है और परिणाम उत्पन्न करता है। यह TensorFlow के मानक "ग्राफ" मोड के विपरीत है, जिसमें TF संचालन एक ग्राफ में नोड्स जोड़ते हैं जिसे बाद में निष्पादित किया जाता है। यह पूरी नोटबुक TF Eager का उपयोग करके लिखी गई है, हालाँकि यहाँ प्रस्तुत कोई भी अवधारणा उस पर निर्भर नहीं करती है, और TFP का उपयोग ग्राफ़ मोड में किया जा सकता है।
import collections
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
try:
tf.compat.v1.enable_eager_execution()
except ValueError:
pass
import matplotlib.pyplot as plt
बेसिक यूनीवेरिएट डिस्ट्रीब्यूशन
आइए सही में गोता लगाएँ और एक सामान्य वितरण बनाएँ:
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
हम इसका एक नमूना ले सकते हैं:
n.sample()
<tf.Tensor: shape=(), dtype=float32, numpy=0.25322816>
हम कई नमूने खींच सकते हैं:
n.sample(3)
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4658079, -0.5653636, 0.9314412], dtype=float32)>
हम एक लॉग समस्या का मूल्यांकन कर सकते हैं:
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
हम कई लॉग संभावनाओं का मूल्यांकन कर सकते हैं:
n.log_prob([0., 2., 4.])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.9189385, -2.9189386, -8.918939 ], dtype=float32)>
हमारे पास वितरण की एक विस्तृत श्रृंखला है। आइए एक बर्नौली का प्रयास करें:
b = tfd.Bernoulli(probs=0.7)
b
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[] event_shape=[] dtype=int32>
b.sample()
<tf.Tensor: shape=(), dtype=int32, numpy=1>
b.sample(8)
<tf.Tensor: shape=(8,), dtype=int32, numpy=array([1, 0, 0, 0, 1, 0, 1, 0], dtype=int32)>
b.log_prob(1)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.35667497>
b.log_prob([1, 0, 1, 0])
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.35667497, -1.2039728 , -0.35667497, -1.2039728 ], dtype=float32)>
बहुभिन्नरूपी वितरण
हम एक विकर्ण सहप्रसरण के साथ एक बहुभिन्नरूपी सामान्य बनाएंगे:
nd = tfd.MultivariateNormalDiag(loc=[0., 10.], scale_diag=[1., 4.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
इसकी तुलना हमारे द्वारा पहले बनाए गए अविभाज्य सामान्य से की जाती है, क्या भिन्न है?
tfd.Normal(loc=0., scale=1.)
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
हम चाहते हैं कि univariate सामान्य एक है, यह देखने event_shape की () , जो यह दर्शाता है कि यह एक अदिश वितरण है। मल्टीवेरिएट सामान्य एक है event_shape की 2 , बुनियादी [घटना अंतरिक्ष] (https://en.wikipedia.org/wiki/Event_ (probability_theory)) इस वितरण के संकेत दो आयामी है।
नमूनाकरण पहले की तरह ही काम करता है:
nd.sample()
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.2489667, 15.025171 ], dtype=float32)>
nd.sample(5)
<tf.Tensor: shape=(5, 2), dtype=float32, numpy=
array([[-1.5439653 , 8.9968405 ],
[-0.38730723, 12.448896 ],
[-0.8697963 , 9.330035 ],
[-1.2541095 , 10.268944 ],
[ 2.3475595 , 13.184147 ]], dtype=float32)>
nd.log_prob([0., 10])
<tf.Tensor: shape=(), dtype=float32, numpy=-3.2241714>
बहुभिन्नरूपी मानदंडों में सामान्य रूप से विकर्ण सहप्रसरण नहीं होता है। TFD बहुभिन्नरूपी मानदंड बनाने के कई तरीके प्रदान करता है, जिसमें एक पूर्ण-सहप्रसरण विनिर्देश भी शामिल है, जिसका हम यहां उपयोग करते हैं।
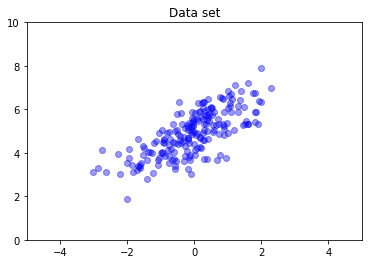
nd = tfd.MultivariateNormalFullCovariance(
loc = [0., 5], covariance_matrix = [[1., .7], [.7, 1.]])
data = nd.sample(200)
plt.scatter(data[:, 0], data[:, 1], color='blue', alpha=0.4)
plt.axis([-5, 5, 0, 10])
plt.title("Data set")
plt.show()
एकाधिक वितरण
हमारा पहला बर्नौली वितरण एक निष्पक्ष सिक्के के एक फ्लिप का प्रतिनिधित्व करता था। हम यह भी स्वतंत्र Bernoulli वितरण का एक बैच बना सकते हैं, अपने स्वयं के मानकों के साथ प्रत्येक, एक एकल में Distribution वस्तु:
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
इसका क्या अर्थ है, इस पर स्पष्ट होना महत्वपूर्ण है। ऊपर कॉल तीन स्वतंत्र Bernoulli वितरण, जो एक ही अजगर में समाहित किया जाना होता है परिभाषित करता Distribution वस्तु। तीन वितरणों को व्यक्तिगत रूप से हेरफेर नहीं किया जा सकता है। नोट कैसे batch_shape है (3,) , तीन वितरण का एक बैच का संकेत है, और event_shape है () , जो यह दर्शाता व्यक्तिगत वितरण एक univariate घटना जगह है।
अगर हम कहते हैं sample , हम तीनों से एक नमूना प्राप्त करें:
b3.sample()
<tf.Tensor: shape=(3,), dtype=int32, numpy=array([0, 1, 1], dtype=int32)>
b3.sample(6)
<tf.Tensor: shape=(6, 3), dtype=int32, numpy=
array([[1, 0, 1],
[0, 1, 1],
[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0]], dtype=int32)>
अगर हम कहते हैं prob , (यह रूप में एक ही आकार अर्थ विज्ञान है log_prob , हम का उपयोग prob स्पष्टता के लिए इन छोटे Bernoulli उदाहरण के साथ है, हालांकि log_prob आमतौर पर अनुप्रयोगों में पसंद किया जाता है) हम इसे एक वेक्टर पारित कर सकते हैं और कहा कि मूल्य उपज प्रत्येक सिक्का की संभावना का मूल्यांकन :
b3.prob([1, 1, 0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.29999998], dtype=float32)>
एपीआई में बैच आकार क्यों शामिल है? शब्दार्थ एक वितरण की एक सूची बनाने और उन पर एक साथ पुनरावृत्ति द्वारा एक ही संगणना प्रदर्शन कर सकता है for (यदि आप एक आवश्यकता होगी उत्सुक मोड में कम से कम TF ग्राफ मोड में, पाश tf.while पाश)। हालांकि, समान रूप से पैरामीटरयुक्त वितरणों का एक (संभावित रूप से बड़ा) सेट होना अत्यंत सामान्य है, और जब भी संभव हो वेक्टरकृत संगणनाओं का उपयोग हार्डवेयर त्वरक का उपयोग करके तेजी से गणना करने में सक्षम होने में एक प्रमुख घटक है।
घटनाओं के लिए स्वतंत्र से कुल बैचों का उपयोग करना
पिछले अनुभाग में, हम बनाया b3 , एक भी Distribution कि प्रतिनिधित्व किया तीन सिक्का उछालता वस्तु। अगर हम बुलाया b3.prob एक वेक्टर पर \(v\), \(i\)'वें प्रविष्टि संभावना है कि था \(i\)वें सिक्का मूल्य लेता \(v[i]\)।
मान लीजिए कि हम इसके बजाय एक ही अंतर्निहित परिवार से स्वतंत्र यादृच्छिक चर पर "संयुक्त" वितरण निर्दिष्ट करना चाहते हैं। यह एक अलग वस्तु गणितीय है, में है कि इस नए वितरण के लिए, prob एक वेक्टर पर \(v\) संभावना है कि सिक्के के पूरे सेट वेक्टर से मेल खाता है का प्रतिनिधित्व करने के लिए एक एकल मान प्रदान करेंगे \(v\)।
हम इसे कैसे पूरा करते हैं? हम एक "उच्च क्रम" वितरण कहा जाता है का उपयोग Independent है, जो एक वितरण लेता है और बैच आकार घटना आकार के लिए ले जाया के साथ एक नया वितरण पैदावार:
b3_joint = tfd.Independent(b3, reinterpreted_batch_ndims=1)
b3_joint
<tfp.distributions.Independent 'IndependentBernoulli' batch_shape=[] event_shape=[3] dtype=int32>
मूल की है कि आकार की तुलना करें b3 :
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
के रूप में वादा किया था, हम देखते हैं कि कि Independent घटना आकार में बैच आकार ले जाया गया है: b3_joint एक भी वितरण (है batch_shape = () ) एक तीन आयामी घटना अंतरिक्ष (अधिक event_shape = (3,) )।
आइए शब्दार्थ की जाँच करें:
b3_joint.prob([1, 1, 0])
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999998>
एक ही परिणाम प्राप्त करने के लिए एक वैकल्पिक तरीका का उपयोग कर गणना संभावनाओं होगा b3 और कमी (संक्षेप, या अधिक सामान्य मामले में जहां लॉग संभावनाओं का उपयोग किया जाता है,) गुणा करके मैन्युअल रूप से कार्य करें:
tf.reduce_prod(b3.prob([1, 1, 0]))
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999994>
Indpendent उपयोगकर्ता अधिक स्पष्ट रूप से वांछित अवधारणा का प्रतिनिधित्व करने की अनुमति देता है। हम इसे अत्यंत उपयोगी मानते हैं, हालांकि यह कड़ाई से आवश्यक नहीं है।
मजेदार तथ्य:
-
b3.sampleऔरb3_joint.sampleस्वतंत्र वितरण का एक बैच और का उपयोग कर बैच से स्वतः निर्मित एक भी वितरण के बीच अंतर: विभिन्न वैचारिक कार्यान्वयन, लेकिन पृथक outputs हैIndependentशो Probabilités कंप्यूटिंग, नहीं जब नमूने जब। -
MultivariateNormalDiagतुच्छता अदिश का उपयोग कर लागू किया जा सकताNormalऔरIndependentवितरण (यह वास्तव में इस तरह से लागू नहीं किया गया है, लेकिन यह हो सकता है)।
बहुभिन्नरूपी विक्षोभ के बैच
आइए तीन पूर्ण-सहप्रसरण द्वि-आयामी बहुभिन्नरूपी मानदंडों का एक बैच बनाएं:
nd_batch = tfd.MultivariateNormalFullCovariance(
loc = [[0., 0.], [1., 1.], [2., 2.]],
covariance_matrix = [[[1., .1], [.1, 1.]],
[[1., .3], [.3, 1.]],
[[1., .5], [.5, 1.]]])
nd_batch
<tfp.distributions.MultivariateNormalFullCovariance 'MultivariateNormalFullCovariance' batch_shape=[3] event_shape=[2] dtype=float32>
हम देखते हैं batch_shape = (3,) , इसलिए वहाँ तीन स्वतंत्र मल्टीवेरिएट normals हैं, और event_shape = (2,) है, इसलिए प्रत्येक मल्टीवेरिएट सामान्य दो आयामी है। इस उदाहरण में, व्यक्तिगत वितरण में स्वतंत्र तत्व नहीं होते हैं।
नमूनाकरण कार्य:
nd_batch.sample(4)
<tf.Tensor: shape=(4, 3, 2), dtype=float32, numpy=
array([[[ 0.7367498 , 2.730996 ],
[-0.74080074, -0.36466932],
[ 0.6516018 , 0.9391426 ]],
[[ 1.038303 , 0.12231752],
[-0.94788766, -1.204232 ],
[ 4.059758 , 3.035752 ]],
[[ 0.56903946, -0.06875849],
[-0.35127294, 0.5311631 ],
[ 3.4635801 , 4.565582 ]],
[[-0.15989424, -0.25715637],
[ 0.87479895, 0.97391707],
[ 0.5211419 , 2.32108 ]]], dtype=float32)>
चूंकि batch_shape = (3,) और event_shape = (2,) , हम आकार का एक टेन्सर पारित (3, 2) को log_prob :
nd_batch.log_prob([[0., 0.], [1., 1.], [2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.8328519, -1.7907217, -1.694036 ], dtype=float32)>
प्रसारण, उर्फ यह इतना भ्रमित करने वाला क्यों है?
हम अब तक क्या किया है बाहर सार संक्षेप, हर वितरण एक बैच आकार B और एक घटना आकार E । आज्ञा देना BE घटना आकृतियों के संयोजन होना:
- Univariate अदिश वितरणों के लिए
nऔरb,BE = ().. - दो आयामी मल्टीवेरिएट normals के लिए
nd।BE = (2). - दोनों के लिए
b3औरb3_joint,BE = (3). - मल्टीवेरिएट normals के बैच के लिए
ndb,BE = (3, 2).
हम अब तक जिन "मूल्यांकन नियमों" का उपयोग कर रहे हैं वे हैं:
- कोई तर्क के साथ नमूना आकार के साथ एक टेन्सर रिटर्न
BE; एक अदिश n रिटर्न एक "द्वारा n के साथ नमूनाBE" टेन्सर। -
probऔरlog_probआकार का एक टेन्सर लेBEऔर आकार का एक परिणाम के लौटनेB।
के लिए वास्तविक "मूल्यांकन नियम" prob और log_prob अधिक जटिल है, एक तरह से है कि प्रस्तावों संभावित शक्ति और गति, लेकिन यह भी जटिलता और चुनौतियों। वास्तविक नियम (अनिवार्य) है कि करने के लिए तर्क है log_prob होना चाहिए broadcastable के खिलाफ BE ; आउटपुट में कोई भी "अतिरिक्त" आयाम संरक्षित हैं।
आइए निहितार्थों का पता लगाएं। Univariate सामान्य के लिए n , BE = () , तो log_prob एक अदिश की उम्मीद है। हम पार कर लेते हैं log_prob गैर खाली आकार के साथ एक टेन्सर, उन उत्पादन में बैच आयाम के रूप में दिखाई देते हैं:
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
n.log_prob([0.])
<tf.Tensor: shape=(1,), dtype=float32, numpy=array([-0.9189385], dtype=float32)>
n.log_prob([[0., 1.], [-1., 2.]])
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[-0.9189385, -1.4189385],
[-1.4189385, -2.9189386]], dtype=float32)>
आइए दो आयामी मल्टीवेरिएट सामान्य करने के लिए बारी nd (पैरामीटर निदर्शी प्रयोजनों के लिए बदल):
nd = tfd.MultivariateNormalDiag(loc=[0., 1.], scale_diag=[1., 1.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
log_prob "उम्मीद" आकार के साथ एक बहस (2,) , लेकिन यह किसी भी तर्क को स्वीकार करेंगे कि इस आकार के खिलाफ प्रसारण:
nd.log_prob([0., 0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
लेकिन हम "अधिक" उदाहरण में पारित कर सकते हैं, और उनके सब का मूल्यांकन log_prob 'एक ही बार में है:
nd.log_prob([[0., 0.],
[1., 1.],
[2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
शायद कम आकर्षक रूप से, हम घटना आयामों पर प्रसारित कर सकते हैं:
nd.log_prob([0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
nd.log_prob([[0.], [1.], [2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
इस तरह से प्रसारण करना हमारे "जब भी संभव हो प्रसारण सक्षम करें" डिजाइन का परिणाम है; यह उपयोग कुछ विवादास्पद है और संभावित रूप से TFP के भविष्य के संस्करण में इसे हटाया जा सकता है।
आइए अब तीन सिक्कों के उदाहरण को फिर से देखें:
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
इधर, प्रसारण का उपयोग कर संभावना प्रतिनिधित्व करने के लिए कि प्रत्येक सिक्का सिर ऊपर आता है काफी सहज है:
b3.prob([1])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.7 ], dtype=float32)>
(करने के लिए इस की तुलना करें b3.prob([1., 1., 1.]) है, जो हम इस्तेमाल किया वापस जहां होता b3 पेश किया गया था।)
अब मान लीजिए कि हम जानना चाहते हैं, प्रत्येक सिक्का के लिए, संभावना सिक्का ऊपर सिर आता है और संभावना यह पूंछ ऊपर आता है। हम कोशिश करने की कल्पना कर सकते हैं:
b3.log_prob([0, 1])
दुर्भाग्य से, यह एक लंबे और बहुत-पढ़ने योग्य स्टैक ट्रेस के साथ एक त्रुटि उत्पन्न करता है। b3 है BE = (3) तो हम से गुजरना होगा, b3.prob के खिलाफ कुछ broadcastable (3,) । [0, 1] आकार (2) , तो यह प्रसारित नहीं करता है और एक त्रुटि पैदा करता है। इसके बजाय, हमें कहना होगा:
b3.prob([[0], [1]])
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[0.7, 0.5, 0.3],
[0.3, 0.5, 0.7]], dtype=float32)>
क्यों? [[0], [1]] आकार (2, 1) , तो यह आकार के खिलाफ प्रसारण (3) के एक प्रसारण आकार बनाने के लिए (2, 3) ।
प्रसारण काफी शक्तिशाली है: ऐसे मामले हैं जहां यह उपयोग की जाने वाली स्मृति की मात्रा में परिमाण में कमी की अनुमति देता है, और यह अक्सर उपयोगकर्ता कोड को छोटा बनाता है। हालांकि, इसके साथ प्रोग्राम करना चुनौतीपूर्ण हो सकता है। यदि आप फोन log_prob और कोई त्रुटि मिलती है, प्रसारण के लिए एक विफलता लगभग हमेशा समस्या है।
आगे जाना
इस ट्यूटोरियल में, हमने (उम्मीद है) एक सरल परिचय प्रदान किया है। आगे जाने के लिए कुछ संकेत:
-
event_shape,batch_shapeऔरsample_shapeमनमाना रैंक हो सकता है (इस ट्यूटोरियल में वे हमेशा या तो अदिश या रैंक 1 कर रहे हैं)। यह शक्ति बढ़ाता है लेकिन फिर से प्रोग्रामिंग चुनौतियों का कारण बन सकता है, खासकर जब प्रसारण शामिल हो। आकार हेरफेर में एक अतिरिक्त गहरा गोता के लिए, देखें समझना TensorFlow वितरण आकृतियाँ । - TFP एक शक्तिशाली रूप में जाना जाता अमूर्त शामिल
Bijectors, जिसके साथ संयोजन के रूप मेंTransformedDistribution, आसानी से नए वितरण कि मौजूदा वितरण के उलटी परिवर्तनों हैं बनाने के लिए एक लचीला, compositional तरह से अर्जित करता है। हम इस पर जल्द ही एक ट्यूटोरियल लिखने की कोशिश करता हूँ, लेकिन इस बीच में, बाहर की जाँच प्रलेखन
