 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Delapan sekolah Masalah ( Rubin 1981 ) menganggap efektivitas program pembinaan SAT dilakukan secara paralel di delapan sekolah. Hal ini telah menjadi masalah klasik ( Bayesian Analisis Data , Stan ) yang menggambarkan kegunaan pemodelan hirarki untuk berbagi informasi antara kelompok ditukar.
Diimplementasikan di bawah ini adalah adaptasi dari sebuah Edward 1.0 tutorial .
Impor
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
import warnings
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
Data
Dari Analisis Data Bayesian, bagian 5.5 (Gelman et al. 2013):
Sebuah studi dilakukan untuk Educational Testing Service untuk menganalisis pengaruh program pembinaan khusus untuk SAT-V (Scholastic Aptitude Test-Verbal) di masing-masing dari delapan sekolah menengah. Variabel hasil dalam setiap penelitian adalah skor pada administrasi khusus SAT-V, tes pilihan ganda standar yang dikelola oleh Educational Testing Service dan digunakan untuk membantu perguruan tinggi membuat keputusan penerimaan; skor dapat bervariasi antara 200 dan 800, dengan rata-rata sekitar 500 dan standar deviasi sekitar 100. Ujian SAT dirancang agar tahan terhadap upaya jangka pendek yang diarahkan secara khusus untuk meningkatkan kinerja ujian; sebaliknya mereka dirancang untuk mencerminkan pengetahuan yang diperoleh dan kemampuan yang dikembangkan selama bertahun-tahun pendidikan. Namun demikian, masing-masing dari delapan sekolah dalam penelitian ini menilai program pembinaan jangka pendeknya sangat berhasil meningkatkan nilai SAT. Juga, tidak ada alasan sebelumnya untuk percaya bahwa salah satu dari delapan program lebih efektif daripada yang lain atau bahwa beberapa memiliki efek yang lebih mirip satu sama lain daripada yang lain.
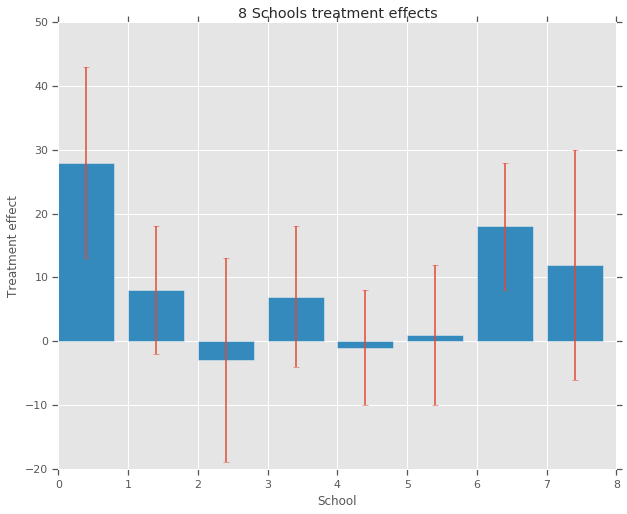
Untuk masing-masing dari delapan sekolah (\(J = 8\)), kita memiliki sekitar efek pengobatan \(y_j\) dan standard error dari efek estimasi \(\sigma_j\). Pengaruh perlakuan dalam penelitian ini diperoleh dengan regresi linier pada kelompok perlakuan dengan menggunakan skor PSAT-M dan PSAT-V sebagai variabel kontrol. Karena tidak ada kepercayaan sebelumnya bahwa salah satu sekolah yang kurang lebih mirip atau salah satu program pembinaan akan lebih efektif, kita bisa mempertimbangkan efek pengobatan sebagai tukar .
num_schools = 8 # number of schools
treatment_effects = np.array(
[28, 8, -3, 7, -1, 1, 18, 12], dtype=np.float32) # treatment effects
treatment_stddevs = np.array(
[15, 10, 16, 11, 9, 11, 10, 18], dtype=np.float32) # treatment SE
fig, ax = plt.subplots()
plt.bar(range(num_schools), treatment_effects, yerr=treatment_stddevs)
plt.title("8 Schools treatment effects")
plt.xlabel("School")
plt.ylabel("Treatment effect")
fig.set_size_inches(10, 8)
plt.show()
Model
Untuk menangkap data, kami menggunakan model normal hierarkis. Ini mengikuti proses generatif,
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i \sim \text{Normal}\left(\text{loc}{=}\mu,\ \text{scale}{=}\tau \right) \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
di mana \(\mu\) mewakili sebelum efek pengobatan rata-rata dan \(\tau\) kontrol berapa banyak varians ada antara sekolah. The \(y_i\) dan \(\sigma_i\) yang diamati. Sebagai \(\tau \rightarrow \infty\), model pendekatan model no-pooling, yaitu, masing-masing dari perkiraan efek pengobatan sekolah diperbolehkan untuk lebih mandiri. Sebagai \(\tau \rightarrow 0\), model pendekatan model lengkap-pooling, yaitu, semua efek pengobatan sekolah lebih dekat dengan kelompok rata-rata \(\mu\). Untuk membatasi standar deviasi positif, kita menarik \(\tau\) dari distribusi lognormal (yang setara dengan menggambar \(log(\tau)\) dari distribusi normal).
Berikut Mendiagnosis Bias Inference dengan Divergensi , kita mengubah model di atas menjadi setara model non-berpusat:
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i' \sim \text{Normal}\left(\text{loc}{=}0,\ \text{scale}{=}1 \right) \\ & \theta_i = \mu + \tau \theta_i' \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
Kami reify model ini sebagai JointDistributionSequential contoh:
model = tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=10., name="avg_effect"), # `mu` above
tfd.Normal(loc=5., scale=1., name="avg_stddev"), # `log(tau)` above
tfd.Independent(tfd.Normal(loc=tf.zeros(num_schools),
scale=tf.ones(num_schools),
name="school_effects_standard"), # `theta_prime`
reinterpreted_batch_ndims=1),
lambda school_effects_standard, avg_stddev, avg_effect: (
tfd.Independent(tfd.Normal(loc=(avg_effect[..., tf.newaxis] +
tf.exp(avg_stddev[..., tf.newaxis]) *
school_effects_standard), # `theta` above
scale=treatment_stddevs),
name="treatment_effects", # `y` above
reinterpreted_batch_ndims=1))
])
def target_log_prob_fn(avg_effect, avg_stddev, school_effects_standard):
"""Unnormalized target density as a function of states."""
return model.log_prob((
avg_effect, avg_stddev, school_effects_standard, treatment_effects))
Inferensi Bayesian
Data yang diberikan, kami melakukan Hamiltonian Monte Carlo (HMC) untuk menghitung distribusi posterior di atas parameter model.
num_results = 5000
num_burnin_steps = 3000
# Improve performance by tracing the sampler using `tf.function`
# and compiling it using XLA.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
tf.zeros([], name='init_avg_effect'),
tf.zeros([], name='init_avg_stddev'),
tf.ones([num_schools], name='init_school_effects_standard'),
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.4,
num_leapfrog_steps=3))
states, kernel_results = do_sampling()
avg_effect, avg_stddev, school_effects_standard = states
school_effects_samples = (
avg_effect[:, np.newaxis] +
np.exp(avg_stddev)[:, np.newaxis] * school_effects_standard)
num_accepted = np.sum(kernel_results.is_accepted)
print('Acceptance rate: {}'.format(num_accepted / num_results))
Acceptance rate: 0.5974
fig, axes = plt.subplots(8, 2, sharex='col', sharey='col')
fig.set_size_inches(12, 10)
for i in range(num_schools):
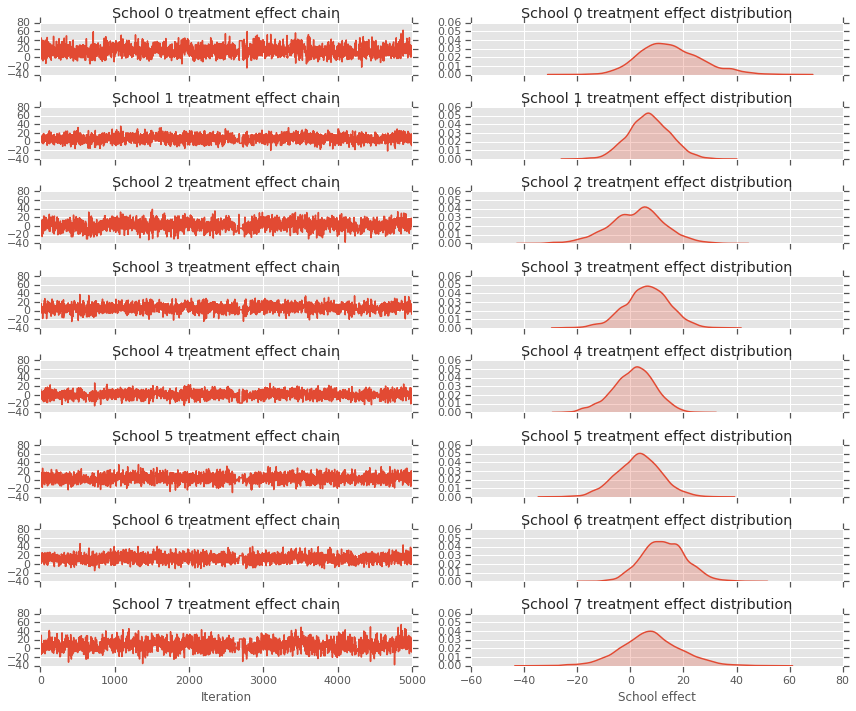
axes[i][0].plot(school_effects_samples[:,i].numpy())
axes[i][0].title.set_text("School {} treatment effect chain".format(i))
sns.kdeplot(school_effects_samples[:,i].numpy(), ax=axes[i][1], shade=True)
axes[i][1].title.set_text("School {} treatment effect distribution".format(i))
axes[num_schools - 1][0].set_xlabel("Iteration")
axes[num_schools - 1][1].set_xlabel("School effect")
fig.tight_layout()
plt.show()
print("E[avg_effect] = {}".format(np.mean(avg_effect)))
print("E[avg_stddev] = {}".format(np.mean(avg_stddev)))
print("E[school_effects_standard] =")
print(np.mean(school_effects_standard[:, ]))
print("E[school_effects] =")
print(np.mean(school_effects_samples[:, ], axis=0))
E[avg_effect] = 5.57183933258 E[avg_stddev] = 2.47738981247 E[school_effects_standard] = 0.08509017 E[school_effects] = [15.0051 7.103311 2.4552586 6.2744603 1.3364682 3.1125953 12.762501 7.743602 ]
# Compute the 95% interval for school_effects
school_effects_low = np.array([
np.percentile(school_effects_samples[:, i], 2.5) for i in range(num_schools)
])
school_effects_med = np.array([
np.percentile(school_effects_samples[:, i], 50) for i in range(num_schools)
])
school_effects_hi = np.array([
np.percentile(school_effects_samples[:, i], 97.5)
for i in range(num_schools)
])
fig, ax = plt.subplots(nrows=1, ncols=1, sharex=True)
ax.scatter(np.array(range(num_schools)), school_effects_med, color='red', s=60)
ax.scatter(
np.array(range(num_schools)) + 0.1, treatment_effects, color='blue', s=60)
plt.plot([-0.2, 7.4], [np.mean(avg_effect),
np.mean(avg_effect)], 'k', linestyle='--')
ax.errorbar(
np.array(range(8)),
school_effects_med,
yerr=[
school_effects_med - school_effects_low,
school_effects_hi - school_effects_med
],
fmt='none')
ax.legend(('avg_effect', 'HMC', 'Observed effect'), fontsize=14)
plt.xlabel('School')
plt.ylabel('Treatment effect')
plt.title('HMC estimated school treatment effects vs. observed data')
fig.set_size_inches(10, 8)
plt.show()
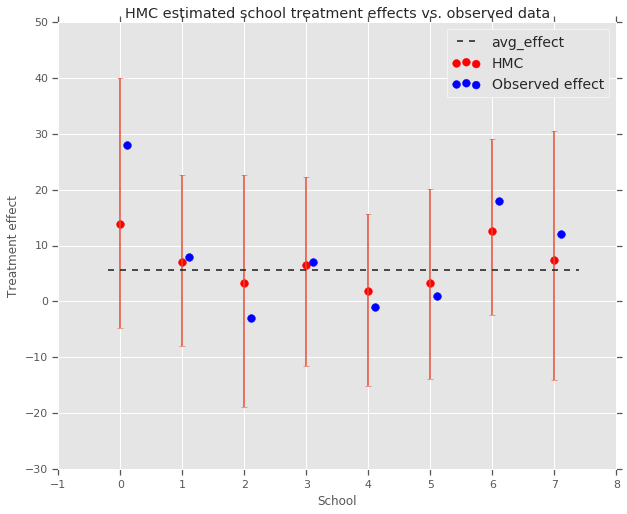
Kita bisa mengamati penyusutan terhadap kelompok avg_effect di atas.
print("Inferred posterior mean: {0:.2f}".format(
np.mean(school_effects_samples[:,])))
print("Inferred posterior mean se: {0:.2f}".format(
np.std(school_effects_samples[:,])))
Inferred posterior mean: 6.97 Inferred posterior mean se: 10.41
Kritik
Untuk mendapatkan distribusi prediksi posterior, yaitu, model data baru \(y^*\) diberi diamati Data \(y\):
\[ p(y^*|y) \propto \int_\theta p(y^* | \theta)p(\theta |y)d\theta\]
kita menimpa nilai dari variabel-variabel acak dalam model untuk mengatur mereka untuk mean dari distribusi posterior, dan sampel dari model yang menghasilkan data baru \(y^*\).
sample_shape = [5000]
_, _, _, predictive_treatment_effects = model.sample(
value=(tf.broadcast_to(np.mean(avg_effect, 0), sample_shape),
tf.broadcast_to(np.mean(avg_stddev, 0), sample_shape),
tf.broadcast_to(np.mean(school_effects_standard, 0),
sample_shape + [num_schools]),
None))
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(predictive_treatment_effects[:, 2*i].numpy(),
ax=ax[0], shade=True)
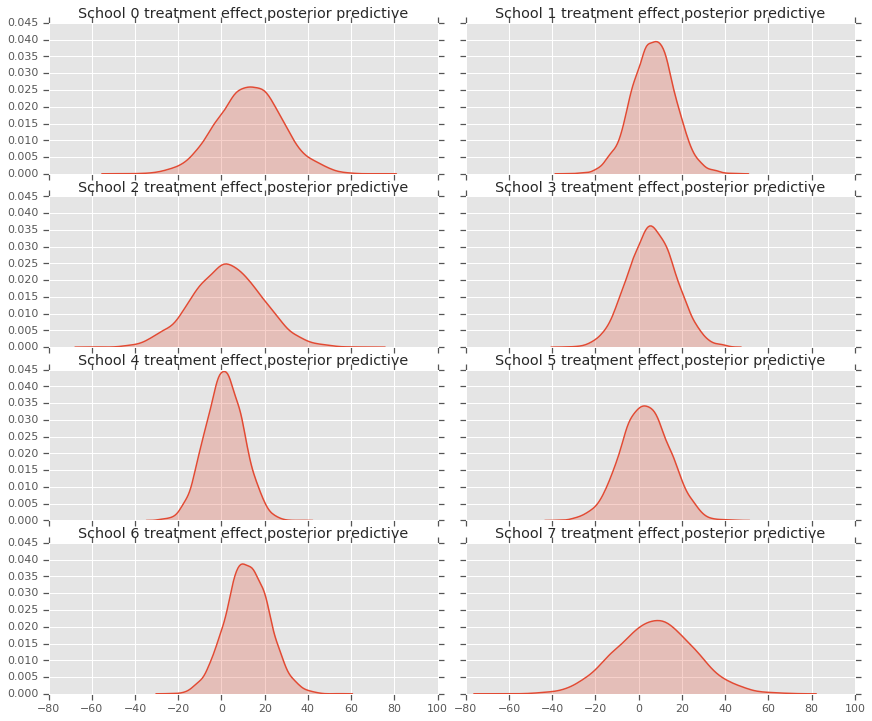
ax[0].title.set_text(
"School {} treatment effect posterior predictive".format(2*i))
sns.kdeplot(predictive_treatment_effects[:, 2*i + 1].numpy(),
ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect posterior predictive".format(2*i + 1))
plt.show()
# The mean predicted treatment effects for each of the eight schools.
prediction = np.mean(predictive_treatment_effects, axis=0)
Kita dapat melihat residual antara data efek perlakuan dan prediksi model posterior. Hal ini sesuai dengan plot di atas yang menunjukkan penyusutan efek yang diperkirakan terhadap rata-rata populasi.
treatment_effects - prediction
array([14.905351 , 1.2838383, -5.6966295, 0.8327627, -2.3356671,
-2.0363257, 5.997898 , 4.3731265], dtype=float32)
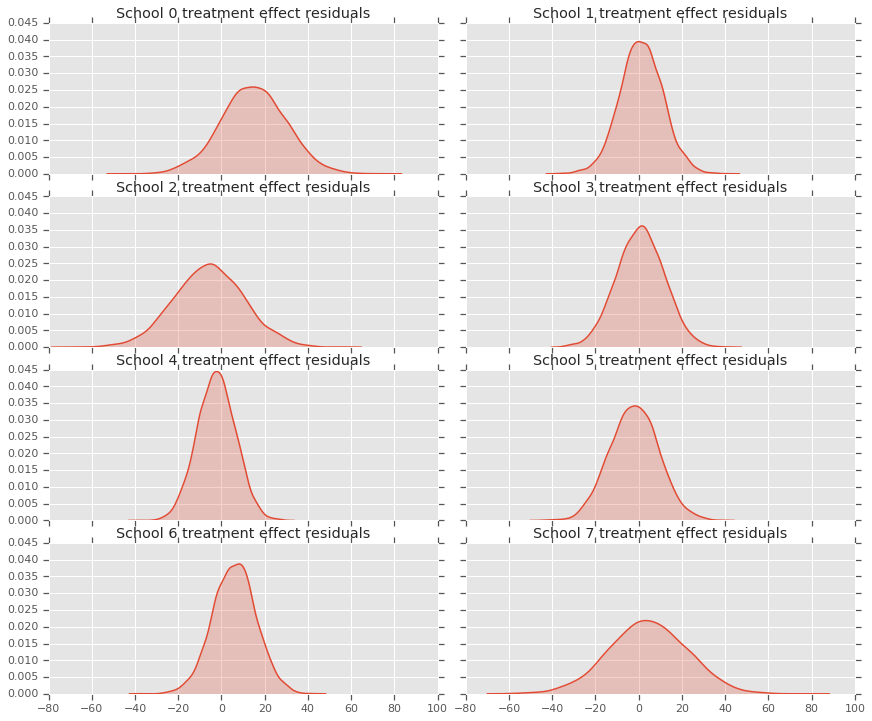
Karena kami memiliki distribusi prediksi untuk setiap sekolah, kami juga dapat mempertimbangkan distribusi residual.
residuals = treatment_effects - predictive_treatment_effects
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(residuals[:, 2*i].numpy(), ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect residuals".format(2*i))
sns.kdeplot(residuals[:, 2*i + 1].numpy(), ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect residuals".format(2*i + 1))
plt.show()
ucapan terima kasih
Tutorial ini awalnya ditulis dalam Edward 1.0 ( sumber ). Kami berterima kasih kepada semua kontributor untuk menulis dan merevisi versi itu.
Referensi
- Donald B. Rubin. Estimasi dalam percobaan acak paralel. Jurnal Statistik Pendidikan, 6(4):377-401, 1981.
- Andrew Gelman, John Carlin, Hal Stern, David Dunson, Aki Vehtari, and Donald Rubin. Analisis Data Bayesian, Edisi Ketiga. Chapman dan Hall/CRC, 2013.
