 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Sebuah model efek campuran linier adalah pendekatan sederhana untuk pemodelan hubungan linier terstruktur (Harville, 1997; Laird dan Ware, 1982). Setiap titik data terdiri dari input dari berbagai jenis—dikategorikan ke dalam kelompok—dan output bernilai nyata. Sebuah model efek campuran linear adalah model hirarkis: itu saham kekuatan statistik di seluruh kelompok dalam rangka meningkatkan kesimpulan tentang setiap titik data individu.
Dalam tutorial ini, kami mendemonstrasikan model efek campuran linier dengan contoh nyata di TensorFlow Probability. Kami akan menggunakan JointDistributionCoroutine dan Markov Chain Monte Carlo ( tfp.mcmc ) modul.
Dependensi & Prasyarat
Impor dan set up
import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')
Membuat hal-hal Cepat!
Sebelum kita masuk, pastikan kita menggunakan GPU untuk demo ini.
Untuk melakukan ini, pilih "Runtime" -> "Ubah jenis runtime" -> "Akselerator perangkat keras" -> "GPU".
Cuplikan berikut akan memverifikasi bahwa kami memiliki akses ke GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
Data
Kami menggunakan InstEval kumpulan data dari populer lme4 paket di R (Bates et al., 2015). Ini adalah kumpulan data kursus dan peringkat evaluasinya. Masing-masing tentu saja termasuk metadata seperti students , instructors , dan departments , dan variabel respon yang menarik adalah rating evaluasi.
def load_insteval():
"""Loads the InstEval data set.
It contains 73,421 university lecture evaluations by students at ETH
Zurich with a total of 2,972 students, 2,160 professors and
lecturers, and several student, lecture, and lecturer attributes.
Implementation is built from the `observations` Python package.
Returns:
Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
dictionary `metadata` of column headers (feature names).
"""
url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
'lme4/InstEval.csv')
with requests.Session() as s:
download = s.get(url)
f = download.content.decode().splitlines()
iterator = csv.reader(f)
columns = next(iterator)[1:]
x_train = np.array([row[1:] for row in iterator], dtype=np.int)
metadata = {'columns': columns}
return x_train, metadata
Kami memuat dan memproses kumpulan data sebelumnya. Kami menyimpan 20% dari data sehingga kami dapat mengevaluasi model yang dipasang pada titik data yang tidak terlihat. Di bawah ini kami memvisualisasikan beberapa baris pertama.
data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
'd': 'instructors',
'dept': 'departments',
'y': 'ratings'})
data['students'] -= 1 # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes
train = data.sample(frac=0.8)
test = data.drop(train.index)
train.head()
Kami mendirikan kumpulan data dalam hal features kamus input dan labels output yang sesuai dengan peringkat. Setiap fitur dikodekan sebagai bilangan bulat dan setiap label (peringkat evaluasi) dikodekan sebagai angka floating point.
get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
k: get_value(train, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)
features_test = {k: get_value(test, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)
num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]
print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)
Number of students: 2972 Number of instructors: 1128 Number of departments: 14 Number of observations: 58737
Model
Model linier tipikal mengasumsikan independensi, di mana setiap pasangan titik data memiliki hubungan linier yang konstan. Dalam InstEval set data, pengamatan timbul dalam kelompok yang masing-masing dapat memiliki berbagai lereng dan penyadapan. Model efek campuran linier, juga dikenal sebagai model linier hierarkis atau model linier bertingkat, menangkap fenomena ini (Gelman & Hill, 2006).
Contoh fenomena ini antara lain:
- Siswa. Pengamatan dari seorang siswa tidak independen: beberapa siswa mungkin secara sistematis memberikan peringkat kuliah yang rendah (atau tinggi).
- Instruktur. Pengamatan dari seorang instruktur tidak independen: kami mengharapkan guru yang baik umumnya memiliki peringkat yang baik dan guru yang buruk umumnya memiliki peringkat yang buruk.
- Departemen. Pengamatan dari sebuah departemen tidak independen: departemen tertentu mungkin umumnya memiliki bahan kering atau penilaian yang lebih ketat dan dengan demikian dinilai lebih rendah daripada yang lain.
Untuk menangkap ini, mengingat bahwa untuk satu set data \(N\times D\) fitur \(\mathbf{X}\) dan \(N\) label \(\mathbf{y}\), berpendapat regresi linear model
\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]
di mana ada vektor lereng \(\beta\in\mathbb{R}^D\), mencegat \(\alpha\in\mathbb{R}\), dan gangguan acak \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Kami mengatakan bahwa \(\beta\) dan \(\alpha\) adalah "efek tetap": mereka adalah efek tetap konstan di seluruh populasi titik data \((x, y)\). Formulasi setara dengan persamaan sebagai kemungkinan adalah \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\). Kemungkinan ini dimaksimalkan selama inferensi untuk menemukan perkiraan titik \(\beta\) dan \(\alpha\) yang sesuai dengan data.
Model efek campuran linier memperluas regresi linier sebagai
\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]
di mana masih ada vektor lereng \(\beta\in\mathbb{R}^P\), mencegat \(\alpha\in\mathbb{R}\), dan gangguan acak \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). Selain itu, ada istilah \(\mathbf{Z}\eta\), di mana \(\mathbf{Z}\) adalah fitur matriks dan \(\eta\in\mathbb{R}^Q\) adalah vektor dari lereng acak; \(\eta\) terdistribusi normal dengan parameter komponen varians \(\sigma^2\). \(\mathbf{Z}\) dibentuk oleh partisi asli \(N\times D\) fitur matriks dalam hal baru \(N\times P\) matriks \(\mathbf{X}\) dan \(N\times Q\) matriks \(\mathbf{Z}\), di mana \(P + Q=D\): partisi ini memungkinkan kita untuk model fitur secara terpisah menggunakan efek tetap \(\beta\) dan variabel laten \(\eta\) masing-masing.
Kita mengatakan variabel laten \(\eta\) adalah "efek acak": mereka adalah efek yang berbeda-beda di populasi (meskipun mereka mungkin konstan di sub-populasi). Secara khusus, karena efek random \(\eta\) memiliki mean 0, berarti label Data ini ditangkap oleh \(\mathbf{X}\beta + \alpha\). Efek acak komponen \(\mathbf{Z}\eta\) menangkap variasi dalam data: "Instruktur # 54 berperingkat 1,4 poin lebih tinggi daripada rata-rata" misalnya,
Dalam tutorial ini, kami menempatkan efek berikut:
- Efek tetap:
service.serviceadalah kovariat biner apakah kursus milik departemen utama instruktur. Tidak peduli berapa banyak data tambahan yang kami kumpulkan, hanya dapat mengambil nilai-nilai \(0\) dan \(1\). - Efek acak:
students,instructors, dandepartments. Mengingat lebih banyak pengamatan dari populasi penilaian evaluasi kursus, kita mungkin melihat siswa baru, guru, atau departemen.
Dalam sintaks paket lme4 R (Bates et al., 2015), model dapat diringkas sebagai
ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1
di mana x menunjukkan efek tetap, (1|x) menunjukkan efek acak untuk x , dan 1 menunjukkan istilah intercept.
Kami menerapkan model ini di bawah ini sebagai JointDistribution. Untuk memiliki dukungan yang lebih baik untuk pelacakan parameter (misalnya, kita ingin melacak semua tf.Variable di model.trainable_variables ), kami menerapkan template Model sebagai tf.Module .
class LinearMixedEffectModel(tf.Module):
def __init__(self):
# Set up fixed effects and other parameters.
# These are free parameters to be optimized in E-steps
self._intercept = tf.Variable(0., name="intercept") # alpha in eq
self._effect_service = tf.Variable(0., name="effect_service") # beta in eq
self._stddev_students = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_students") # sigma in eq
self._stddev_instructors = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_instructors") # sigma in eq
self._stddev_departments = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_departments") # sigma in eq
def __call__(self, features):
model = tfd.JointDistributionSequential([
# Set up random effects.
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_students),
scale_identity_multiplier=self._stddev_students),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_instructors),
scale_identity_multiplier=self._stddev_instructors),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_departments),
scale_identity_multiplier=self._stddev_departments),
# This is the likelihood for the observed.
lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
tfd.Normal(
loc=(self._effect_service * features["service"] +
tf.gather(effect_students, features["students"], axis=-1) +
tf.gather(effect_instructors, features["instructors"], axis=-1) +
tf.gather(effect_departments, features["departments"], axis=-1) +
self._intercept),
scale=1.),
reinterpreted_batch_ndims=1)
])
# To enable tracking of the trainable variables via the created distribution,
# we attach a reference to `self`. Since all TFP objects sub-class
# `tf.Module`, this means that the following is possible:
# LinearMixedEffectModel()(features_train).trainable_variables
# ==> tuple of all tf.Variables created by LinearMixedEffectModel.
model._to_track = self
return model
lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)
lmm_train.trainable_variables
(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)
Sebagai program grafis Probabilistik, kita juga dapat memvisualisasikan struktur model dalam bentuk grafik komputasinya. Grafik ini mengkodekan aliran data di seluruh variabel acak dalam program, membuat eksplisit hubungan mereka dalam hal model grafis (Jordan, 2003).
Sebagai alat statistik, kita mungkin melihat grafik dalam rangka untuk lebih melihat, misalnya, bahwa intercept dan effect_service yang kondisional tergantung diberikan ratings ; ini mungkin lebih sulit dilihat dari kode sumber jika program ditulis dengan kelas, referensi silang antar modul, dan/atau subrutin. Sebagai alat komputasi, kami juga mungkin melihat variabel laten mengalir ke ratings variabel melalui tf.gather ops. Hal ini mungkin menjadi hambatan pada akselerator hardware tertentu jika pengindeksan Tensor s mahal; memvisualisasikan grafik membuat ini mudah terlihat.
lmm_train.resolve_graph()
(('effect_students', ()),
('effect_instructors', ()),
('effect_departments', ()),
('x', ('effect_departments', 'effect_instructors', 'effect_students')))
Estimasi Parameter
Mengingat data, tujuan inferensi adalah agar sesuai dengan model efek tetap lereng \(\beta\), mencegat \(\alpha\), dan varians komponen parameter \(\sigma^2\). Prinsip kemungkinan maksimum memformalkan tugas ini sebagai:
\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]
Dalam tutorial ini, kami menggunakan algoritma Monte Carlo EM untuk memaksimalkan kepadatan marginal ini (Dempster et al., 1977; Wei dan Tanner, 1990).¹ Kami melakukan rantai Markov Monte Carlo untuk menghitung ekspektasi kemungkinan bersyarat sehubungan dengan efek acak ("Langkah E"), dan kami melakukan penurunan gradien untuk memaksimalkan ekspektasi sehubungan dengan parameter ("Langkah M"):
Untuk E-step, kami menyiapkan Hamiltonian Monte Carlo (HMC). Dibutuhkan status saat ini—efek siswa, instruktur, dan departemen—dan mengembalikan status baru. Kami menetapkan status baru ke variabel TensorFlow, yang akan menunjukkan status rantai HMC.
Untuk langkah-M, kami menggunakan sampel posterior dari HMC untuk menghitung perkiraan yang tidak bias dari kemungkinan marjinal hingga konstan. Kami kemudian menerapkan gradiennya sehubungan dengan parameter yang diinginkan. Ini menghasilkan langkah penurunan stokastik yang tidak bias pada kemungkinan marjinal. Kami menerapkannya dengan pengoptimal Adam TensorFlow dan meminimalkan negatif dari marginal.
target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]
# For debugging
target_log_prob_fn(*current_state)
<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>
# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.015,
num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)
@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
next_state, next_kernel_results = hmc.one_step(
current_state=current_state,
previous_kernel_results=kernel_results)
return next_state, next_kernel_results
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
with tf.GradientTape() as tape:
loss = -target_log_prob_fn(*current_state)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
Kami melakukan tahap pemanasan, yang menjalankan satu rantai MCMC untuk sejumlah iterasi sehingga pelatihan dapat diinisialisasi dalam massa probabilitas posterior. Kami kemudian menjalankan loop pelatihan. Ini bersama-sama menjalankan E dan M-langkah dan mencatat nilai selama pelatihan.
num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])
# Run warm-up stage.
for t in range(num_warmup_iters):
current_state, kernel_results = one_e_step(current_state, kernel_results)
num_accepted += kernel_results.is_accepted.numpy()
if t % 500 == 0 or t == num_warmup_iters - 1:
print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
t, num_accepted / (t + 1)))
num_accepted = 0 # reset acceptance rate counter
# Run training.
for t in range(num_iters):
# run 5 MCMC iterations before every joint EM update
for _ in range(5):
current_state, kernel_results = one_e_step(current_state, kernel_results)
loss = one_m_step(current_state)
effect_students_samples[t, :] = current_state[0].numpy()
effect_instructors_samples[t, :] = current_state[1].numpy()
effect_departments_samples[t, :] = current_state[2].numpy()
num_accepted += kernel_results.is_accepted.numpy()
loss_history[t] = loss.numpy()
if t % 500 == 0 or t == num_iters - 1:
print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
t, num_accepted / (t + 1), loss_history[t]))
Warm-Up Iteration: 0 Acceptance Rate: 1.000 Warm-Up Iteration: 500 Acceptance Rate: 0.754 Warm-Up Iteration: 999 Acceptance Rate: 0.707 Iteration: 0 Acceptance Rate: 1.000 Loss: 98220.266 Iteration: 500 Acceptance Rate: 0.703 Loss: 96003.969 Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609 Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891
Anda juga dapat menulis pemanasan untuk loop menjadi tf.while_loop , dan langkah pelatihan menjadi tf.scan atau tf.while_loop untuk lebih cepat inferensi. Sebagai contoh:
@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
_, next_state, next_kernel_results = tf.while_loop(
cond=lambda i, state, pkr: i < k,
body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
loop_vars=(tf.constant(0), current_state, kernel_results)
)
return next_state, next_kernel_results
Di atas, kami tidak menjalankan algoritme sampai ambang konvergensi terdeteksi. Untuk memeriksa apakah pelatihan masuk akal, kami memverifikasi bahwa fungsi kerugian memang cenderung menyatu pada iterasi pelatihan.
plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()
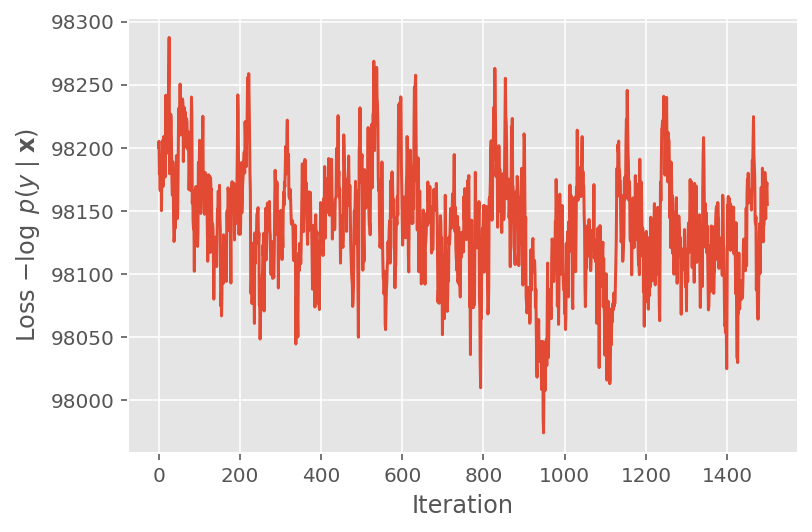
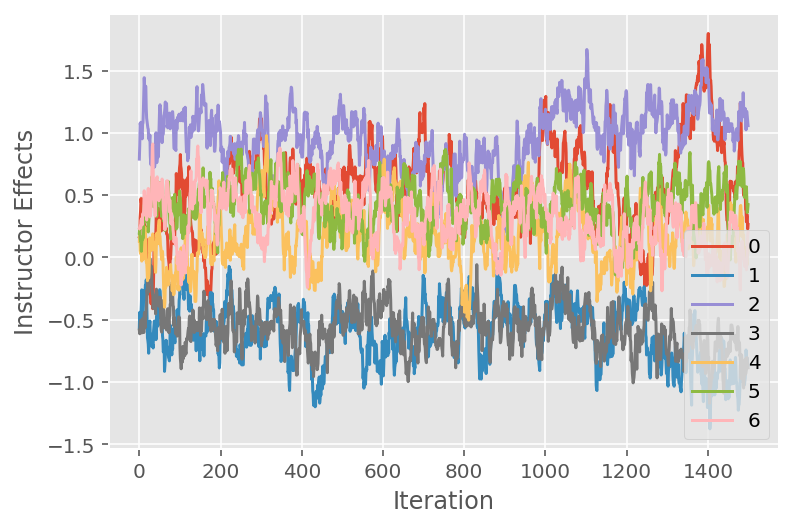
Kami juga menggunakan plot jejak, yang menunjukkan lintasan rantai Markov algoritma Monte Carlo melintasi dimensi laten tertentu. Di bawah ini kita melihat bahwa efek instruktur tertentu memang bertransisi secara bermakna dari keadaan awalnya dan menjelajahi ruang keadaan. Plot jejak juga menunjukkan bahwa efeknya berbeda antar instruktur tetapi dengan perilaku pencampuran yang serupa.
for i in range(7):
plt.plot(effect_instructors_samples[:, i])
plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()
Kritik
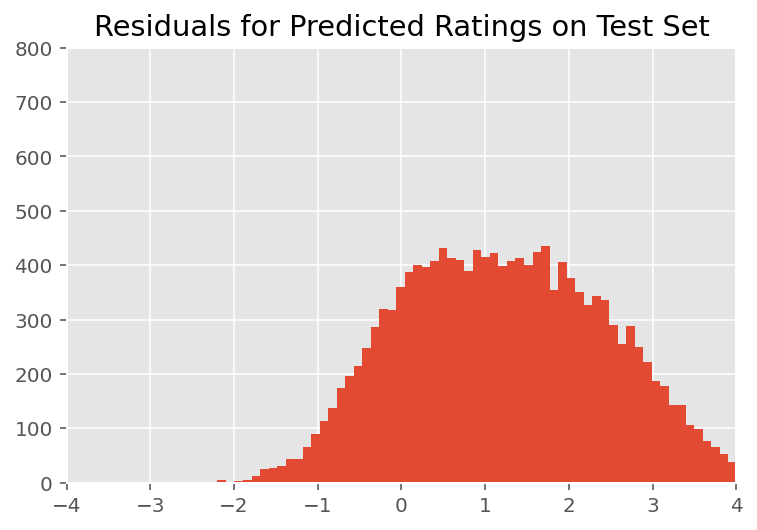
Di atas, kami memasang modelnya. Kami sekarang melihat ke dalam mengkritik kecocokannya menggunakan data, yang memungkinkan kami menjelajahi dan lebih memahami model. Salah satu teknik tersebut adalah plot residual, yang memplot perbedaan antara prediksi model dan kebenaran dasar untuk setiap titik data. Jika modelnya benar, maka perbedaannya harus terdistribusi normal standar; setiap penyimpangan dari pola ini dalam plot menunjukkan ketidakcocokan model.
Kami membangun plot residual dengan terlebih dahulu membentuk distribusi prediktif posterior di atas peringkat, yang menggantikan distribusi sebelumnya pada efek acak dengan data pelatihan yang diberikan posterior. Secara khusus, kami menjalankan model ke depan dan mencegat ketergantungannya pada efek acak sebelumnya dengan cara posterior yang disimpulkan.²
lmm_test = lmm_jointdist(features_test)
[
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
] = [
np.mean(x, axis=0).astype(np.float32) for x in [
effect_students_samples,
effect_instructors_samples,
effect_departments_samples
]
]
# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
value=(
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
))
ratings_prediction = ratings_posterior.mean()
Setelah inspeksi visual, residu terlihat agak standar-terdistribusi normal. Namun, kecocokannya tidak sempurna: ada massa probabilitas yang lebih besar di bagian ekor daripada distribusi normal, yang menunjukkan bahwa model dapat meningkatkan kecocokannya dengan melonggarkan asumsi normalitasnya.
Secara khusus, meskipun yang paling umum untuk menggunakan distribusi normal untuk peringkat model dalam InstEval kumpulan data, melihat lebih dekat pada data mengungkapkan bahwa peringkat evaluasi saja yang nilai ordinal sebenarnya dari 1 sampai 5. Hal ini menunjukkan bahwa kita harus menggunakan distribusi ordinal, atau bahkan Kategoris jika kita memiliki cukup data untuk membuang urutan relatif. Ini adalah perubahan satu baris ke model di atas; kode inferensi yang sama berlaku.
plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()
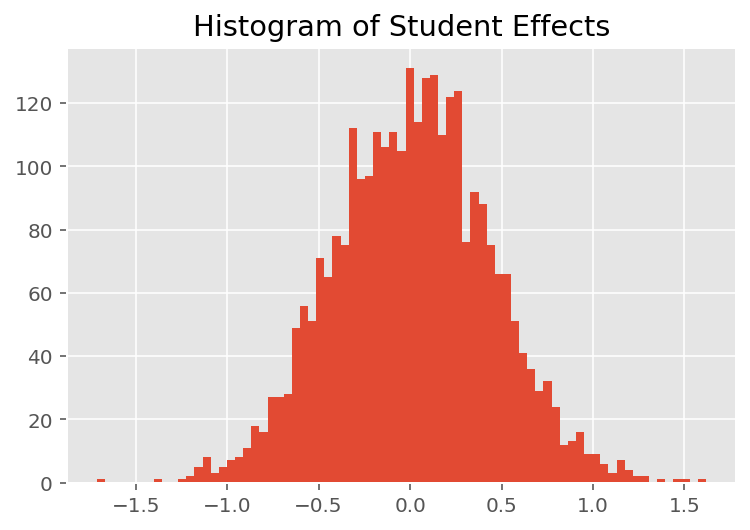
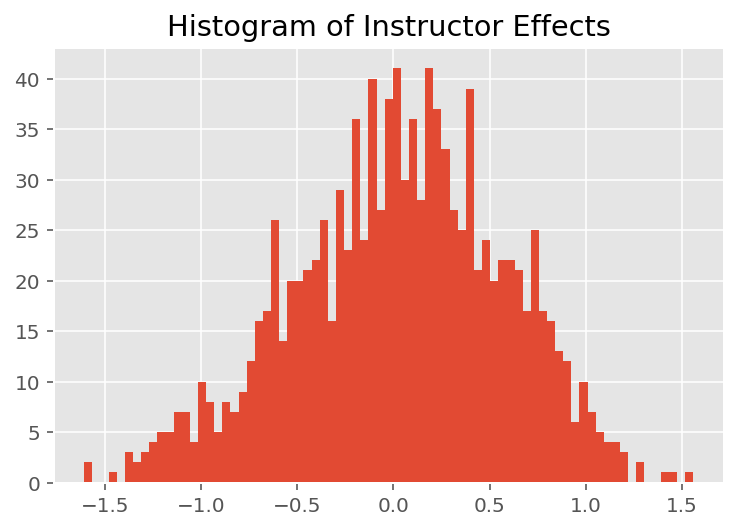
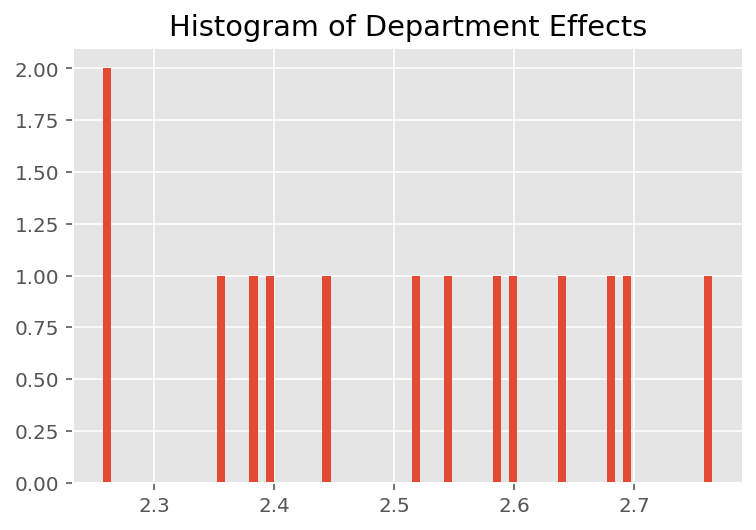
Untuk mengeksplorasi bagaimana model membuat prediksi individu, kita melihat histogram efek untuk siswa, instruktur, dan departemen. Ini memungkinkan kita memahami bagaimana elemen individual dalam vektor fitur titik data cenderung memengaruhi hasil.
Tidak mengherankan, kita melihat di bawah bahwa setiap siswa biasanya memiliki sedikit pengaruh pada penilaian evaluasi instruktur. Menariknya, kita melihat bahwa departemen yang dimiliki seorang instruktur memiliki pengaruh yang besar.
plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()
plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()
plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()
Catatan kaki
Model efek campuran linier adalah kasus khusus di mana kita dapat menghitung densitas marginalnya secara analitis. Untuk tujuan tutorial ini, kami mendemonstrasikan Monte Carlo EM, yang lebih siap diterapkan pada kepadatan marginal non-analitik seperti jika kemungkinan diperluas menjadi Kategorikal, bukan Normal.
² Untuk mempermudah, kami membentuk rata-rata distribusi prediktif dengan hanya menggunakan satu lintasan maju model. Hal ini dilakukan dengan pengkondisian pada mean posterior dan berlaku untuk model efek campuran linier. Namun, ini tidak berlaku secara umum: rata-rata distribusi prediktif posterior biasanya tidak dapat diselesaikan dan membutuhkan pengambilan rata-rata empiris di beberapa lintasan maju dari model yang diberikan sampel posterior.
ucapan terima kasih
Tutorial ini awalnya ditulis dalam Edward 1.0 ( sumber ). Kami berterima kasih kepada semua kontributor untuk menulis dan merevisi versi itu.
Referensi
Douglas Bates dan Martin Machler dan Ben Bolker dan Steve Walker. Memasang Model Efek Campuran Linear Menggunakan lme4. Jurnal statistik Software, 67 (1): 1-48, 2015.
Arthur P. Dempster, Nan M. Laird, dan Donald B. Rubin. Kemungkinan maksimum dari data yang tidak lengkap melalui algoritma EM. Jurnal Royal Society Statistik, Seri B (metodologis), 1-38, 1977.
Andrew Gelman dan Jennifer Hill. Analisis data menggunakan regresi dan model bertingkat/hierarki. Cambridge University Press, 2006.
David A.Harville. Pendekatan kemungkinan maksimum untuk estimasi komponen varians dan masalah terkait. Journal of American Association statistik, 72 (358): 320-338, 1977.
Michael I. Jordan. Pengantar Model Grafis. Laporan Teknis, 2003.
Nan M. Laird dan James Ware. Model efek acak untuk data longitudinal. Biometrics, 963-974, 1982.
Greg Wei dan Martin A. Tanner. Implementasi Monte Carlo dari algoritma EM dan algoritma augmentasi data orang miskin. Journal of American Association statistik, 699-704, 1990.
