TensorFlow.org에서 보기 TensorFlow.org에서 보기 |  Google Colab에서 실행 Google Colab에서 실행 |  GitHub에서 소스 보기 GitHub에서 소스 보기 |  노트북 다운로드 노트북 다운로드 |
이것은 Li et al.의 2020년 3월 16일 논문의 TensorFlow Probability 포트입니다. TensorFlow Probability 플랫폼에서 원저자의 방법과 결과를 충실하게 재현하여 현대 역학 모델링 환경에서 TFP의 일부 기능을 보여줍니다. TensorFlow로 포팅하면 원본 Matlab 코드에 비해 10배 더 빠른 속도를 얻을 수 있으며, TensorFlow Probability는 벡터화된 배치 계산을 광범위하게 지원하기 때문에 수백 개의 독립적인 복제로 유리하게 확장됩니다.
원본 용지
Ruiyun Li, Sen Pei, Bin Chen, Yimeng Song, Tao Zhang, Wan Yang, Jeffrey Shaman. 상당한 문서화되지 않은 감염은 신종 코로나바이러스(SARS-CoV2)의 빠른 전파를 촉진합니다. (2020), 도이 : https://doi.org/10.1126/science.abb3221 .
초록. "유병률 및 문서화되지 않은 새로운 코로나 바이러스 (SARS-CoV2) 감염의 전염성의 평가는 전체적인 유병률과이 질병의 대유행 가능성을 이해하는 데 중요하다 여기에서 우리는 모바일 데이터하는와 함께 중국 내에서보고 된 감염의 관찰을 사용 문서화되지 않은 감염의 비율 및 전염성을 포함하여 SARS-CoV2와 관련된 중요한 역학적 특성을 추론하기 위해 네트워크로 연결된 동적 메타인구 모델 및 베이지안 추론을 사용하여 모든 감염의 86%가 문서화되지 않은 것으로 추정합니다(95% CI: [82%–90%] ) 2020년 1월 23일 이전 여행 제한 1인당 문서화되지 않은 감염의 전파율은 문서화된 감염의 55%([46%–62%])였지만 더 많은 수로 인해 문서화되지 않은 감염이 79명의 감염원이었습니다. 문서화된 사례의 %. 이러한 발견은 SARS-CoV2의 급속한 지리적 확산을 설명하고 이 바이러스의 억제가 특히 어려울 것임을 나타냅니다."
Github의 링크 코드와 데이터.
개요
모델은이다 구획되지 질병 모델 "취약", "노출"(감염 아직 감염되지 않음), "전염성 문서화 결코"및 "전염성 결국 문서화"에 대한 구획 함께. 두 가지 주목할만한 특징이 있습니다. 사람들이 한 도시에서 다른 도시로 여행하는 방법에 대한 가정을 바탕으로 375개의 중국 도시 각각에 대해 별도의 구획이 있습니다. 그리고이되는 경우는 일의 "감염 결국 문서화"그래서 감염을보고 지연, \(t\) 확률 나중에 날까지 관찰 된 경우 카운트에 표시되지 않습니다.
이 모델은 문서화되지 않은 사례가 더 경미하여 문서화되지 않고 더 낮은 비율로 다른 사람들을 감염시킨다고 가정합니다. 원본 문서에서 주요 관심 매개변수는 문서화되지 않은 사례의 비율로, 기존 감염의 정도와 문서화되지 않은 전파가 질병의 확산에 미치는 영향을 모두 추정합니다.
이 colab은 상향식 코드 연습으로 구성되어 있습니다. 순서대로, 우리는
- 데이터를 수집하고 간략하게 검토하고,
- 모델의 상태 공간과 역학을 정의하고,
- Li et al을 따라 모델에서 추론을 수행하기 위한 함수 모음을 구축하고,
- 그들을 호출하고 결과를 조사하십시오. 스포일러: 종이와 같이 나옵니다.
설치 및 Python 가져오기
pip3 install -q tf-nightly tfp-nightly
import collections
import io
import requests
import time
import zipfile
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability.python.internal import samplers
tfd = tfp.distributions
tfes = tfp.experimental.sequential
데이터 가져오기
github에서 데이터를 가져와서 일부를 살펴보겠습니다.
r = requests.get('https://raw.githubusercontent.com/SenPei-CU/COVID-19/master/Data.zip')
z = zipfile.ZipFile(io.BytesIO(r.content))
z.extractall('/tmp/')
raw_incidence = pd.read_csv('/tmp/data/Incidence.csv')
raw_mobility = pd.read_csv('/tmp/data/Mobility.csv')
raw_population = pd.read_csv('/tmp/data/pop.csv')
아래에서 우리는 하루의 원시 발생 횟수를 볼 수 있습니다. 여행 제한이 23일부터 시행되었기 때문에 첫 14일(1월 10일~1월 23일)이 가장 궁금합니다. 이 논문은 1월 10-23일과 1월 23일 이상을 서로 다른 매개변수를 사용하여 별도로 모델링하여 이를 처리합니다. 우리는 재생산을 이전 기간으로 제한할 것입니다.
raw_incidence.drop('Date', axis=1) # The 'Date' column is all 1/18/21
# Luckily the days are in order, starting on January 10th, 2020.
우한 발병 건수 건전성 확인합시다.
plt.plot(raw_incidence.Wuhan, '.-')
plt.title('Wuhan incidence counts over 1/10/20 - 02/08/20')
plt.show()
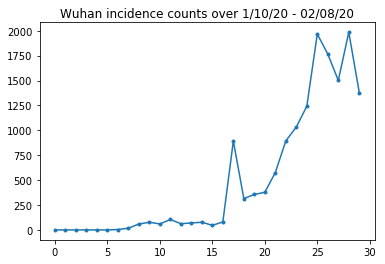
여태까지는 그런대로 잘됐다. 이제 초기 인구가 계산됩니다.
raw_population
어떤 입국이 우한인지도 확인하고 기록하자.
raw_population['City'][169]
'Wuhan'
WUHAN_IDX = 169
여기에서 서로 다른 도시 간의 이동성 매트릭스를 볼 수 있습니다. 이것은 처음 14일 동안 다른 도시 사이를 이동하는 사람들의 수에 대한 프록시입니다. Tencent가 2018년 설날 시즌에 제공한 GPS 기록에서 파생되었습니다. 알 수없는 (추론에 따라) 일정 요인으로 2020 년 시즌 동안 리튬 등 모델 이동성 \(\theta\) 시간이.
raw_mobility
마지막으로 이 모든 것을 우리가 사용할 수 있는 numpy 배열로 전처리해 보겠습니다.
# The given populations are only "initial" because of intercity mobility during
# the holiday season.
initial_population = raw_population['Population'].to_numpy().astype(np.float32)
이동성 데이터를 [L, L, T] 모양의 Tensor로 변환합니다. 여기서 L은 위치 수이고 T는 시간 단계 수입니다.
daily_mobility_matrices = []
for i in range(1, 15):
day_mobility = raw_mobility[raw_mobility['Day'] == i]
# Make a matrix of daily mobilities.
z = pd.crosstab(
day_mobility.Origin,
day_mobility.Destination,
values=day_mobility['Mobility Index'], aggfunc='sum', dropna=False)
# Include every city, even if there are no rows for some in the raw data on
# some day. This uses the sort order of `raw_population`.
z = z.reindex(index=raw_population['City'], columns=raw_population['City'],
fill_value=0)
# Finally, fill any missing entries with 0. This means no mobility.
z = z.fillna(0)
daily_mobility_matrices.append(z.to_numpy())
mobility_matrix_over_time = np.stack(daily_mobility_matrices, axis=-1).astype(
np.float32)
마지막으로 관찰된 감염을 취하여 [L, T] 테이블을 만듭니다.
# Remove the date parameter and take the first 14 days.
observed_daily_infectious_count = raw_incidence.to_numpy()[:14, 1:]
observed_daily_infectious_count = np.transpose(
observed_daily_infectious_count).astype(np.float32)
그리고 원하는 모양을 얻었는지 다시 확인하십시오. 참고로 우리는 14일 동안 375개 도시와 협력하고 있습니다.
print('Mobility Matrix over time should have shape (375, 375, 14): {}'.format(
mobility_matrix_over_time.shape))
print('Observed Infectious should have shape (375, 14): {}'.format(
observed_daily_infectious_count.shape))
print('Initial population should have shape (375): {}'.format(
initial_population.shape))
Mobility Matrix over time should have shape (375, 375, 14): (375, 375, 14) Observed Infectious should have shape (375, 14): (375, 14) Initial population should have shape (375): (375,)
상태 및 매개변수 정의
모델 정의를 시작하겠습니다. 우리가 재현되는 모델은의 변종이다 SEIR 모델 . 이 경우 다음과 같은 시변 상태가 있습니다.
- \(S\)각 도시에서 질병에 민감한 사람들의 수.
- \(E\): 질병에 노출 각 도시에있는 사람들의 수 있지만 전염성 아직. 생물학적으로 이것은 모든 노출된 사람들이 결국 감염된다는 점에서 질병에 걸리는 것과 같습니다.
- \(I^u\): 전염성하지만 문서화되어 각 도시에있는 사람들의 수. 모델에서 이것은 실제로 "절대 문서화되지 않을 것"을 의미합니다.
- \(I^r\): 감염과 같은 문서화되어 각 도시에있는 사람들의 수. 리튬 등 모델보고 지연, 그래서 \(I^r\) 실제로 "미래의 어떤 시점에서 문서화되어야 할 심각한 정도 인 경우"같은에 해당합니다.
아래에서 볼 수 있듯이 Ensemble-adjusted Kalman Filter(EAKF)를 앞으로 실행하여 이러한 상태를 유추할 것입니다. EAKF의 상태 벡터는 이러한 각 수량에 대해 하나의 도시 색인 벡터입니다.
모델에는 다음과 같은 추론 가능한 전역 시불변 매개변수가 있습니다.
- \(\beta\): 때문에 문서화 된 감염성 개인에 대한 전송 속도.
- \(\mu\): 때문에 문서화되지 않은 감염성 개인 상대 전송 속도. 이 제품을 통해 역할을 \(\mu \beta\).
- \(\theta\): 도시 간 이동성 요소. 이는 이동성 데이터의 과소 보고(2018년부터 2020년까지의 인구 증가)를 수정하는 데 1보다 큰 요소입니다.
- \(Z\): 평균 잠복기 (즉, "노출"상태 시간).
- \(\alpha\):이있을 정도로 심각한 감염의 비율이다 (결국) 기록.
- \(D\): 감염의 평균 지속 시간 (즉, 하나 "전염성"상태 시간).
상태에 대한 EAKF 주변의 반복 필터링 루프를 사용하여 이러한 매개변수에 대한 점 추정치를 추론할 것입니다.
모델은 추론되지 않은 상수에도 의존합니다.
- \(M\): 도시 간 이동 행렬. 이것은 시간에 따라 달라지며 주어진 것으로 추정됩니다. 이 추정 된 매개 변수에 의해 조정 있다고 리콜 \(\theta\) 도시 사이의 실제 인구 이동을 제공합니다.
- \(N\): 각 도시에있는 사람의 총 수입니다. 주어진 초기 인구를 가지고 있으며, 인구의 시간 변화는 이동성 번호에서 계산 \(\theta M\).
먼저 상태와 매개변수를 유지하기 위한 몇 가지 데이터 구조를 제공합니다.
SEIRComponents = collections.namedtuple(
typename='SEIRComponents',
field_names=[
'susceptible', # S
'exposed', # E
'documented_infectious', # I^r
'undocumented_infectious', # I^u
# This is the count of new cases in the "documented infectious" compartment.
# We need this because we will introduce a reporting delay, between a person
# entering I^r and showing up in the observable case count data.
# This can't be computed from the cumulative `documented_infectious` count,
# because some portion of that population will move to the 'recovered'
# state, which we aren't tracking explicitly.
'daily_new_documented_infectious'])
ModelParams = collections.namedtuple(
typename='ModelParams',
field_names=[
'documented_infectious_tx_rate', # Beta
'undocumented_infectious_tx_relative_rate', # Mu
'intercity_underreporting_factor', # Theta
'average_latency_period', # Z
'fraction_of_documented_infections', # Alpha
'average_infection_duration' # D
]
)
또한 매개변수 값에 대한 Li et al의 경계를 코딩합니다.
PARAMETER_LOWER_BOUNDS = ModelParams(
documented_infectious_tx_rate=0.8,
undocumented_infectious_tx_relative_rate=0.2,
intercity_underreporting_factor=1.,
average_latency_period=2.,
fraction_of_documented_infections=0.02,
average_infection_duration=2.
)
PARAMETER_UPPER_BOUNDS = ModelParams(
documented_infectious_tx_rate=1.5,
undocumented_infectious_tx_relative_rate=1.,
intercity_underreporting_factor=1.75,
average_latency_period=5.,
fraction_of_documented_infections=1.,
average_infection_duration=5.
)
SEIR 역학
여기에서 매개변수와 상태 간의 관계를 정의합니다.
Li et al(보충 자료, eqns 1-5)의 시간 역학 방정식은 다음과 같습니다.
\(\frac{dS_i}{dt} = -\beta \frac{S_i I_i^r}{N_i} - \mu \beta \frac{S_i I_i^u}{N_i} + \theta \sum_k \frac{M_{ij} S_j}{N_j - I_j^r} - + \theta \sum_k \frac{M_{ji} S_j}{N_i - I_i^r}\)
\(\frac{dE_i}{dt} = \beta \frac{S_i I_i^r}{N_i} + \mu \beta \frac{S_i I_i^u}{N_i} -\frac{E_i}{Z} + \theta \sum_k \frac{M_{ij} E_j}{N_j - I_j^r} - + \theta \sum_k \frac{M_{ji} E_j}{N_i - I_i^r}\)
\(\frac{dI^r_i}{dt} = \alpha \frac{E_i}{Z} - \frac{I_i^r}{D}\)
\(\frac{dI^u_i}{dt} = (1 - \alpha) \frac{E_i}{Z} - \frac{I_i^u}{D} + \theta \sum_k \frac{M_{ij} I_j^u}{N_j - I_j^r} - + \theta \sum_k \frac{M_{ji} I^u_j}{N_i - I_i^r}\)
\(N_i = N_i + \theta \sum_j M_{ij} - \theta \sum_j M_{ji}\)
미리 알림의로 \(i\) 및 \(j\) 첨자 인덱스 도시. 이 방정식은 다음을 통해 질병의 시간 경과를 모델링합니다.
- 더 많은 감염을 유발하는 전염성 개인과의 접촉;
- "노출" 상태에서 "전염성" 상태 중 하나로 질병 진행;
- "전염성" 상태에서 회복으로의 질병 진행, 우리는 모델링된 인구에서 제거하여 모델링합니다.
- 노출되거나 문서화되지 않은 감염자를 포함한 도시 간 이동 그리고
- 도시 간 이동을 통한 일일 도시 인구의 시간 변화.
Li et al에 따르면 우리는 결국 보고될 만큼 심각한 사례를 가진 사람들이 도시 사이를 여행하지 않는다고 가정합니다.
또한 Li et al에 따라 우리는 이러한 역학을 항별 푸아송 노이즈의 대상으로 취급합니다. 즉, 각 항은 실제로 실제 변화를 제공하는 샘플인 푸아송의 비율입니다. 푸아송 노이즈는 푸아송 샘플을 빼면(추가하는 것과 반대) 푸아송 분포 결과가 생성되지 않기 때문에 항에 따라 다릅니다.
고전적인 4차 Runge-Kutta 적분기를 사용하여 이러한 역학을 앞으로 발전시킬 것이지만 먼저 이를 계산하는 함수(푸아송 노이즈 샘플링 포함)를 정의하겠습니다.
def sample_state_deltas(
state, population, mobility_matrix, params, seed, is_deterministic=False):
"""Computes one-step change in state, including Poisson sampling.
Note that this is coded to support vectorized evaluation on arbitrary-shape
batches of states. This is useful, for example, for running multiple
independent replicas of this model to compute credible intervals for the
parameters. We refer to the arbitrary batch shape with the conventional
`B` in the parameter documentation below. This function also, of course,
supports broadcasting over the batch shape.
Args:
state: A `SEIRComponents` tuple with fields Tensors of shape
B + [num_locations] giving the current disease state.
population: A Tensor of shape B + [num_locations] giving the current city
populations.
mobility_matrix: A Tensor of shape B + [num_locations, num_locations] giving
the current baseline inter-city mobility.
params: A `ModelParams` tuple with fields Tensors of shape B giving the
global parameters for the current EAKF run.
seed: Initial entropy for pseudo-random number generation. The Poisson
sampling is repeatable by supplying the same seed.
is_deterministic: A `bool` flag to turn off Poisson sampling if desired.
Returns:
delta: A `SEIRComponents` tuple with fields Tensors of shape
B + [num_locations] giving the one-day changes in the state, according
to equations 1-4 above (including Poisson noise per Li et al).
"""
undocumented_infectious_fraction = state.undocumented_infectious / population
documented_infectious_fraction = state.documented_infectious / population
# Anyone not documented as infectious is considered mobile
mobile_population = (population - state.documented_infectious)
def compute_outflow(compartment_population):
raw_mobility = tf.linalg.matvec(
mobility_matrix, compartment_population / mobile_population)
return params.intercity_underreporting_factor * raw_mobility
def compute_inflow(compartment_population):
raw_mobility = tf.linalg.matmul(
mobility_matrix,
(compartment_population / mobile_population)[..., tf.newaxis],
transpose_a=True)
return params.intercity_underreporting_factor * tf.squeeze(
raw_mobility, axis=-1)
# Helper for sampling the Poisson-variate terms.
seeds = samplers.split_seed(seed, n=11)
if is_deterministic:
def sample_poisson(rate):
return rate
else:
def sample_poisson(rate):
return tfd.Poisson(rate=rate).sample(seed=seeds.pop())
# Below are the various terms called U1-U12 in the paper. We combined the
# first two, which should be fine; both are poisson so their sum is too, and
# there's no risk (as there could be in other terms) of going negative.
susceptible_becoming_exposed = sample_poisson(
state.susceptible *
(params.documented_infectious_tx_rate *
documented_infectious_fraction +
(params.undocumented_infectious_tx_relative_rate *
params.documented_infectious_tx_rate) *
undocumented_infectious_fraction)) # U1 + U2
susceptible_population_inflow = sample_poisson(
compute_inflow(state.susceptible)) # U3
susceptible_population_outflow = sample_poisson(
compute_outflow(state.susceptible)) # U4
exposed_becoming_documented_infectious = sample_poisson(
params.fraction_of_documented_infections *
state.exposed / params.average_latency_period) # U5
exposed_becoming_undocumented_infectious = sample_poisson(
(1 - params.fraction_of_documented_infections) *
state.exposed / params.average_latency_period) # U6
exposed_population_inflow = sample_poisson(
compute_inflow(state.exposed)) # U7
exposed_population_outflow = sample_poisson(
compute_outflow(state.exposed)) # U8
documented_infectious_becoming_recovered = sample_poisson(
state.documented_infectious /
params.average_infection_duration) # U9
undocumented_infectious_becoming_recovered = sample_poisson(
state.undocumented_infectious /
params.average_infection_duration) # U10
undocumented_infectious_population_inflow = sample_poisson(
compute_inflow(state.undocumented_infectious)) # U11
undocumented_infectious_population_outflow = sample_poisson(
compute_outflow(state.undocumented_infectious)) # U12
# The final state_deltas
return SEIRComponents(
# Equation [1]
susceptible=(-susceptible_becoming_exposed +
susceptible_population_inflow +
-susceptible_population_outflow),
# Equation [2]
exposed=(susceptible_becoming_exposed +
-exposed_becoming_documented_infectious +
-exposed_becoming_undocumented_infectious +
exposed_population_inflow +
-exposed_population_outflow),
# Equation [3]
documented_infectious=(
exposed_becoming_documented_infectious +
-documented_infectious_becoming_recovered),
# Equation [4]
undocumented_infectious=(
exposed_becoming_undocumented_infectious +
-undocumented_infectious_becoming_recovered +
undocumented_infectious_population_inflow +
-undocumented_infectious_population_outflow),
# New to-be-documented infectious cases, subject to the delayed
# observation model.
daily_new_documented_infectious=exposed_becoming_documented_infectious)
여기 통합자가 있습니다. 이것은에 통해 PRNG 시드 전달을 제외하고 완전히 표준 sample_state_deltas 위한 룽게 쿠타-메소드 호출이 부분의 각 단계에서 독립적 포아송 노이즈를 얻기 위해 기능한다.
@tf.function(autograph=False)
def rk4_one_step(state, population, mobility_matrix, params, seed):
"""Implement one step of RK4, wrapped around a call to sample_state_deltas."""
# One seed for each RK sub-step
seeds = samplers.split_seed(seed, n=4)
deltas = tf.nest.map_structure(tf.zeros_like, state)
combined_deltas = tf.nest.map_structure(tf.zeros_like, state)
for a, b in zip([1., 2, 2, 1.], [6., 3., 3., 6.]):
next_input = tf.nest.map_structure(
lambda x, delta, a=a: x + delta / a, state, deltas)
deltas = sample_state_deltas(
next_input,
population,
mobility_matrix,
params,
seed=seeds.pop(), is_deterministic=False)
combined_deltas = tf.nest.map_structure(
lambda x, delta, b=b: x + delta / b, combined_deltas, deltas)
return tf.nest.map_structure(
lambda s, delta: s + tf.round(delta),
state, combined_deltas)
초기화
여기에서 우리는 논문에서 초기화 체계를 구현합니다.
Li et al에 따르면 우리의 추론 방식은 반복 필터링 외부 루프(IF-EAKF)로 둘러싸인 앙상블 조정 칼만 필터 내부 루프가 될 것입니다. 계산적으로 이것은 세 가지 종류의 초기화가 필요함을 의미합니다.
- 내부 EAKF의 초기 상태
- 첫 번째 EAKF의 초기 매개변수이기도 한 외부 IF의 초기 매개변수
- 첫 번째가 아닌 각 EAKF에 대한 초기 매개변수 역할을 하는 한 IF 반복에서 다음 반복으로 매개변수 업데이트.
def initialize_state(num_particles, num_batches, seed):
"""Initialize the state for a batch of EAKF runs.
Args:
num_particles: `int` giving the number of particles for the EAKF.
num_batches: `int` giving the number of independent EAKF runs to
initialize in a vectorized batch.
seed: PRNG entropy.
Returns:
state: A `SEIRComponents` tuple with Tensors of shape [num_particles,
num_batches, num_cities] giving the initial conditions in each
city, in each filter particle, in each batch member.
"""
num_cities = mobility_matrix_over_time.shape[-2]
state_shape = [num_particles, num_batches, num_cities]
susceptible = initial_population * np.ones(state_shape, dtype=np.float32)
documented_infectious = np.zeros(state_shape, dtype=np.float32)
daily_new_documented_infectious = np.zeros(state_shape, dtype=np.float32)
# Following Li et al, initialize Wuhan with up to 2000 people exposed
# and another up to 2000 undocumented infectious.
rng = np.random.RandomState(seed[0] % (2**31 - 1))
wuhan_exposed = rng.randint(
0, 2001, [num_particles, num_batches]).astype(np.float32)
wuhan_undocumented_infectious = rng.randint(
0, 2001, [num_particles, num_batches]).astype(np.float32)
# Also following Li et al, initialize cities adjacent to Wuhan with three
# days' worth of additional exposed and undocumented-infectious cases,
# as they may have traveled there before the beginning of the modeling
# period.
exposed = 3 * mobility_matrix_over_time[
WUHAN_IDX, :, 0] * wuhan_exposed[
..., np.newaxis] / initial_population[WUHAN_IDX]
undocumented_infectious = 3 * mobility_matrix_over_time[
WUHAN_IDX, :, 0] * wuhan_undocumented_infectious[
..., np.newaxis] / initial_population[WUHAN_IDX]
exposed[..., WUHAN_IDX] = wuhan_exposed
undocumented_infectious[..., WUHAN_IDX] = wuhan_undocumented_infectious
# Following Li et al, we do not remove the inital exposed and infectious
# persons from the susceptible population.
return SEIRComponents(
susceptible=tf.constant(susceptible),
exposed=tf.constant(exposed),
documented_infectious=tf.constant(documented_infectious),
undocumented_infectious=tf.constant(undocumented_infectious),
daily_new_documented_infectious=tf.constant(daily_new_documented_infectious))
def initialize_params(num_particles, num_batches, seed):
"""Initialize the global parameters for the entire inference run.
Args:
num_particles: `int` giving the number of particles for the EAKF.
num_batches: `int` giving the number of independent EAKF runs to
initialize in a vectorized batch.
seed: PRNG entropy.
Returns:
params: A `ModelParams` tuple with fields Tensors of shape
[num_particles, num_batches] giving the global parameters
to use for the first batch of EAKF runs.
"""
# We have 6 parameters. We'll initialize with a Sobol sequence,
# covering the hyper-rectangle defined by our parameter limits.
halton_sequence = tfp.mcmc.sample_halton_sequence(
dim=6, num_results=num_particles * num_batches, seed=seed)
halton_sequence = tf.reshape(
halton_sequence, [num_particles, num_batches, 6])
halton_sequences = tf.nest.pack_sequence_as(
PARAMETER_LOWER_BOUNDS, tf.split(
halton_sequence, num_or_size_splits=6, axis=-1))
def interpolate(minval, maxval, h):
return (maxval - minval) * h + minval
return tf.nest.map_structure(
interpolate,
PARAMETER_LOWER_BOUNDS, PARAMETER_UPPER_BOUNDS, halton_sequences)
def update_params(num_particles, num_batches,
prev_params, parameter_variance, seed):
"""Update the global parameters between EAKF runs.
Args:
num_particles: `int` giving the number of particles for the EAKF.
num_batches: `int` giving the number of independent EAKF runs to
initialize in a vectorized batch.
prev_params: A `ModelParams` tuple of the parameters used for the previous
EAKF run.
parameter_variance: A `ModelParams` tuple specifying how much to drift
each parameter.
seed: PRNG entropy.
Returns:
params: A `ModelParams` tuple with fields Tensors of shape
[num_particles, num_batches] giving the global parameters
to use for the next batch of EAKF runs.
"""
# Initialize near the previous set of parameters. This is the first step
# in Iterated Filtering.
seeds = tf.nest.pack_sequence_as(
prev_params, samplers.split_seed(seed, n=len(prev_params)))
return tf.nest.map_structure(
lambda x, v, seed: x + tf.math.sqrt(v) * tf.random.stateless_normal([
num_particles, num_batches, 1], seed=seed),
prev_params, parameter_variance, seeds)
지연
이 모델의 중요한 특징 중 하나는 감염이 시작보다 늦게 보고된다는 사실을 명시적으로 고려하는 것입니다. 즉 우리가에서 이동하는 사람이 기대된다 \(E\) 받는 구획 \(I^r\) 일에 구획 \(t\) 일부 나중에 날까지 관찰보고 된 경우 카운트에 표시되지 않을 수도 있습니다.
지연이 감마 분포라고 가정합니다. Li et al에 따르면 모양에 1.85를 사용하고 비율을 매개변수화하여 평균 보고 지연 9일을 생성합니다.
def raw_reporting_delay_distribution(gamma_shape=1.85, reporting_delay=9.):
return tfp.distributions.Gamma(
concentration=gamma_shape, rate=gamma_shape / reporting_delay)
우리의 관찰은 불연속적이므로 원시(연속) 지연을 가장 가까운 날까지 반올림합니다. 우리는 또한 유한한 데이터 지평선을 가지고 있으므로 한 사람에 대한 지연 분포는 남은 날 동안 범주형입니다. 따라서 우리는 샘플링보다 더 효율적으로 당 도시 예측 관찰을 계산할 수 \(O(I^r)\) 대신 미리 계산 다항 지연 확률에 의해, 감마을.
def reporting_delay_probs(num_timesteps, gamma_shape=1.85, reporting_delay=9.):
gamma_dist = raw_reporting_delay_distribution(gamma_shape, reporting_delay)
multinomial_probs = [gamma_dist.cdf(1.)]
for k in range(2, num_timesteps + 1):
multinomial_probs.append(gamma_dist.cdf(k) - gamma_dist.cdf(k - 1))
# For samples that are larger than T.
multinomial_probs.append(gamma_dist.survival_function(num_timesteps))
multinomial_probs = tf.stack(multinomial_probs)
return multinomial_probs
다음은 새로운 일일 문서화 감염 수에 이러한 지연을 실제로 적용하는 코드입니다.
def delay_reporting(
daily_new_documented_infectious, num_timesteps, t, multinomial_probs, seed):
# This is the distribution of observed infectious counts from the current
# timestep.
raw_delays = tfd.Multinomial(
total_count=daily_new_documented_infectious,
probs=multinomial_probs).sample(seed=seed)
# The last bucket is used for samples that are out of range of T + 1. Thus
# they are not going to be observable in this model.
clipped_delays = raw_delays[..., :-1]
# We can also remove counts that are such that t + i >= T.
clipped_delays = clipped_delays[..., :num_timesteps - t]
# We finally shift everything by t. That means prepending with zeros.
return tf.concat([
tf.zeros(
tf.concat([
tf.shape(clipped_delays)[:-1], [t]], axis=0),
dtype=clipped_delays.dtype),
clipped_delays], axis=-1)
추론
먼저 추론을 위한 몇 가지 데이터 구조를 정의합니다.
특히, 추론을 수행하는 동안 상태와 매개변수를 함께 패키지하는 반복 필터링을 원할 것입니다. 그래서 우리는 정의 할 것이다 ParameterStatePair 개체를.
우리는 또한 모든 부가 정보를 모델에 패키징하고 싶습니다.
ParameterStatePair = collections.namedtuple(
'ParameterStatePair', ['state', 'params'])
# Info that is tracked and mutated but should not have inference performed over.
SideInfo = collections.namedtuple(
'SideInfo', [
# Observations at every time step.
'observations_over_time',
'initial_population',
'mobility_matrix_over_time',
'population',
# Used for variance of measured observations.
'actual_reported_cases',
# Pre-computed buckets for the multinomial distribution.
'multinomial_probs',
'seed',
])
# Cities can not fall below this fraction of people
MINIMUM_CITY_FRACTION = 0.6
# How much to inflate the covariance by.
INFLATION_FACTOR = 1.1
INFLATE_FN = tfes.inflate_by_scaled_identity_fn(INFLATION_FACTOR)
다음은 Ensemble Kalman Filter용으로 패키징된 완전한 관찰 모델입니다.
흥미로운 기능은 보고 지연(이전과 같이 계산됨)입니다. 상류 모델은 방출 daily_new_documented_infectious 각 시간 단계에서 각 도시에 대한.
# We observe the observed infections.
def observation_fn(t, state_params, extra):
"""Generate reported cases.
Args:
state_params: A `ParameterStatePair` giving the current parameters
and state.
t: Integer giving the current time.
extra: A `SideInfo` carrying auxiliary information.
Returns:
observations: A Tensor of predicted observables, namely new cases
per city at time `t`.
extra: Update `SideInfo`.
"""
# Undo padding introduced in `inference`.
daily_new_documented_infectious = state_params.state.daily_new_documented_infectious[..., 0]
# Number of people that we have already committed to become
# observed infectious over time.
# shape: batch + [num_particles, num_cities, time]
observations_over_time = extra.observations_over_time
num_timesteps = observations_over_time.shape[-1]
seed, new_seed = samplers.split_seed(extra.seed, salt='reporting delay')
daily_delayed_counts = delay_reporting(
daily_new_documented_infectious, num_timesteps, t,
extra.multinomial_probs, seed)
observations_over_time = observations_over_time + daily_delayed_counts
extra = extra._replace(
observations_over_time=observations_over_time,
seed=new_seed)
# Actual predicted new cases, re-padded.
adjusted_observations = observations_over_time[..., t][..., tf.newaxis]
# Finally observations have variance that is a function of the true observations:
return tfd.MultivariateNormalDiag(
loc=adjusted_observations,
scale_diag=tf.math.maximum(
2., extra.actual_reported_cases[..., t][..., tf.newaxis] / 2.)), extra
여기에서 전환 역학을 정의합니다. 우리는 이미 의미론적 작업을 완료했습니다. 여기에서는 EAKF 프레임워크용으로 패키지화하고 Li et al에 따라 도시 인구가 너무 작아지는 것을 방지하기 위해 잘라냅니다.
def transition_fn(t, state_params, extra):
"""SEIR dynamics.
Args:
state_params: A `ParameterStatePair` giving the current parameters
and state.
t: Integer giving the current time.
extra: A `SideInfo` carrying auxiliary information.
Returns:
state_params: A `ParameterStatePair` predicted for the next time step.
extra: Updated `SideInfo`.
"""
mobility_t = extra.mobility_matrix_over_time[..., t]
new_seed, rk4_seed = samplers.split_seed(extra.seed, salt='Transition')
new_state = rk4_one_step(
state_params.state,
extra.population,
mobility_t,
state_params.params,
seed=rk4_seed)
# Make sure population doesn't go below MINIMUM_CITY_FRACTION.
new_population = (
extra.population + state_params.params.intercity_underreporting_factor * (
# Inflow
tf.reduce_sum(mobility_t, axis=-2) -
# Outflow
tf.reduce_sum(mobility_t, axis=-1)))
new_population = tf.where(
new_population < MINIMUM_CITY_FRACTION * extra.initial_population,
extra.initial_population * MINIMUM_CITY_FRACTION,
new_population)
extra = extra._replace(population=new_population, seed=new_seed)
# The Ensemble Kalman Filter code expects the transition function to return a distribution.
# As the dynamics and noise are encapsulated above, we construct a `JointDistribution` that when
# sampled, returns the values above.
new_state = tfd.JointDistributionNamed(
model=tf.nest.map_structure(lambda x: tfd.VectorDeterministic(x), new_state))
params = tfd.JointDistributionNamed(
model=tf.nest.map_structure(lambda x: tfd.VectorDeterministic(x), state_params.params))
state_params = tfd.JointDistributionNamed(
model=ParameterStatePair(state=new_state, params=params))
return state_params, extra
마지막으로 추론 방법을 정의합니다. 이것은 두 개의 루프입니다. 외부 루프는 반복 필터링이고 내부 루프는 앙상블 조정 칼만 필터링입니다.
# Use tf.function to speed up EAKF prediction and updates.
ensemble_kalman_filter_predict = tf.function(
tfes.ensemble_kalman_filter_predict, autograph=False)
ensemble_adjustment_kalman_filter_update = tf.function(
tfes.ensemble_adjustment_kalman_filter_update, autograph=False)
def inference(
num_ensembles,
num_batches,
num_iterations,
actual_reported_cases,
mobility_matrix_over_time,
seed=None,
# This is how much to reduce the variance by in every iterative
# filtering step.
variance_shrinkage_factor=0.9,
# Days before infection is reported.
reporting_delay=9.,
# Shape parameter of Gamma distribution.
gamma_shape_parameter=1.85):
"""Inference for the Shaman, et al. model.
Args:
num_ensembles: Number of particles to use for EAKF.
num_batches: Number of batches of IF-EAKF to run.
num_iterations: Number of iterations to run iterative filtering.
actual_reported_cases: `Tensor` of shape `[L, T]` where `L` is the number
of cities, and `T` is the timesteps.
mobility_matrix_over_time: `Tensor` of shape `[L, L, T]` which specifies the
mobility between locations over time.
variance_shrinkage_factor: Python `float`. How much to reduce the
variance each iteration of iterated filtering.
reporting_delay: Python `float`. How many days before the infection
is reported.
gamma_shape_parameter: Python `float`. Shape parameter of Gamma distribution
of reporting delays.
Returns:
result: A `ModelParams` with fields Tensors of shape [num_batches],
containing the inferred parameters at the final iteration.
"""
print('Starting inference.')
num_timesteps = actual_reported_cases.shape[-1]
params_per_iter = []
multinomial_probs = reporting_delay_probs(
num_timesteps, gamma_shape_parameter, reporting_delay)
seed = samplers.sanitize_seed(seed, salt='Inference')
for i in range(num_iterations):
start_if_time = time.time()
seeds = samplers.split_seed(seed, n=4, salt='Initialize')
if params_per_iter:
parameter_variance = tf.nest.map_structure(
lambda minval, maxval: variance_shrinkage_factor ** (
2 * i) * (maxval - minval) ** 2 / 4.,
PARAMETER_LOWER_BOUNDS, PARAMETER_UPPER_BOUNDS)
params_t = update_params(
num_ensembles,
num_batches,
prev_params=params_per_iter[-1],
parameter_variance=parameter_variance,
seed=seeds.pop())
else:
params_t = initialize_params(num_ensembles, num_batches, seed=seeds.pop())
state_t = initialize_state(num_ensembles, num_batches, seed=seeds.pop())
population_t = sum(x for x in state_t)
observations_over_time = tf.zeros(
[num_ensembles,
num_batches,
actual_reported_cases.shape[0], num_timesteps])
extra = SideInfo(
observations_over_time=observations_over_time,
initial_population=tf.identity(population_t),
mobility_matrix_over_time=mobility_matrix_over_time,
population=population_t,
multinomial_probs=multinomial_probs,
actual_reported_cases=actual_reported_cases,
seed=seeds.pop())
# Clip states
state_t = clip_state(state_t, population_t)
params_t = clip_params(params_t, seed=seeds.pop())
# Accrue the parameter over time. We'll be averaging that
# and using that as our MLE estimate.
params_over_time = tf.nest.map_structure(
lambda x: tf.identity(x), params_t)
state_params = ParameterStatePair(state=state_t, params=params_t)
eakf_state = tfes.EnsembleKalmanFilterState(
step=tf.constant(0), particles=state_params, extra=extra)
for j in range(num_timesteps):
seeds = samplers.split_seed(eakf_state.extra.seed, n=3)
extra = extra._replace(seed=seeds.pop())
# Predict step.
# Inflate and clip.
new_particles = INFLATE_FN(eakf_state.particles)
state_t = clip_state(new_particles.state, eakf_state.extra.population)
params_t = clip_params(new_particles.params, seed=seeds.pop())
eakf_state = eakf_state._replace(
particles=ParameterStatePair(params=params_t, state=state_t))
eakf_predict_state = ensemble_kalman_filter_predict(eakf_state, transition_fn)
# Clip the state and particles.
state_params = eakf_predict_state.particles
state_t = clip_state(
state_params.state, eakf_predict_state.extra.population)
state_params = ParameterStatePair(state=state_t, params=state_params.params)
# We preprocess the state and parameters by affixing a 1 dimension. This is because for
# inference, we treat each city as independent. We could also introduce localization by
# considering cities that are adjacent.
state_params = tf.nest.map_structure(lambda x: x[..., tf.newaxis], state_params)
eakf_predict_state = eakf_predict_state._replace(particles=state_params)
# Update step.
eakf_update_state = ensemble_adjustment_kalman_filter_update(
eakf_predict_state,
actual_reported_cases[..., j][..., tf.newaxis],
observation_fn)
state_params = tf.nest.map_structure(
lambda x: x[..., 0], eakf_update_state.particles)
# Clip to ensure parameters / state are well constrained.
state_t = clip_state(
state_params.state, eakf_update_state.extra.population)
# Finally for the parameters, we should reduce over all updates. We get
# an extra dimension back so let's do that.
params_t = tf.nest.map_structure(
lambda x, y: x + tf.reduce_sum(y[..., tf.newaxis] - x, axis=-2, keepdims=True),
eakf_predict_state.particles.params, state_params.params)
params_t = clip_params(params_t, seed=seeds.pop())
params_t = tf.nest.map_structure(lambda x: x[..., 0], params_t)
state_params = ParameterStatePair(state=state_t, params=params_t)
eakf_state = eakf_update_state
eakf_state = eakf_state._replace(particles=state_params)
# Flatten and collect the inferred parameter at time step t.
params_over_time = tf.nest.map_structure(
lambda s, x: tf.concat([s, x], axis=-1), params_over_time, params_t)
est_params = tf.nest.map_structure(
# Take the average over the Ensemble and over time.
lambda x: tf.math.reduce_mean(x, axis=[0, -1])[..., tf.newaxis],
params_over_time)
params_per_iter.append(est_params)
print('Iterated Filtering {} / {} Ran in: {:.2f} seconds'.format(
i, num_iterations, time.time() - start_if_time))
return tf.nest.map_structure(
lambda x: tf.squeeze(x, axis=-1), params_per_iter[-1])
최종 세부 사항: 매개변수와 상태를 클리핑하는 것은 범위 내에 있고 음수가 아닌지 확인하는 것으로 구성됩니다.
def clip_state(state, population):
"""Clip state to sensible values."""
state = tf.nest.map_structure(
lambda x: tf.where(x < 0, 0., x), state)
# If S > population, then adjust as well.
susceptible = tf.where(state.susceptible > population, population, state.susceptible)
return SEIRComponents(
susceptible=susceptible,
exposed=state.exposed,
documented_infectious=state.documented_infectious,
undocumented_infectious=state.undocumented_infectious,
daily_new_documented_infectious=state.daily_new_documented_infectious)
def clip_params(params, seed):
"""Clip parameters to bounds."""
def _clip(p, minval, maxval):
return tf.where(
p < minval,
minval * (1. + 0.1 * tf.random.stateless_uniform(p.shape, seed=seed)),
tf.where(p > maxval,
maxval * (1. - 0.1 * tf.random.stateless_uniform(
p.shape, seed=seed)), p))
params = tf.nest.map_structure(
_clip, params, PARAMETER_LOWER_BOUNDS, PARAMETER_UPPER_BOUNDS)
return params
모두 함께 실행
# Let's sample the parameters.
#
# NOTE: Li et al. run inference 1000 times, which would take a few hours.
# Here we run inference 30 times (in a single, vectorized batch).
best_parameters = inference(
num_ensembles=300,
num_batches=30,
num_iterations=10,
actual_reported_cases=observed_daily_infectious_count,
mobility_matrix_over_time=mobility_matrix_over_time)
Starting inference. Iterated Filtering 0 / 10 Ran in: 26.65 seconds Iterated Filtering 1 / 10 Ran in: 28.69 seconds Iterated Filtering 2 / 10 Ran in: 28.06 seconds Iterated Filtering 3 / 10 Ran in: 28.48 seconds Iterated Filtering 4 / 10 Ran in: 28.57 seconds Iterated Filtering 5 / 10 Ran in: 28.35 seconds Iterated Filtering 6 / 10 Ran in: 28.35 seconds Iterated Filtering 7 / 10 Ran in: 28.19 seconds Iterated Filtering 8 / 10 Ran in: 28.58 seconds Iterated Filtering 9 / 10 Ran in: 28.23 seconds
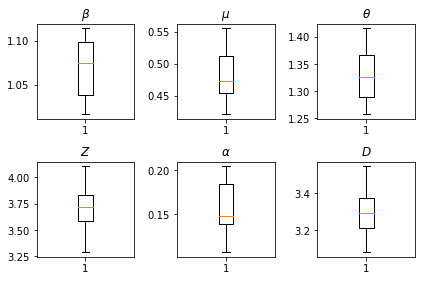
우리의 추론 결과. 모든 글로벌 paramters이 우리를 통해 자신의 변화를 보여주기 위해 우리는 최대 우도 값을 플롯 num_batches 추론 독립적으로 실행됩니다. 이는 보충 자료의 표 S1에 해당합니다.
fig, axs = plt.subplots(2, 3)
axs[0, 0].boxplot(best_parameters.documented_infectious_tx_rate,
whis=(2.5,97.5), sym='')
axs[0, 0].set_title(r'$\beta$')
axs[0, 1].boxplot(best_parameters.undocumented_infectious_tx_relative_rate,
whis=(2.5,97.5), sym='')
axs[0, 1].set_title(r'$\mu$')
axs[0, 2].boxplot(best_parameters.intercity_underreporting_factor,
whis=(2.5,97.5), sym='')
axs[0, 2].set_title(r'$\theta$')
axs[1, 0].boxplot(best_parameters.average_latency_period,
whis=(2.5,97.5), sym='')
axs[1, 0].set_title(r'$Z$')
axs[1, 1].boxplot(best_parameters.fraction_of_documented_infections,
whis=(2.5,97.5), sym='')
axs[1, 1].set_title(r'$\alpha$')
axs[1, 2].boxplot(best_parameters.average_infection_duration,
whis=(2.5,97.5), sym='')
axs[1, 2].set_title(r'$D$')
plt.tight_layout()