 TensorFlow.org で表示 TensorFlow.org で表示
|
 Google Colabで実行 Google Colabで実行
|
 GitHubでソースを表示 GitHubでソースを表示 |
 ノートブックをダウンロード ノートブックをダウンロード |
このチュートリアルでは、基本、画像のノイズ除去、異常検出の3つの例を使用してオートエンコーダを紹介します。
オートエンコーダは、入力を出力にコピーするようにトレーニングされた特殊なタイプのニューラルネットワークです。たとえば、手書きの数字の画像が与えられた場合、オートエンコーダは最初に画像を低次元の潜在表現にエンコードし、次に潜在表現をデコードして画像に戻します。オートエンコーダは、再構成エラーを最小限に抑えながらデータを圧縮することを学習します。
オートエンコーダの詳細については、Ian Goodfellow、Yoshua Bengio、AaronCourville によるディープラーニングの第 14 章を参照してください。
TensorFlow とその他のライブラリをインポートする
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers, losses
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Model
2024-01-11 23:00:50.693016: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:9261] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2024-01-11 23:00:50.693063: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:607] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2024-01-11 23:00:50.694811: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1515] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
データセットを読み込む
まず、Fashion MNIST データセットを使用して基本的なオートエンコーダーをトレーニングします。このデータセットの各画像は 28x28 ピクセルです。
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
print (x_train.shape)
print (x_test.shape)
(60000, 28, 28) (10000, 28, 28)
最初の例:オートエンコーダの基本

次の2つの高密度レイヤーでオートエンコーダーを定義します。encoder は、画像を 64 次元の潜在ベクトルに圧縮します。decoder は、潜在空間から元の画像を再構築します。
モデルを定義するには、Keras Model Subclassing API を使用します。
class Autoencoder(Model):
def __init__(self, latent_dim, shape):
super(Autoencoder, self).__init__()
self.latent_dim = latent_dim
self.shape = shape
self.encoder = tf.keras.Sequential([
layers.Flatten(),
layers.Dense(latent_dim, activation='relu'),
])
self.decoder = tf.keras.Sequential([
layers.Dense(tf.math.reduce_prod(shape), activation='sigmoid'),
layers.Reshape(shape)
])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
shape = x_test.shape[1:]
latent_dim = 64
autoencoder = Autoencoder(latent_dim, shape)
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
入力とターゲットの両方として x_train を使用してモデルをトレーニングします。encoder は、データセットを 784 次元から潜在空間に圧縮することを学習し、decoder は元の画像を再構築することを学習します。
autoencoder.fit(x_train, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test, x_test))
Epoch 1/10 WARNING: All log messages before absl::InitializeLog() is called are written to STDERR I0000 00:00:1705014057.892644 1057381 device_compiler.h:186] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process. 1875/1875 [==============================] - 6s 2ms/step - loss: 0.0237 - val_loss: 0.0136 Epoch 2/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0117 - val_loss: 0.0106 Epoch 3/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0100 - val_loss: 0.0098 Epoch 4/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0094 - val_loss: 0.0093 Epoch 5/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0092 - val_loss: 0.0092 Epoch 6/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0090 - val_loss: 0.0090 Epoch 7/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0089 - val_loss: 0.0090 Epoch 8/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0088 - val_loss: 0.0089 Epoch 9/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0088 - val_loss: 0.0090 Epoch 10/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0087 - val_loss: 0.0089 <keras.src.callbacks.History at 0x7f80d8850eb0>
モデルがトレーニングされたので、テストセットから画像をエンコードおよびデコードしてモデルをテストします。
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test[i])
plt.title("original")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i])
plt.title("reconstructed")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

2番目の例:画像のノイズ除去

オートエンコーダは、画像からノイズを除去するようにトレーニングすることもできます。 次のセクションでは、各画像にランダムノイズを適用して、ノイズの多いバージョンの FashionMNIST データセットを作成します。次に、ノイズの多い画像を入力として使用し、元の画像をターゲットとして使用して、オートエンコーダーをトレーニングします。
データセットを再インポートして、以前に行った変更を省略しましょう。
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train[..., tf.newaxis]
x_test = x_test[..., tf.newaxis]
print(x_train.shape)
(60000, 28, 28, 1)
画像にランダムノイズを追加します
noise_factor = 0.2
x_train_noisy = x_train + noise_factor * tf.random.normal(shape=x_train.shape)
x_test_noisy = x_test + noise_factor * tf.random.normal(shape=x_test.shape)
x_train_noisy = tf.clip_by_value(x_train_noisy, clip_value_min=0., clip_value_max=1.)
x_test_noisy = tf.clip_by_value(x_test_noisy, clip_value_min=0., clip_value_max=1.)
ノイズの多い画像をプロットします。
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
plt.show()

畳み込みオートエンコーダーを定義します。
この例では、encoder の Conv2D レイヤーと、decoder の Conv2DTranspose レイヤーを使用して畳み込みオートエンコーダーをトレーニングします。
class Denoise(Model):
def __init__(self):
super(Denoise, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Input(shape=(28, 28, 1)),
layers.Conv2D(16, (3, 3), activation='relu', padding='same', strides=2),
layers.Conv2D(8, (3, 3), activation='relu', padding='same', strides=2)])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2D(1, kernel_size=(3, 3), activation='sigmoid', padding='same')])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Denoise()
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
autoencoder.fit(x_train_noisy, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test_noisy, x_test))
Epoch 1/10 1875/1875 [==============================] - 10s 4ms/step - loss: 0.0181 - val_loss: 0.0105 Epoch 2/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0094 - val_loss: 0.0088 Epoch 3/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0084 - val_loss: 0.0082 Epoch 4/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0079 - val_loss: 0.0077 Epoch 5/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0075 - val_loss: 0.0074 Epoch 6/10 1875/1875 [==============================] - 6s 3ms/step - loss: 0.0073 - val_loss: 0.0074 Epoch 7/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0071 - val_loss: 0.0071 Epoch 8/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0070 - val_loss: 0.0070 Epoch 9/10 1875/1875 [==============================] - 7s 3ms/step - loss: 0.0070 - val_loss: 0.0070 Epoch 10/10 1875/1875 [==============================] - 7s 4ms/step - loss: 0.0069 - val_loss: 0.0069 <keras.src.callbacks.History at 0x7f800c75a490>
エンコーダーの概要を見てみましょう。画像が 28x28 から 7x7 にダウンサンプリングされていることに注目してください。
autoencoder.encoder.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 14, 14, 16) 160
conv2d_1 (Conv2D) (None, 7, 7, 8) 1160
=================================================================
Total params: 1320 (5.16 KB)
Trainable params: 1320 (5.16 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________
デコーダーは画像を 7x7 から 28x28 にアップサンプリングします。
autoencoder.decoder.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_transpose (Conv2DTr (None, 14, 14, 8) 584
anspose)
conv2d_transpose_1 (Conv2D (None, 28, 28, 16) 1168
Transpose)
conv2d_2 (Conv2D) (None, 28, 28, 1) 145
=================================================================
Total params: 1897 (7.41 KB)
Trainable params: 1897 (7.41 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________
オートエンコーダにより生成されたノイズの多い画像とノイズ除去された画像の両方をプロットします。
encoded_imgs = autoencoder.encoder(x_test_noisy).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original + noise
ax = plt.subplot(2, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
bx = plt.subplot(2, n, i + n + 1)
plt.title("reconstructed")
plt.imshow(tf.squeeze(decoded_imgs[i]))
plt.gray()
bx.get_xaxis().set_visible(False)
bx.get_yaxis().set_visible(False)
plt.show()

3番目の例:異常検出
概要
この例では、オートエンコーダーをトレーニングして、ECG5000 データセットの異常を検出します。このデータセットには、5,000 の心電図が含まれ、それぞれに 140 のデータポイントがあります。データセットの簡略化されたバージョンを使用します。各例には、0(異常なリズムに対応)または1(正常なリズムに対応)のいずれかのラベルが付けられています。ここでは異常なリズムを特定することに興味があります。
注意:これはラベル付きのデータセットであるため、教師あり学習の問題と見なせます。この例の目的は、ラベルが使用できない、より大きなデータセットに適用できる異常検出の概念を説明することです(たとえば、数千の正常なリズムがあり、異常なリズムが少数しかない場合)。
オートエンコーダーを使用すると、どのようにして異常を検出できるのでしょうか?オートエンコーダは、再構築エラーを最小限に抑えるようにトレーニングされていることを思い出してください。オートエンコーダーは通常のリズムでのみトレーニングし、それを使用してすべてのデータを再構築します。私たちの仮説は、異常なリズムはより高い再構成エラーを持つだろうということです。次に、再構成エラーが固定しきい値を超えた場合、リズムを異常として分類します。
ECG データを読み込む
使用するデータセットは、timeseriesclassification.com のデータセットに基づいています。
# Download the dataset
dataframe = pd.read_csv('http://storage.googleapis.com/download.tensorflow.org/data/ecg.csv', header=None)
raw_data = dataframe.values
dataframe.head()
# The last element contains the labels
labels = raw_data[:, -1]
# The other data points are the electrocadriogram data
data = raw_data[:, 0:-1]
train_data, test_data, train_labels, test_labels = train_test_split(
data, labels, test_size=0.2, random_state=21
)
データを [0,1] に正規化します。
min_val = tf.reduce_min(train_data)
max_val = tf.reduce_max(train_data)
train_data = (train_data - min_val) / (max_val - min_val)
test_data = (test_data - min_val) / (max_val - min_val)
train_data = tf.cast(train_data, tf.float32)
test_data = tf.cast(test_data, tf.float32)
このデータセットで 1 としてラベル付けされている通常のリズムのみを使用して、オートエンコーダーをトレーニングします。正常なリズムを異常なリズムから分離します。
train_labels = train_labels.astype(bool)
test_labels = test_labels.astype(bool)
normal_train_data = train_data[train_labels]
normal_test_data = test_data[test_labels]
anomalous_train_data = train_data[~train_labels]
anomalous_test_data = test_data[~test_labels]
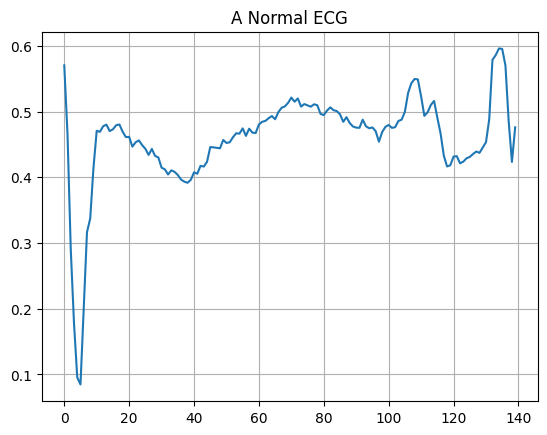
正常な ECG をプロットします。
plt.grid()
plt.plot(np.arange(140), normal_train_data[0])
plt.title("A Normal ECG")
plt.show()
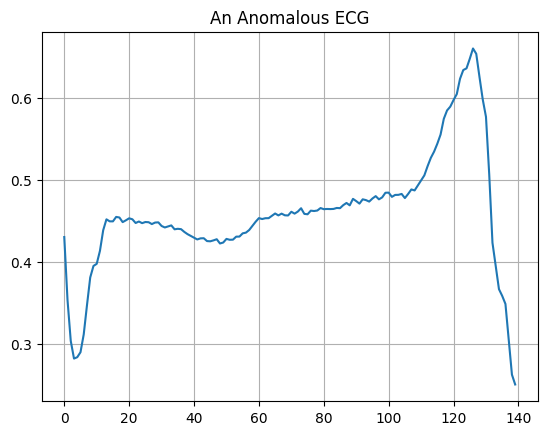
異常な ECG をプロットします。
plt.grid()
plt.plot(np.arange(140), anomalous_train_data[0])
plt.title("An Anomalous ECG")
plt.show()
モデルを構築する
class AnomalyDetector(Model):
def __init__(self):
super(AnomalyDetector, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Dense(32, activation="relu"),
layers.Dense(16, activation="relu"),
layers.Dense(8, activation="relu")])
self.decoder = tf.keras.Sequential([
layers.Dense(16, activation="relu"),
layers.Dense(32, activation="relu"),
layers.Dense(140, activation="sigmoid")])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = AnomalyDetector()
autoencoder.compile(optimizer='adam', loss='mae')
オートエンコーダは通常の ECG のみを使用してトレーニングされますが、完全なテストセットを使用して評価されることに注意してください。
history = autoencoder.fit(normal_train_data, normal_train_data,
epochs=20,
batch_size=512,
validation_data=(test_data, test_data),
shuffle=True)
Epoch 1/20 5/5 [==============================] - 2s 48ms/step - loss: 0.0619 - val_loss: 0.0539 Epoch 2/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0559 - val_loss: 0.0519 Epoch 3/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0539 - val_loss: 0.0501 Epoch 4/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0503 - val_loss: 0.0484 Epoch 5/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0458 - val_loss: 0.0480 Epoch 6/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0421 - val_loss: 0.0453 Epoch 7/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0380 - val_loss: 0.0425 Epoch 8/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0348 - val_loss: 0.0413 Epoch 9/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0322 - val_loss: 0.0404 Epoch 10/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0301 - val_loss: 0.0392 Epoch 11/20 5/5 [==============================] - 0s 17ms/step - loss: 0.0283 - val_loss: 0.0384 Epoch 12/20 5/5 [==============================] - 0s 17ms/step - loss: 0.0269 - val_loss: 0.0376 Epoch 13/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0257 - val_loss: 0.0368 Epoch 14/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0248 - val_loss: 0.0362 Epoch 15/20 5/5 [==============================] - 0s 17ms/step - loss: 0.0240 - val_loss: 0.0355 Epoch 16/20 5/5 [==============================] - 0s 17ms/step - loss: 0.0233 - val_loss: 0.0351 Epoch 17/20 5/5 [==============================] - 0s 17ms/step - loss: 0.0226 - val_loss: 0.0347 Epoch 18/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0221 - val_loss: 0.0344 Epoch 19/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0217 - val_loss: 0.0342 Epoch 20/20 5/5 [==============================] - 0s 16ms/step - loss: 0.0213 - val_loss: 0.0340
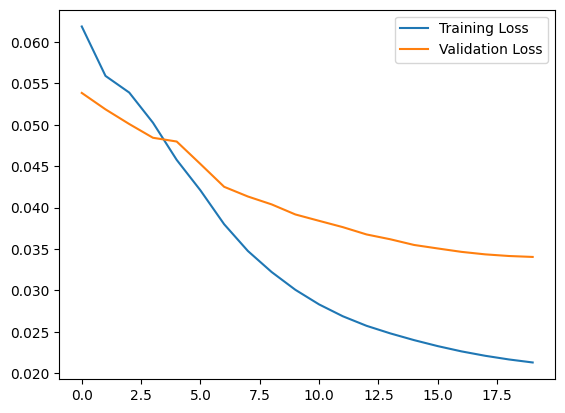
plt.plot(history.history["loss"], label="Training Loss")
plt.plot(history.history["val_loss"], label="Validation Loss")
plt.legend()
<matplotlib.legend.Legend at 0x7f809c6ece50>
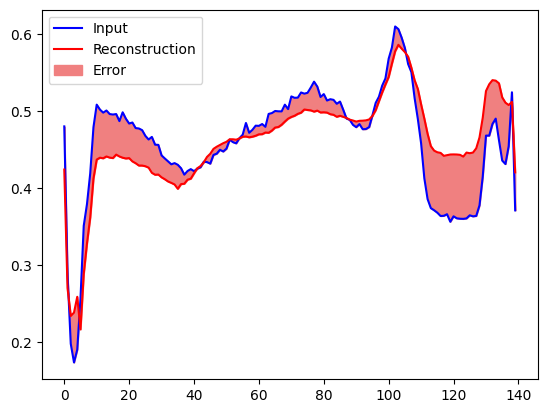
再構成エラーが正常なトレーニング例からの1標準偏差より大きい場合、ECG を異常として分類します。まず、トレーニングセットからの正常な ECG、オートエンコーダーによりエンコードおよびデコードされた後の再構成、および再構成エラーをプロットします。
encoded_data = autoencoder.encoder(normal_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(normal_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], normal_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
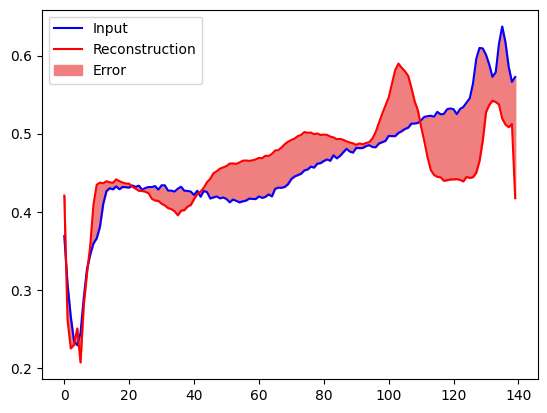
異常なテストサンプルで同様にプロットを作成します。
encoded_data = autoencoder.encoder(anomalous_test_data).numpy()
decoded_data = autoencoder.decoder(encoded_data).numpy()
plt.plot(anomalous_test_data[0], 'b')
plt.plot(decoded_data[0], 'r')
plt.fill_between(np.arange(140), decoded_data[0], anomalous_test_data[0], color='lightcoral')
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
異常を検出します
再構成損失が指定してしきい値より大きいかどうかを計算することにより、異常を検出します。このチュートリアルでは、トレーニングセットから正常なサンプルの平均平均誤差を計算し、再構成誤差がトレーニングセットからの1標準偏差よりも大きい場合、以降のサンプルを異常として分類します。
トレーニングセットからの通常の ECG に再構成エラーをプロットします
reconstructions = autoencoder.predict(normal_train_data)
train_loss = tf.keras.losses.mae(reconstructions, normal_train_data)
plt.hist(train_loss[None,:], bins=50)
plt.xlabel("Train loss")
plt.ylabel("No of examples")
plt.show()
74/74 [==============================] - 0s 1ms/step
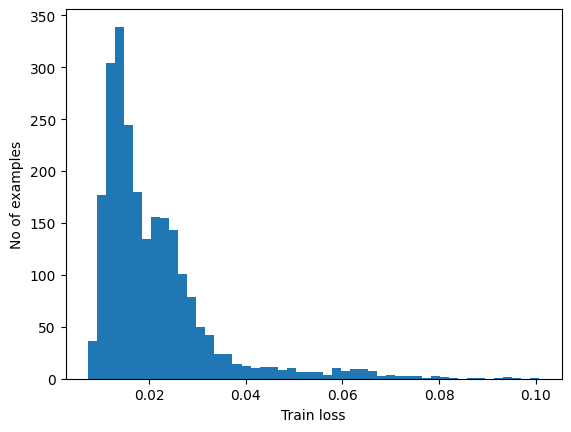
平均より1標準偏差上のしきい値を選択します。
threshold = np.mean(train_loss) + np.std(train_loss)
print("Threshold: ", threshold)
Threshold: 0.0331916
注意: テストサンプルを異常として分類するしきい値を選択するために使用できるアプローチは他にもあります。適切なアプローチはデータセットによって異なります。詳細については、このチュートリアルの最後にあるリンクを参照してください。
テストセットの異常なサンプルの再構成エラーを調べると、ほとんどの場合、再構成エラーはしきい値よりも大きいことがわかります。しきい値を変更することで、分類器の精度とリコールを調整できます。
reconstructions = autoencoder.predict(anomalous_test_data)
test_loss = tf.keras.losses.mae(reconstructions, anomalous_test_data)
plt.hist(test_loss[None, :], bins=50)
plt.xlabel("Test loss")
plt.ylabel("No of examples")
plt.show()
14/14 [==============================] - 0s 2ms/step
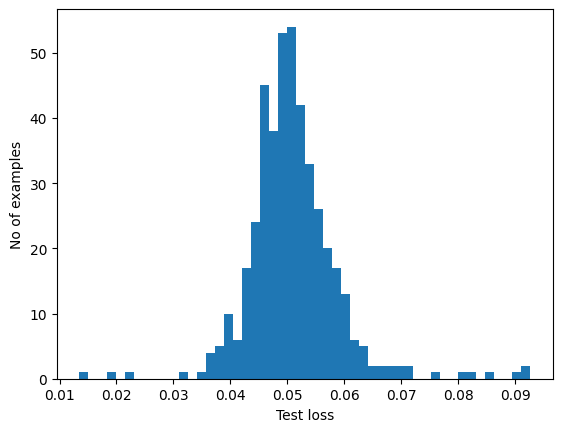
再構成エラーがしきい値よりも大きい場合は、ECG を異常として分類します。
def predict(model, data, threshold):
reconstructions = model(data)
loss = tf.keras.losses.mae(reconstructions, data)
return tf.math.less(loss, threshold)
def print_stats(predictions, labels):
print("Accuracy = {}".format(accuracy_score(labels, predictions)))
print("Precision = {}".format(precision_score(labels, predictions)))
print("Recall = {}".format(recall_score(labels, predictions)))
preds = predict(autoencoder, test_data, threshold)
print_stats(preds, test_labels)
Accuracy = 0.945 Precision = 0.9922027290448343 Recall = 0.9089285714285714
次のステップ
オートエンコーダによる異常検出の詳細については、Victor Dibia が TensorFlow.js で構築したこの優れたインタラクティブな例をご覧ください。実際の使用例については、TensorFlow を使用してAirbus が ISS テレメトリデータの異常を検出する方法を参照してください。基本の詳細については、François Chollet によるこのブログ投稿をご一読ください。詳細については、Ian Goodfellow、Yoshua Bengio、Aaron Courville によるディープラーニングの第 14 章をご覧ください。
