 View on TensorFlow.org View on TensorFlow.org
|
 Run in Google Colab Run in Google Colab
|
 View source on GitHub View source on GitHub
|
 Download notebook Download notebook
|
This tutorial is an introduction to time series forecasting using TensorFlow. It builds a few different styles of models including Convolutional and Recurrent Neural Networks (CNNs and RNNs).
This is covered in two main parts, with subsections:
- Forecast for a single time step:
- A single feature.
- All features.
- Forecast multiple steps:
- Single-shot: Make the predictions all at once.
- Autoregressive: Make one prediction at a time and feed the output back to the model.
Setup
import os
import datetime
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
2024-08-16 02:37:06.588180: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:485] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2024-08-16 02:37:06.609911: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:8454] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2024-08-16 02:37:06.616329: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1452] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
The weather dataset
This tutorial uses a weather time series dataset recorded by the Max Planck Institute for Biogeochemistry.
This dataset contains 14 different features such as air temperature, atmospheric pressure, and humidity. These were collected every 10 minutes, beginning in 2003. For efficiency, you will use only the data collected between 2009 and 2016. This section of the dataset was prepared by François Chollet for his book Deep Learning with Python.
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip 13568290/13568290 ━━━━━━━━━━━━━━━━━━━━ 0s 0us/step
This tutorial will just deal with hourly predictions, so start by sub-sampling the data from 10-minute intervals to one-hour intervals:
df = pd.read_csv(csv_path)
# Slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
Let's take a glance at the data. Here are the first few rows:
df.head()
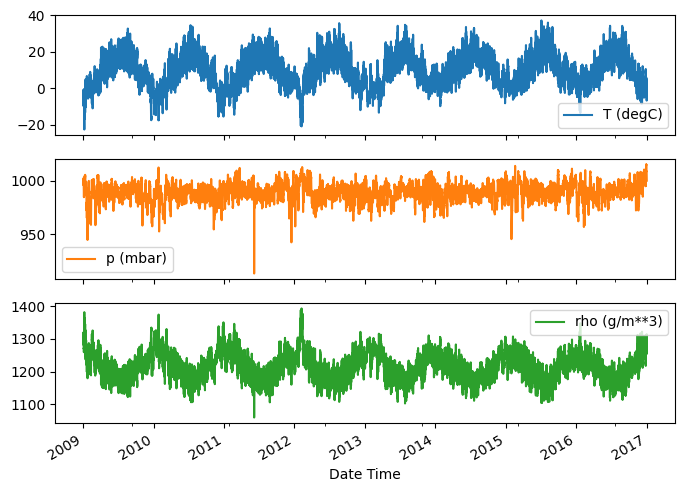
Here is the evolution of a few features over time:
plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)
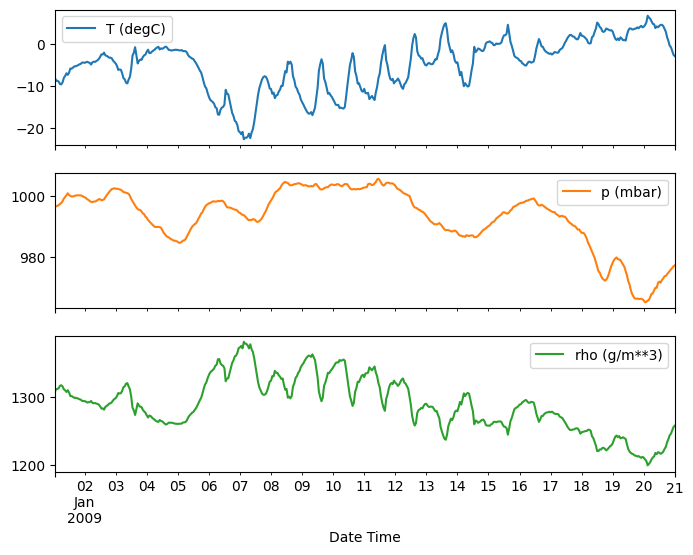
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)
Inspect and cleanup
Next, look at the statistics of the dataset:
df.describe().transpose()
Wind velocity
One thing that should stand out is the min value of the wind velocity (wv (m/s)) and the maximum value (max. wv (m/s)) columns. This -9999 is likely erroneous.
There's a separate wind direction column, so the velocity should be greater than zero (>=0). Replace it with zeros:
wv = df['wv (m/s)']
bad_wv = wv == -9999.0
wv[bad_wv] = 0.0
max_wv = df['max. wv (m/s)']
bad_max_wv = max_wv == -9999.0
max_wv[bad_max_wv] = 0.0
# The above inplace edits are reflected in the DataFrame.
df['wv (m/s)'].min()
0.0
Feature engineering
Before diving in to build a model, it's important to understand your data and be sure that you're passing the model appropriately formatted data.
Wind
The last column of the data, wd (deg)—gives the wind direction in units of degrees. Angles do not make good model inputs: 360° and 0° should be close to each other and wrap around smoothly. Direction shouldn't matter if the wind is not blowing.
Right now the distribution of wind data looks like this:
plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')
Text(0, 0.5, 'Wind Velocity [m/s]')
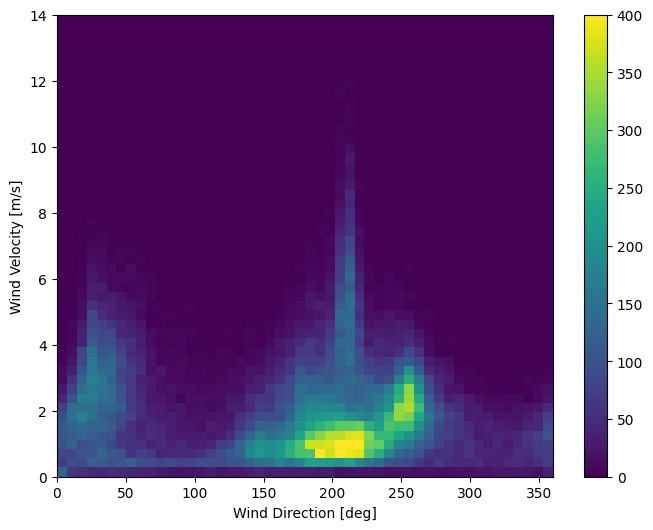
But this will be easier for the model to interpret if you convert the wind direction and velocity columns to a wind vector:
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')
# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180
# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)
# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)
The distribution of wind vectors is much simpler for the model to correctly interpret:
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')
(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)
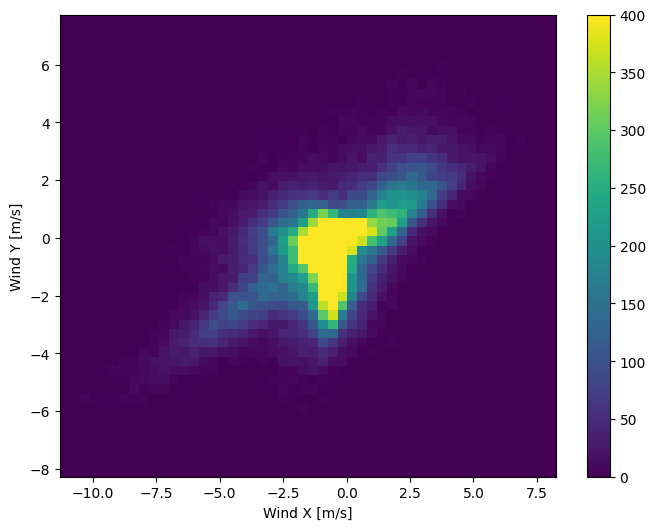
Time
Similarly, the Date Time column is very useful, but not in this string form. Start by converting it to seconds:
timestamp_s = date_time.map(pd.Timestamp.timestamp)
Similar to the wind direction, the time in seconds is not a useful model input. Being weather data, it has clear daily and yearly periodicity. There are many ways you could deal with periodicity.
You can get usable signals by using sine and cosine transforms to clear "Time of day" and "Time of year" signals:
day = 24*60*60
year = (365.2425)*day
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))
plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')
Text(0.5, 1.0, 'Time of day signal')
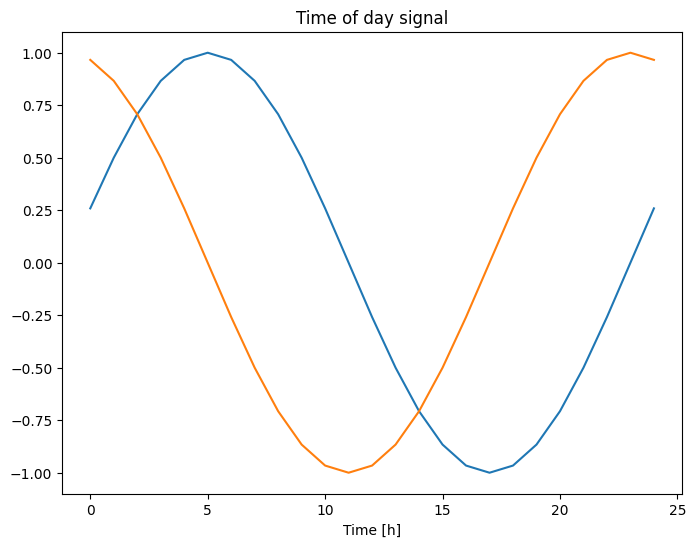
This gives the model access to the most important frequency features. In this case you knew ahead of time which frequencies were important.
If you don't have that information, you can determine which frequencies are important by extracting features with Fast Fourier Transform. To check the assumptions, here is the tf.signal.rfft of the temperature over time. Note the obvious peaks at frequencies near 1/year and 1/day:
fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))
n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)
f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR I0000 00:00:1723775833.614540 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.618414 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.622101 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.625816 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.638786 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.642295 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.645790 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.649212 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.652657 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.656173 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.659653 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775833.663146 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.884491 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.886647 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.888756 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.890846 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.892883 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.894854 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.896838 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.898826 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.900762 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.902728 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.904708 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.906685 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.945076 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.947150 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.949185 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.951205 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.953161 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.955132 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.957121 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.959115 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.961075 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.963543 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.965909 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1723775834.968304 80658 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355

Split the data
You'll use a (70%, 20%, 10%) split for the training, validation, and test sets. Note the data is not being randomly shuffled before splitting. This is for two reasons:
- It ensures that chopping the data into windows of consecutive samples is still possible.
- It ensures that the validation/test results are more realistic, being evaluated on the data collected after the model was trained.
column_indices = {name: i for i, name in enumerate(df.columns)}
n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]
num_features = df.shape[1]
Normalize the data
It is important to scale features before training a neural network. Normalization is a common way of doing this scaling: subtract the mean and divide by the standard deviation of each feature.
The mean and standard deviation should only be computed using the training data so that the models have no access to the values in the validation and test sets.
It's also arguable that the model shouldn't have access to future values in the training set when training, and that this normalization should be done using moving averages. That's not the focus of this tutorial, and the validation and test sets ensure that you get (somewhat) honest metrics. So, in the interest of simplicity this tutorial uses a simple average.
train_mean = train_df.mean()
train_std = train_df.std()
train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std
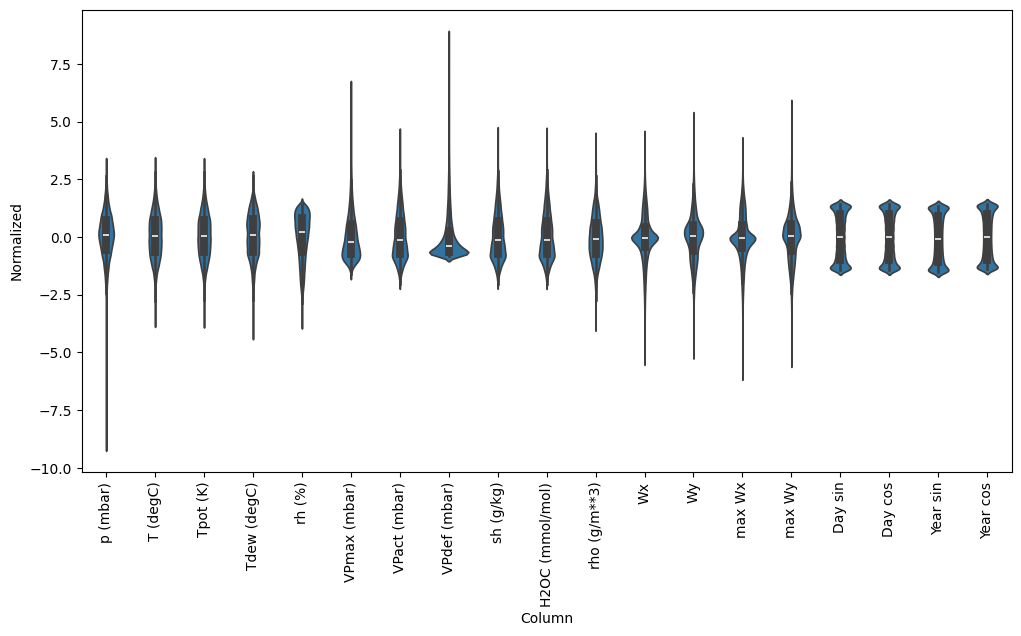
Now, peek at the distribution of the features. Some features do have long tails, but there are no obvious errors like the -9999 wind velocity value.
df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)
/tmpfs/tmp/ipykernel_80658/3214313372.py:5: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator. _ = ax.set_xticklabels(df.keys(), rotation=90)
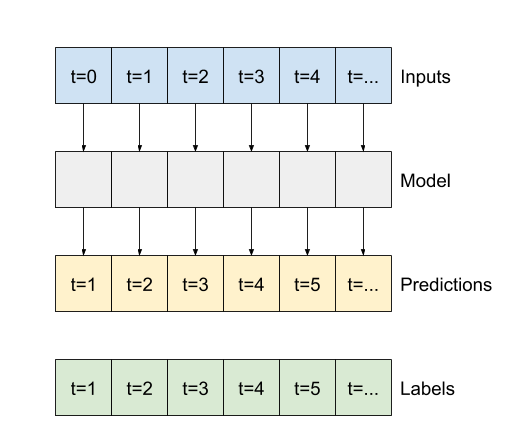
Data windowing
The models in this tutorial will make a set of predictions based on a window of consecutive samples from the data.
The main features of the input windows are:
- The width (number of time steps) of the input and label windows.
- The time offset between them.
- Which features are used as inputs, labels, or both.
This tutorial builds a variety of models (including Linear, DNN, CNN and RNN models), and uses them for both:
- Single-output, and multi-output predictions.
- Single-time-step and multi-time-step predictions.
This section focuses on implementing the data windowing so that it can be reused for all of those models.
Depending on the task and type of model you may want to generate a variety of data windows. Here are some examples:
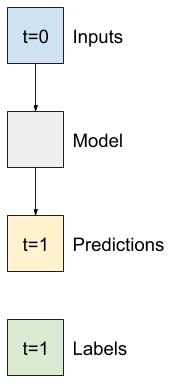
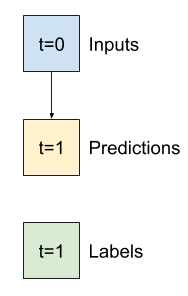
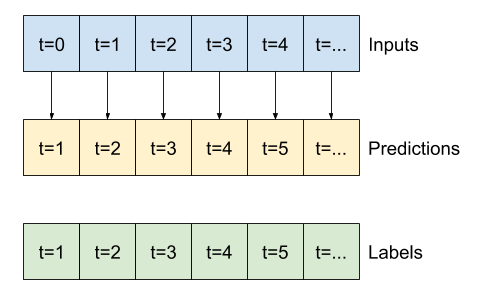
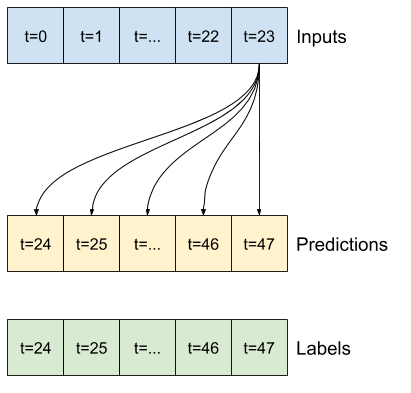
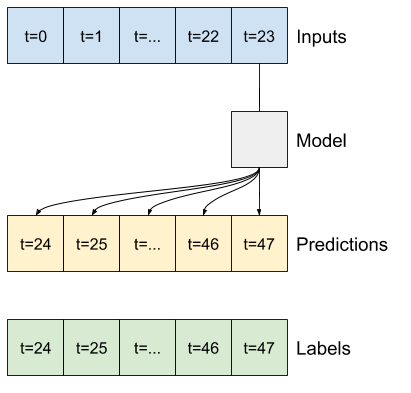
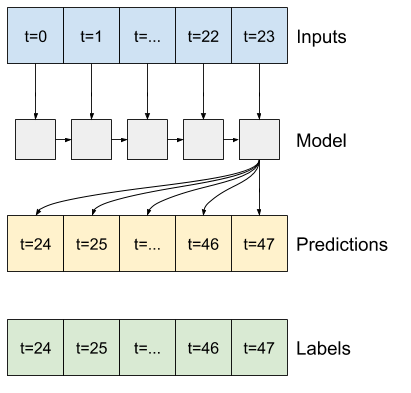
For example, to make a single prediction 24 hours into the future, given 24 hours of history, you might define a window like this:
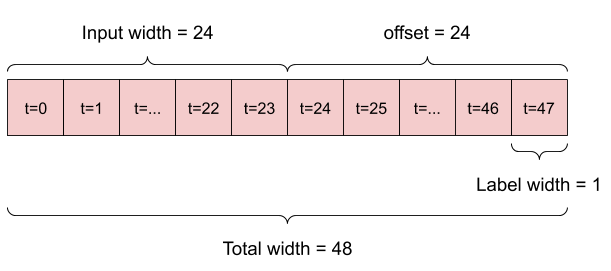
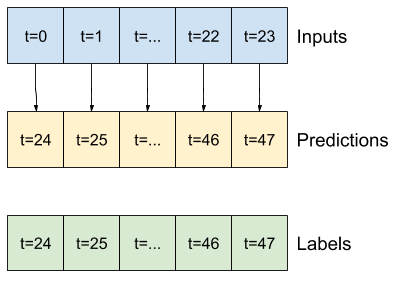
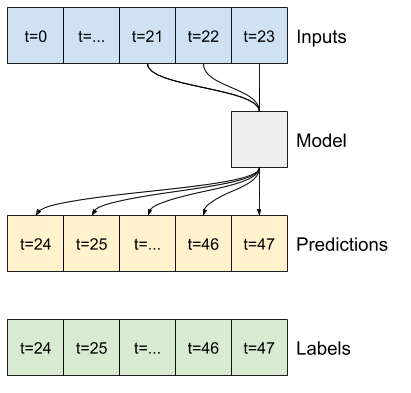
A model that makes a prediction one hour into the future, given six hours of history, would need a window like this:

The rest of this section defines a WindowGenerator class. This class can:
- Handle the indexes and offsets as shown in the diagrams above.
- Split windows of features into
(features, labels)pairs. - Plot the content of the resulting windows.
- Efficiently generate batches of these windows from the training, evaluation, and test data, using
tf.data.Datasets.
1. Indexes and offsets
Start by creating the WindowGenerator class. The __init__ method includes all the necessary logic for the input and label indices.
It also takes the training, evaluation, and test DataFrames as input. These will be converted to tf.data.Datasets of windows later.
class WindowGenerator():
def __init__(self, input_width, label_width, shift,
train_df=train_df, val_df=val_df, test_df=test_df,
label_columns=None):
# Store the raw data.
self.train_df = train_df
self.val_df = val_df
self.test_df = test_df
# Work out the label column indices.
self.label_columns = label_columns
if label_columns is not None:
self.label_columns_indices = {name: i for i, name in
enumerate(label_columns)}
self.column_indices = {name: i for i, name in
enumerate(train_df.columns)}
# Work out the window parameters.
self.input_width = input_width
self.label_width = label_width
self.shift = shift
self.total_window_size = input_width + shift
self.input_slice = slice(0, input_width)
self.input_indices = np.arange(self.total_window_size)[self.input_slice]
self.label_start = self.total_window_size - self.label_width
self.labels_slice = slice(self.label_start, None)
self.label_indices = np.arange(self.total_window_size)[self.labels_slice]
def __repr__(self):
return '\n'.join([
f'Total window size: {self.total_window_size}',
f'Input indices: {self.input_indices}',
f'Label indices: {self.label_indices}',
f'Label column name(s): {self.label_columns}'])
Here is code to create the 2 windows shown in the diagrams at the start of this section:
w1 = WindowGenerator(input_width=24, label_width=1, shift=24,
label_columns=['T (degC)'])
w1
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [47] Label column name(s): ['T (degC)']
w2 = WindowGenerator(input_width=6, label_width=1, shift=1,
label_columns=['T (degC)'])
w2
Total window size: 7 Input indices: [0 1 2 3 4 5] Label indices: [6] Label column name(s): ['T (degC)']
2. Split
Given a list of consecutive inputs, the split_window method will convert them to a window of inputs and a window of labels.
The example w2 you define earlier will be split like this:
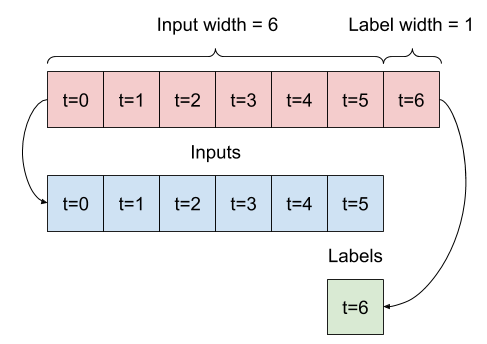
This diagram doesn't show the features axis of the data, but this split_window function also handles the label_columns so it can be used for both the single output and multi-output examples.
def split_window(self, features):
inputs = features[:, self.input_slice, :]
labels = features[:, self.labels_slice, :]
if self.label_columns is not None:
labels = tf.stack(
[labels[:, :, self.column_indices[name]] for name in self.label_columns],
axis=-1)
# Slicing doesn't preserve static shape information, so set the shapes
# manually. This way the `tf.data.Datasets` are easier to inspect.
inputs.set_shape([None, self.input_width, None])
labels.set_shape([None, self.label_width, None])
return inputs, labels
WindowGenerator.split_window = split_window
Try it out:
# Stack three slices, the length of the total window.
example_window = tf.stack([np.array(train_df[:w2.total_window_size]),
np.array(train_df[100:100+w2.total_window_size]),
np.array(train_df[200:200+w2.total_window_size])])
example_inputs, example_labels = w2.split_window(example_window)
print('All shapes are: (batch, time, features)')
print(f'Window shape: {example_window.shape}')
print(f'Inputs shape: {example_inputs.shape}')
print(f'Labels shape: {example_labels.shape}')
All shapes are: (batch, time, features) Window shape: (3, 7, 19) Inputs shape: (3, 6, 19) Labels shape: (3, 1, 1)
Typically, data in TensorFlow is packed into arrays where the outermost index is across examples (the "batch" dimension). The middle indices are the "time" or "space" (width, height) dimension(s). The innermost indices are the features.
The code above took a batch of three 7-time step windows with 19 features at each time step. It splits them into a batch of 6-time step 19-feature inputs, and a 1-time step 1-feature label. The label only has one feature because the WindowGenerator was initialized with label_columns=['T (degC)']. Initially, this tutorial will build models that predict single output labels.
3. Plot
Here is a plot method that allows a simple visualization of the split window:
w2.example = example_inputs, example_labels
def plot(self, model=None, plot_col='T (degC)', max_subplots=3):
inputs, labels = self.example
plt.figure(figsize=(12, 8))
plot_col_index = self.column_indices[plot_col]
max_n = min(max_subplots, len(inputs))
for n in range(max_n):
plt.subplot(max_n, 1, n+1)
plt.ylabel(f'{plot_col} [normed]')
plt.plot(self.input_indices, inputs[n, :, plot_col_index],
label='Inputs', marker='.', zorder=-10)
if self.label_columns:
label_col_index = self.label_columns_indices.get(plot_col, None)
else:
label_col_index = plot_col_index
if label_col_index is None:
continue
plt.scatter(self.label_indices, labels[n, :, label_col_index],
edgecolors='k', label='Labels', c='#2ca02c', s=64)
if model is not None:
predictions = model(inputs)
plt.scatter(self.label_indices, predictions[n, :, label_col_index],
marker='X', edgecolors='k', label='Predictions',
c='#ff7f0e', s=64)
if n == 0:
plt.legend()
plt.xlabel('Time [h]')
WindowGenerator.plot = plot
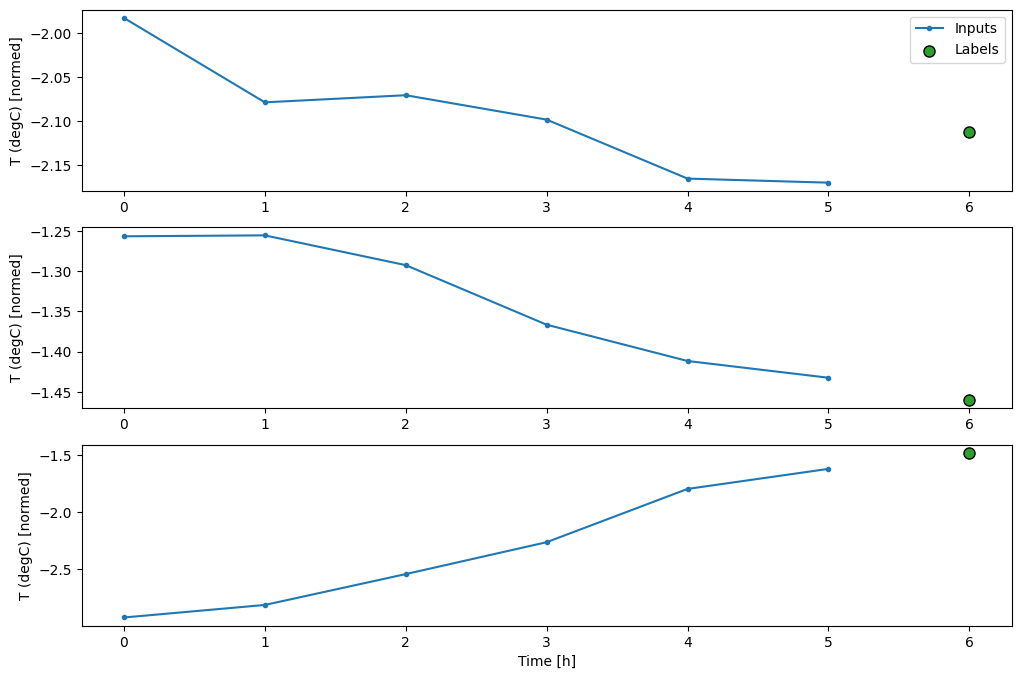
This plot aligns inputs, labels, and (later) predictions based on the time that the item refers to:
w2.plot()
You can plot the other columns, but the example window w2 configuration only has labels for the T (degC) column.
w2.plot(plot_col='p (mbar)')
4. Create tf.data.Datasets
Finally, this make_dataset method will take a time series DataFrame and convert it to a tf.data.Dataset of (input_window, label_window) pairs using the tf.keras.utils.timeseries_dataset_from_array function:
def make_dataset(self, data):
data = np.array(data, dtype=np.float32)
ds = tf.keras.utils.timeseries_dataset_from_array(
data=data,
targets=None,
sequence_length=self.total_window_size,
sequence_stride=1,
shuffle=True,
batch_size=32,)
ds = ds.map(self.split_window)
return ds
WindowGenerator.make_dataset = make_dataset
The WindowGenerator object holds training, validation, and test data.
Add properties for accessing them as tf.data.Datasets using the make_dataset method you defined earlier. Also, add a standard example batch for easy access and plotting:
@property
def train(self):
return self.make_dataset(self.train_df)
@property
def val(self):
return self.make_dataset(self.val_df)
@property
def test(self):
return self.make_dataset(self.test_df)
@property
def example(self):
"""Get and cache an example batch of `inputs, labels` for plotting."""
result = getattr(self, '_example', None)
if result is None:
# No example batch was found, so get one from the `.train` dataset
result = next(iter(self.train))
# And cache it for next time
self._example = result
return result
WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.test = test
WindowGenerator.example = example
Now, the WindowGenerator object gives you access to the tf.data.Dataset objects, so you can easily iterate over the data.
The Dataset.element_spec property tells you the structure, data types, and shapes of the dataset elements.
# Each element is an (inputs, label) pair.
w2.train.element_spec
(TensorSpec(shape=(None, 6, 19), dtype=tf.float32, name=None), TensorSpec(shape=(None, 1, 1), dtype=tf.float32, name=None))
Iterating over a Dataset yields concrete batches:
for example_inputs, example_labels in w2.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 6, 19) Labels shape (batch, time, features): (32, 1, 1)
Single step models
The simplest model you can build on this sort of data is one that predicts a single feature's value—1 time step (one hour) into the future based only on the current conditions.
So, start by building models to predict the T (degC) value one hour into the future.
Configure a WindowGenerator object to produce these single-step (input, label) pairs:
single_step_window = WindowGenerator(
input_width=1, label_width=1, shift=1,
label_columns=['T (degC)'])
single_step_window
Total window size: 2 Input indices: [0] Label indices: [1] Label column name(s): ['T (degC)']
The window object creates tf.data.Datasets from the training, validation, and test sets, allowing you to easily iterate over batches of data.
for example_inputs, example_labels in single_step_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 1, 19) Labels shape (batch, time, features): (32, 1, 1)
Baseline
Before building a trainable model it would be good to have a performance baseline as a point for comparison with the later more complicated models.
This first task is to predict temperature one hour into the future, given the current value of all features. The current values include the current temperature.
So, start with a model that just returns the current temperature as the prediction, predicting "No change". This is a reasonable baseline since temperature changes slowly. Of course, this baseline will work less well if you make a prediction further in the future.
class Baseline(tf.keras.Model):
def __init__(self, label_index=None):
super().__init__()
self.label_index = label_index
def call(self, inputs):
if self.label_index is None:
return inputs
result = inputs[:, :, self.label_index]
return result[:, :, tf.newaxis]
Instantiate and evaluate this model:
baseline = Baseline(label_index=column_indices['T (degC)'])
baseline.compile(loss=tf.keras.losses.MeanSquaredError(),
metrics=[tf.keras.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val, return_dict=True)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0, return_dict=True)
1/439 ━━━━━━━━━━━━━━━━━━━━ 2:27 337ms/step - loss: 0.0075 - mean_absolute_error: 0.0657 WARNING: All log messages before absl::InitializeLog() is called are written to STDERR I0000 00:00:1723775844.435380 80829 service.cc:146] XLA service 0x7eff1c004a90 initialized for platform CUDA (this does not guarantee that XLA will be used). Devices: I0000 00:00:1723775844.435411 80829 service.cc:154] StreamExecutor device (0): Tesla T4, Compute Capability 7.5 I0000 00:00:1723775844.435416 80829 service.cc:154] StreamExecutor device (1): Tesla T4, Compute Capability 7.5 I0000 00:00:1723775844.435419 80829 service.cc:154] StreamExecutor device (2): Tesla T4, Compute Capability 7.5 I0000 00:00:1723775844.435422 80829 service.cc:154] StreamExecutor device (3): Tesla T4, Compute Capability 7.5 I0000 00:00:1723775844.614710 80829 device_compiler.h:188] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process. 439/439 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.0121 - mean_absolute_error: 0.0769
That printed some performance metrics, but those don't give you a feeling for how well the model is doing.
The WindowGenerator has a plot method, but the plots won't be very interesting with only a single sample.
So, create a wider WindowGenerator that generates windows 24 hours of consecutive inputs and labels at a time. The new wide_window variable doesn't change the way the model operates. The model still makes predictions one hour into the future based on a single input time step. Here, the time axis acts like the batch axis: each prediction is made independently with no interaction between time steps:
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1,
label_columns=['T (degC)'])
wide_window
Total window size: 25 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] Label column name(s): ['T (degC)']
This expanded window can be passed directly to the same baseline model without any code changes. This is possible because the inputs and labels have the same number of time steps, and the baseline just forwards the input to the output:
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
By plotting the baseline model's predictions, notice that it is simply the labels shifted right by one hour:
wide_window.plot(baseline)
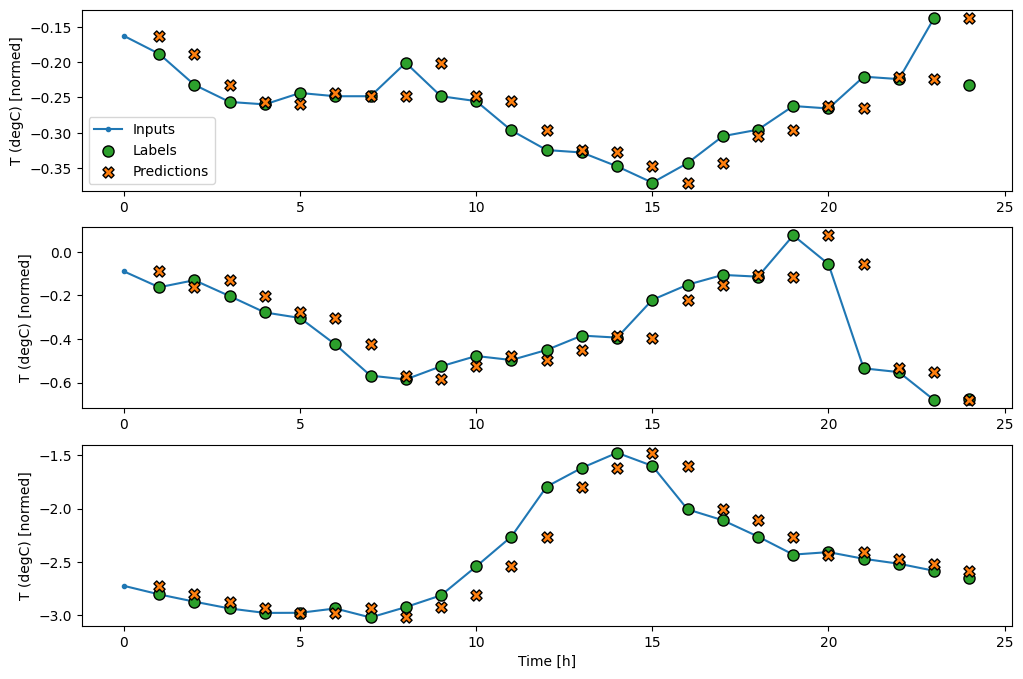
In the above plots of three examples the single step model is run over the course of 24 hours. This deserves some explanation:
- The blue
Inputsline shows the input temperature at each time step. The model receives all features, this plot only shows the temperature. - The green
Labelsdots show the target prediction value. These dots are shown at the prediction time, not the input time. That is why the range of labels is shifted 1 step relative to the inputs. - The orange
Predictionscrosses are the model's prediction's for each output time step. If the model were predicting perfectly the predictions would land directly on theLabels.
Linear model
The simplest trainable model you can apply to this task is to insert linear transformation between the input and output. In this case the output from a time step only depends on that step:

A tf.keras.layers.Dense layer with no activation set is a linear model. The layer only transforms the last axis of the data from (batch, time, inputs) to (batch, time, units); it is applied independently to every item across the batch and time axes.
linear = tf.keras.Sequential([
tf.keras.layers.Dense(units=1)
])
print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)
Input shape: (32, 1, 19) Output shape: (32, 1, 1)
This tutorial trains many models, so package the training procedure into a function:
MAX_EPOCHS = 20
def compile_and_fit(model, window, patience=2):
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
patience=patience,
mode='min')
model.compile(loss=tf.keras.losses.MeanSquaredError(),
optimizer=tf.keras.optimizers.Adam(),
metrics=[tf.keras.metrics.MeanAbsoluteError()])
history = model.fit(window.train, epochs=MAX_EPOCHS,
validation_data=window.val,
callbacks=[early_stopping])
return history
Train the model and evaluate its performance:
history = compile_and_fit(linear, single_step_window)
val_performance['Linear'] = linear.evaluate(single_step_window.val, return_dict=True)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0, return_dict=True)
Epoch 1/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 4s 2ms/step - loss: 0.6140 - mean_absolute_error: 0.5149 - val_loss: 0.0133 - val_mean_absolute_error: 0.0868 Epoch 2/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 0.0114 - mean_absolute_error: 0.0798 - val_loss: 0.0090 - val_mean_absolute_error: 0.0699 Epoch 3/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0093 - mean_absolute_error: 0.0704 - val_loss: 0.0087 - val_mean_absolute_error: 0.0684 Epoch 4/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0091 - mean_absolute_error: 0.0696 - val_loss: 0.0087 - val_mean_absolute_error: 0.0681 Epoch 5/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0091 - mean_absolute_error: 0.0695 - val_loss: 0.0086 - val_mean_absolute_error: 0.0684 Epoch 6/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0091 - mean_absolute_error: 0.0695 - val_loss: 0.0086 - val_mean_absolute_error: 0.0683 Epoch 7/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0091 - mean_absolute_error: 0.0694 - val_loss: 0.0086 - val_mean_absolute_error: 0.0685 Epoch 8/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0091 - mean_absolute_error: 0.0694 - val_loss: 0.0086 - val_mean_absolute_error: 0.0681 Epoch 9/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0091 - mean_absolute_error: 0.0694 - val_loss: 0.0087 - val_mean_absolute_error: 0.0687 439/439 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.0087 - mean_absolute_error: 0.0680
Like the baseline model, the linear model can be called on batches of wide windows. Used this way the model makes a set of independent predictions on consecutive time steps. The time axis acts like another batch axis. There are no interactions between the predictions at each time step.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', linear(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
Here is the plot of its example predictions on the wide_window, note how in many cases the prediction is clearly better than just returning the input temperature, but in a few cases it's worse:
wide_window.plot(linear)

One advantage to linear models is that they're relatively simple to interpret. You can pull out the layer's weights and visualize the weight assigned to each input:
plt.bar(x = range(len(train_df.columns)),
height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)
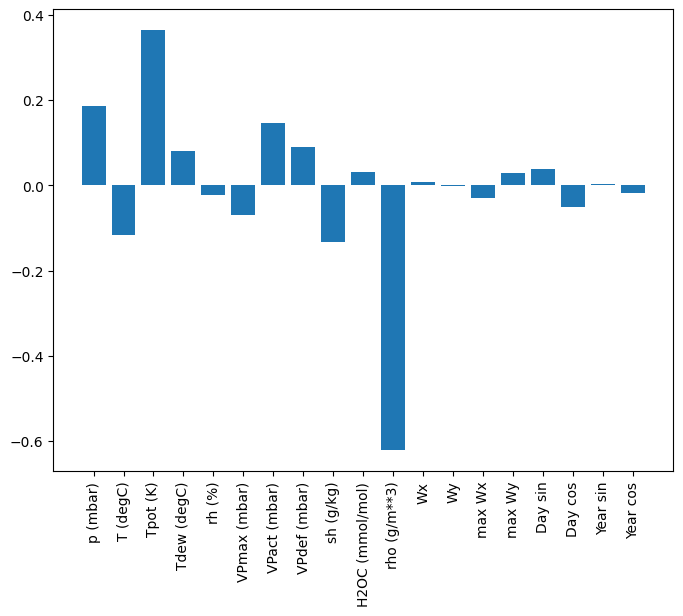
Sometimes the model doesn't even place the most weight on the input T (degC). This is one of the risks of random initialization.
Dense
Before applying models that actually operate on multiple time-steps, it's worth checking the performance of deeper, more powerful, single input step models.
Here's a model similar to the linear model, except it stacks several a few Dense layers between the input and the output:
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=1)
])
history = compile_and_fit(dense, single_step_window)
val_performance['Dense'] = dense.evaluate(single_step_window.val, return_dict=True)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0, return_dict=True)
Epoch 1/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 5s 2ms/step - loss: 0.0476 - mean_absolute_error: 0.1151 - val_loss: 0.0084 - val_mean_absolute_error: 0.0669 Epoch 2/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0081 - mean_absolute_error: 0.0650 - val_loss: 0.0071 - val_mean_absolute_error: 0.0604 Epoch 3/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0075 - mean_absolute_error: 0.0619 - val_loss: 0.0071 - val_mean_absolute_error: 0.0611 Epoch 4/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0072 - mean_absolute_error: 0.0606 - val_loss: 0.0066 - val_mean_absolute_error: 0.0564 Epoch 5/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0071 - mean_absolute_error: 0.0596 - val_loss: 0.0065 - val_mean_absolute_error: 0.0561 Epoch 6/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0069 - mean_absolute_error: 0.0587 - val_loss: 0.0065 - val_mean_absolute_error: 0.0564 Epoch 7/20 1534/1534 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.0069 - mean_absolute_error: 0.0584 - val_loss: 0.0068 - val_mean_absolute_error: 0.0572 439/439 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.0068 - mean_absolute_error: 0.0570
Multi-step dense
A single-time-step model has no context for the current values of its inputs. It can't see how the input features are changing over time. To address this issue the model needs access to multiple time steps when making predictions:
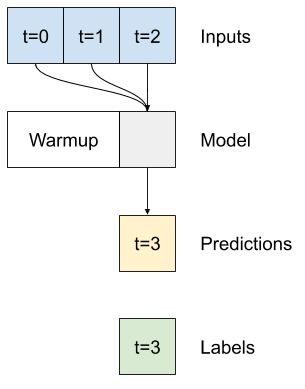
The baseline, linear and dense models handled each time step independently. Here the model will take multiple time steps as input to produce a single output.
Create a WindowGenerator that will produce batches of three-hour inputs and one-hour labels:
Note that the Window's shift parameter is relative to the end of the two windows.
CONV_WIDTH = 3
conv_window = WindowGenerator(
input_width=CONV_WIDTH,
label_width=1,
shift=1,
label_columns=['T (degC)'])
conv_window
Total window size: 4 Input indices: [0 1 2] Label indices: [3] Label column name(s): ['T (degC)']
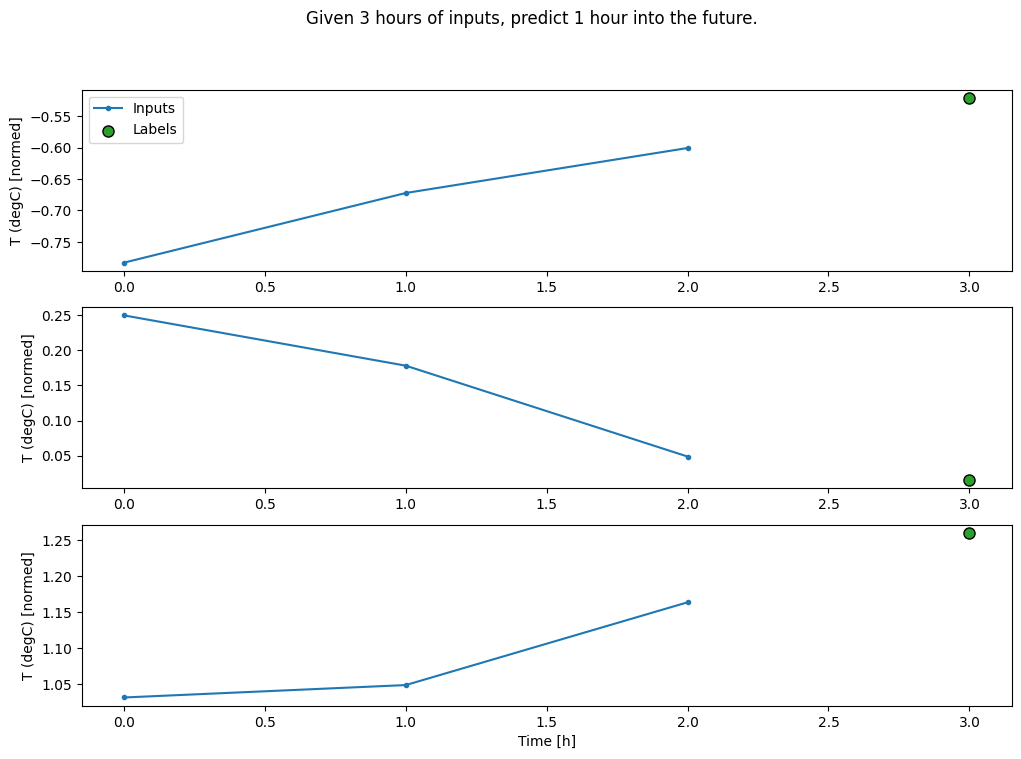
conv_window.plot()
plt.suptitle("Given 3 hours of inputs, predict 1 hour into the future.")
Text(0.5, 0.98, 'Given 3 hours of inputs, predict 1 hour into the future.')
You could train a dense model on a multiple-input-step window by adding a tf.keras.layers.Flatten as the first layer of the model:
multi_step_dense = tf.keras.Sequential([
# Shape: (time, features) => (time*features)
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
# Add back the time dimension.
# Shape: (outputs) => (1, outputs)
tf.keras.layers.Reshape([1, -1]),
])
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)
Input shape: (32, 3, 19) Output shape: (32, 1, 1)
history = compile_and_fit(multi_step_dense, conv_window)
IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val, return_dict=True)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0, return_dict=True)
438/438 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.0080 - mean_absolute_error: 0.0608
conv_window.plot(multi_step_dense)
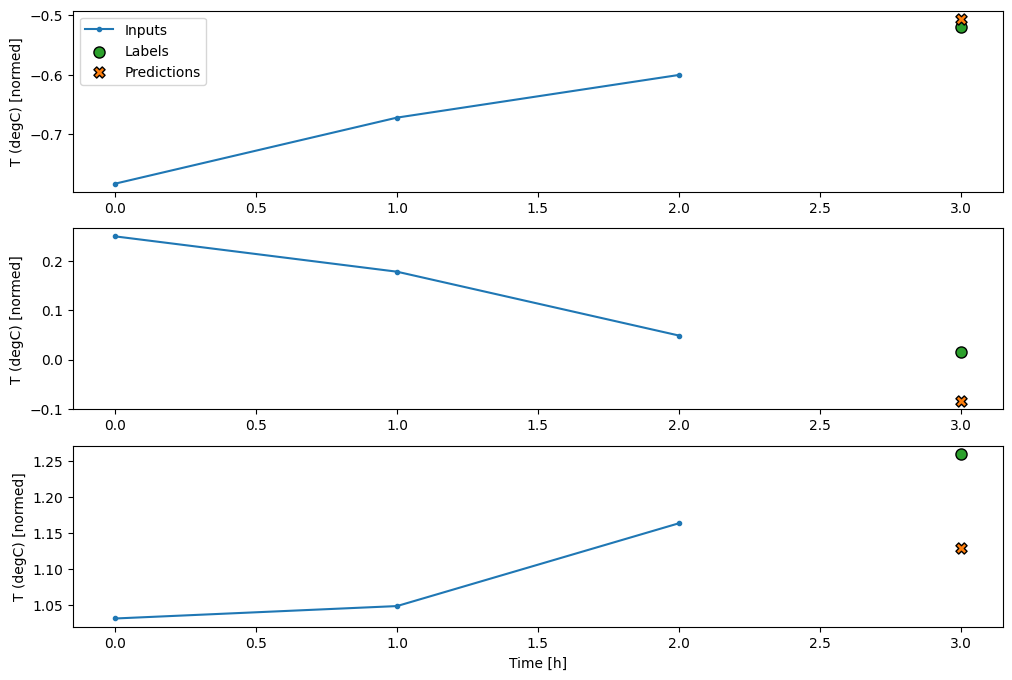
The main down-side of this approach is that the resulting model can only be executed on input windows of exactly this shape.
print('Input shape:', wide_window.example[0].shape)
try:
print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
print(f'\n{type(e).__name__}:{e}')
Input shape: (32, 24, 19) ValueError:Exception encountered when calling Sequential.call(). Input 0 of layer "dense_4" is incompatible with the layer: expected axis -1 of input shape to have value 57, but received input with shape (32, 456) Arguments received by Sequential.call(): • inputs=tf.Tensor(shape=(32, 24, 19), dtype=float32) • training=None • mask=None
The convolutional models in the next section fix this problem.
Convolution neural network
A convolution layer (tf.keras.layers.Conv1D) also takes multiple time steps as input to each prediction.
Below is the same model as multi_step_dense, re-written with a convolution.
Note the changes:
- The
tf.keras.layers.Flattenand the firsttf.keras.layers.Denseare replaced by atf.keras.layers.Conv1D. - The
tf.keras.layers.Reshapeis no longer necessary since the convolution keeps the time axis in its output.
conv_model = tf.keras.Sequential([
tf.keras.layers.Conv1D(filters=32,
kernel_size=(CONV_WIDTH,),
activation='relu'),
tf.keras.layers.Dense(units=32, activation='relu'),
tf.keras.layers.Dense(units=1),
])
Run it on an example batch to check that the model produces outputs with the expected shape:
print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)
Conv model on `conv_window` Input shape: (32, 3, 19) Output shape: (32, 1, 1)
Train and evaluate it on the conv_window and it should give performance similar to the multi_step_dense model.
history = compile_and_fit(conv_model, conv_window)
IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val, return_dict=True)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0, return_dict=True)
438/438 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.0059 - mean_absolute_error: 0.0540
The difference between this conv_model and the multi_step_dense model is that the conv_model can be run on inputs of any length. The convolutional layer is applied to a sliding window of inputs:
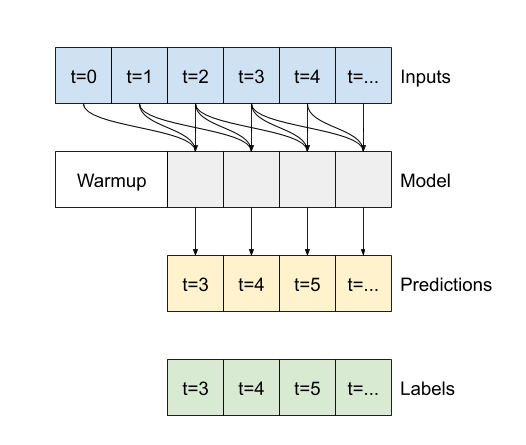
If you run it on wider input, it produces wider output:
print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)
Wide window Input shape: (32, 24, 19) Labels shape: (32, 24, 1) Output shape: (32, 22, 1) W0000 00:00:1723775965.411205 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.430143 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.431321 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.432466 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.433586 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.434754 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.435894 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.437041 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.438188 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.439356 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.440494 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.441646 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.442802 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.443962 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.459825 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced
Note that the output is shorter than the input. To make training or plotting work, you need the labels, and prediction to have the same length. So build a WindowGenerator to produce wide windows with a few extra input time steps so the label and prediction lengths match:
LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
input_width=INPUT_WIDTH,
label_width=LABEL_WIDTH,
shift=1,
label_columns=['T (degC)'])
wide_conv_window
Total window size: 27 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25] Label indices: [ 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26] Label column name(s): ['T (degC)']
print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)
Wide conv window Input shape: (32, 26, 19) Labels shape: (32, 24, 1) Output shape: (32, 24, 1) W0000 00:00:1723775965.630979 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.632244 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.633402 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.634575 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.635713 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.636852 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.637993 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.639168 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.640323 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.641462 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.642607 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.643764 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.644903 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.646054 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced W0000 00:00:1723775965.647249 80658 gpu_timer.cc:114] Skipping the delay kernel, measurement accuracy will be reduced
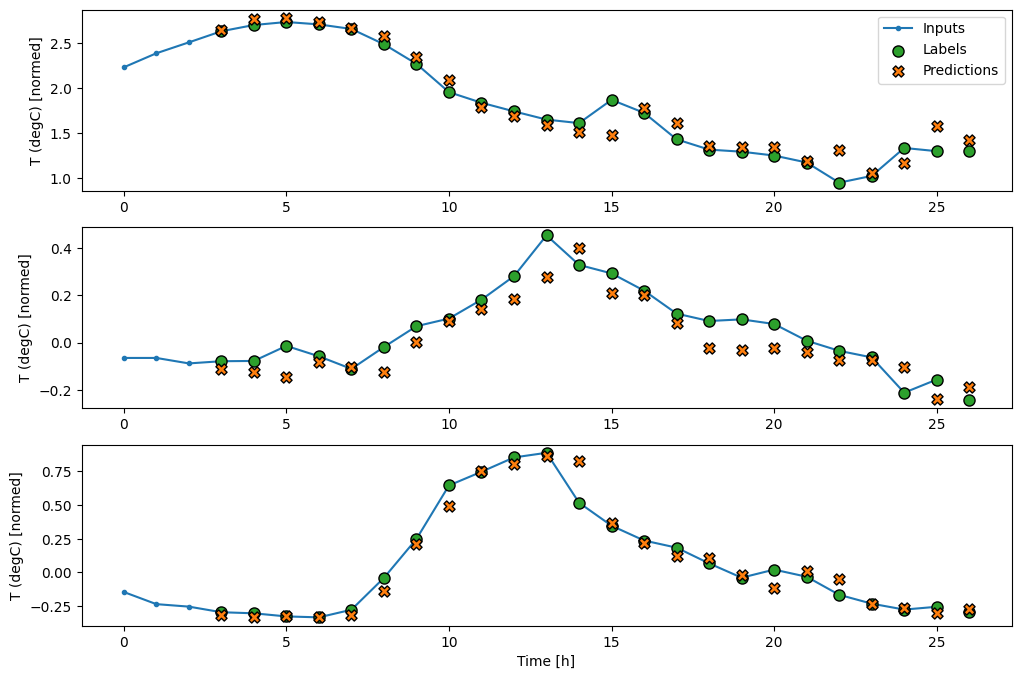
Now, you can plot the model's predictions on a wider window. Note the 3 input time steps before the first prediction. Every prediction here is based on the 3 preceding time steps:
wide_conv_window.plot(conv_model)
Recurrent neural network
A Recurrent Neural Network (RNN) is a type of neural network well-suited to time series data. RNNs process a time series step-by-step, maintaining an internal state from time-step to time-step.
You can learn more in the Text generation with an RNN tutorial and the Recurrent Neural Networks (RNN) with Keras guide.
In this tutorial, you will use an RNN layer called Long Short-Term Memory (tf.keras.layers.LSTM).
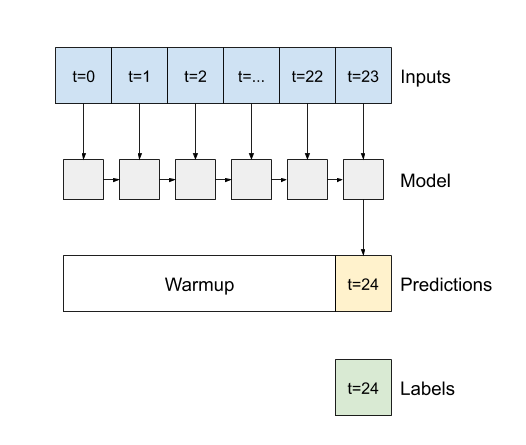
An important constructor argument for all Keras RNN layers, such as tf.keras.layers.LSTM, is the return_sequences argument. This setting can configure the layer in one of two ways:
- If
False, the default, the layer only returns the output of the final time step, giving the model time to warm up its internal state before making a single prediction:
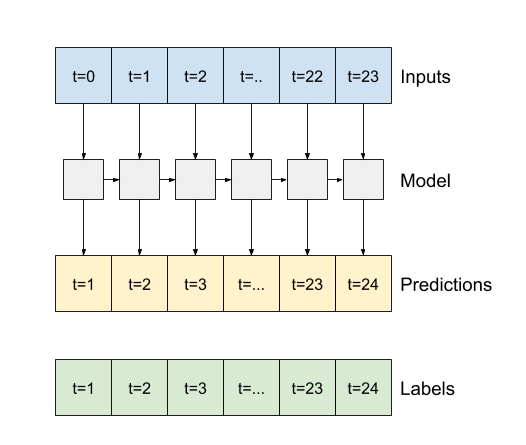
- If
True, the layer returns an output for each input. This is useful for:- Stacking RNN layers.
- Training a model on multiple time steps simultaneously.
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=1)
])
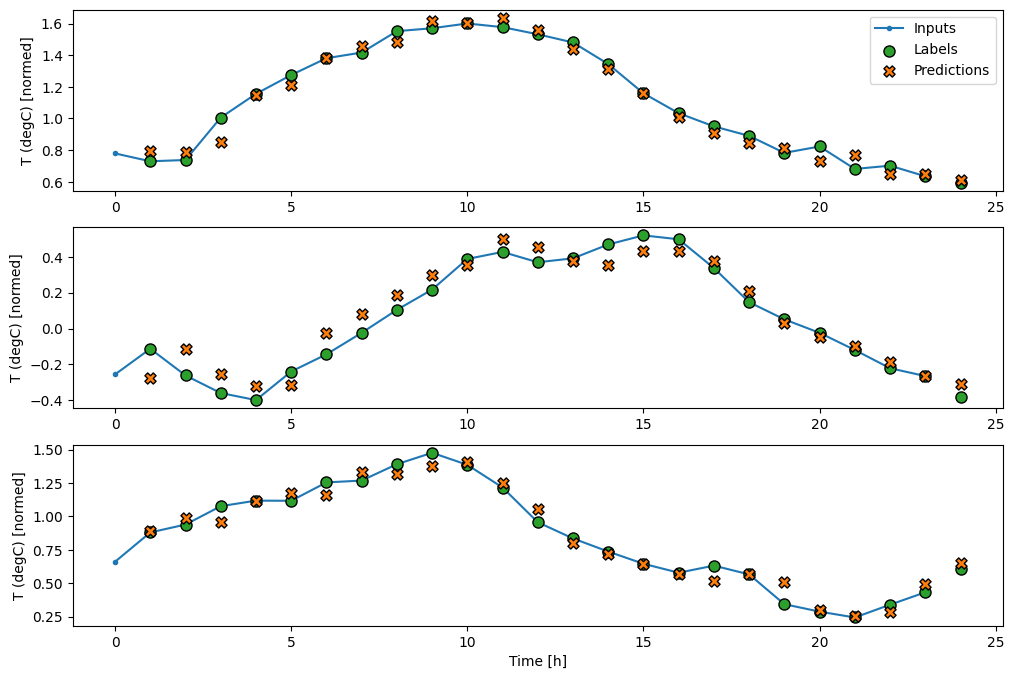
With return_sequences=True, the model can be trained on 24 hours of data at a time.
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)
Input shape: (32, 24, 19) Output shape: (32, 24, 1)
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val, return_dict=True)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0, return_dict=True)
438/438 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - loss: 0.0057 - mean_absolute_error: 0.0524
wide_window.plot(lstm_model)
Performance
With this dataset typically each of the models does slightly better than the one before it:
cm = lstm_model.metrics[1]
cm.metrics
[<MeanAbsoluteError name=mean_absolute_error>]
val_performance
{'Baseline': {'loss': 0.012845644727349281,
'mean_absolute_error': 0.07846628874540329},
'Linear': {'loss': 0.008695926517248154,
'mean_absolute_error': 0.06866316497325897},
'Dense': {'loss': 0.006793886888772249,
'mean_absolute_error': 0.05716359242796898},
'Multi step dense': {'loss': 0.007616413291543722,
'mean_absolute_error': 0.06059327721595764},
'Conv': {'loss': 0.006222909316420555,
'mean_absolute_error': 0.05451442673802376},
'LSTM': {'loss': 0.0056776562705636024,
'mean_absolute_error': 0.05233458802103996} }
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
val_mae = [v[metric_name] for v in val_performance.values()]
test_mae = [v[metric_name] for v in performance.values()]
plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
_ = plt.legend()
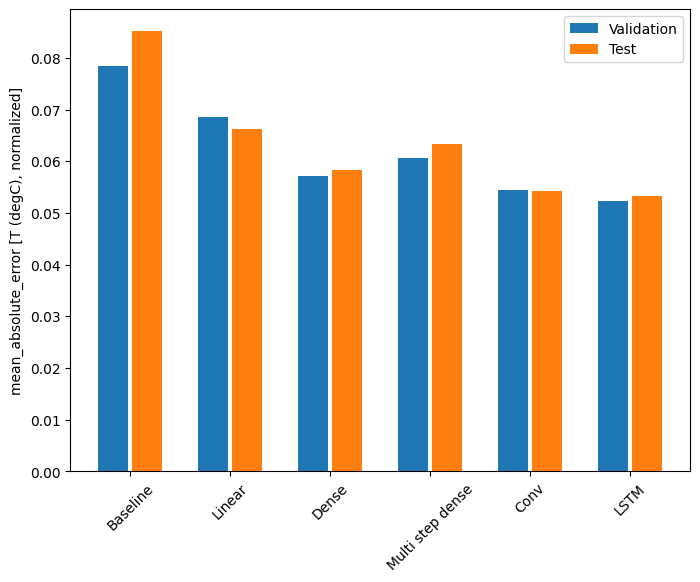
for name, value in performance.items():
print(f'{name:12s}: {value[metric_name]:0.4f}')
Baseline : 0.0852 Linear : 0.0663 Dense : 0.0584 Multi step dense: 0.0633 Conv : 0.0543 LSTM : 0.0533
Multi-output models
The models so far all predicted a single output feature, T (degC), for a single time step.
All of these models can be converted to predict multiple features just by changing the number of units in the output layer and adjusting the training windows to include all features in the labels (example_labels):
single_step_window = WindowGenerator(
# `WindowGenerator` returns all features as labels if you
# don't set the `label_columns` argument.
input_width=1, label_width=1, shift=1)
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
for example_inputs, example_labels in wide_window.train.take(1):
print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
print(f'Labels shape (batch, time, features): {example_labels.shape}')
Inputs shape (batch, time, features): (32, 24, 19) Labels shape (batch, time, features): (32, 24, 19)
Note above that the features axis of the labels now has the same depth as the inputs, instead of 1.
Baseline
The same baseline model (Baseline) can be used here, but this time repeating all features instead of selecting a specific label_index:
baseline = Baseline()
baseline.compile(loss=tf.keras.losses.MeanSquaredError(),
metrics=[tf.keras.metrics.MeanAbsoluteError()])
val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val, return_dict=True)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0, return_dict=True)
438/438 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.0885 - mean_absolute_error: 0.1591
Dense
dense = tf.keras.Sequential([
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(dense, single_step_window)
IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val, return_dict=True)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0, return_dict=True)
439/439 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.0684 - mean_absolute_error: 0.1312
RNN
%%time
wide_window = WindowGenerator(
input_width=24, label_width=24, shift=1)
lstm_model = tf.keras.models.Sequential([
# Shape [batch, time, features] => [batch, time, lstm_units]
tf.keras.layers.LSTM(32, return_sequences=True),
# Shape => [batch, time, features]
tf.keras.layers.Dense(units=num_features)
])
history = compile_and_fit(lstm_model, wide_window)
IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val, return_dict=True)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0, return_dict=True)
print()
438/438 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - loss: 0.0612 - mean_absolute_error: 0.1196 CPU times: user 4min 33s, sys: 51.8 s, total: 5min 25s Wall time: 1min 57s
Advanced: Residual connections
The Baseline model from earlier took advantage of the fact that the sequence doesn't change drastically from time step to time step. Every model trained in this tutorial so far was randomly initialized, and then had to learn that the output is a a small change from the previous time step.
While you can get around this issue with careful initialization, it's simpler to build this into the model structure.
It's common in time series analysis to build models that instead of predicting the next value, predict how the value will change in the next time step. Similarly, residual networks—or ResNets—in deep learning refer to architectures where each layer adds to the model's accumulating result.
That is how you take advantage of the knowledge that the change should be small.
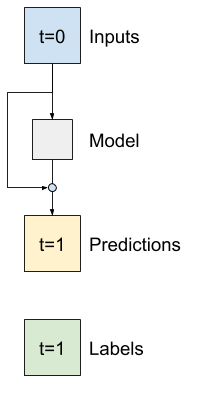
Essentially, this initializes the model to match the Baseline. For this task it helps models converge faster, with slightly better performance.
This approach can be used in conjunction with any model discussed in this tutorial.
Here, it is being applied to the LSTM model, note the use of the tf.initializers.zeros to ensure that the initial predicted changes are small, and don't overpower the residual connection. There are no symmetry-breaking concerns for the gradients here, since the zeros are only used on the last layer.
class ResidualWrapper(tf.keras.Model):
def __init__(self, model):
super().__init__()
self.model = model
def call(self, inputs, *args, **kwargs):
delta = self.model(inputs, *args, **kwargs)
# The prediction for each time step is the input
# from the previous time step plus the delta
# calculated by the model.
return inputs + delta
%%time
residual_lstm = ResidualWrapper(
tf.keras.Sequential([
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(
num_features,
# The predicted deltas should start small.
# Therefore, initialize the output layer with zeros.
kernel_initializer=tf.initializers.zeros())
]))
history = compile_and_fit(residual_lstm, wide_window)
IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val, return_dict=True)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0, return_dict=True)
print()
438/438 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - loss: 0.0622 - mean_absolute_error: 0.1184 CPU times: user 1min 40s, sys: 19.1 s, total: 1min 59s Wall time: 43.8 s
Performance
Here is the overall performance for these multi-output models.
x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
val_mae = [v[metric_name] for v in val_performance.values()]
test_mae = [v[metric_name] for v in performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()
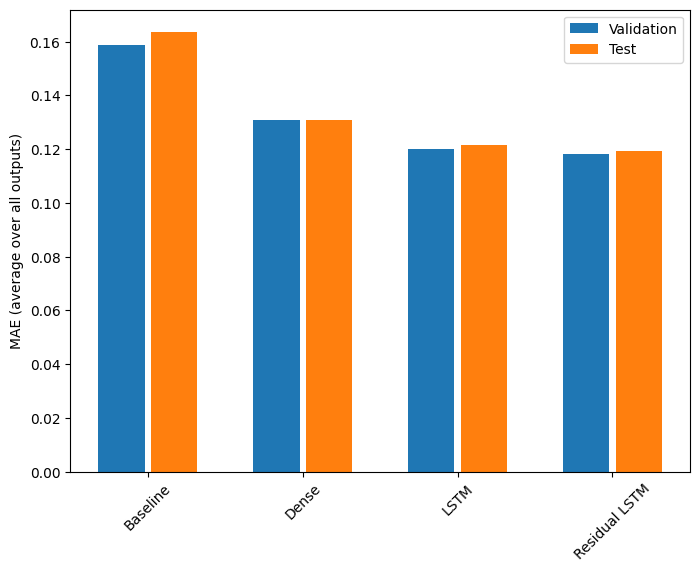
for name, value in performance.items():
print(f'{name:15s}: {value[metric_name]:0.4f}')
Baseline : 0.1638 Dense : 0.1308 LSTM : 0.1215 Residual LSTM : 0.1193
The above performances are averaged across all model outputs.
Multi-step models
Both the single-output and multiple-output models in the previous sections made single time step predictions, one hour into the future.
This section looks at how to expand these models to make multiple time step predictions.
In a multi-step prediction, the model needs to learn to predict a range of future values. Thus, unlike a single step model, where only a single future point is predicted, a multi-step model predicts a sequence of the future values.
There are two rough approaches to this:
- Single shot predictions where the entire time series is predicted at once.
- Autoregressive predictions where the model only makes single step predictions and its output is fed back as its input.
In this section all the models will predict all the features across all output time steps.
For the multi-step model, the training data again consists of hourly samples. However, here, the models will learn to predict 24 hours into the future, given 24 hours of the past.
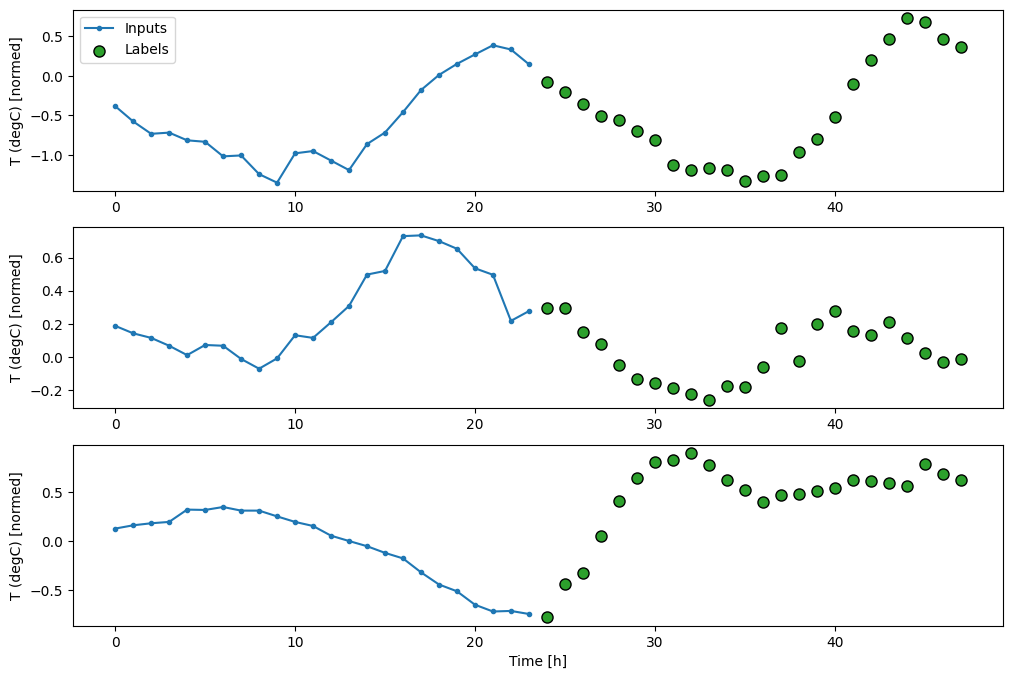
Here is a Window object that generates these slices from the dataset:
OUT_STEPS = 24
multi_window = WindowGenerator(input_width=24,
label_width=OUT_STEPS,
shift=OUT_STEPS)
multi_window.plot()
multi_window
Total window size: 48 Input indices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] Label indices: [24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] Label column name(s): None
Baselines
A simple baseline for this task is to repeat the last input time step for the required number of output time steps:
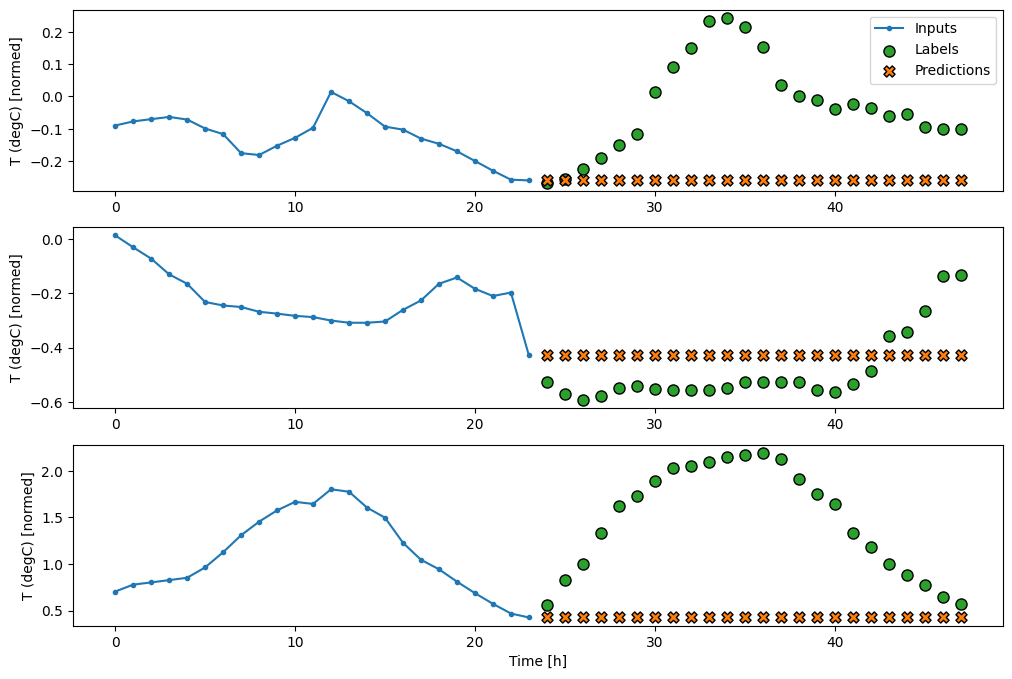
class MultiStepLastBaseline(tf.keras.Model):
def call(self, inputs):
return tf.tile(inputs[:, -1:, :], [1, OUT_STEPS, 1])
last_baseline = MultiStepLastBaseline()
last_baseline.compile(loss=tf.keras.losses.MeanSquaredError(),
metrics=[tf.keras.metrics.MeanAbsoluteError()])
multi_val_performance = {}
multi_performance = {}
multi_val_performance['Last'] = last_baseline.evaluate(multi_window.val, return_dict=True)
multi_performance['Last'] = last_baseline.evaluate(multi_window.test, verbose=0, return_dict=True)
multi_window.plot(last_baseline)
437/437 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.6271 - mean_absolute_error: 0.4992
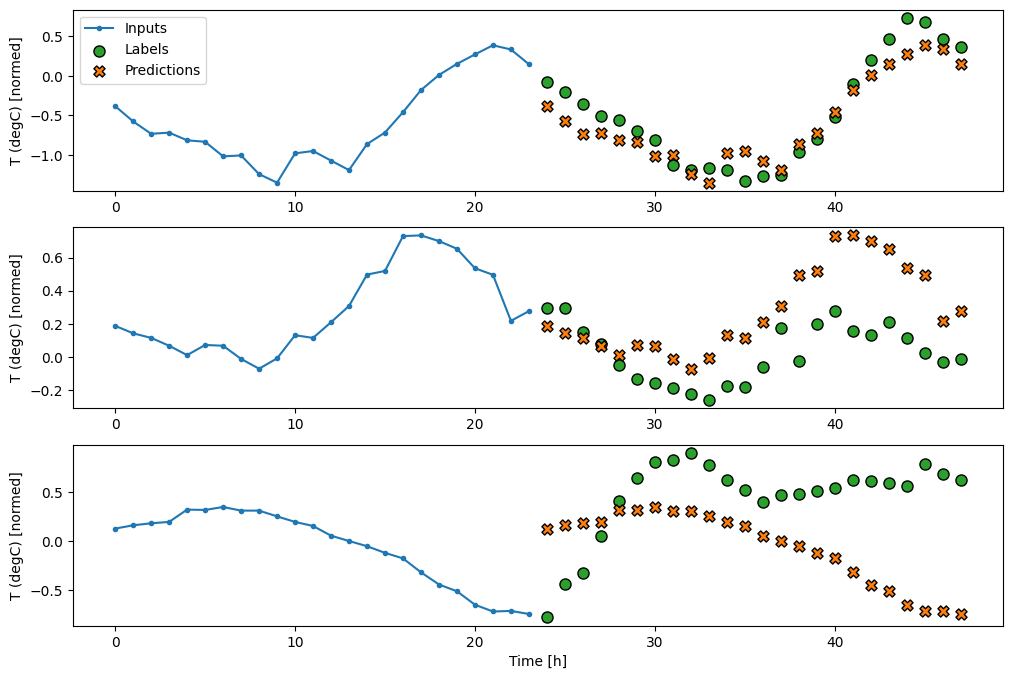
Since this task is to predict 24 hours into the future, given 24 hours of the past, another simple approach is to repeat the previous day, assuming tomorrow will be similar:
class RepeatBaseline(tf.keras.Model):
def call(self, inputs):
return inputs
repeat_baseline = RepeatBaseline()
repeat_baseline.compile(loss=tf.keras.losses.MeanSquaredError(),
metrics=[tf.keras.metrics.MeanAbsoluteError()])
multi_val_performance['Repeat'] = repeat_baseline.evaluate(multi_window.val, return_dict=True)
multi_performance['Repeat'] = repeat_baseline.evaluate(multi_window.test, verbose=0, return_dict=True)
multi_window.plot(repeat_baseline)
437/437 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.4241 - mean_absolute_error: 0.3948
Single-shot models
One high-level approach to this problem is to use a "single-shot" model, where the model makes the entire sequence prediction in a single step.
This can be implemented efficiently as a tf.keras.layers.Dense with OUT_STEPS*features output units. The model just needs to reshape that output to the required (OUTPUT_STEPS, features).
Linear
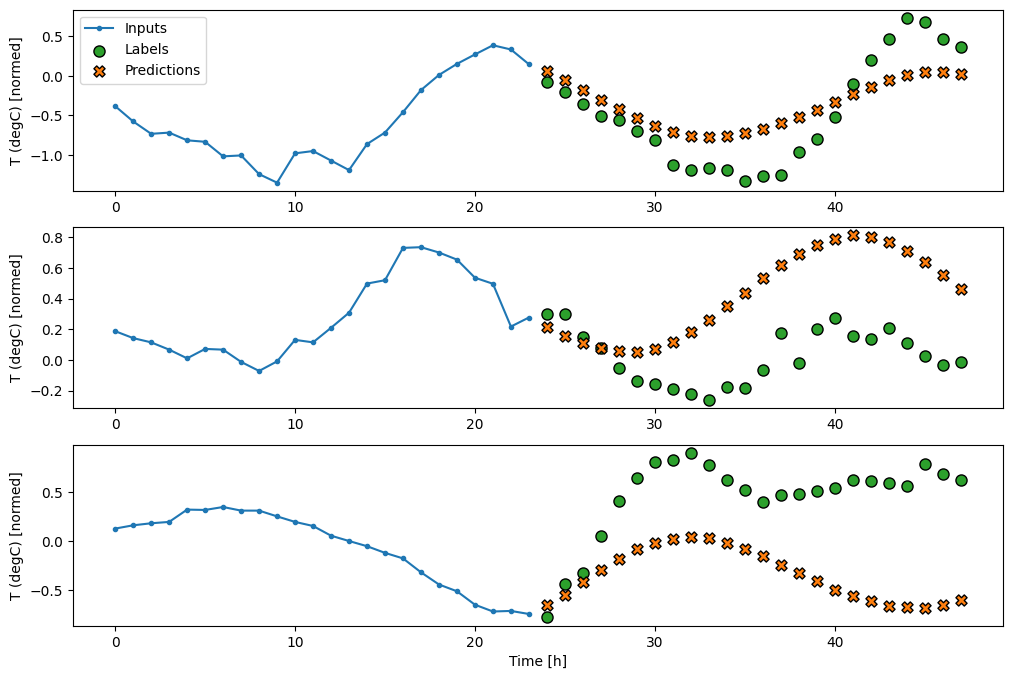
A simple linear model based on the last input time step does better than either baseline, but is underpowered. The model needs to predict OUTPUT_STEPS time steps, from a single input time step with a linear projection. It can only capture a low-dimensional slice of the behavior, likely based mainly on the time of day and time of year.
multi_linear_model = tf.keras.Sequential([
# Take the last time-step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_linear_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Linear'] = multi_linear_model.evaluate(multi_window.val, return_dict=True)
multi_performance['Linear'] = multi_linear_model.evaluate(multi_window.test, verbose=0, return_dict=True)
multi_window.plot(multi_linear_model)
437/437 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.2547 - mean_absolute_error: 0.3051
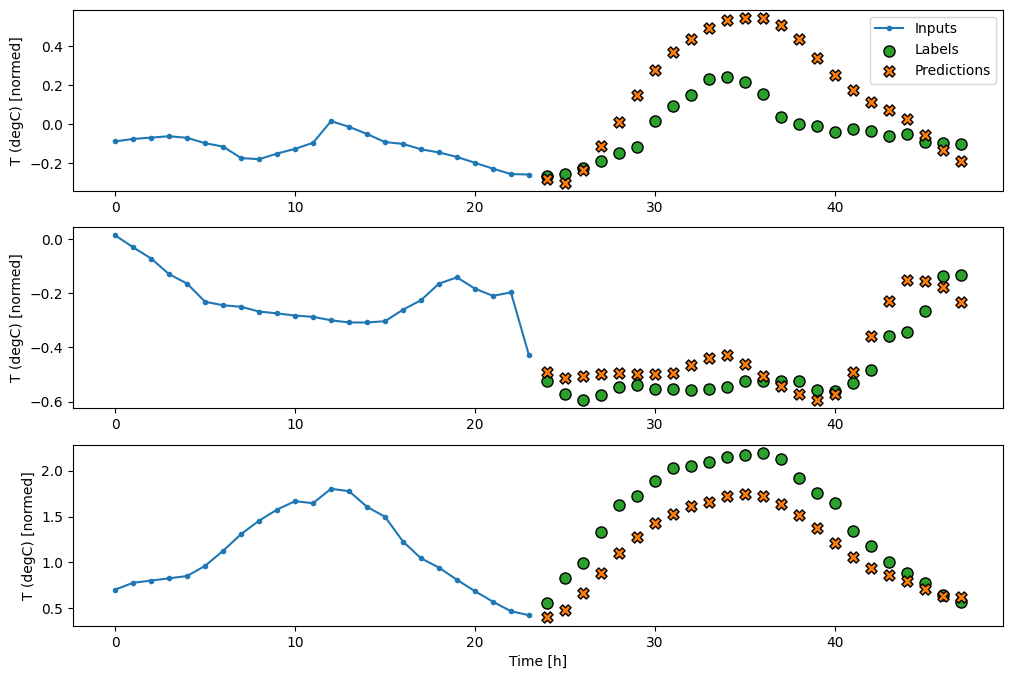
Dense
Adding a tf.keras.layers.Dense between the input and output gives the linear model more power, but is still only based on a single input time step.
multi_dense_model = tf.keras.Sequential([
# Take the last time step.
# Shape [batch, time, features] => [batch, 1, features]
tf.keras.layers.Lambda(lambda x: x[:, -1:, :]),
# Shape => [batch, 1, dense_units]
tf.keras.layers.Dense(512, activation='relu'),
# Shape => [batch, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_dense_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Dense'] = multi_dense_model.evaluate(multi_window.val, return_dict=True)
multi_performance['Dense'] = multi_dense_model.evaluate(multi_window.test, verbose=0, return_dict=True)
multi_window.plot(multi_dense_model)
437/437 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.2161 - mean_absolute_error: 0.2798
CNN
A convolutional model makes predictions based on a fixed-width history, which may lead to better performance than the dense model since it can see how things are changing over time:
CONV_WIDTH = 3
multi_conv_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, CONV_WIDTH, features]
tf.keras.layers.Lambda(lambda x: x[:, -CONV_WIDTH:, :]),
# Shape => [batch, 1, conv_units]
tf.keras.layers.Conv1D(256, activation='relu', kernel_size=(CONV_WIDTH)),
# Shape => [batch, 1, out_steps*features]
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features]
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_conv_model, multi_window)
IPython.display.clear_output()
multi_val_performance['Conv'] = multi_conv_model.evaluate(multi_window.val, return_dict=True)
multi_performance['Conv'] = multi_conv_model.evaluate(multi_window.test, verbose=0, return_dict=True)
multi_window.plot(multi_conv_model)
437/437 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - loss: 0.2133 - mean_absolute_error: 0.2794
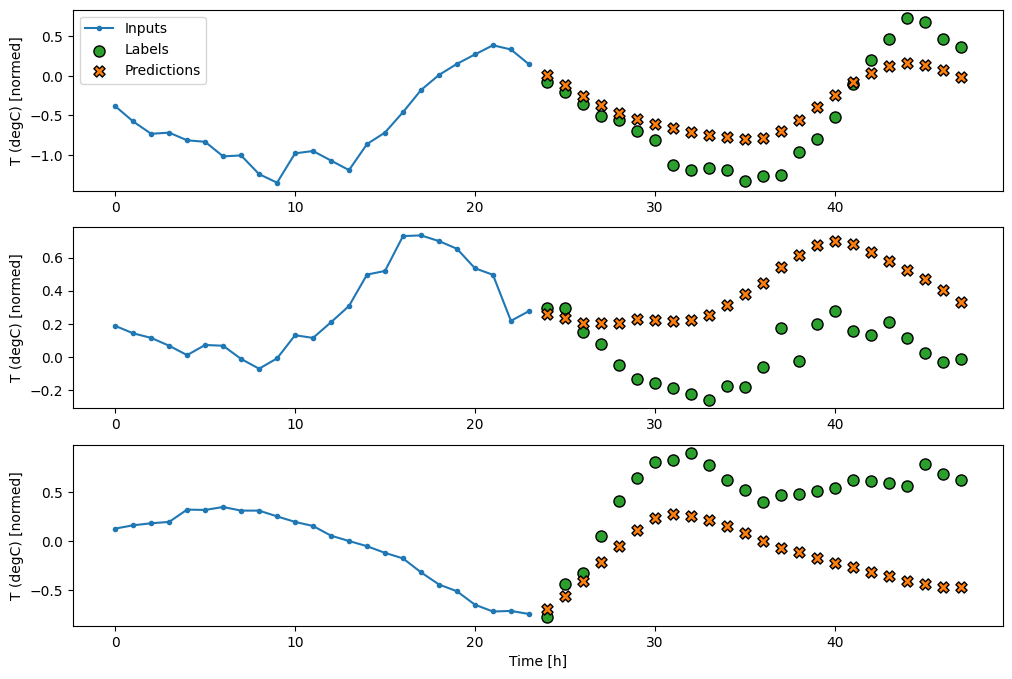
RNN
A recurrent model can learn to use a long history of inputs, if it's relevant to the predictions the model is making. Here the model will accumulate internal state for 24 hours, before making a single prediction for the next 24 hours.
In this single-shot format, the LSTM only needs to produce an output at the last time step, so set return_sequences=False in tf.keras.layers.LSTM.
multi_lstm_model = tf.keras.Sequential([
# Shape [batch, time, features] => [batch, lstm_units].
# Adding more `lstm_units` just overfits more quickly.
tf.keras.layers.LSTM(32, return_sequences=False),
# Shape => [batch, out_steps*features].
tf.keras.layers.Dense(OUT_STEPS*num_features,
kernel_initializer=tf.initializers.zeros()),
# Shape => [batch, out_steps, features].
tf.keras.layers.Reshape([OUT_STEPS, num_features])
])
history = compile_and_fit(multi_lstm_model, multi_window)
IPython.display.clear_output()
multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val, return_dict=True)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.test, verbose=0, return_dict=True)
multi_window.plot(multi_lstm_model)
437/437 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - loss: 0.2160 - mean_absolute_error: 0.2858
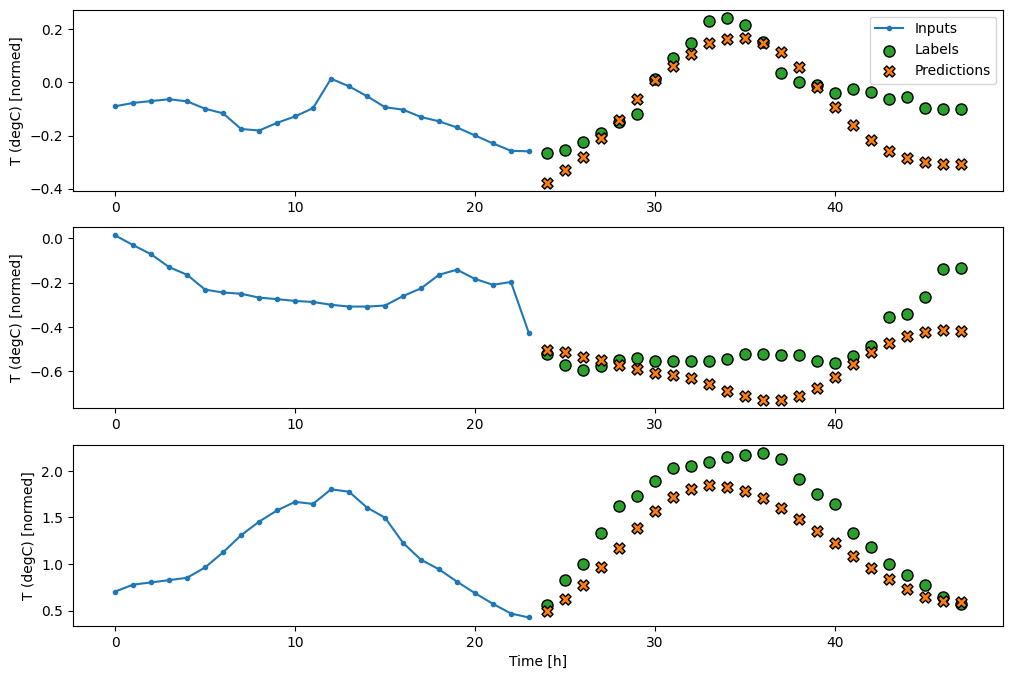
Advanced: Autoregressive model
The above models all predict the entire output sequence in a single step.
In some cases it may be helpful for the model to decompose this prediction into individual time steps. Then, each model's output can be fed back into itself at each step and predictions can be made conditioned on the previous one, like in the classic Generating Sequences With Recurrent Neural Networks.
One clear advantage to this style of model is that it can be set up to produce output with a varying length.
You could take any of the single-step multi-output models trained in the first half of this tutorial and run in an autoregressive feedback loop, but here you'll focus on building a model that's been explicitly trained to do that.
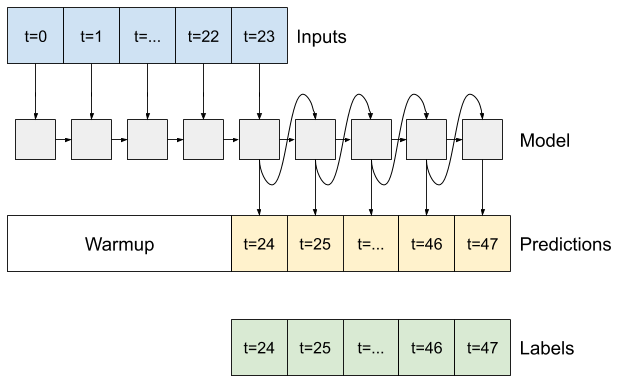
RNN
This tutorial only builds an autoregressive RNN model, but this pattern could be applied to any model that was designed to output a single time step.
The model will have the same basic form as the single-step LSTM models from earlier: a tf.keras.layers.LSTM layer followed by a tf.keras.layers.Dense layer that converts the LSTM layer's outputs to model predictions.
A tf.keras.layers.LSTM is a tf.keras.layers.LSTMCell wrapped in the higher level tf.keras.layers.RNN that manages the state and sequence results for you (Check out the Recurrent Neural Networks (RNN) with Keras guide for details).
In this case, the model has to manually manage the inputs for each step, so it uses tf.keras.layers.LSTMCell directly for the lower level, single time step interface.
class FeedBack(tf.keras.Model):
def __init__(self, units, out_steps):
super().__init__()
self.out_steps = out_steps
self.units = units
self.lstm_cell = tf.keras.layers.LSTMCell(units)
# Also wrap the LSTMCell in an RNN to simplify the `warmup` method.
self.lstm_rnn = tf.keras.layers.RNN(self.lstm_cell, return_state=True)
self.dense = tf.keras.layers.Dense(num_features)
feedback_model = FeedBack(units=32, out_steps=OUT_STEPS)
The first method this model needs is a warmup method to initialize its internal state based on the inputs. Once trained, this state will capture the relevant parts of the input history. This is equivalent to the single-step LSTM model from earlier:
def warmup(self, inputs):
# inputs.shape => (batch, time, features)
# x.shape => (batch, lstm_units)
x, *state = self.lstm_rnn(inputs)
# predictions.shape => (batch, features)
prediction = self.dense(x)
return prediction, state
FeedBack.warmup = warmup
This method returns a single time-step prediction and the internal state of the LSTM:
prediction, state = feedback_model.warmup(multi_window.example[0])
prediction.shape
TensorShape([32, 19])
With the RNN's state, and an initial prediction you can now continue iterating the model feeding the predictions at each step back as the input.
The simplest approach for collecting the output predictions is to use a Python list and a tf.stack after the loop.
def call(self, inputs, training=None):
# Use a TensorArray to capture dynamically unrolled outputs.
predictions = []
# Initialize the LSTM state.
prediction, state = self.warmup(inputs)
# Insert the first prediction.
predictions.append(prediction)
# Run the rest of the prediction steps.
for n in range(1, self.out_steps):
# Use the last prediction as input.
x = prediction
# Execute one lstm step.
x, state = self.lstm_cell(x, states=state,
training=training)
# Convert the lstm output to a prediction.
prediction = self.dense(x)
# Add the prediction to the output.
predictions.append(prediction)
# predictions.shape => (time, batch, features)
predictions = tf.stack(predictions)
# predictions.shape => (batch, time, features)
predictions = tf.transpose(predictions, [1, 0, 2])
return predictions
FeedBack.call = call
Test run this model on the example inputs:
print('Output shape (batch, time, features): ', feedback_model(multi_window.example[0]).shape)
Output shape (batch, time, features): (32, 24, 19)
Now, train the model:
history = compile_and_fit(feedback_model, multi_window)
IPython.display.clear_output()
multi_val_performance['AR LSTM'] = feedback_model.evaluate(multi_window.val, return_dict=True)
multi_performance['AR LSTM'] = feedback_model.evaluate(multi_window.test, verbose=0, return_dict=True)
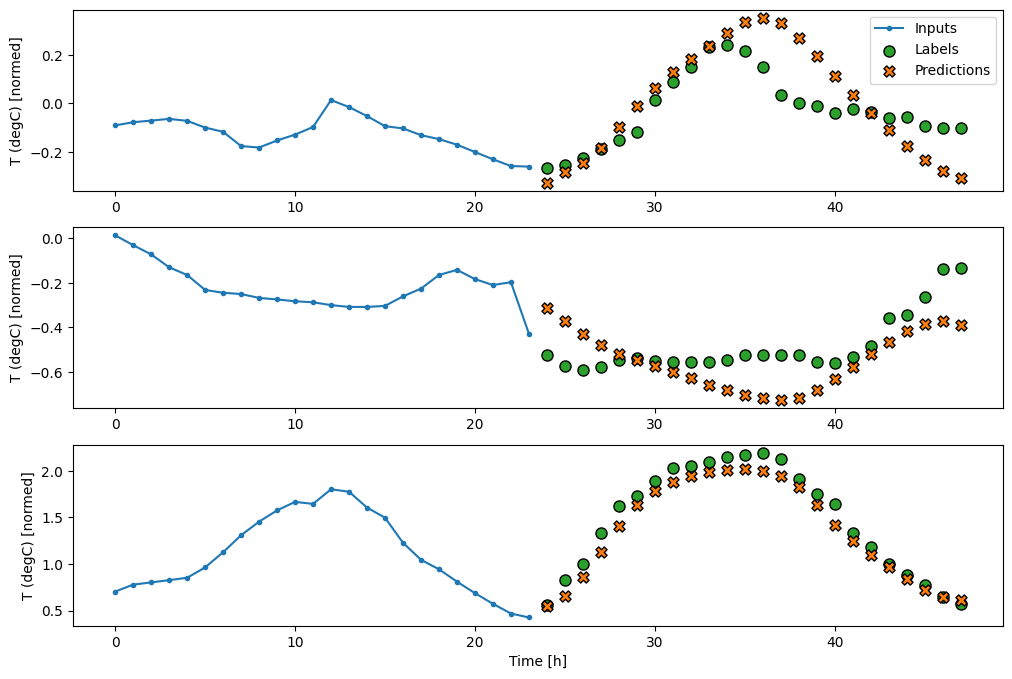
multi_window.plot(feedback_model)
437/437 ━━━━━━━━━━━━━━━━━━━━ 1s 3ms/step - loss: 0.2244 - mean_absolute_error: 0.2973
Performance
There are clearly diminishing returns as a function of model complexity on this problem:
x = np.arange(len(multi_performance))
width = 0.3
metric_name = 'mean_absolute_error'
val_mae = [v[metric_name] for v in multi_val_performance.values()]
test_mae = [v[metric_name] for v in multi_performance.values()]
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=multi_performance.keys(),
rotation=45)
plt.ylabel(f'MAE (average over all times and outputs)')
_ = plt.legend()
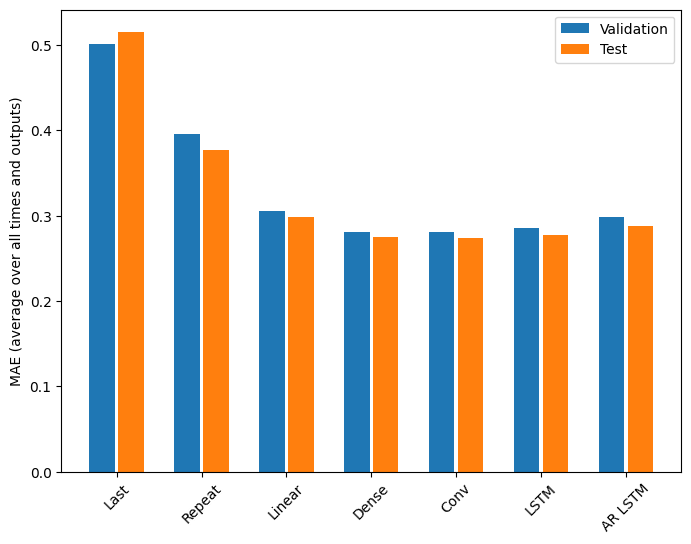
The metrics for the multi-output models in the first half of this tutorial show the performance averaged across all output features. These performances are similar but also averaged across output time steps.
for name, value in multi_performance.items():
print(f'{name:8s}: {value[metric_name]:0.4f}')
Last : 0.5157 Repeat : 0.3774 Linear : 0.2980 Dense : 0.2765 Conv : 0.2732 LSTM : 0.2767 AR LSTM : 0.2910
The gains achieved going from a dense model to convolutional and recurrent models are only a few percent (if any), and the autoregressive model performed clearly worse. So these more complex approaches may not be worth while on this problem, but there was no way to know without trying, and these models could be helpful for your problem.
Next steps
This tutorial was a quick introduction to time series forecasting using TensorFlow.
To learn more, refer to:
- Chapter 15 of Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Edition.
- Chapter 6 of Deep Learning with Python.
- Lesson 8 of Udacity's intro to TensorFlow for deep learning, including the exercise notebooks.
Also, remember that you can implement any classical time series model in TensorFlow—this tutorial just focuses on TensorFlow's built-in functionality.
