 View on TensorFlow.org
View on TensorFlow.org
|
 Run in Google Colab
Run in Google Colab
|
 View source on GitHub
View source on GitHub
|
 Download notebook Download notebook
|
Overview
This notebook shows how to do lossy data compression using neural networks and TensorFlow Compression.
Lossy compression involves making a trade-off between rate, the expected number of bits needed to encode a sample, and distortion, the expected error in the reconstruction of the sample.
The examples below use an autoencoder-like model to compress images from the MNIST dataset. The method is based on the paper End-to-end Optimized Image Compression.
More background on learned data compression can be found in this paper targeted at people familiar with classical data compression, or this survey targeted at a machine learning audience.
Setup
Install Tensorflow Compression via pip.
# Installs the latest version of TFC compatible with the installed TF version.read MAJOR MINOR <<< "$(pip show tensorflow | perl -p -0777 -e 's/.*Version: (\d+)\.(\d+).*/\1 \2/sg')"pip install "tensorflow-compression<$MAJOR.$(($MINOR+1))"
ERROR: pip's dependency resolver does not currently take into account all the packages that are installed. This behaviour is the source of the following dependency conflicts. tf-keras 2.17.0 requires tensorflow<2.18,>=2.17, but you have tensorflow 2.14.1 which is incompatible.
Import library dependencies.
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_compression as tfc
import tensorflow_datasets as tfds
2024-08-16 06:46:30.122902: E tensorflow/compiler/xla/stream_executor/cuda/cuda_dnn.cc:9342] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2024-08-16 06:46:30.122949: E tensorflow/compiler/xla/stream_executor/cuda/cuda_fft.cc:609] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2024-08-16 06:46:30.122988: E tensorflow/compiler/xla/stream_executor/cuda/cuda_blas.cc:1518] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
Define the trainer model.
Because the model resembles an autoencoder, and we need to perform a different set of functions during training and inference, the setup is a little different from, say, a classifier.
The training model consists of three parts:
- the analysis (or encoder) transform, converting from the image into a latent space,
- the synthesis (or decoder) transform, converting from the latent space back into image space, and
- a prior and entropy model, modeling the marginal probabilities of the latents.
First, define the transforms:
def make_analysis_transform(latent_dims):
"""Creates the analysis (encoder) transform."""
return tf.keras.Sequential([
tf.keras.layers.Conv2D(
20, 5, use_bias=True, strides=2, padding="same",
activation="leaky_relu", name="conv_1"),
tf.keras.layers.Conv2D(
50, 5, use_bias=True, strides=2, padding="same",
activation="leaky_relu", name="conv_2"),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(
500, use_bias=True, activation="leaky_relu", name="fc_1"),
tf.keras.layers.Dense(
latent_dims, use_bias=True, activation=None, name="fc_2"),
], name="analysis_transform")
def make_synthesis_transform():
"""Creates the synthesis (decoder) transform."""
return tf.keras.Sequential([
tf.keras.layers.Dense(
500, use_bias=True, activation="leaky_relu", name="fc_1"),
tf.keras.layers.Dense(
2450, use_bias=True, activation="leaky_relu", name="fc_2"),
tf.keras.layers.Reshape((7, 7, 50)),
tf.keras.layers.Conv2DTranspose(
20, 5, use_bias=True, strides=2, padding="same",
activation="leaky_relu", name="conv_1"),
tf.keras.layers.Conv2DTranspose(
1, 5, use_bias=True, strides=2, padding="same",
activation="leaky_relu", name="conv_2"),
], name="synthesis_transform")
The trainer holds an instance of both transforms, as well as the parameters of the prior.
Its call method is set up to compute:
- rate, an estimate of the number of bits needed to represent the batch of digits, and
- distortion, the mean absolute difference between the pixels of the original digits and their reconstructions.
class MNISTCompressionTrainer(tf.keras.Model):
"""Model that trains a compressor/decompressor for MNIST."""
def __init__(self, latent_dims):
super().__init__()
self.analysis_transform = make_analysis_transform(latent_dims)
self.synthesis_transform = make_synthesis_transform()
self.prior_log_scales = tf.Variable(tf.zeros((latent_dims,)))
@property
def prior(self):
return tfc.NoisyLogistic(loc=0., scale=tf.exp(self.prior_log_scales))
def call(self, x, training):
"""Computes rate and distortion losses."""
# Ensure inputs are floats in the range (0, 1).
x = tf.cast(x, self.compute_dtype) / 255.
x = tf.reshape(x, (-1, 28, 28, 1))
# Compute latent space representation y, perturb it and model its entropy,
# then compute the reconstructed pixel-level representation x_hat.
y = self.analysis_transform(x)
entropy_model = tfc.ContinuousBatchedEntropyModel(
self.prior, coding_rank=1, compression=False)
y_tilde, rate = entropy_model(y, training=training)
x_tilde = self.synthesis_transform(y_tilde)
# Average number of bits per MNIST digit.
rate = tf.reduce_mean(rate)
# Mean absolute difference across pixels.
distortion = tf.reduce_mean(abs(x - x_tilde))
return dict(rate=rate, distortion=distortion)
Compute rate and distortion.
Let's walk through this step by step, using one image from the training set. Load the MNIST dataset for training and validation:
training_dataset, validation_dataset = tfds.load(
"mnist",
split=["train", "test"],
shuffle_files=True,
as_supervised=True,
with_info=False,
)
2024-08-16 06:46:34.105151: W tensorflow/core/common_runtime/gpu/gpu_device.cc:2211] Cannot dlopen some GPU libraries. Please make sure the missing libraries mentioned above are installed properly if you would like to use GPU. Follow the guide at https://www.tensorflow.org/install/gpu for how to download and setup the required libraries for your platform. Skipping registering GPU devices...
And extract one image \(x\):
(x, _), = validation_dataset.take(1)
plt.imshow(tf.squeeze(x))
print(f"Data type: {x.dtype}")
print(f"Shape: {x.shape}")
Data type: <dtype: 'uint8'> Shape: (28, 28, 1) 2024-08-16 06:46:34.371046: W tensorflow/core/kernels/data/cache_dataset_ops.cc:854] The calling iterator did not fully read the dataset being cached. In order to avoid unexpected truncation of the dataset, the partially cached contents of the dataset will be discarded. This can happen if you have an input pipeline similar to `dataset.cache().take(k).repeat()`. You should use `dataset.take(k).cache().repeat()` instead.
To get the latent representation \(y\), we need to cast it to float32, add a batch dimension, and pass it through the analysis transform.
x = tf.cast(x, tf.float32) / 255.
x = tf.reshape(x, (-1, 28, 28, 1))
y = make_analysis_transform(10)(x)
print("y:", y)
y: tf.Tensor( [[-0.03515958 -0.04426444 0.02830836 -0.00623044 0.00728801 -0.01185333 -0.06493839 0.02908771 -0.05313966 -0.01150604]], shape=(1, 10), dtype=float32)
The latents will be quantized at test time. To model this in a differentiable way during training, we add uniform noise in the interval \((-.5, .5)\) and call the result \(\tilde y\). This is the same terminology as used in the paper End-to-end Optimized Image Compression.
y_tilde = y + tf.random.uniform(y.shape, -.5, .5)
print("y_tilde:", y_tilde)
y_tilde: tf.Tensor( [[ 0.23809135 -0.00584603 0.09636745 0.20950142 0.13149777 -0.12119483 -0.3411804 0.1945247 0.43893054 0.08348517]], shape=(1, 10), dtype=float32)
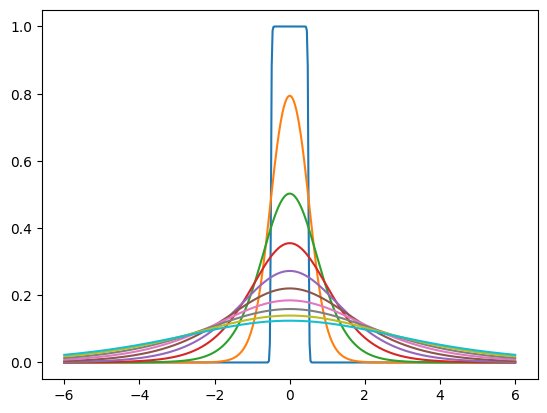
The "prior" is a probability density that we train to model the marginal distribution of the noisy latents. For example, it could be a set of independent logistic distributions with different scales for each latent dimension. tfc.NoisyLogistic accounts for the fact that the latents have additive noise. As the scale approaches zero, a logistic distribution approaches a dirac delta (spike), but the added noise causes the "noisy" distribution to approach the uniform distribution instead.
prior = tfc.NoisyLogistic(loc=0., scale=tf.linspace(.01, 2., 10))
_ = tf.linspace(-6., 6., 501)[:, None]
plt.plot(_, prior.prob(_));
During training, tfc.ContinuousBatchedEntropyModel adds uniform noise, and uses the noise and the prior to compute a (differentiable) upper bound on the rate (the average number of bits necessary to encode the latent representation). That bound can be minimized as a loss.
entropy_model = tfc.ContinuousBatchedEntropyModel(
prior, coding_rank=1, compression=False)
y_tilde, rate = entropy_model(y, training=True)
print("rate:", rate)
print("y_tilde:", y_tilde)
rate: tf.Tensor([18.123432], shape=(1,), dtype=float32) y_tilde: tf.Tensor( [[ 0.2644348 0.00915181 0.23324046 -0.40824887 0.424091 0.3612876 0.02335981 0.2968393 -0.1207529 0.05890064]], shape=(1, 10), dtype=float32)
Lastly, the noisy latents are passed back through the synthesis transform to produce an image reconstruction \(\tilde x\). Distortion is the error between original image and reconstruction. Obviously, with the transforms untrained, the reconstruction is not very useful.
x_tilde = make_synthesis_transform()(y_tilde)
# Mean absolute difference across pixels.
distortion = tf.reduce_mean(abs(x - x_tilde))
print("distortion:", distortion)
x_tilde = tf.saturate_cast(x_tilde[0] * 255, tf.uint8)
plt.imshow(tf.squeeze(x_tilde))
print(f"Data type: {x_tilde.dtype}")
print(f"Shape: {x_tilde.shape}")
distortion: tf.Tensor(0.17096801, shape=(), dtype=float32) Data type: <dtype: 'uint8'> Shape: (28, 28, 1)
For every batch of digits, calling the MNISTCompressionTrainer produces the rate and distortion as an average over that batch:
(example_batch, _), = validation_dataset.batch(32).take(1)
trainer = MNISTCompressionTrainer(10)
example_output = trainer(example_batch)
print("rate: ", example_output["rate"])
print("distortion: ", example_output["distortion"])
rate: tf.Tensor(20.296253, shape=(), dtype=float32) distortion: tf.Tensor(0.14659302, shape=(), dtype=float32) 2024-08-16 06:46:35.159201: W tensorflow/core/kernels/data/cache_dataset_ops.cc:854] The calling iterator did not fully read the dataset being cached. In order to avoid unexpected truncation of the dataset, the partially cached contents of the dataset will be discarded. This can happen if you have an input pipeline similar to `dataset.cache().take(k).repeat()`. You should use `dataset.take(k).cache().repeat()` instead.
In the next section, we set up the model to do gradient descent on these two losses.
Train the model.
We compile the trainer in a way that it optimizes the rate–distortion Lagrangian, that is, a sum of rate and distortion, where one of the terms is weighted by Lagrange parameter \(\lambda\).
This loss function affects the different parts of the model differently:
- The analysis transform is trained to produce a latent representation that achieves the desired trade-off between rate and distortion.
- The synthesis transform is trained to minimize distortion, given the latent representation.
- The parameters of the prior are trained to minimize the rate given the latent representation. This is identical to fitting the prior to the marginal distribution of latents in a maximum likelihood sense.
def pass_through_loss(_, x):
# Since rate and distortion are unsupervised, the loss doesn't need a target.
return x
def make_mnist_compression_trainer(lmbda, latent_dims=50):
trainer = MNISTCompressionTrainer(latent_dims)
trainer.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3),
# Just pass through rate and distortion as losses/metrics.
loss=dict(rate=pass_through_loss, distortion=pass_through_loss),
metrics=dict(rate=pass_through_loss, distortion=pass_through_loss),
loss_weights=dict(rate=1., distortion=lmbda),
)
return trainer
Next, train the model. The human annotations are not necessary here, since we just want to compress the images, so we drop them using a map and instead add "dummy" targets for rate and distortion.
def add_rd_targets(image, label):
# Training is unsupervised, so labels aren't necessary here. However, we
# need to add "dummy" targets for rate and distortion.
return image, dict(rate=0., distortion=0.)
def train_mnist_model(lmbda):
trainer = make_mnist_compression_trainer(lmbda)
trainer.fit(
training_dataset.map(add_rd_targets).batch(128).prefetch(8),
epochs=15,
validation_data=validation_dataset.map(add_rd_targets).batch(128).cache(),
validation_freq=1,
verbose=1,
)
return trainer
trainer = train_mnist_model(lmbda=2000)
Epoch 1/15 468/469 [============================>.] - ETA: 0s - loss: 216.8709 - distortion_loss: 0.0584 - rate_loss: 100.1461 - distortion_pass_through_loss: 0.0584 - rate_pass_through_loss: 100.1461 WARNING:absl:Computing quantization offsets using offset heuristic within a tf.function. Ideally, the offset heuristic should only be used to determine offsets once after training. Depending on the prior, estimating the offset might be computationally expensive. 469/469 [==============================] - 13s 22ms/step - loss: 216.7950 - distortion_loss: 0.0583 - rate_loss: 100.1332 - distortion_pass_through_loss: 0.0583 - rate_pass_through_loss: 100.1289 - val_loss: 176.3082 - val_distortion_loss: 0.0421 - val_rate_loss: 92.0145 - val_distortion_pass_through_loss: 0.0421 - val_rate_pass_through_loss: 92.0216 Epoch 2/15 469/469 [==============================] - 10s 20ms/step - loss: 165.3472 - distortion_loss: 0.0407 - rate_loss: 83.9473 - distortion_pass_through_loss: 0.0407 - rate_pass_through_loss: 83.9427 - val_loss: 155.3631 - val_distortion_loss: 0.0397 - val_rate_loss: 75.9290 - val_distortion_pass_through_loss: 0.0397 - val_rate_pass_through_loss: 75.9372 Epoch 3/15 469/469 [==============================] - 9s 20ms/step - loss: 150.4180 - distortion_loss: 0.0396 - rate_loss: 71.1453 - distortion_pass_through_loss: 0.0396 - rate_pass_through_loss: 71.1426 - val_loss: 144.3111 - val_distortion_loss: 0.0401 - val_rate_loss: 64.0771 - val_distortion_pass_through_loss: 0.0401 - val_rate_pass_through_loss: 64.0679 Epoch 4/15 469/469 [==============================] - 9s 20ms/step - loss: 142.1455 - distortion_loss: 0.0395 - rate_loss: 63.1692 - distortion_pass_through_loss: 0.0395 - rate_pass_through_loss: 63.1674 - val_loss: 136.5376 - val_distortion_loss: 0.0404 - val_rate_loss: 55.8161 - val_distortion_pass_through_loss: 0.0404 - val_rate_pass_through_loss: 55.8286 Epoch 5/15 469/469 [==============================] - 10s 20ms/step - loss: 136.9274 - distortion_loss: 0.0393 - rate_loss: 58.3971 - distortion_pass_through_loss: 0.0393 - rate_pass_through_loss: 58.3959 - val_loss: 131.0551 - val_distortion_loss: 0.0407 - val_rate_loss: 49.5784 - val_distortion_pass_through_loss: 0.0407 - val_rate_pass_through_loss: 49.5649 Epoch 6/15 469/469 [==============================] - 10s 20ms/step - loss: 133.3907 - distortion_loss: 0.0390 - rate_loss: 55.3780 - distortion_pass_through_loss: 0.0390 - rate_pass_through_loss: 55.3764 - val_loss: 128.4564 - val_distortion_loss: 0.0417 - val_rate_loss: 45.1091 - val_distortion_pass_through_loss: 0.0417 - val_rate_pass_through_loss: 45.0806 Epoch 7/15 469/469 [==============================] - 10s 20ms/step - loss: 130.3171 - distortion_loss: 0.0385 - rate_loss: 53.2658 - distortion_pass_through_loss: 0.0385 - rate_pass_through_loss: 53.2643 - val_loss: 124.0318 - val_distortion_loss: 0.0405 - val_rate_loss: 42.9713 - val_distortion_pass_through_loss: 0.0405 - val_rate_pass_through_loss: 42.9749 Epoch 8/15 469/469 [==============================] - 10s 20ms/step - loss: 127.8933 - distortion_loss: 0.0381 - rate_loss: 51.6005 - distortion_pass_through_loss: 0.0381 - rate_pass_through_loss: 51.5994 - val_loss: 123.1978 - val_distortion_loss: 0.0405 - val_rate_loss: 42.1649 - val_distortion_pass_through_loss: 0.0405 - val_rate_pass_through_loss: 42.1638 Epoch 9/15 469/469 [==============================] - 10s 20ms/step - loss: 125.6461 - distortion_loss: 0.0377 - rate_loss: 50.1962 - distortion_pass_through_loss: 0.0377 - rate_pass_through_loss: 50.1950 - val_loss: 120.4046 - val_distortion_loss: 0.0394 - val_rate_loss: 41.6417 - val_distortion_pass_through_loss: 0.0394 - val_rate_pass_through_loss: 41.6490 Epoch 10/15 469/469 [==============================] - 9s 20ms/step - loss: 123.5309 - distortion_loss: 0.0373 - rate_loss: 48.8519 - distortion_pass_through_loss: 0.0373 - rate_pass_through_loss: 48.8512 - val_loss: 117.5625 - val_distortion_loss: 0.0381 - val_rate_loss: 41.4515 - val_distortion_pass_through_loss: 0.0381 - val_rate_pass_through_loss: 41.4562 Epoch 11/15 469/469 [==============================] - 10s 21ms/step - loss: 121.6021 - distortion_loss: 0.0370 - rate_loss: 47.7015 - distortion_pass_through_loss: 0.0369 - rate_pass_through_loss: 47.7005 - val_loss: 115.9406 - val_distortion_loss: 0.0374 - val_rate_loss: 41.1221 - val_distortion_pass_through_loss: 0.0374 - val_rate_pass_through_loss: 41.1329 Epoch 12/15 469/469 [==============================] - 10s 20ms/step - loss: 119.9221 - distortion_loss: 0.0366 - rate_loss: 46.7678 - distortion_pass_through_loss: 0.0366 - rate_pass_through_loss: 46.7669 - val_loss: 115.2949 - val_distortion_loss: 0.0370 - val_rate_loss: 41.2657 - val_distortion_pass_through_loss: 0.0370 - val_rate_pass_through_loss: 41.2901 Epoch 13/15 469/469 [==============================] - 9s 20ms/step - loss: 118.3295 - distortion_loss: 0.0362 - rate_loss: 46.0043 - distortion_pass_through_loss: 0.0362 - rate_pass_through_loss: 46.0035 - val_loss: 114.3115 - val_distortion_loss: 0.0365 - val_rate_loss: 41.3752 - val_distortion_pass_through_loss: 0.0365 - val_rate_pass_through_loss: 41.3830 Epoch 14/15 469/469 [==============================] - 9s 20ms/step - loss: 117.2416 - distortion_loss: 0.0359 - rate_loss: 45.3939 - distortion_pass_through_loss: 0.0359 - rate_pass_through_loss: 45.3932 - val_loss: 113.1450 - val_distortion_loss: 0.0357 - val_rate_loss: 41.7618 - val_distortion_pass_through_loss: 0.0357 - val_rate_pass_through_loss: 41.7776 Epoch 15/15 469/469 [==============================] - 9s 20ms/step - loss: 116.2503 - distortion_loss: 0.0357 - rate_loss: 44.9476 - distortion_pass_through_loss: 0.0356 - rate_pass_through_loss: 44.9467 - val_loss: 112.1821 - val_distortion_loss: 0.0355 - val_rate_loss: 41.1623 - val_distortion_pass_through_loss: 0.0355 - val_rate_pass_through_loss: 41.1731
Compress some MNIST images.
For compression and decompression at test time, we split the trained model in two parts:
- The encoder side consists of the analysis transform and the entropy model.
- The decoder side consists of the synthesis transform and the same entropy model.
At test time, the latents will not have additive noise, but they will be quantized and then losslessly compressed, so we give them new names. We call them and the image reconstruction \(\hat x\) and \(\hat y\), respectively (following End-to-end Optimized Image Compression).
class MNISTCompressor(tf.keras.Model):
"""Compresses MNIST images to strings."""
def __init__(self, analysis_transform, entropy_model):
super().__init__()
self.analysis_transform = analysis_transform
self.entropy_model = entropy_model
def call(self, x):
# Ensure inputs are floats in the range (0, 1).
x = tf.cast(x, self.compute_dtype) / 255.
y = self.analysis_transform(x)
# Also return the exact information content of each digit.
_, bits = self.entropy_model(y, training=False)
return self.entropy_model.compress(y), bits
class MNISTDecompressor(tf.keras.Model):
"""Decompresses MNIST images from strings."""
def __init__(self, entropy_model, synthesis_transform):
super().__init__()
self.entropy_model = entropy_model
self.synthesis_transform = synthesis_transform
def call(self, string):
y_hat = self.entropy_model.decompress(string, ())
x_hat = self.synthesis_transform(y_hat)
# Scale and cast back to 8-bit integer.
return tf.saturate_cast(tf.round(x_hat * 255.), tf.uint8)
When instantiated with compression=True, the entropy model converts the learned prior into tables for a range coding algorithm. When calling compress(), this algorithm is invoked to convert the latent space vector into bit sequences. The length of each binary string approximates the information content of the latent (the negative log likelihood of the latent under the prior).
The entropy model for compression and decompression must be the same instance, because the range coding tables need to be exactly identical on both sides. Otherwise, decoding errors can occur.
def make_mnist_codec(trainer, **kwargs):
# The entropy model must be created with `compression=True` and the same
# instance must be shared between compressor and decompressor.
entropy_model = tfc.ContinuousBatchedEntropyModel(
trainer.prior, coding_rank=1, compression=True, **kwargs)
compressor = MNISTCompressor(trainer.analysis_transform, entropy_model)
decompressor = MNISTDecompressor(entropy_model, trainer.synthesis_transform)
return compressor, decompressor
compressor, decompressor = make_mnist_codec(trainer)
Grab 16 images from the validation dataset. You can select a different subset by changing the argument to skip.
(originals, _), = validation_dataset.batch(16).skip(3).take(1)
Compress them to strings, and keep track of each of their information content in bits.
strings, entropies = compressor(originals)
print(f"String representation of first digit in hexadecimal: 0x{strings[0].numpy().hex()}")
print(f"Number of bits actually needed to represent it: {entropies[0]:0.2f}")
String representation of first digit in hexadecimal: 0x089a8d9686 Number of bits actually needed to represent it: 37.59
Decompress the images back from the strings.
reconstructions = decompressor(strings)
Display each of the 16 original digits together with its compressed binary representation, and the reconstructed digit.
def display_digits(originals, strings, entropies, reconstructions):
"""Visualizes 16 digits together with their reconstructions."""
fig, axes = plt.subplots(4, 4, sharex=True, sharey=True, figsize=(12.5, 5))
axes = axes.ravel()
for i in range(len(axes)):
image = tf.concat([
tf.squeeze(originals[i]),
tf.zeros((28, 14), tf.uint8),
tf.squeeze(reconstructions[i]),
], 1)
axes[i].imshow(image)
axes[i].text(
.5, .5, f"→ 0x{strings[i].numpy().hex()} →\n{entropies[i]:0.2f} bits",
ha="center", va="top", color="white", fontsize="small",
transform=axes[i].transAxes)
axes[i].axis("off")
plt.subplots_adjust(wspace=0, hspace=0, left=0, right=1, bottom=0, top=1)
display_digits(originals, strings, entropies, reconstructions)

Note that the length of the encoded string differs from the information content of each digit.
This is because the range coding process works with discrete probabilities, and has a small amount of overhead. So, especially for short strings, the correspondence is only approximate. However, range coding is asymptotically optimal: in the limit, the expected bit count will approach the cross entropy (the expected information content), for which the rate term in the training model is an upper bound.
The rate–distortion trade-off
Above, the model was trained for a specific trade-off (given by lmbda=2000) between the average number of bits used to represent each digit and the incurred error in the reconstruction.
What happens when we repeat the experiment with different values?
Let's start by reducing \(\lambda\) to 500.
def train_and_visualize_model(lmbda):
trainer = train_mnist_model(lmbda=lmbda)
compressor, decompressor = make_mnist_codec(trainer)
strings, entropies = compressor(originals)
reconstructions = decompressor(strings)
display_digits(originals, strings, entropies, reconstructions)
train_and_visualize_model(lmbda=500)
Epoch 1/15 469/469 [==============================] - ETA: 0s - loss: 127.7013 - distortion_loss: 0.0703 - rate_loss: 92.5737 - distortion_pass_through_loss: 0.0702 - rate_pass_through_loss: 92.5675 WARNING:absl:Computing quantization offsets using offset heuristic within a tf.function. Ideally, the offset heuristic should only be used to determine offsets once after training. Depending on the prior, estimating the offset might be computationally expensive. 469/469 [==============================] - 12s 21ms/step - loss: 127.7013 - distortion_loss: 0.0703 - rate_loss: 92.5737 - distortion_pass_through_loss: 0.0702 - rate_pass_through_loss: 92.5675 - val_loss: 107.4871 - val_distortion_loss: 0.0552 - val_rate_loss: 79.8772 - val_distortion_pass_through_loss: 0.0552 - val_rate_pass_through_loss: 79.8765 Epoch 2/15 469/469 [==============================] - 9s 20ms/step - loss: 97.3885 - distortion_loss: 0.0541 - rate_loss: 70.3172 - distortion_pass_through_loss: 0.0541 - rate_pass_through_loss: 70.3120 - val_loss: 86.6660 - val_distortion_loss: 0.0612 - val_rate_loss: 56.0898 - val_distortion_pass_through_loss: 0.0611 - val_rate_pass_through_loss: 56.0988 Epoch 3/15 469/469 [==============================] - 9s 20ms/step - loss: 81.3244 - distortion_loss: 0.0564 - rate_loss: 53.1456 - distortion_pass_through_loss: 0.0564 - rate_pass_through_loss: 53.1418 - val_loss: 71.7392 - val_distortion_loss: 0.0673 - val_rate_loss: 38.0721 - val_distortion_pass_through_loss: 0.0673 - val_rate_pass_through_loss: 38.0759 Epoch 4/15 469/469 [==============================] - 9s 20ms/step - loss: 71.6396 - distortion_loss: 0.0595 - rate_loss: 41.9071 - distortion_pass_through_loss: 0.0595 - rate_pass_through_loss: 41.9044 - val_loss: 63.2747 - val_distortion_loss: 0.0767 - val_rate_loss: 24.9434 - val_distortion_pass_through_loss: 0.0766 - val_rate_pass_through_loss: 24.9559 Epoch 5/15 469/469 [==============================] - 9s 19ms/step - loss: 65.9924 - distortion_loss: 0.0622 - rate_loss: 34.8828 - distortion_pass_through_loss: 0.0622 - rate_pass_through_loss: 34.8815 - val_loss: 58.0754 - val_distortion_loss: 0.0797 - val_rate_loss: 18.2346 - val_distortion_pass_through_loss: 0.0797 - val_rate_pass_through_loss: 18.2361 Epoch 6/15 469/469 [==============================] - 9s 20ms/step - loss: 62.4760 - distortion_loss: 0.0643 - rate_loss: 30.3295 - distortion_pass_through_loss: 0.0643 - rate_pass_through_loss: 30.3285 - val_loss: 54.3282 - val_distortion_loss: 0.0804 - val_rate_loss: 14.1167 - val_distortion_pass_through_loss: 0.0805 - val_rate_pass_through_loss: 14.0998 Epoch 7/15 469/469 [==============================] - 9s 20ms/step - loss: 59.9234 - distortion_loss: 0.0655 - rate_loss: 27.1496 - distortion_pass_through_loss: 0.0655 - rate_pass_through_loss: 27.1490 - val_loss: 51.5607 - val_distortion_loss: 0.0785 - val_rate_loss: 12.3280 - val_distortion_pass_through_loss: 0.0785 - val_rate_pass_through_loss: 12.3260 Epoch 8/15 469/469 [==============================] - 9s 20ms/step - loss: 57.8360 - distortion_loss: 0.0662 - rate_loss: 24.7523 - distortion_pass_through_loss: 0.0662 - rate_pass_through_loss: 24.7515 - val_loss: 49.1663 - val_distortion_loss: 0.0739 - val_rate_loss: 12.2225 - val_distortion_pass_through_loss: 0.0739 - val_rate_pass_through_loss: 12.2252 Epoch 9/15 469/469 [==============================] - 9s 20ms/step - loss: 55.8557 - distortion_loss: 0.0661 - rate_loss: 22.8270 - distortion_pass_through_loss: 0.0661 - rate_pass_through_loss: 22.8269 - val_loss: 47.8735 - val_distortion_loss: 0.0703 - val_rate_loss: 12.7483 - val_distortion_pass_through_loss: 0.0703 - val_rate_pass_through_loss: 12.7435 Epoch 10/15 469/469 [==============================] - 9s 20ms/step - loss: 53.8931 - distortion_loss: 0.0653 - rate_loss: 21.2611 - distortion_pass_through_loss: 0.0653 - rate_pass_through_loss: 21.2607 - val_loss: 46.9746 - val_distortion_loss: 0.0678 - val_rate_loss: 13.0869 - val_distortion_pass_through_loss: 0.0677 - val_rate_pass_through_loss: 13.0893 Epoch 11/15 469/469 [==============================] - 9s 20ms/step - loss: 52.2135 - distortion_loss: 0.0645 - rate_loss: 19.9613 - distortion_pass_through_loss: 0.0645 - rate_pass_through_loss: 19.9613 - val_loss: 46.1504 - val_distortion_loss: 0.0649 - val_rate_loss: 13.6771 - val_distortion_pass_through_loss: 0.0649 - val_rate_pass_through_loss: 13.6784 Epoch 12/15 469/469 [==============================] - 9s 20ms/step - loss: 50.7047 - distortion_loss: 0.0635 - rate_loss: 18.9639 - distortion_pass_through_loss: 0.0635 - rate_pass_through_loss: 18.9636 - val_loss: 45.6434 - val_distortion_loss: 0.0636 - val_rate_loss: 13.8268 - val_distortion_pass_through_loss: 0.0636 - val_rate_pass_through_loss: 13.8222 Epoch 13/15 469/469 [==============================] - 9s 20ms/step - loss: 49.5375 - distortion_loss: 0.0627 - rate_loss: 18.1879 - distortion_pass_through_loss: 0.0627 - rate_pass_through_loss: 18.1875 - val_loss: 45.3913 - val_distortion_loss: 0.0623 - val_rate_loss: 14.2331 - val_distortion_pass_through_loss: 0.0623 - val_rate_pass_through_loss: 14.2288 Epoch 14/15 469/469 [==============================] - 9s 19ms/step - loss: 48.5012 - distortion_loss: 0.0617 - rate_loss: 17.6528 - distortion_pass_through_loss: 0.0617 - rate_pass_through_loss: 17.6525 - val_loss: 45.0980 - val_distortion_loss: 0.0618 - val_rate_loss: 14.1822 - val_distortion_pass_through_loss: 0.0619 - val_rate_pass_through_loss: 14.1783 Epoch 15/15 469/469 [==============================] - 9s 20ms/step - loss: 47.7803 - distortion_loss: 0.0611 - rate_loss: 17.2333 - distortion_pass_through_loss: 0.0611 - rate_pass_through_loss: 17.2331 - val_loss: 44.7918 - val_distortion_loss: 0.0601 - val_rate_loss: 14.7223 - val_distortion_pass_through_loss: 0.0602 - val_rate_pass_through_loss: 14.7139
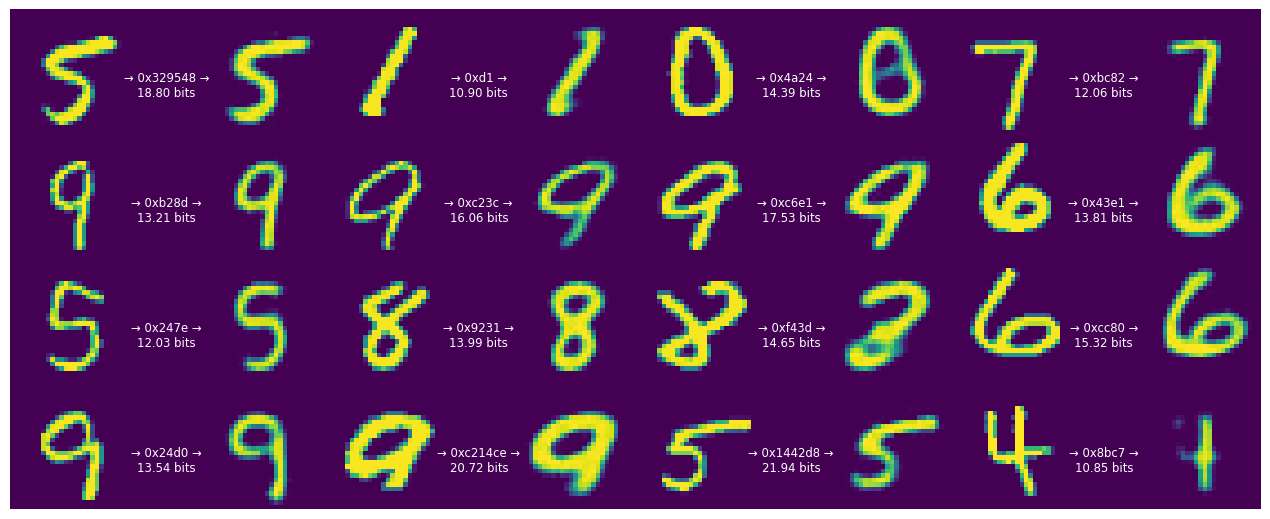
The bit rate of our code goes down, as does the fidelity of the digits. However, most of the digits remain recognizable.
Let's reduce \(\lambda\) further.
train_and_visualize_model(lmbda=300)
Epoch 1/15 469/469 [==============================] - ETA: 0s - loss: 113.5871 - distortion_loss: 0.0750 - rate_loss: 91.0911 - distortion_pass_through_loss: 0.0750 - rate_pass_through_loss: 91.0843 WARNING:absl:Computing quantization offsets using offset heuristic within a tf.function. Ideally, the offset heuristic should only be used to determine offsets once after training. Depending on the prior, estimating the offset might be computationally expensive. 469/469 [==============================] - 11s 20ms/step - loss: 113.5871 - distortion_loss: 0.0750 - rate_loss: 91.0911 - distortion_pass_through_loss: 0.0750 - rate_pass_through_loss: 91.0843 - val_loss: 96.3590 - val_distortion_loss: 0.0666 - val_rate_loss: 76.3773 - val_distortion_pass_through_loss: 0.0666 - val_rate_pass_through_loss: 76.3787 Epoch 2/15 469/469 [==============================] - 9s 20ms/step - loss: 85.8210 - distortion_loss: 0.0610 - rate_loss: 67.5072 - distortion_pass_through_loss: 0.0610 - rate_pass_through_loss: 67.5020 - val_loss: 73.8655 - val_distortion_loss: 0.0754 - val_rate_loss: 51.2544 - val_distortion_pass_through_loss: 0.0754 - val_rate_pass_through_loss: 51.2604 Epoch 3/15 469/469 [==============================] - 9s 20ms/step - loss: 68.8192 - distortion_loss: 0.0646 - rate_loss: 49.4383 - distortion_pass_through_loss: 0.0646 - rate_pass_through_loss: 49.4348 - val_loss: 58.8346 - val_distortion_loss: 0.0914 - val_rate_loss: 31.4027 - val_distortion_pass_through_loss: 0.0914 - val_rate_pass_through_loss: 31.4040 Epoch 4/15 469/469 [==============================] - 9s 20ms/step - loss: 58.2441 - distortion_loss: 0.0693 - rate_loss: 37.4659 - distortion_pass_through_loss: 0.0693 - rate_pass_through_loss: 37.4635 - val_loss: 48.4599 - val_distortion_loss: 0.0967 - val_rate_loss: 19.4409 - val_distortion_pass_through_loss: 0.0967 - val_rate_pass_through_loss: 19.4465 Epoch 5/15 469/469 [==============================] - 9s 20ms/step - loss: 51.9693 - distortion_loss: 0.0735 - rate_loss: 29.9285 - distortion_pass_through_loss: 0.0735 - rate_pass_through_loss: 29.9274 - val_loss: 42.3357 - val_distortion_loss: 0.1013 - val_rate_loss: 11.9475 - val_distortion_pass_through_loss: 0.1013 - val_rate_pass_through_loss: 11.9459 Epoch 6/15 469/469 [==============================] - 9s 20ms/step - loss: 48.0556 - distortion_loss: 0.0769 - rate_loss: 24.9786 - distortion_pass_through_loss: 0.0769 - rate_pass_through_loss: 24.9773 - val_loss: 39.0373 - val_distortion_loss: 0.1047 - val_rate_loss: 7.6218 - val_distortion_pass_through_loss: 0.1047 - val_rate_pass_through_loss: 7.6315 Epoch 7/15 469/469 [==============================] - 9s 19ms/step - loss: 45.3187 - distortion_loss: 0.0795 - rate_loss: 21.4538 - distortion_pass_through_loss: 0.0795 - rate_pass_through_loss: 21.4531 - val_loss: 36.2421 - val_distortion_loss: 0.1005 - val_rate_loss: 6.1012 - val_distortion_pass_through_loss: 0.1005 - val_rate_pass_through_loss: 6.1087 Epoch 8/15 469/469 [==============================] - 9s 20ms/step - loss: 43.1370 - distortion_loss: 0.0811 - rate_loss: 18.7982 - distortion_pass_through_loss: 0.0811 - rate_pass_through_loss: 18.7976 - val_loss: 34.1957 - val_distortion_loss: 0.0933 - val_rate_loss: 6.2151 - val_distortion_pass_through_loss: 0.0934 - val_rate_pass_through_loss: 6.2087 Epoch 9/15 469/469 [==============================] - 9s 20ms/step - loss: 41.1743 - distortion_loss: 0.0814 - rate_loss: 16.7616 - distortion_pass_through_loss: 0.0814 - rate_pass_through_loss: 16.7611 - val_loss: 33.2329 - val_distortion_loss: 0.0865 - val_rate_loss: 7.2854 - val_distortion_pass_through_loss: 0.0865 - val_rate_pass_through_loss: 7.2807 Epoch 10/15 469/469 [==============================] - 9s 20ms/step - loss: 39.4184 - distortion_loss: 0.0805 - rate_loss: 15.2631 - distortion_pass_through_loss: 0.0805 - rate_pass_through_loss: 15.2625 - val_loss: 32.7048 - val_distortion_loss: 0.0833 - val_rate_loss: 7.7035 - val_distortion_pass_through_loss: 0.0834 - val_rate_pass_through_loss: 7.7043 Epoch 11/15 469/469 [==============================] - 9s 20ms/step - loss: 37.9319 - distortion_loss: 0.0793 - rate_loss: 14.1282 - distortion_pass_through_loss: 0.0793 - rate_pass_through_loss: 14.1282 - val_loss: 32.4213 - val_distortion_loss: 0.0820 - val_rate_loss: 7.8242 - val_distortion_pass_through_loss: 0.0820 - val_rate_pass_through_loss: 7.8276 Epoch 12/15 469/469 [==============================] - 9s 20ms/step - loss: 36.7734 - distortion_loss: 0.0783 - rate_loss: 13.2686 - distortion_pass_through_loss: 0.0783 - rate_pass_through_loss: 13.2680 - val_loss: 32.1318 - val_distortion_loss: 0.0808 - val_rate_loss: 7.8993 - val_distortion_pass_through_loss: 0.0808 - val_rate_pass_through_loss: 7.9013 Epoch 13/15 469/469 [==============================] - 9s 20ms/step - loss: 35.7413 - distortion_loss: 0.0772 - rate_loss: 12.5748 - distortion_pass_through_loss: 0.0772 - rate_pass_through_loss: 12.5750 - val_loss: 31.8718 - val_distortion_loss: 0.0788 - val_rate_loss: 8.2290 - val_distortion_pass_through_loss: 0.0789 - val_rate_pass_through_loss: 8.2357 Epoch 14/15 469/469 [==============================] - 9s 20ms/step - loss: 34.9921 - distortion_loss: 0.0767 - rate_loss: 11.9826 - distortion_pass_through_loss: 0.0767 - rate_pass_through_loss: 11.9821 - val_loss: 31.6609 - val_distortion_loss: 0.0783 - val_rate_loss: 8.1636 - val_distortion_pass_through_loss: 0.0784 - val_rate_pass_through_loss: 8.1657 Epoch 15/15 469/469 [==============================] - 9s 20ms/step - loss: 34.3623 - distortion_loss: 0.0760 - rate_loss: 11.5580 - distortion_pass_through_loss: 0.0760 - rate_pass_through_loss: 11.5578 - val_loss: 31.5164 - val_distortion_loss: 0.0762 - val_rate_loss: 8.6582 - val_distortion_pass_through_loss: 0.0762 - val_rate_pass_through_loss: 8.6660

The strings begin to get much shorter now, on the order of one byte per digit. However, this comes at a cost. More digits are becoming unrecognizable.
This demonstrates that this model is agnostic to human perceptions of error, it just measures the absolute deviation in terms of pixel values. To achieve a better perceived image quality, we would need to replace the pixel loss with a perceptual loss.
Use the decoder as a generative model.
If we feed the decoder random bits, this will effectively sample from the distribution that the model learned to represent digits.
First, re-instantiate the compressor/decompressor without a sanity check that would detect if the input string isn't completely decoded.
compressor, decompressor = make_mnist_codec(trainer, decode_sanity_check=False)
Now, feed long enough random strings into the decompressor so that it can decode/sample digits from them.
import os
strings = tf.constant([os.urandom(8) for _ in range(16)])
samples = decompressor(strings)
fig, axes = plt.subplots(4, 4, sharex=True, sharey=True, figsize=(5, 5))
axes = axes.ravel()
for i in range(len(axes)):
axes[i].imshow(tf.squeeze(samples[i]))
axes[i].axis("off")
plt.subplots_adjust(wspace=0, hspace=0, left=0, right=1, bottom=0, top=1)

