 View on TensorFlow.org
|
 Run in Google Colab
|
 View on GitHub
|
 Download notebook
|
In AI applications that are safety-critical, such as medical decision making and autonomous driving, or where the data is inherently noisy (for example, natural language understanding), it is important for a deep classifier to reliably quantify its uncertainty. The deep classifier should be able to be aware of its own limitations and when it should hand control over to the human experts. This tutorial shows how to improve a deep classifier's ability in quantifying uncertainty using a technique called Spectral-normalized Neural Gaussian Process (SNGP{.external}).
The core idea of SNGP is to improve a deep classifier's distance awareness by applying simple modifications to the network. A model's distance awareness is a measure of how its predictive probability reflects the distance between the test example and the training data. This is a desirable property that is common for gold-standard probabilistic models (for example, the Gaussian process{.external} with RBF kernels) but is lacking in models with deep neural networks. SNGP provides a simple way to inject this Gaussian-process behavior into a deep classifier while maintaining its predictive accuracy.
This tutorial implements a deep residual network (ResNet)-based SNGP model on scikit-learn’s two moons{.external} dataset, and compares its uncertainty surface with that of two other popular uncertainty approaches: Monte Carlo dropout{.external} and Deep ensemble{.external}.
This tutorial illustrates the SNGP model on a toy 2D dataset. For an example of applying SNGP to a real-world natural language understanding task using a BERT-base, check out the SNGP-BERT tutorial. For high-quality implementations of an SNGP model (and many other uncertainty methods) on a wide variety of benchmark datasets (such as CIFAR-100, ImageNet, Jigsaw toxicity detection, etc), refer to the Uncertainty Baselines{.external} benchmark.
About SNGP
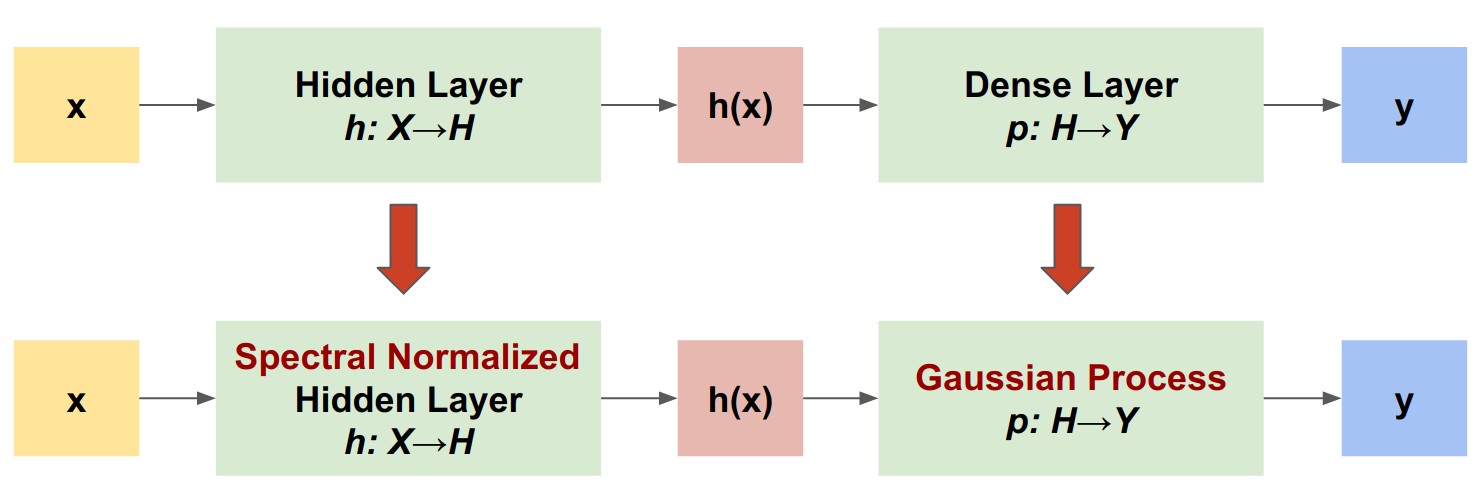
SNGP is a simple approach to improve a deep classifier's uncertainty quality while maintaining a similar level of accuracy and latency. Given a deep residual network, SNGP makes two simple changes to the model:
- It applies spectral normalization to the hidden residual layers.
- It replaces the Dense output layer with a Gaussian process layer.
Compared to other uncertainty approaches (such as Monte Carlo dropout or Deep ensemble), SNGP has several advantages:
- It works for a wide range of state-of-the-art residual-based architectures (for example, (Wide) ResNet, DenseNet, or BERT).
- It is a single-model method—it does not rely on ensemble averaging). Therefore, SNGP has a similar level of latency as a single deterministic network, and can be scaled easily to large datasets like ImageNet{.external} and Jigsaw Toxic Comments classification{.external}.
- It has strong out-of-domain detection performance due to the distance-awareness property.
The downsides of this method are:
The predictive uncertainty of SNGP is computed using the Laplace approximation{.external}. Therefore, theoretically, the posterior uncertainty of SNGP is different from that of an exact Gaussian process.
SNGP training needs a covariance reset step at the beginning of a new epoch. This can add a tiny amount of extra complexity to a training pipeline. This tutorial shows a simple way to implement this using Keras callbacks.
Setup
pip install -U -q --use-deprecated=legacy-resolver tf-models-official tensorflow
# refresh pkg_resources so it takes the changes into account.
import pkg_resources
import importlib
importlib.reload(pkg_resources)
<module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.9/site-packages/pkg_resources/__init__.py'>
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import sklearn.datasets
import numpy as np
import tensorflow as tf
import official.nlp.modeling.layers as nlp_layers
2022-12-22 02:21:18.545232: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer.so.7'; dlerror: libnvinfer.so.7: cannot open shared object file: No such file or directory 2022-12-22 02:21:18.545333: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer_plugin.so.7'; dlerror: libnvinfer_plugin.so.7: cannot open shared object file: No such file or directory 2022-12-22 02:21:18.545343: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Cannot dlopen some TensorRT libraries. If you would like to use Nvidia GPU with TensorRT, please make sure the missing libraries mentioned above are installed properly.
Define visualization macros
plt.rcParams['figure.dpi'] = 140
DEFAULT_X_RANGE = (-3.5, 3.5)
DEFAULT_Y_RANGE = (-2.5, 2.5)
DEFAULT_CMAP = colors.ListedColormap(["#377eb8", "#ff7f00"])
DEFAULT_NORM = colors.Normalize(vmin=0, vmax=1,)
DEFAULT_N_GRID = 100
The two moon dataset
Create the training and evaluation datasets from the scikit-learn two moon dataset{.external}.
def make_training_data(sample_size=500):
"""Create two moon training dataset."""
train_examples, train_labels = sklearn.datasets.make_moons(
n_samples=2 * sample_size, noise=0.1)
# Adjust data position slightly.
train_examples[train_labels == 0] += [-0.1, 0.2]
train_examples[train_labels == 1] += [0.1, -0.2]
return train_examples, train_labels
Evaluate the model's predictive behavior over the entire 2D input space.
def make_testing_data(x_range=DEFAULT_X_RANGE, y_range=DEFAULT_Y_RANGE, n_grid=DEFAULT_N_GRID):
"""Create a mesh grid in 2D space."""
# testing data (mesh grid over data space)
x = np.linspace(x_range[0], x_range[1], n_grid)
y = np.linspace(y_range[0], y_range[1], n_grid)
xv, yv = np.meshgrid(x, y)
return np.stack([xv.flatten(), yv.flatten()], axis=-1)
To evaluate model uncertainty, add an out-of-domain (OOD) dataset that belongs to a third class. The model never observes these OOD examples during training.
def make_ood_data(sample_size=500, means=(2.5, -1.75), vars=(0.01, 0.01)):
return np.random.multivariate_normal(
means, cov=np.diag(vars), size=sample_size)
# Load the train, test and OOD datasets.
train_examples, train_labels = make_training_data(
sample_size=500)
test_examples = make_testing_data()
ood_examples = make_ood_data(sample_size=500)
# Visualize
pos_examples = train_examples[train_labels == 0]
neg_examples = train_examples[train_labels == 1]
plt.figure(figsize=(7, 5.5))
plt.scatter(pos_examples[:, 0], pos_examples[:, 1], c="#377eb8", alpha=0.5)
plt.scatter(neg_examples[:, 0], neg_examples[:, 1], c="#ff7f00", alpha=0.5)
plt.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
plt.legend(["Positive", "Negative", "Out-of-Domain"])
plt.ylim(DEFAULT_Y_RANGE)
plt.xlim(DEFAULT_X_RANGE)
plt.show()
Here, the blue and orange represent the positive and negative classes, and the red represents the OOD data. A model that quantifies the uncertainty well is expected to be confident when close to training data (i.e., \(p(x_{test})\) close to 0 or 1), and be uncertain when far away from the training data regions (i.e., \(p(x_{test})\) close to 0.5).
The deterministic model
Define model
Start from the (baseline) deterministic model: a multi-layer residual network (ResNet) with dropout regularization.
class DeepResNet(tf.keras.Model):
"""Defines a multi-layer residual network."""
def __init__(self, num_classes, num_layers=3, num_hidden=128,
dropout_rate=0.1, **classifier_kwargs):
super().__init__()
# Defines class meta data.
self.num_hidden = num_hidden
self.num_layers = num_layers
self.dropout_rate = dropout_rate
self.classifier_kwargs = classifier_kwargs
# Defines the hidden layers.
self.input_layer = tf.keras.layers.Dense(self.num_hidden, trainable=False)
self.dense_layers = [self.make_dense_layer() for _ in range(num_layers)]
# Defines the output layer.
self.classifier = self.make_output_layer(num_classes)
def call(self, inputs):
# Projects the 2d input data to high dimension.
hidden = self.input_layer(inputs)
# Computes the ResNet hidden representations.
for i in range(self.num_layers):
resid = self.dense_layers[i](hidden)
resid = tf.keras.layers.Dropout(self.dropout_rate)(resid)
hidden += resid
return self.classifier(hidden)
def make_dense_layer(self):
"""Uses the Dense layer as the hidden layer."""
return tf.keras.layers.Dense(self.num_hidden, activation="relu")
def make_output_layer(self, num_classes):
"""Uses the Dense layer as the output layer."""
return tf.keras.layers.Dense(
num_classes, **self.classifier_kwargs)
This tutorial uses a six-layer ResNet with 128 hidden units.
resnet_config = dict(num_classes=2, num_layers=6, num_hidden=128)
resnet_model = DeepResNet(**resnet_config)
resnet_model.build((None, 2))
resnet_model.summary()
Model: "deep_res_net"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) multiple 384
dense_1 (Dense) multiple 16512
dense_2 (Dense) multiple 16512
dense_3 (Dense) multiple 16512
dense_4 (Dense) multiple 16512
dense_5 (Dense) multiple 16512
dense_6 (Dense) multiple 16512
dense_7 (Dense) multiple 258
=================================================================
Total params: 99,714
Trainable params: 99,330
Non-trainable params: 384
_________________________________________________________________
Train model
Configure the training parameters to use SparseCategoricalCrossentropy as the loss function and the Adam optimizer.
loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
metrics = tf.keras.metrics.SparseCategoricalAccuracy(),
optimizer = tf.keras.optimizers.legacy.Adam(learning_rate=1e-4)
train_config = dict(loss=loss, metrics=metrics, optimizer=optimizer)
Train the model for 100 epochs with batch size 128.
fit_config = dict(batch_size=128, epochs=100)
resnet_model.compile(**train_config)
resnet_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 3s 4ms/step - loss: 0.8822 - sparse_categorical_accuracy: 0.5250 Epoch 2/100 8/8 [==============================] - 0s 3ms/step - loss: 0.4462 - sparse_categorical_accuracy: 0.8100 Epoch 3/100 8/8 [==============================] - 0s 3ms/step - loss: 0.3058 - sparse_categorical_accuracy: 0.8810 Epoch 4/100 8/8 [==============================] - 0s 3ms/step - loss: 0.2326 - sparse_categorical_accuracy: 0.9030 Epoch 5/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1852 - sparse_categorical_accuracy: 0.9220 Epoch 6/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1609 - sparse_categorical_accuracy: 0.9370 Epoch 7/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1424 - sparse_categorical_accuracy: 0.9450 Epoch 8/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1375 - sparse_categorical_accuracy: 0.9410 Epoch 9/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1313 - sparse_categorical_accuracy: 0.9400 Epoch 10/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1287 - sparse_categorical_accuracy: 0.9380 Epoch 11/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1165 - sparse_categorical_accuracy: 0.9430 Epoch 12/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1134 - sparse_categorical_accuracy: 0.9450 Epoch 13/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1104 - sparse_categorical_accuracy: 0.9470 Epoch 14/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1040 - sparse_categorical_accuracy: 0.9440 Epoch 15/100 8/8 [==============================] - 0s 3ms/step - loss: 0.1014 - sparse_categorical_accuracy: 0.9470 Epoch 16/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0988 - sparse_categorical_accuracy: 0.9520 Epoch 17/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0944 - sparse_categorical_accuracy: 0.9500 Epoch 18/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0958 - sparse_categorical_accuracy: 0.9520 Epoch 19/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0920 - sparse_categorical_accuracy: 0.9510 Epoch 20/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0888 - sparse_categorical_accuracy: 0.9520 Epoch 21/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0859 - sparse_categorical_accuracy: 0.9590 Epoch 22/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0861 - sparse_categorical_accuracy: 0.9500 Epoch 23/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0822 - sparse_categorical_accuracy: 0.9580 Epoch 24/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0799 - sparse_categorical_accuracy: 0.9580 Epoch 25/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0769 - sparse_categorical_accuracy: 0.9600 Epoch 26/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0816 - sparse_categorical_accuracy: 0.9580 Epoch 27/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0747 - sparse_categorical_accuracy: 0.9630 Epoch 28/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0713 - sparse_categorical_accuracy: 0.9610 Epoch 29/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0803 - sparse_categorical_accuracy: 0.9580 Epoch 30/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0757 - sparse_categorical_accuracy: 0.9590 Epoch 31/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0734 - sparse_categorical_accuracy: 0.9580 Epoch 32/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0734 - sparse_categorical_accuracy: 0.9620 Epoch 33/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0730 - sparse_categorical_accuracy: 0.9640 Epoch 34/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0698 - sparse_categorical_accuracy: 0.9630 Epoch 35/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0672 - sparse_categorical_accuracy: 0.9700 Epoch 36/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0652 - sparse_categorical_accuracy: 0.9710 Epoch 37/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0616 - sparse_categorical_accuracy: 0.9750 Epoch 38/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0641 - sparse_categorical_accuracy: 0.9740 Epoch 39/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0623 - sparse_categorical_accuracy: 0.9700 Epoch 40/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0648 - sparse_categorical_accuracy: 0.9720 Epoch 41/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0563 - sparse_categorical_accuracy: 0.9780 Epoch 42/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0587 - sparse_categorical_accuracy: 0.9740 Epoch 43/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0575 - sparse_categorical_accuracy: 0.9780 Epoch 44/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0564 - sparse_categorical_accuracy: 0.9740 Epoch 45/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0599 - sparse_categorical_accuracy: 0.9720 Epoch 46/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0569 - sparse_categorical_accuracy: 0.9780 Epoch 47/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0519 - sparse_categorical_accuracy: 0.9810 Epoch 48/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0530 - sparse_categorical_accuracy: 0.9780 Epoch 49/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0512 - sparse_categorical_accuracy: 0.9800 Epoch 50/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0503 - sparse_categorical_accuracy: 0.9830 Epoch 51/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0465 - sparse_categorical_accuracy: 0.9810 Epoch 52/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0494 - sparse_categorical_accuracy: 0.9830 Epoch 53/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0419 - sparse_categorical_accuracy: 0.9890 Epoch 54/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0436 - sparse_categorical_accuracy: 0.9850 Epoch 55/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0463 - sparse_categorical_accuracy: 0.9820 Epoch 56/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0408 - sparse_categorical_accuracy: 0.9870 Epoch 57/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0399 - sparse_categorical_accuracy: 0.9870 Epoch 58/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0388 - sparse_categorical_accuracy: 0.9880 Epoch 59/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0532 - sparse_categorical_accuracy: 0.9830 Epoch 60/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0383 - sparse_categorical_accuracy: 0.9890 Epoch 61/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0388 - sparse_categorical_accuracy: 0.9890 Epoch 62/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0443 - sparse_categorical_accuracy: 0.9850 Epoch 63/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0349 - sparse_categorical_accuracy: 0.9880 Epoch 64/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0332 - sparse_categorical_accuracy: 0.9910 Epoch 65/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0363 - sparse_categorical_accuracy: 0.9880 Epoch 66/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0332 - sparse_categorical_accuracy: 0.9900 Epoch 67/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0388 - sparse_categorical_accuracy: 0.9850 Epoch 68/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0333 - sparse_categorical_accuracy: 0.9920 Epoch 69/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0323 - sparse_categorical_accuracy: 0.9910 Epoch 70/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0390 - sparse_categorical_accuracy: 0.9920 Epoch 71/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0313 - sparse_categorical_accuracy: 0.9920 Epoch 72/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0332 - sparse_categorical_accuracy: 0.9890 Epoch 73/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0259 - sparse_categorical_accuracy: 0.9930 Epoch 74/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0289 - sparse_categorical_accuracy: 0.9890 Epoch 75/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0269 - sparse_categorical_accuracy: 0.9910 Epoch 76/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0271 - sparse_categorical_accuracy: 0.9930 Epoch 77/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0329 - sparse_categorical_accuracy: 0.9900 Epoch 78/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0276 - sparse_categorical_accuracy: 0.9920 Epoch 79/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0263 - sparse_categorical_accuracy: 0.9930 Epoch 80/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0235 - sparse_categorical_accuracy: 0.9920 Epoch 81/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0245 - sparse_categorical_accuracy: 0.9910 Epoch 82/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0271 - sparse_categorical_accuracy: 0.9910 Epoch 83/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0269 - sparse_categorical_accuracy: 0.9950 Epoch 84/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0296 - sparse_categorical_accuracy: 0.9910 Epoch 85/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0226 - sparse_categorical_accuracy: 0.9910 Epoch 86/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0209 - sparse_categorical_accuracy: 0.9940 Epoch 87/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0228 - sparse_categorical_accuracy: 0.9940 Epoch 88/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0214 - sparse_categorical_accuracy: 0.9940 Epoch 89/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0216 - sparse_categorical_accuracy: 0.9930 Epoch 90/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0230 - sparse_categorical_accuracy: 0.9920 Epoch 91/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0177 - sparse_categorical_accuracy: 0.9950 Epoch 92/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0197 - sparse_categorical_accuracy: 0.9940 Epoch 93/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0220 - sparse_categorical_accuracy: 0.9920 Epoch 94/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0170 - sparse_categorical_accuracy: 0.9960 Epoch 95/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0219 - sparse_categorical_accuracy: 0.9910 Epoch 96/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0231 - sparse_categorical_accuracy: 0.9930 Epoch 97/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0212 - sparse_categorical_accuracy: 0.9940 Epoch 98/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0157 - sparse_categorical_accuracy: 0.9970 Epoch 99/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0206 - sparse_categorical_accuracy: 0.9930 Epoch 100/100 8/8 [==============================] - 0s 3ms/step - loss: 0.0179 - sparse_categorical_accuracy: 0.9950 <keras.callbacks.History at 0x7fab7009ac40>
Visualize uncertainty
def plot_uncertainty_surface(test_uncertainty, ax, cmap=None):
"""Visualizes the 2D uncertainty surface.
For simplicity, assume these objects already exist in the memory:
test_examples: Array of test examples, shape (num_test, 2).
train_labels: Array of train labels, shape (num_train, ).
train_examples: Array of train examples, shape (num_train, 2).
Arguments:
test_uncertainty: Array of uncertainty scores, shape (num_test,).
ax: A matplotlib Axes object that specifies a matplotlib figure.
cmap: A matplotlib colormap object specifying the palette of the
predictive surface.
Returns:
pcm: A matplotlib PathCollection object that contains the palette
information of the uncertainty plot.
"""
# Normalize uncertainty for better visualization.
test_uncertainty = test_uncertainty / np.max(test_uncertainty)
# Set view limits.
ax.set_ylim(DEFAULT_Y_RANGE)
ax.set_xlim(DEFAULT_X_RANGE)
# Plot normalized uncertainty surface.
pcm = ax.imshow(
np.reshape(test_uncertainty, [DEFAULT_N_GRID, DEFAULT_N_GRID]),
cmap=cmap,
origin="lower",
extent=DEFAULT_X_RANGE + DEFAULT_Y_RANGE,
vmin=DEFAULT_NORM.vmin,
vmax=DEFAULT_NORM.vmax,
interpolation='bicubic',
aspect='auto')
# Plot training data.
ax.scatter(train_examples[:, 0], train_examples[:, 1],
c=train_labels, cmap=DEFAULT_CMAP, alpha=0.5)
ax.scatter(ood_examples[:, 0], ood_examples[:, 1], c="red", alpha=0.1)
return pcm
Now visualize the predictions of the deterministic model. First plot the class probability:
\[p(x) = softmax(logit(x))\]
resnet_logits = resnet_model(test_examples)
resnet_probs = tf.nn.softmax(resnet_logits, axis=-1)[:, 0] # Take the probability for class 0.
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_probs, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Class Probability, Deterministic Model")
plt.show()
In this plot, the yellow and purple are the predictive probabilities for the two classes. The deterministic model did a good job in classifying the two known classes—blue and orange—with a nonlinear decision boundary. However, it is not distance-aware, and classified the never-observed red out-of-domain (OOD) examples confidently as the orange class.
Visualize the model uncertainty by computing the predictive variance:
\[var(x) = p(x) * (1 - p(x))\]
resnet_uncertainty = resnet_probs * (1 - resnet_probs)
_, ax = plt.subplots(figsize=(7, 5.5))
pcm = plot_uncertainty_surface(resnet_uncertainty, ax=ax)
plt.colorbar(pcm, ax=ax)
plt.title("Predictive Uncertainty, Deterministic Model")
plt.show()
In this plot, the yellow indicates high uncertainty, and the purple indicates low uncertainty. A deterministic ResNet's uncertainty depends only on the test examples' distance from the decision boundary. This leads the model to be over-confident when out of the training domain. The next section shows how SNGP behaves differently on this dataset.
The SNGP model
Define SNGP model
Let's now implement the SNGP model. Both the SNGP components, SpectralNormalization and RandomFeatureGaussianProcess, are available at the tensorflow_model's built-in layers.
Let's inspect these two components in more detail. (You can also jump to the full SNGP model section to learn how SNGP is implemented.)
SpectralNormalization wrapper
SpectralNormalization{.external} is a Keras layer wrapper. It can be applied to an existing Dense layer like this:
dense = tf.keras.layers.Dense(units=10)
dense = nlp_layers.SpectralNormalization(dense, norm_multiplier=0.9)
Spectral normalization regularizes the hidden weight \(W\) by gradually guiding its spectral norm (that is, the largest eigenvalue of \(W\)) toward the target value norm_multiplier).
The Gaussian Process (GP) layer
RandomFeatureGaussianProcess{.external} implements a random-feature based approximation{.external} to a Gaussian process model that is end-to-end trainable with a deep neural network. Under the hood, the Gaussian process layer implements a two-layer network:
\[logits(x) = \Phi(x) \beta, \quad \Phi(x)=\sqrt{\frac{2}{M} } * cos(Wx + b)\]
Here, \(x\) is the input, and \(W\) and \(b\) are frozen weights initialized randomly from Gaussian and Uniform distributions, respectively. (Therefore, \(\Phi(x)\) are called "random features".) \(\beta\) is the learnable kernel weight similar to that of a Dense layer.
batch_size = 32
input_dim = 1024
num_classes = 10
gp_layer = nlp_layers.RandomFeatureGaussianProcess(units=num_classes,
num_inducing=1024,
normalize_input=False,
scale_random_features=True,
gp_cov_momentum=-1)
The main parameters of the GP layers are:
units: The dimension of the output logits.num_inducing: The dimension \(M\) of the hidden weight \(W\). Default to 1024.normalize_input: Whether to apply layer normalization to the input \(x\).scale_random_features: Whether to apply the scale \(\sqrt{2/M}\) to the hidden output.
gp_cov_momentumcontrols how the model covariance is computed. If set to a positive value (for example,0.999), the covariance matrix is computed using the momentum-based moving average update (similar to batch normalization). If set to-1, the covariance matrix is updated without momentum.
Given a batch input with shape (batch_size, input_dim), the GP layer returns a logits tensor (shape (batch_size, num_classes)) for prediction, and also covmat tensor (shape (batch_size, batch_size)) which is the posterior covariance matrix of the batch logits.
embedding = tf.random.normal(shape=(batch_size, input_dim))
logits, covmat = gp_layer(embedding)
Theoretically, it is possible to extend the algorithm to compute different variance values for different classes (as introduced in the original SNGP paper{.external}). However, this is difficult to scale to problems with large output spaces (such as classification with ImageNet or language modeling).
The full SNGP model
Given the base class DeepResNet, the SNGP model can be implemented easily by modifying the residual network's hidden and output layers. For compatibility with Keras model.fit() API, also modify the model's call() method so it only outputs logits during training.
class DeepResNetSNGP(DeepResNet):
def __init__(self, spec_norm_bound=0.9, **kwargs):
self.spec_norm_bound = spec_norm_bound
super().__init__(**kwargs)
def make_dense_layer(self):
"""Applies spectral normalization to the hidden layer."""
dense_layer = super().make_dense_layer()
return nlp_layers.SpectralNormalization(
dense_layer, norm_multiplier=self.spec_norm_bound)
def make_output_layer(self, num_classes):
"""Uses Gaussian process as the output layer."""
return nlp_layers.RandomFeatureGaussianProcess(
num_classes,
gp_cov_momentum=-1,
**self.classifier_kwargs)
def call(self, inputs, training=False, return_covmat=False):
# Gets logits and a covariance matrix from the GP layer.
logits, covmat = super().call(inputs)
# Returns only logits during training.
if not training and return_covmat:
return logits, covmat
return logits
Use the same architecture as the deterministic model.
resnet_config
{'num_classes': 2, 'num_layers': 6, 'num_hidden': 128}
sngp_model = DeepResNetSNGP(**resnet_config)
sngp_model.build((None, 2))
sngp_model.summary()
WARNING:tensorflow:From /tmpfs/src/tf_docs_env/lib/python3.9/site-packages/tensorflow/python/autograph/pyct/static_analysis/liveness.py:83: Analyzer.lamba_check (from tensorflow.python.autograph.pyct.static_analysis.liveness) is deprecated and will be removed after 2023-09-23.
Instructions for updating:
Lambda fuctions will be no more assumed to be used in the statement where they are used, or at least in the same block. https://github.com/tensorflow/tensorflow/issues/56089
Model: "deep_res_net_sngp"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_9 (Dense) multiple 384
spectral_normalization_1 (S multiple 16768
pectralNormalization)
spectral_normalization_2 (S multiple 16768
pectralNormalization)
spectral_normalization_3 (S multiple 16768
pectralNormalization)
spectral_normalization_4 (S multiple 16768
pectralNormalization)
spectral_normalization_5 (S multiple 16768
pectralNormalization)
spectral_normalization_6 (S multiple 16768
pectralNormalization)
random_feature_gaussian_pro multiple 1182722
cess (RandomFeatureGaussian
Process)
=================================================================
Total params: 1,283,714
Trainable params: 101,120
Non-trainable params: 1,182,594
_________________________________________________________________
Implement a Keras callback to reset the covariance matrix at the beginning of a new epoch.
class ResetCovarianceCallback(tf.keras.callbacks.Callback):
def on_epoch_begin(self, epoch, logs=None):
"""Resets covariance matrix at the beginning of the epoch."""
if epoch > 0:
self.model.classifier.reset_covariance_matrix()
Add this callback to the DeepResNetSNGP model class.
class DeepResNetSNGPWithCovReset(DeepResNetSNGP):
def fit(self, *args, **kwargs):
"""Adds ResetCovarianceCallback to model callbacks."""
kwargs["callbacks"] = list(kwargs.get("callbacks", []))
kwargs["callbacks"].append(ResetCovarianceCallback())
return super().fit(*args, **kwargs)
Train model
Use tf.keras.model.fit to train the model.
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, **fit_config)
Epoch 1/100 8/8 [==============================] - 2s 4ms/step - loss: 0.6481 - sparse_categorical_accuracy: 0.8915 Epoch 2/100 8/8 [==============================] - 0s 4ms/step - loss: 0.5621 - sparse_categorical_accuracy: 0.9960 Epoch 3/100 8/8 [==============================] - 0s 4ms/step - loss: 0.5094 - sparse_categorical_accuracy: 1.0000 Epoch 4/100 8/8 [==============================] - 0s 4ms/step - loss: 0.4721 - sparse_categorical_accuracy: 1.0000 Epoch 5/100 8/8 [==============================] - 0s 4ms/step - loss: 0.4373 - sparse_categorical_accuracy: 1.0000 Epoch 6/100 8/8 [==============================] - 0s 4ms/step - loss: 0.4098 - sparse_categorical_accuracy: 1.0000 Epoch 7/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3851 - sparse_categorical_accuracy: 0.9990 Epoch 8/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3639 - sparse_categorical_accuracy: 0.9990 Epoch 9/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3468 - sparse_categorical_accuracy: 0.9990 Epoch 10/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3281 - sparse_categorical_accuracy: 0.9990 Epoch 11/100 8/8 [==============================] - 0s 4ms/step - loss: 0.3122 - sparse_categorical_accuracy: 0.9990 Epoch 12/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2979 - sparse_categorical_accuracy: 0.9990 Epoch 13/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2844 - sparse_categorical_accuracy: 0.9990 Epoch 14/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2710 - sparse_categorical_accuracy: 0.9990 Epoch 15/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2608 - sparse_categorical_accuracy: 0.9970 Epoch 16/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2491 - sparse_categorical_accuracy: 0.9990 Epoch 17/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2400 - sparse_categorical_accuracy: 0.9990 Epoch 18/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2315 - sparse_categorical_accuracy: 0.9990 Epoch 19/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2236 - sparse_categorical_accuracy: 0.9980 Epoch 20/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2147 - sparse_categorical_accuracy: 0.9990 Epoch 21/100 8/8 [==============================] - 0s 4ms/step - loss: 0.2062 - sparse_categorical_accuracy: 0.9980 Epoch 22/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1997 - sparse_categorical_accuracy: 0.9980 Epoch 23/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1931 - sparse_categorical_accuracy: 0.9990 Epoch 24/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1887 - sparse_categorical_accuracy: 0.9980 Epoch 25/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1797 - sparse_categorical_accuracy: 0.9990 Epoch 26/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1754 - sparse_categorical_accuracy: 0.9980 Epoch 27/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1710 - sparse_categorical_accuracy: 0.9980 Epoch 28/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1652 - sparse_categorical_accuracy: 0.9980 Epoch 29/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1605 - sparse_categorical_accuracy: 0.9980 Epoch 30/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1565 - sparse_categorical_accuracy: 0.9980 Epoch 31/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1514 - sparse_categorical_accuracy: 0.9990 Epoch 32/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1474 - sparse_categorical_accuracy: 0.9990 Epoch 33/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1438 - sparse_categorical_accuracy: 0.9990 Epoch 34/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1399 - sparse_categorical_accuracy: 0.9990 Epoch 35/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1348 - sparse_categorical_accuracy: 0.9990 Epoch 36/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1323 - sparse_categorical_accuracy: 0.9990 Epoch 37/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1292 - sparse_categorical_accuracy: 0.9990 Epoch 38/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1258 - sparse_categorical_accuracy: 0.9990 Epoch 39/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1228 - sparse_categorical_accuracy: 0.9990 Epoch 40/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1203 - sparse_categorical_accuracy: 0.9990 Epoch 41/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1168 - sparse_categorical_accuracy: 0.9990 Epoch 42/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1137 - sparse_categorical_accuracy: 0.9990 Epoch 43/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1118 - sparse_categorical_accuracy: 0.9990 Epoch 44/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1083 - sparse_categorical_accuracy: 0.9990 Epoch 45/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1069 - sparse_categorical_accuracy: 0.9990 Epoch 46/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1032 - sparse_categorical_accuracy: 0.9980 Epoch 47/100 8/8 [==============================] - 0s 4ms/step - loss: 0.1029 - sparse_categorical_accuracy: 0.9990 Epoch 48/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0986 - sparse_categorical_accuracy: 0.9990 Epoch 49/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0968 - sparse_categorical_accuracy: 0.9990 Epoch 50/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0947 - sparse_categorical_accuracy: 0.9990 Epoch 51/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0933 - sparse_categorical_accuracy: 0.9990 Epoch 52/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0907 - sparse_categorical_accuracy: 0.9990 Epoch 53/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0890 - sparse_categorical_accuracy: 0.9990 Epoch 54/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0874 - sparse_categorical_accuracy: 0.9990 Epoch 55/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0854 - sparse_categorical_accuracy: 0.9990 Epoch 56/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0839 - sparse_categorical_accuracy: 0.9990 Epoch 57/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0828 - sparse_categorical_accuracy: 0.9990 Epoch 58/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0807 - sparse_categorical_accuracy: 0.9990 Epoch 59/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0792 - sparse_categorical_accuracy: 0.9990 Epoch 60/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0773 - sparse_categorical_accuracy: 0.9990 Epoch 61/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0761 - sparse_categorical_accuracy: 0.9990 Epoch 62/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0746 - sparse_categorical_accuracy: 0.9990 Epoch 63/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0735 - sparse_categorical_accuracy: 0.9990 Epoch 64/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0721 - sparse_categorical_accuracy: 0.9990 Epoch 65/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0703 - sparse_categorical_accuracy: 0.9990 Epoch 66/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0685 - sparse_categorical_accuracy: 0.9990 Epoch 67/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0679 - sparse_categorical_accuracy: 0.9990 Epoch 68/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0666 - sparse_categorical_accuracy: 1.0000 Epoch 69/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0654 - sparse_categorical_accuracy: 0.9990 Epoch 70/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0653 - sparse_categorical_accuracy: 0.9990 Epoch 71/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0636 - sparse_categorical_accuracy: 0.9990 Epoch 72/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0621 - sparse_categorical_accuracy: 1.0000 Epoch 73/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0612 - sparse_categorical_accuracy: 1.0000 Epoch 74/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0603 - sparse_categorical_accuracy: 1.0000 Epoch 75/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0596 - sparse_categorical_accuracy: 0.9990 Epoch 76/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0584 - sparse_categorical_accuracy: 0.9990 Epoch 77/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0570 - sparse_categorical_accuracy: 0.9990 Epoch 78/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0566 - sparse_categorical_accuracy: 1.0000 Epoch 79/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0547 - sparse_categorical_accuracy: 1.0000 Epoch 80/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0547 - sparse_categorical_accuracy: 1.0000 Epoch 81/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0533 - sparse_categorical_accuracy: 1.0000 Epoch 82/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0528 - sparse_categorical_accuracy: 1.0000 Epoch 83/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0521 - sparse_categorical_accuracy: 1.0000 Epoch 84/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0512 - sparse_categorical_accuracy: 1.0000 Epoch 85/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0509 - sparse_categorical_accuracy: 1.0000 Epoch 86/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0495 - sparse_categorical_accuracy: 1.0000 Epoch 87/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0493 - sparse_categorical_accuracy: 1.0000 Epoch 88/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0483 - sparse_categorical_accuracy: 1.0000 Epoch 89/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0473 - sparse_categorical_accuracy: 1.0000 Epoch 90/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0467 - sparse_categorical_accuracy: 1.0000 Epoch 91/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0462 - sparse_categorical_accuracy: 1.0000 Epoch 92/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0454 - sparse_categorical_accuracy: 1.0000 Epoch 93/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0448 - sparse_categorical_accuracy: 1.0000 Epoch 94/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0443 - sparse_categorical_accuracy: 1.0000 Epoch 95/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0440 - sparse_categorical_accuracy: 1.0000 Epoch 96/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0427 - sparse_categorical_accuracy: 1.0000 Epoch 97/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0425 - sparse_categorical_accuracy: 1.0000 Epoch 98/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0414 - sparse_categorical_accuracy: 1.0000 Epoch 99/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0414 - sparse_categorical_accuracy: 1.0000 Epoch 100/100 8/8 [==============================] - 0s 4ms/step - loss: 0.0407 - sparse_categorical_accuracy: 1.0000 <keras.callbacks.History at 0x7fab6029cf10>
Visualize uncertainty
First compute the predictive logits and variances.
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_variance = tf.linalg.diag_part(sngp_covmat)[:, None]
Now compute the posterior predictive probability. The classic method for computing the predictive probability of a probabilistic model is to use Monte Carlo sampling, i.e.,
\[E(p(x)) = \frac{1}{M} \sum_{m=1}^M logit_m(x), \]
where \(M\) is the sample size, and \(logit_m(x)\) are random samples from the SNGP posterior \(MultivariateNormal\)(sngp_logits,sngp_covmat). However, this approach can be slow for latency-sensitive applications such as autonomous driving or real-time bidding. Instead, you can approximate \(E(p(x))\) using the mean-field method{.external}:
\[E(p(x)) \approx softmax(\frac{logit(x)}{\sqrt{1+ \lambda * \sigma^2(x)} })\]
where \(\sigma^2(x)\) is the SNGP variance, and \(\lambda\) is often chosen as \(\pi/8\) or \(3/\pi^2\).
sngp_logits_adjusted = sngp_logits / tf.sqrt(1. + (np.pi / 8.) * sngp_variance)
sngp_probs = tf.nn.softmax(sngp_logits_adjusted, axis=-1)[:, 0]
This mean-field method is implemented as a built-in function layers.gaussian_process.mean_field_logits:
def compute_posterior_mean_probability(logits, covmat, lambda_param=np.pi / 8.):
# Computes uncertainty-adjusted logits using the built-in method.
logits_adjusted = nlp_layers.gaussian_process.mean_field_logits(
logits, covmat, mean_field_factor=lambda_param)
return tf.nn.softmax(logits_adjusted, axis=-1)[:, 0]
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
SNGP Summary
def plot_predictions(pred_probs, model_name=""):
"""Plot normalized class probabilities and predictive uncertainties."""
# Compute predictive uncertainty.
uncertainty = pred_probs * (1. - pred_probs)
# Initialize the plot axes.
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
# Plots the class probability.
pcm_0 = plot_uncertainty_surface(pred_probs, ax=axs[0])
# Plots the predictive uncertainty.
pcm_1 = plot_uncertainty_surface(uncertainty, ax=axs[1])
# Adds color bars and titles.
fig.colorbar(pcm_0, ax=axs[0])
fig.colorbar(pcm_1, ax=axs[1])
axs[0].set_title(f"Class Probability, {model_name}")
axs[1].set_title(f"(Normalized) Predictive Uncertainty, {model_name}")
plt.show()
You can now put everything together. The entire procedure—training, evaluation and uncertainty computation—can be done in just five lines:
def train_and_test_sngp(train_examples, test_examples):
sngp_model = DeepResNetSNGPWithCovReset(**resnet_config)
sngp_model.compile(**train_config)
sngp_model.fit(train_examples, train_labels, verbose=0, **fit_config)
sngp_logits, sngp_covmat = sngp_model(test_examples, return_covmat=True)
sngp_probs = compute_posterior_mean_probability(sngp_logits, sngp_covmat)
return sngp_probs
sngp_probs = train_and_test_sngp(train_examples, test_examples)
Visualize the class probability (left) and the predictive uncertainty (right) of the SNGP model.
plot_predictions(sngp_probs, model_name="SNGP")
Remember that in the class probability plot (left), the yellow and purple are class probabilities. When close to the training data domain, SNGP correctly classifies the examples with high confidence (i.e., assigning near 0 or 1 probability). When far away from the training data, SNGP gradually becomes less confident, and its predictive probability becomes close to 0.5 while the (normalized) model uncertainty rises to 1.
Compare this to the uncertainty surface of the deterministic model:
plot_predictions(resnet_probs, model_name="Deterministic")
As mentioned earlier, a deterministic model is not distance-aware. Its uncertainty is defined by the distance of the test example from the decision boundary. This leads the model to produce overconfident predictions for the out-of-domain examples (red).
Comparison with other uncertainty approaches
This section compares the uncertainty of SNGP with Monte Carlo dropout{.external} and Deep ensemble{.external}.
Both of these methods are based on Monte Carlo averaging of multiple forward passes of deterministic models. First, set the ensemble size \(M\).
num_ensemble = 10
Monte Carlo dropout
Given a trained neural network with Dropout layers, Monte Carlo dropout computes the mean predictive probability
\[E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\]
by averaging over multiple Dropout-enabled forward passes \(\{logit_m(x)\}_{m=1}^M\).
def mc_dropout_sampling(test_examples):
# Enable dropout during inference.
return resnet_model(test_examples, training=True)
# Monte Carlo dropout inference.
dropout_logit_samples = [mc_dropout_sampling(test_examples) for _ in range(num_ensemble)]
dropout_prob_samples = [tf.nn.softmax(dropout_logits, axis=-1)[:, 0] for dropout_logits in dropout_logit_samples]
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
dropout_probs = tf.reduce_mean(dropout_prob_samples, axis=0)
plot_predictions(dropout_probs, model_name="MC Dropout")
Deep ensemble
Deep ensemble is a state-of-the-art (but expensive) method for deep learning uncertainty. To train a Deep ensemble, first train \(M\) ensemble members.
# Deep ensemble training
resnet_ensemble = []
for _ in range(num_ensemble):
resnet_model = DeepResNet(**resnet_config)
resnet_model.compile(optimizer=optimizer, loss=loss, metrics=metrics)
resnet_model.fit(train_examples, train_labels, verbose=0, **fit_config)
resnet_ensemble.append(resnet_model)
Collect logits and compute the mean predictive probability \(E(p(x)) = \frac{1}{M}\sum_{m=1}^M softmax(logit_m(x))\).
# Deep ensemble inference
ensemble_logit_samples = [model(test_examples) for model in resnet_ensemble]
ensemble_prob_samples = [tf.nn.softmax(logits, axis=-1)[:, 0] for logits in ensemble_logit_samples]
ensemble_probs = tf.reduce_mean(ensemble_prob_samples, axis=0)
plot_predictions(ensemble_probs, model_name="Deep ensemble")
Both the Monte Carlo Dropout and Deep ensemble methods improve the model's uncertainty ability by making the decision boundary less certain. However, they both inherit the deterministic deep network's limitation in lacking distance awareness.
Summary
In this tutorial, you have:
- Implemented the SNGP model on a deep classifier to improve its distance awareness.
- Trained the SNGP model end-to-end using Keras
Model.fitAPI. - Visualized the uncertainty behavior of SNGP.
- Compared the uncertainty behavior between SNGP, Monte Carlo dropout and deep ensemble models.
Resources and further reading
- Check out the SNGP-BERT tutorial for an example of applying SNGP on a BERT model for uncertainty-aware natural language understanding.
- Go to the Uncertainty Baselines GitHub repo{.external} for the implementation of SNGP model (and many other uncertainty methods) on a wide variety of benchmark datasets (for example, CIFAR, ImageNet, Jigsaw toxicity detection, etc).
- For a deeper understanding of the SNGP method, check out the paper titled Simple and Principled Uncertainty Estimation with Deterministic Deep Learning via Distance Awareness{.external}.