 View on TensorFlow.org
|
 Run in Google Colab
|
 View source on GitHub
|
 Download notebook
|
This tutorial demonstrates training a 3D convolutional neural network (CNN) for video classification using the UCF101 action recognition dataset. A 3D CNN uses a three-dimensional filter to perform convolutions. The kernel is able to slide in three directions, whereas in a 2D CNN it can slide in two dimensions. The model is based on the work published in A Closer Look at Spatiotemporal Convolutions for Action Recognition by D. Tran et al. (2017). In this tutorial, you will:
- Build an input pipeline
- Build a 3D convolutional neural network model with residual connections using Keras functional API
- Train the model
- Evaluate and test the model
This video classification tutorial is the second part in a series of TensorFlow video tutorials. Here are the other three tutorials:
- Load video data: This tutorial explains much of the code used in this document.
- MoViNet for streaming action recognition: Get familiar with the MoViNet models that are available on TF Hub.
- Transfer learning for video classification with MoViNet: This tutorial explains how to use a pre-trained video classification model trained on a different dataset with the UCF-101 dataset.
Setup
Begin by installing and importing some necessary libraries, including:
remotezip to inspect the contents of a ZIP file, tqdm to use a progress bar, OpenCV to process video files, einops for performing more complex tensor operations, and tensorflow_docs for embedding data in a Jupyter notebook.
pip install remotezip tqdm opencv-python einopspip install -U tensorflow keras
import tqdm
import random
import pathlib
import itertools
import collections
import cv2
import einops
import numpy as np
import remotezip as rz
import seaborn as sns
import matplotlib.pyplot as plt
import tensorflow as tf
import keras
from keras import layers
2024-07-19 07:20:00.651858: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:485] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2024-07-19 07:20:00.672979: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:8454] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2024-07-19 07:20:00.679290: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1452] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
Load and preprocess video data
The hidden cell below defines helper functions to download a slice of data from the UCF-101 dataset, and load it into a tf.data.Dataset. You can learn more about the specific preprocessing steps in the Loading video data tutorial, which walks you through this code in more detail.
The FrameGenerator class at the end of the hidden block is the most important utility here. It creates an iterable object that can feed data into the TensorFlow data pipeline. Specifically, this class contains a Python generator that loads the video frames along with its encoded label. The generator (__call__) function yields the frame array produced by frames_from_video_file and a one-hot encoded vector of the label associated with the set of frames.
def list_files_per_class(zip_url):
"""
List the files in each class of the dataset given the zip URL.
Args:
zip_url: URL from which the files can be unzipped.
Return:
files: List of files in each of the classes.
"""
files = []
with rz.RemoteZip(URL) as zip:
for zip_info in zip.infolist():
files.append(zip_info.filename)
return files
def get_class(fname):
"""
Retrieve the name of the class given a filename.
Args:
fname: Name of the file in the UCF101 dataset.
Return:
Class that the file belongs to.
"""
return fname.split('_')[-3]
def get_files_per_class(files):
"""
Retrieve the files that belong to each class.
Args:
files: List of files in the dataset.
Return:
Dictionary of class names (key) and files (values).
"""
files_for_class = collections.defaultdict(list)
for fname in files:
class_name = get_class(fname)
files_for_class[class_name].append(fname)
return files_for_class
def download_from_zip(zip_url, to_dir, file_names):
"""
Download the contents of the zip file from the zip URL.
Args:
zip_url: Zip URL containing data.
to_dir: Directory to download data to.
file_names: Names of files to download.
"""
with rz.RemoteZip(zip_url) as zip:
for fn in tqdm.tqdm(file_names):
class_name = get_class(fn)
zip.extract(fn, str(to_dir / class_name))
unzipped_file = to_dir / class_name / fn
fn = pathlib.Path(fn).parts[-1]
output_file = to_dir / class_name / fn
unzipped_file.rename(output_file,)
def split_class_lists(files_for_class, count):
"""
Returns the list of files belonging to a subset of data as well as the remainder of
files that need to be downloaded.
Args:
files_for_class: Files belonging to a particular class of data.
count: Number of files to download.
Return:
split_files: Files belonging to the subset of data.
remainder: Dictionary of the remainder of files that need to be downloaded.
"""
split_files = []
remainder = {}
for cls in files_for_class:
split_files.extend(files_for_class[cls][:count])
remainder[cls] = files_for_class[cls][count:]
return split_files, remainder
def download_ufc_101_subset(zip_url, num_classes, splits, download_dir):
"""
Download a subset of the UFC101 dataset and split them into various parts, such as
training, validation, and test.
Args:
zip_url: Zip URL containing data.
num_classes: Number of labels.
splits: Dictionary specifying the training, validation, test, etc. (key) division of data
(value is number of files per split).
download_dir: Directory to download data to.
Return:
dir: Posix path of the resulting directories containing the splits of data.
"""
files = list_files_per_class(zip_url)
for f in files:
tokens = f.split('/')
if len(tokens) <= 2:
files.remove(f) # Remove that item from the list if it does not have a filename
files_for_class = get_files_per_class(files)
classes = list(files_for_class.keys())[:num_classes]
for cls in classes:
new_files_for_class = files_for_class[cls]
random.shuffle(new_files_for_class)
files_for_class[cls] = new_files_for_class
# Only use the number of classes you want in the dictionary
files_for_class = {x: files_for_class[x] for x in list(files_for_class)[:num_classes]}
dirs = {}
for split_name, split_count in splits.items():
print(split_name, ":")
split_dir = download_dir / split_name
split_files, files_for_class = split_class_lists(files_for_class, split_count)
download_from_zip(zip_url, split_dir, split_files)
dirs[split_name] = split_dir
return dirs
def format_frames(frame, output_size):
"""
Pad and resize an image from a video.
Args:
frame: Image that needs to resized and padded.
output_size: Pixel size of the output frame image.
Return:
Formatted frame with padding of specified output size.
"""
frame = tf.image.convert_image_dtype(frame, tf.float32)
frame = tf.image.resize_with_pad(frame, *output_size)
return frame
def frames_from_video_file(video_path, n_frames, output_size = (224,224), frame_step = 15):
"""
Creates frames from each video file present for each category.
Args:
video_path: File path to the video.
n_frames: Number of frames to be created per video file.
output_size: Pixel size of the output frame image.
Return:
An NumPy array of frames in the shape of (n_frames, height, width, channels).
"""
# Read each video frame by frame
result = []
src = cv2.VideoCapture(str(video_path))
video_length = src.get(cv2.CAP_PROP_FRAME_COUNT)
need_length = 1 + (n_frames - 1) * frame_step
if need_length > video_length:
start = 0
else:
max_start = video_length - need_length
start = random.randint(0, max_start + 1)
src.set(cv2.CAP_PROP_POS_FRAMES, start)
# ret is a boolean indicating whether read was successful, frame is the image itself
ret, frame = src.read()
result.append(format_frames(frame, output_size))
for _ in range(n_frames - 1):
for _ in range(frame_step):
ret, frame = src.read()
if ret:
frame = format_frames(frame, output_size)
result.append(frame)
else:
result.append(np.zeros_like(result[0]))
src.release()
result = np.array(result)[..., [2, 1, 0]]
return result
class FrameGenerator:
def __init__(self, path, n_frames, training = False):
""" Returns a set of frames with their associated label.
Args:
path: Video file paths.
n_frames: Number of frames.
training: Boolean to determine if training dataset is being created.
"""
self.path = path
self.n_frames = n_frames
self.training = training
self.class_names = sorted(set(p.name for p in self.path.iterdir() if p.is_dir()))
self.class_ids_for_name = dict((name, idx) for idx, name in enumerate(self.class_names))
def get_files_and_class_names(self):
video_paths = list(self.path.glob('*/*.avi'))
classes = [p.parent.name for p in video_paths]
return video_paths, classes
def __call__(self):
video_paths, classes = self.get_files_and_class_names()
pairs = list(zip(video_paths, classes))
if self.training:
random.shuffle(pairs)
for path, name in pairs:
video_frames = frames_from_video_file(path, self.n_frames)
label = self.class_ids_for_name[name] # Encode labels
yield video_frames, label
URL = 'https://storage.googleapis.com/thumos14_files/UCF101_videos.zip'
download_dir = pathlib.Path('./UCF101_subset/')
subset_paths = download_ufc_101_subset(URL,
num_classes = 10,
splits = {"train": 30, "val": 10, "test": 10},
download_dir = download_dir)
train : 100%|██████████| 300/300 [00:26<00:00, 11.42it/s] val : 100%|██████████| 100/100 [00:09<00:00, 10.95it/s] test : 100%|██████████| 100/100 [00:08<00:00, 12.21it/s]
Create the training, validation, and test sets (train_ds, val_ds, and test_ds).
n_frames = 10
batch_size = 8
output_signature = (tf.TensorSpec(shape = (None, None, None, 3), dtype = tf.float32),
tf.TensorSpec(shape = (), dtype = tf.int16))
train_ds = tf.data.Dataset.from_generator(FrameGenerator(subset_paths['train'], n_frames, training=True),
output_signature = output_signature)
# Batch the data
train_ds = train_ds.batch(batch_size)
val_ds = tf.data.Dataset.from_generator(FrameGenerator(subset_paths['val'], n_frames),
output_signature = output_signature)
val_ds = val_ds.batch(batch_size)
test_ds = tf.data.Dataset.from_generator(FrameGenerator(subset_paths['test'], n_frames),
output_signature = output_signature)
test_ds = test_ds.batch(batch_size)
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR I0000 00:00:1721373647.625577 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.629001 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.632541 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.636333 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.647652 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.650707 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.653998 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.657373 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.660849 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.663827 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.667128 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373647.670523 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.920621 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.922933 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.924998 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.927126 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.929346 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.931453 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.933390 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.935399 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.937490 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.939581 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.941501 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.943519 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.982068 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.984244 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.986235 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.988770 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.990919 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.993067 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.995014 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.997056 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373648.999179 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373649.001806 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373649.004162 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355 I0000 00:00:1721373649.006617 255767 cuda_executor.cc:1015] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero. See more at https://github.com/torvalds/linux/blob/v6.0/Documentation/ABI/testing/sysfs-bus-pci#L344-L355
Create the model
The following 3D convolutional neural network model is based off the paper A Closer Look at Spatiotemporal Convolutions for Action Recognition by D. Tran et al. (2017). The paper compares several versions of 3D ResNets. Instead of operating on a single image with dimensions (height, width), like standard ResNets, these operate on video volume (time, height, width). The most obvious approach to this problem would be replace each 2D convolution (layers.Conv2D) with a 3D convolution (layers.Conv3D).
This tutorial uses a (2 + 1)D convolution with residual connections. The (2 + 1)D convolution allows for the decomposition of the spatial and temporal dimensions, therefore creating two separate steps. An advantage of this approach is that factorizing the convolutions into spatial and temporal dimensions saves parameters.
For each output location a 3D convolution combines all the vectors from a 3D patch of the volume to create one vector in the output volume.
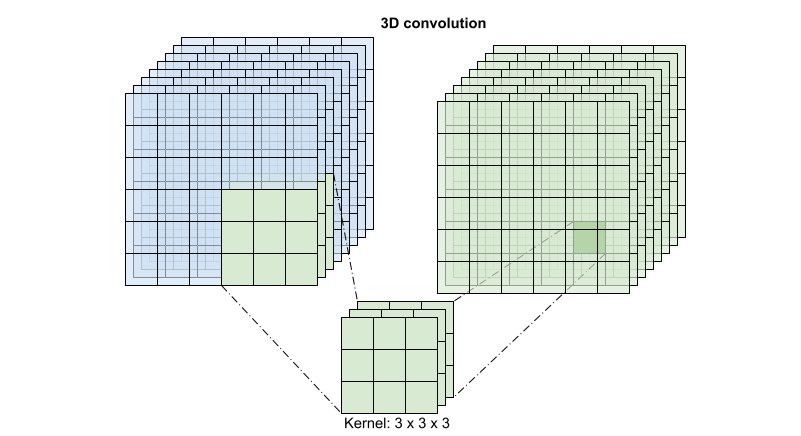
This operation is takes time * height * width * channels inputs and produces channels outputs (assuming the number of input and output channels are the same. So a 3D convolution layer with a kernel size of (3 x 3 x 3) would need a weight-matrix with 27 * channels ** 2 entries. The reference paper found that a more effective & efficient approach was to factorize the convolution. Instead of a single 3D convolution to process the time and space dimensions, they proposed a "(2+1)D" convolution which processes the space and time dimensions separately. The figure below shows the factored spatial and temporal convolutions of a (2 + 1)D convolution.
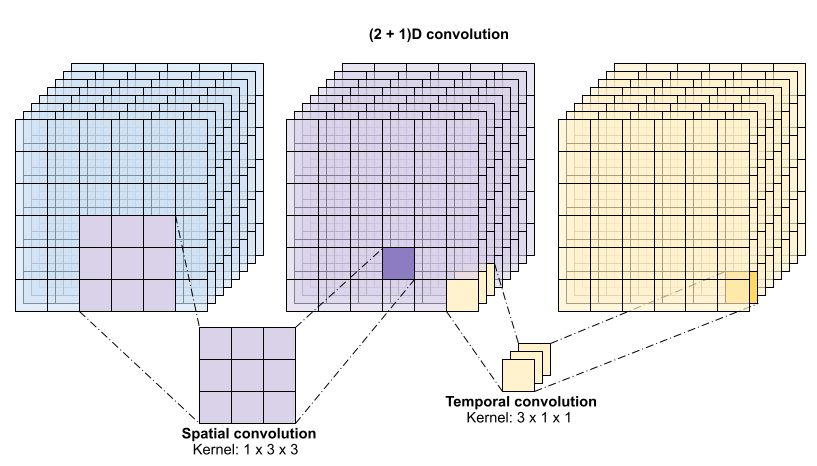
The main advantage of this approach is that it reduces the number of parameters. In the (2 + 1)D convolution the spatial convolution takes in data of the shape (1, width, height), while the temporal convolution takes in data of the shape (time, 1, 1). For example, a (2 + 1)D convolution with kernel size (3 x 3 x 3) would need weight matrices of size (9 * channels**2) + (3 * channels**2), less than half as many as the full 3D convolution. This tutorial implements (2 + 1)D ResNet18, where each convolution in the resnet is replaced by a (2+1)D convolution.
# Define the dimensions of one frame in the set of frames created
HEIGHT = 224
WIDTH = 224
class Conv2Plus1D(keras.layers.Layer):
def __init__(self, filters, kernel_size, padding):
"""
A sequence of convolutional layers that first apply the convolution operation over the
spatial dimensions, and then the temporal dimension.
"""
super().__init__()
self.seq = keras.Sequential([
# Spatial decomposition
layers.Conv3D(filters=filters,
kernel_size=(1, kernel_size[1], kernel_size[2]),
padding=padding),
# Temporal decomposition
layers.Conv3D(filters=filters,
kernel_size=(kernel_size[0], 1, 1),
padding=padding)
])
def call(self, x):
return self.seq(x)
A ResNet model is made from a sequence of residual blocks. A residual block has two branches. The main branch performs the calculation, but is difficult for gradients to flow through. The residual branch bypasses the main calculation and mostly just adds the input to the output of the main branch. Gradients flow easily through this branch. Therefore, an easy path from the loss function to any of the residual block's main branch will be present. This avoids the vanishing gradient problem.
Create the main branch of the residual block with the following class. In contrast to the standard ResNet structure this uses the custom Conv2Plus1D layer instead of layers.Conv2D.
class ResidualMain(keras.layers.Layer):
"""
Residual block of the model with convolution, layer normalization, and the
activation function, ReLU.
"""
def __init__(self, filters, kernel_size):
super().__init__()
self.seq = keras.Sequential([
Conv2Plus1D(filters=filters,
kernel_size=kernel_size,
padding='same'),
layers.LayerNormalization(),
layers.ReLU(),
Conv2Plus1D(filters=filters,
kernel_size=kernel_size,
padding='same'),
layers.LayerNormalization()
])
def call(self, x):
return self.seq(x)
To add the residual branch to the main branch it needs to have the same size. The Project layer below deals with cases where the number of channels is changed on the branch. In particular, a sequence of densely-connected layer followed by normalization is added.
class Project(keras.layers.Layer):
"""
Project certain dimensions of the tensor as the data is passed through different
sized filters and downsampled.
"""
def __init__(self, units):
super().__init__()
self.seq = keras.Sequential([
layers.Dense(units),
layers.LayerNormalization()
])
def call(self, x):
return self.seq(x)
Use add_residual_block to introduce a skip connection between the layers of the model.
def add_residual_block(input, filters, kernel_size):
"""
Add residual blocks to the model. If the last dimensions of the input data
and filter size does not match, project it such that last dimension matches.
"""
out = ResidualMain(filters,
kernel_size)(input)
res = input
# Using the Keras functional APIs, project the last dimension of the tensor to
# match the new filter size
if out.shape[-1] != input.shape[-1]:
res = Project(out.shape[-1])(res)
return layers.add([res, out])
Resizing the video is necessary to perform downsampling of the data. In particular, downsampling the video frames allow for the model to examine specific parts of frames to detect patterns that may be specific to a certain action. Through downsampling, non-essential information can be discarded. Moreoever, resizing the video will allow for dimensionality reduction and therefore faster processing through the model.
class ResizeVideo(keras.layers.Layer):
def __init__(self, height, width):
super().__init__()
self.height = height
self.width = width
self.resizing_layer = layers.Resizing(self.height, self.width)
def call(self, video):
"""
Use the einops library to resize the tensor.
Args:
video: Tensor representation of the video, in the form of a set of frames.
Return:
A downsampled size of the video according to the new height and width it should be resized to.
"""
# b stands for batch size, t stands for time, h stands for height,
# w stands for width, and c stands for the number of channels.
old_shape = einops.parse_shape(video, 'b t h w c')
images = einops.rearrange(video, 'b t h w c -> (b t) h w c')
images = self.resizing_layer(images)
videos = einops.rearrange(
images, '(b t) h w c -> b t h w c',
t = old_shape['t'])
return videos
Use the Keras functional API to build the residual network.
input_shape = (None, 10, HEIGHT, WIDTH, 3)
input = layers.Input(shape=(input_shape[1:]))
x = input
x = Conv2Plus1D(filters=16, kernel_size=(3, 7, 7), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = ResizeVideo(HEIGHT // 2, WIDTH // 2)(x)
# Block 1
x = add_residual_block(x, 16, (3, 3, 3))
x = ResizeVideo(HEIGHT // 4, WIDTH // 4)(x)
# Block 2
x = add_residual_block(x, 32, (3, 3, 3))
x = ResizeVideo(HEIGHT // 8, WIDTH // 8)(x)
# Block 3
x = add_residual_block(x, 64, (3, 3, 3))
x = ResizeVideo(HEIGHT // 16, WIDTH // 16)(x)
# Block 4
x = add_residual_block(x, 128, (3, 3, 3))
x = layers.GlobalAveragePooling3D()(x)
x = layers.Flatten()(x)
x = layers.Dense(10)(x)
model = keras.Model(input, x)
frames, label = next(iter(train_ds))
model.build(frames)
# Visualize the model
keras.utils.plot_model(model, expand_nested=True, dpi=60, show_shapes=True)
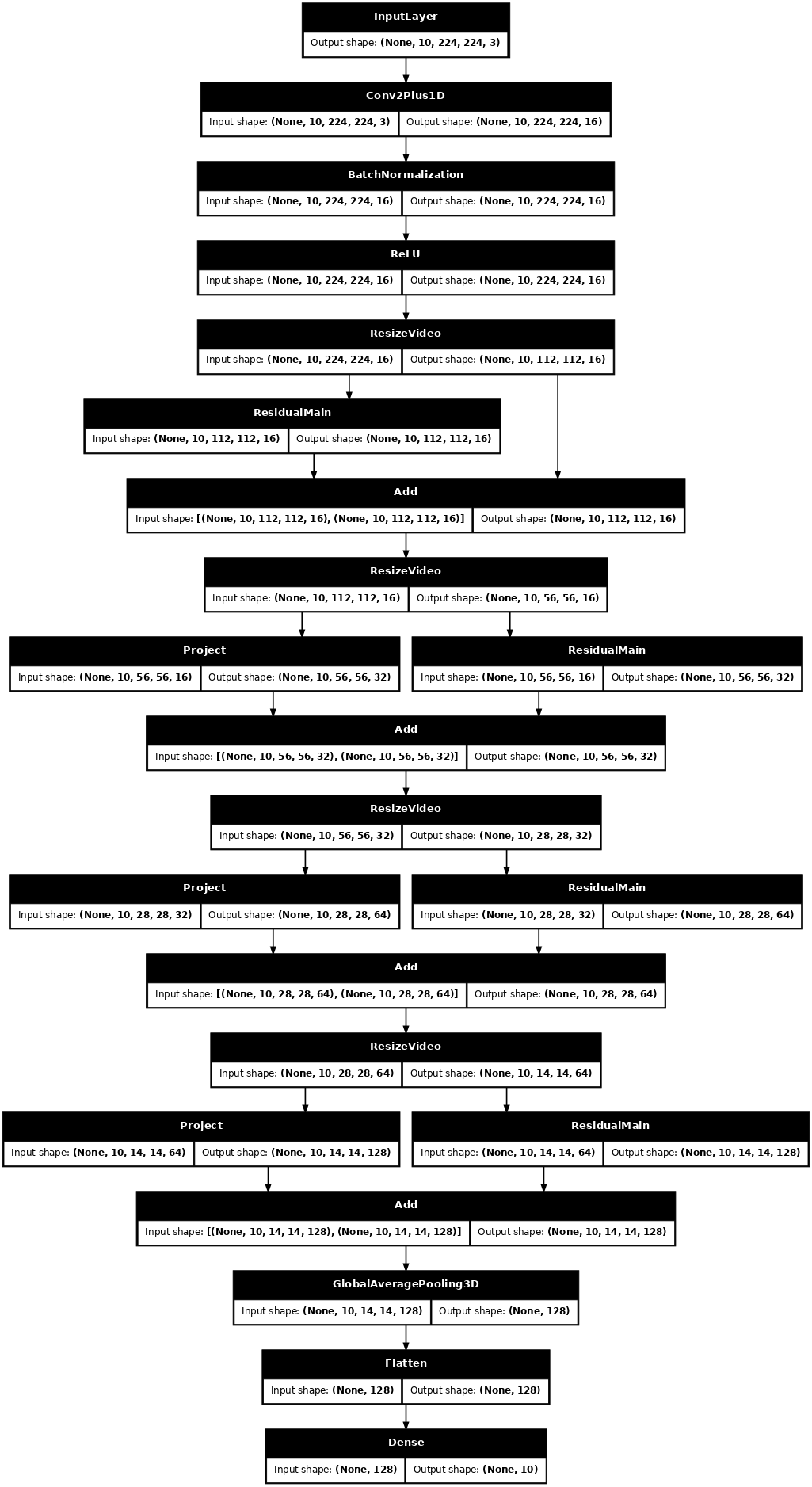
Train the model
For this tutorial, choose the tf.keras.optimizers.Adam optimizer and the tf.keras.losses.SparseCategoricalCrossentropy loss function. Use the metrics argument to the view the accuracy of the model performance at every step.
model.compile(loss = keras.losses.SparseCategoricalCrossentropy(from_logits=True),
optimizer = keras.optimizers.Adam(learning_rate = 0.0001),
metrics = ['accuracy'])
Train the model for 50 epoches with the Keras Model.fit method.
history = model.fit(x = train_ds,
epochs = 50,
validation_data = val_ds)
Epoch 1/50 WARNING: All log messages before absl::InitializeLog() is called are written to STDERR I0000 00:00:1721373662.249732 256020 service.cc:146] XLA service 0x7f3b5c237c40 initialized for platform CUDA (this does not guarantee that XLA will be used). Devices: I0000 00:00:1721373662.249768 256020 service.cc:154] StreamExecutor device (0): Tesla T4, Compute Capability 7.5 I0000 00:00:1721373662.249772 256020 service.cc:154] StreamExecutor device (1): Tesla T4, Compute Capability 7.5 I0000 00:00:1721373662.249775 256020 service.cc:154] StreamExecutor device (2): Tesla T4, Compute Capability 7.5 I0000 00:00:1721373662.249778 256020 service.cc:154] StreamExecutor device (3): Tesla T4, Compute Capability 7.5 I0000 00:00:1721373681.924925 256020 device_compiler.h:188] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process. 38/Unknown 84s 1s/step - accuracy: 0.1530 - loss: 2.5753 /usr/lib/python3.9/contextlib.py:137: UserWarning: Your input ran out of data; interrupting training. Make sure that your dataset or generator can generate at least `steps_per_epoch * epochs` batches. You may need to use the `.repeat()` function when building your dataset. self.gen.throw(typ, value, traceback) 38/38 ━━━━━━━━━━━━━━━━━━━━ 99s 2s/step - accuracy: 0.1529 - loss: 2.5725 - val_accuracy: 0.1100 - val_loss: 2.3406 Epoch 2/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.1664 - loss: 2.1968 - val_accuracy: 0.0900 - val_loss: 2.6421 Epoch 3/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.2190 - loss: 2.1016 - val_accuracy: 0.1700 - val_loss: 2.4371 Epoch 4/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.3174 - loss: 1.9500 - val_accuracy: 0.1500 - val_loss: 2.6620 Epoch 5/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.2943 - loss: 1.8625 - val_accuracy: 0.2600 - val_loss: 2.3139 Epoch 6/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.4187 - loss: 1.7957 - val_accuracy: 0.2300 - val_loss: 2.4179 Epoch 7/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.3722 - loss: 1.7741 - val_accuracy: 0.1500 - val_loss: 2.6977 Epoch 8/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.3890 - loss: 1.6332 - val_accuracy: 0.3000 - val_loss: 2.2304 Epoch 9/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.4238 - loss: 1.5648 - val_accuracy: 0.2900 - val_loss: 2.2203 Epoch 10/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.4779 - loss: 1.4268 - val_accuracy: 0.3600 - val_loss: 1.9324 Epoch 11/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.4449 - loss: 1.5055 - val_accuracy: 0.4500 - val_loss: 1.8140 Epoch 12/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.4654 - loss: 1.4355 - val_accuracy: 0.3400 - val_loss: 2.5344 Epoch 13/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.4088 - loss: 1.4789 - val_accuracy: 0.3000 - val_loss: 1.8802 Epoch 14/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.4777 - loss: 1.3032 - val_accuracy: 0.3700 - val_loss: 2.0959 Epoch 15/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.4911 - loss: 1.3883 - val_accuracy: 0.3600 - val_loss: 1.9853 Epoch 16/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.5455 - loss: 1.2817 - val_accuracy: 0.3300 - val_loss: 1.7012 Epoch 17/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.5350 - loss: 1.2412 - val_accuracy: 0.4200 - val_loss: 1.6499 Epoch 18/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.5554 - loss: 1.1806 - val_accuracy: 0.3500 - val_loss: 1.8051 Epoch 19/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.5136 - loss: 1.2605 - val_accuracy: 0.4000 - val_loss: 1.5037 Epoch 20/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.6112 - loss: 1.1122 - val_accuracy: 0.4700 - val_loss: 1.7054 Epoch 21/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.5933 - loss: 1.0630 - val_accuracy: 0.4600 - val_loss: 1.5221 Epoch 22/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.6262 - loss: 1.0238 - val_accuracy: 0.4600 - val_loss: 1.5333 Epoch 23/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.5820 - loss: 1.1724 - val_accuracy: 0.3300 - val_loss: 1.8660 Epoch 24/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.5783 - loss: 1.1162 - val_accuracy: 0.4700 - val_loss: 1.4044 Epoch 25/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.7091 - loss: 0.9013 - val_accuracy: 0.5100 - val_loss: 1.4534 Epoch 26/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.6638 - loss: 0.9325 - val_accuracy: 0.5300 - val_loss: 1.4975 Epoch 27/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.6634 - loss: 0.8663 - val_accuracy: 0.5400 - val_loss: 1.4653 Epoch 28/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.6904 - loss: 0.8265 - val_accuracy: 0.4200 - val_loss: 1.8303 Epoch 29/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.5707 - loss: 1.1280 - val_accuracy: 0.4900 - val_loss: 1.5225 Epoch 30/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.6606 - loss: 0.8902 - val_accuracy: 0.5000 - val_loss: 1.4556 Epoch 31/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.6940 - loss: 0.8304 - val_accuracy: 0.5100 - val_loss: 1.4460 Epoch 32/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.7436 - loss: 0.6931 - val_accuracy: 0.5000 - val_loss: 1.6054 Epoch 33/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.7498 - loss: 0.7293 - val_accuracy: 0.4700 - val_loss: 1.4887 Epoch 34/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.6699 - loss: 0.9258 - val_accuracy: 0.5300 - val_loss: 1.3688 Epoch 35/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.7091 - loss: 0.7645 - val_accuracy: 0.5800 - val_loss: 1.2813 Epoch 36/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.7307 - loss: 0.7253 - val_accuracy: 0.5500 - val_loss: 1.2997 Epoch 37/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.7196 - loss: 0.7419 - val_accuracy: 0.5100 - val_loss: 1.3091 Epoch 38/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.7863 - loss: 0.6601 - val_accuracy: 0.6200 - val_loss: 1.2057 Epoch 39/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.8253 - loss: 0.5486 - val_accuracy: 0.5200 - val_loss: 1.3492 Epoch 40/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.7529 - loss: 0.6489 - val_accuracy: 0.4900 - val_loss: 1.3248 Epoch 41/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.7441 - loss: 0.6831 - val_accuracy: 0.6100 - val_loss: 1.1946 Epoch 42/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.7692 - loss: 0.5997 - val_accuracy: 0.5500 - val_loss: 1.3455 Epoch 43/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.8137 - loss: 0.5658 - val_accuracy: 0.5400 - val_loss: 1.2936 Epoch 44/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.8258 - loss: 0.5540 - val_accuracy: 0.6400 - val_loss: 1.1666 Epoch 45/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.7656 - loss: 0.6396 - val_accuracy: 0.5300 - val_loss: 1.6629 Epoch 46/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.7373 - loss: 0.6388 - val_accuracy: 0.5400 - val_loss: 1.1805 Epoch 47/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 48s 1s/step - accuracy: 0.7965 - loss: 0.5700 - val_accuracy: 0.4800 - val_loss: 1.7715 Epoch 48/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.6826 - loss: 0.6591 - val_accuracy: 0.5800 - val_loss: 1.1737 Epoch 49/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.8015 - loss: 0.5199 - val_accuracy: 0.6000 - val_loss: 1.1441 Epoch 50/50 38/38 ━━━━━━━━━━━━━━━━━━━━ 49s 1s/step - accuracy: 0.8293 - loss: 0.4492 - val_accuracy: 0.5800 - val_loss: 1.2366
Visualize the results
Create plots of the loss and accuracy on the training and validation sets:
def plot_history(history):
"""
Plotting training and validation learning curves.
Args:
history: model history with all the metric measures
"""
fig, (ax1, ax2) = plt.subplots(2)
fig.set_size_inches(18.5, 10.5)
# Plot loss
ax1.set_title('Loss')
ax1.plot(history.history['loss'], label = 'train')
ax1.plot(history.history['val_loss'], label = 'test')
ax1.set_ylabel('Loss')
# Determine upper bound of y-axis
max_loss = max(history.history['loss'] + history.history['val_loss'])
ax1.set_ylim([0, np.ceil(max_loss)])
ax1.set_xlabel('Epoch')
ax1.legend(['Train', 'Validation'])
# Plot accuracy
ax2.set_title('Accuracy')
ax2.plot(history.history['accuracy'], label = 'train')
ax2.plot(history.history['val_accuracy'], label = 'test')
ax2.set_ylabel('Accuracy')
ax2.set_ylim([0, 1])
ax2.set_xlabel('Epoch')
ax2.legend(['Train', 'Validation'])
plt.show()
plot_history(history)
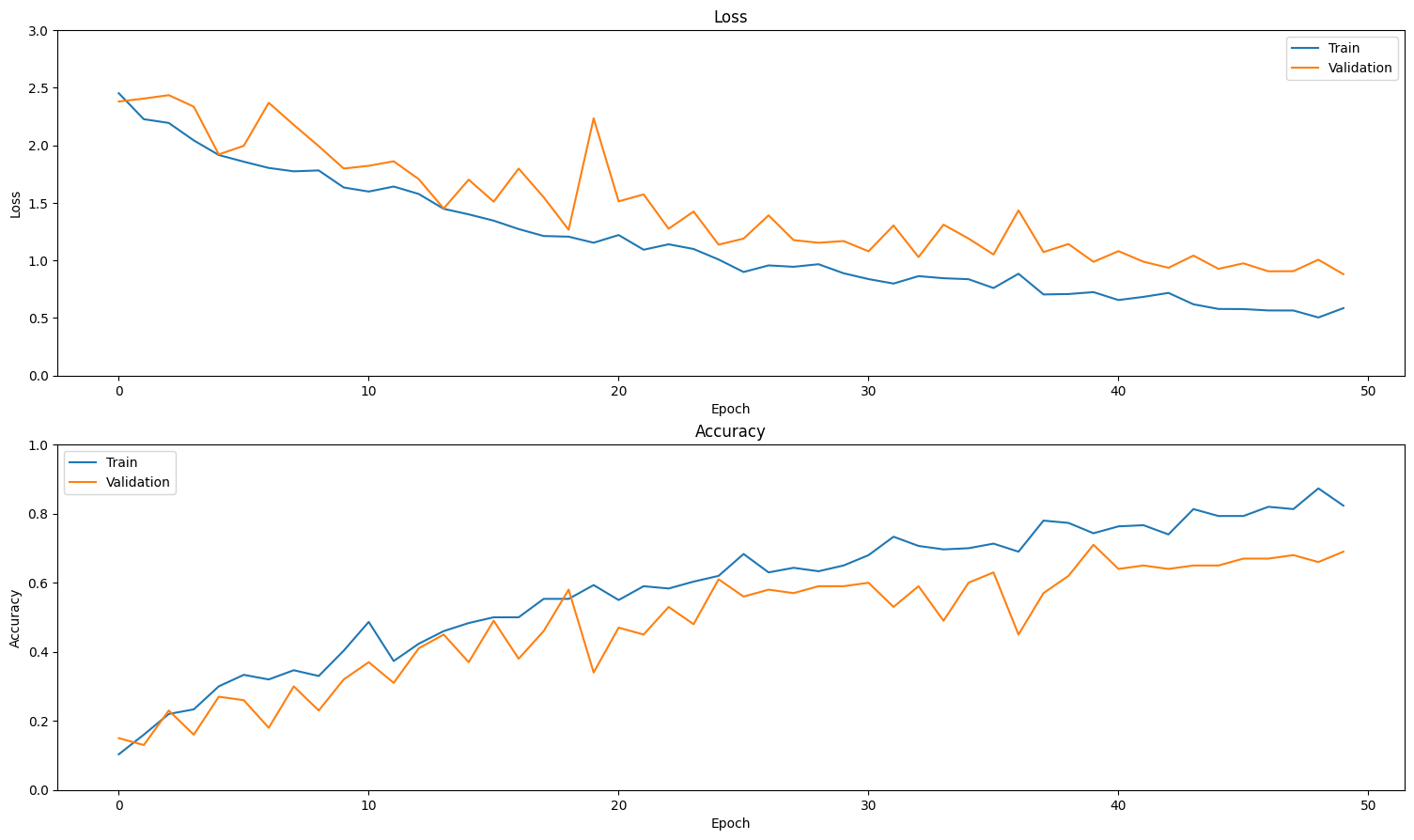
Evaluate the model
Use Keras Model.evaluate to get the loss and accuracy on the test dataset.
model.evaluate(test_ds, return_dict=True)
13/13 ━━━━━━━━━━━━━━━━━━━━ 11s 811ms/step - accuracy: 0.6040 - loss: 1.1950
{'accuracy': 0.6899999976158142, 'loss': 0.9028788208961487}
To visualize model performance further, use a confusion matrix. The confusion matrix allows you to assess the performance of the classification model beyond accuracy. In order to build the confusion matrix for this multi-class classification problem, get the actual values in the test set and the predicted values.
def get_actual_predicted_labels(dataset):
"""
Create a list of actual ground truth values and the predictions from the model.
Args:
dataset: An iterable data structure, such as a TensorFlow Dataset, with features and labels.
Return:
Ground truth and predicted values for a particular dataset.
"""
actual = [labels for _, labels in dataset.unbatch()]
predicted = model.predict(dataset)
actual = tf.stack(actual, axis=0)
predicted = tf.concat(predicted, axis=0)
predicted = tf.argmax(predicted, axis=1)
return actual, predicted
def plot_confusion_matrix(actual, predicted, labels, ds_type):
cm = tf.math.confusion_matrix(actual, predicted)
ax = sns.heatmap(cm, annot=True, fmt='g')
sns.set(rc={'figure.figsize':(12, 12)})
sns.set(font_scale=1.4)
ax.set_title('Confusion matrix of action recognition for ' + ds_type)
ax.set_xlabel('Predicted Action')
ax.set_ylabel('Actual Action')
plt.xticks(rotation=90)
plt.yticks(rotation=0)
ax.xaxis.set_ticklabels(labels)
ax.yaxis.set_ticklabels(labels)
fg = FrameGenerator(subset_paths['train'], n_frames, training=True)
labels = list(fg.class_ids_for_name.keys())
actual, predicted = get_actual_predicted_labels(train_ds)
plot_confusion_matrix(actual, predicted, labels, 'training')
38/38 ━━━━━━━━━━━━━━━━━━━━ 35s 866ms/step
actual, predicted = get_actual_predicted_labels(test_ds)
plot_confusion_matrix(actual, predicted, labels, 'test')
13/13 ━━━━━━━━━━━━━━━━━━━━ 11s 836ms/step /usr/lib/python3.9/contextlib.py:137: UserWarning: Your input ran out of data; interrupting training. Make sure that your dataset or generator can generate at least `steps_per_epoch * epochs` batches. You may need to use the `.repeat()` function when building your dataset. self.gen.throw(typ, value, traceback)
The precision and recall values for each class can also be calculated using a confusion matrix.
def calculate_classification_metrics(y_actual, y_pred, labels):
"""
Calculate the precision and recall of a classification model using the ground truth and
predicted values.
Args:
y_actual: Ground truth labels.
y_pred: Predicted labels.
labels: List of classification labels.
Return:
Precision and recall measures.
"""
cm = tf.math.confusion_matrix(y_actual, y_pred)
tp = np.diag(cm) # Diagonal represents true positives
precision = dict()
recall = dict()
for i in range(len(labels)):
col = cm[:, i]
fp = np.sum(col) - tp[i] # Sum of column minus true positive is false negative
row = cm[i, :]
fn = np.sum(row) - tp[i] # Sum of row minus true positive, is false negative
precision[labels[i]] = tp[i] / (tp[i] + fp) # Precision
recall[labels[i]] = tp[i] / (tp[i] + fn) # Recall
return precision, recall
precision, recall = calculate_classification_metrics(actual, predicted, labels) # Test dataset
precision
{'ApplyEyeMakeup': 0.75,
'ApplyLipstick': 0.6923076923076923,
'Archery': 1.0,
'BabyCrawling': 0.5555555555555556,
'BalanceBeam': 0.7272727272727273,
'BandMarching': 0.8888888888888888,
'BaseballPitch': 0.8,
'Basketball': 0.4117647058823529,
'BasketballDunk': 0.8,
'BenchPress': 0.6666666666666666}
recall
{'ApplyEyeMakeup': 0.6,
'ApplyLipstick': 0.9,
'Archery': 0.1,
'BabyCrawling': 0.5,
'BalanceBeam': 0.8,
'BandMarching': 0.8,
'BaseballPitch': 0.8,
'Basketball': 0.7,
'BasketballDunk': 0.8,
'BenchPress': 0.8}
Next steps
To learn more about working with video data in TensorFlow, check out the following tutorials: