 TensorFlow.org で表示
|
 Google Colab で実行
|
 GitHub でソースを表示
|
 ノートブックをダウンロード
|
いつものように、この例のプログラムは tf.keras APIを使用します。詳しくは TensorFlow の Keras ガイドを参照してください。
これまでの例、つまり、映画レビューの分類と燃費の推定では、検証用データでのモデルの精度が、数エポックでピークを迎え、その後低下するという現象が見られました。
言い換えると、モデルがトレーニング用データを過学習したと考えられます。過学習への対処の仕方を学ぶことは重要です。トレーニング用データセットで高い精度を達成することは難しくありませんが、（これまで見たこともない）テスト用データに汎化したモデルを開発したいのです。
過学習の反対語は学習不足（underfitting）です。学習不足は、モデルがテストデータに対してまだ改善の余地がある場合に発生します。学習不足の原因は様々です。モデルが十分強力でないとか、正則化のしすぎだとか、単にトレーニング時間が短すぎるといった理由があります。学習不足は、トレーニング用データの中の関連したパターンを学習しきっていないということを意味します。
モデルのトレーニングをやりすぎると、モデルは過学習を始め、トレーニング用データの中のパターンで、テストデータには一般的ではないパターンを学習します。そのため、過学習と学習不足の中間を目指す必要があります。これから見ていくように、ちょうどよいエポック数だけトレーニングを行う必要があります。
過学習を防止するための、最良の解決策は、より多くのトレーニング用データを使うことです。データセットには、モデルが処理するあらゆる入力が含まれる必要があります。追加のデータは、新しく興味深いケースに対応する場合にのみ役立ちます。
多くのデータでトレーニングを行えば行うほど、当然のことながらモデルの汎化性能が高くなります。これが不可能な場合、次善の策は正則化のようなテクニックを使うことです。正則化は、モデルに保存される情報の量とタイプに制約をを課します。ネットワークが少数のパターンしか記憶できない場合、最適化プロセスにより、最も顕著なパターンに焦点を合わせるように強制されます。これにより、汎化性能が高くなる可能性があります。
このノートブックでは、いくつかの一般的な正則化手法を使用して分類モデルを改善する方法を見ていきます。
セットアップ
まず、必要なパッケージをインポートします。
import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras import regularizers
print(tf.__version__)
2022-08-09 01:34:49.692956: E tensorflow/stream_executor/cuda/cuda_blas.cc:2981] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered 2022-08-09 01:34:50.411618: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer.so.7'; dlerror: libnvrtc.so.11.1: cannot open shared object file: No such file or directory 2022-08-09 01:34:50.411863: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer_plugin.so.7'; dlerror: libnvrtc.so.11.1: cannot open shared object file: No such file or directory 2022-08-09 01:34:50.411876: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Cannot dlopen some TensorRT libraries. If you would like to use Nvidia GPU with TensorRT, please make sure the missing libraries mentioned above are installed properly. 2.10.0-rc0
!pip install git+https://github.com/tensorflow/docs
import tensorflow_docs as tfdocs
import tensorflow_docs.modeling
import tensorflow_docs.plots
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import pathlib
import shutil
import tempfile
logdir = pathlib.Path(tempfile.mkdtemp())/"tensorboard_logs"
shutil.rmtree(logdir, ignore_errors=True)
Higgs データセット
このチュートリアルの目的は素粒子物理学を行うことではないので、データセットの詳細にこだわる必要はありませんが、これには 11,000,000 のサンプルが含まれていて、各サンプルには 28 の特徴量とバイナリクラスラベルがあります。
gz = tf.keras.utils.get_file('HIGGS.csv.gz', 'http://mlphysics.ics.uci.edu/data/higgs/HIGGS.csv.gz')
Downloading data from http://mlphysics.ics.uci.edu/data/higgs/HIGGS.csv.gz 2816407858/2816407858 [==============================] - 59s 0us/step
FEATURES = 28
tf.data.experimental.CsvDataset クラスを使用すると、中間の解凍手順なしで、gzip ファイルから直接 csv レコードを読み取ることができます。
ds = tf.data.experimental.CsvDataset(gz,[float(),]*(FEATURES+1), compression_type="GZIP")
csv リーダークラスは、各レコードのスカラーのリストを返します。次の関数は、そのスカラーのリストを (feature_vector, label) ペアに再度パックします。
def pack_row(*row):
label = row[0]
features = tf.stack(row[1:],1)
return features, label
TensorFlow は、大規模なバッチのデータで演算する場合に最も効率的です。
したがって、各行を個別に再パックする代わりに、10,000 サンプルのバッチを取得する新しい Dataset を作成し、pack_row 関数を各バッチに適用してから、バッチを個々のレコードに分割します。
packed_ds = ds.batch(10000).map(pack_row).unbatch()
この新しい packed_ds のレコードのいくつかを確認します。
特徴は完全に正規化されていませんが、このチュートリアルには十分です。
for features,label in packed_ds.batch(1000).take(1):
print(features[0])
plt.hist(features.numpy().flatten(), bins = 101)
tf.Tensor( [ 0.8692932 -0.6350818 0.22569026 0.32747006 -0.6899932 0.75420225 -0.24857314 -1.0920639 0. 1.3749921 -0.6536742 0.9303491 1.1074361 1.1389043 -1.5781983 -1.0469854 0. 0.65792954 -0.01045457 -0.04576717 3.1019614 1.35376 0.9795631 0.97807616 0.92000484 0.72165745 0.98875093 0.87667835], shape=(28,), dtype=float32)
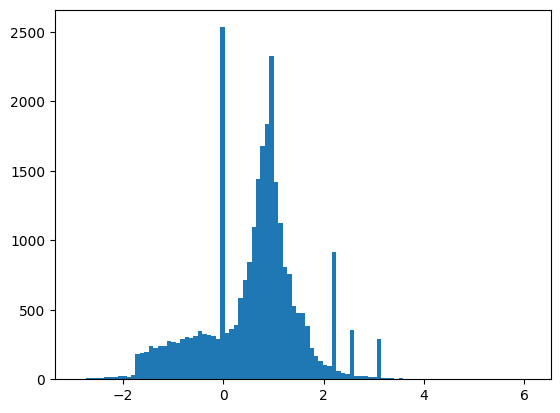
この短いチュートリアルでは、検証に最初の 1,000 サンプルのみを使用し、トレーニングに次の 10,000 サンプルを使用します。
N_VALIDATION = int(1e3)
N_TRAIN = int(1e4)
BUFFER_SIZE = int(1e4)
BATCH_SIZE = 500
STEPS_PER_EPOCH = N_TRAIN//BATCH_SIZE
Dataset.skip と Dataset.take メソッドを使うと簡単に実行できます。
また、Dataset.cache メソッドを使用して、ローダーが各エポックでファイルからデータを再読み取りする必要がないようにします。
validate_ds = packed_ds.take(N_VALIDATION).cache()
train_ds = packed_ds.skip(N_VALIDATION).take(N_TRAIN).cache()
train_ds
<CacheDataset element_spec=(TensorSpec(shape=(28,), dtype=tf.float32, name=None), TensorSpec(shape=(), dtype=tf.float32, name=None))>
これらのデータセットは、個々のサンプルを返します。Dataset.batch メソッドを使用して、トレーニングに適したサイズのバッチを作成します。バッチ処理する前に、トレーニングセットを Dataset.shuffle および Dataset.repeat することも忘れないでください。
validate_ds = validate_ds.batch(BATCH_SIZE)
train_ds = train_ds.shuffle(BUFFER_SIZE).repeat().batch(BATCH_SIZE)
過学習のデモ
過学習を防止するための最も単純な方法は、モデルのサイズ、すなわち、モデル内の学習可能なパラメータの数を小さくすることです（学習パラメータの数は、レイヤーの数とレイヤーごとのユニット数で決まります）。ディープラーニングでは、モデルの学習可能なパラメータ数を、しばしばモデルの「容量」と呼びます。
直感的に考えれば、パラメータ数の多いモデルほど「記憶容量」が大きくなり、トレーニング用のサンプルとその目的変数の間のディクショナリのようなマッピングをたやすく学習することができます。このマッピングには汎化能力がまったくなく、これまで見たことがないデータを使って予測をする際には役に立ちません。
ディープラーニングのモデルはトレーニング用データに適応しやすいけれど、本当のチャレレンジは汎化であって適応ではありません。
一方、ネットワークの記憶容量が限られている場合、前述のようなマッピングを簡単に学習することはできません。損失を減らすためには、より予測能力が高い圧縮された表現を学習しなければなりません。同時に、モデルを小さくしすぎると、トレーニング用データに適応するのが難しくなります。「多すぎる容量」と「容量不足」の間にちょうどよい容量があるのです。
残念ながら、（レイヤーの数や、レイヤーごとの大きさといった）モデルの適切なサイズやアーキテクチャを決める魔法の方程式はありません。一連の異なるアーキテクチャを使って実験を行う必要があります。
適切なモデルのサイズを見つけるには、比較的少ないレイヤーの数とパラメータから始めるのがベストです。それから、検証用データでの損失値の改善が見られなくなるまで、徐々にレイヤーの大きさを増やしたり、新たなレイヤーを加えたりします。
比較基準として、密に接続されたレイヤー（tf.keras.layers.Dense）だけを使ったシンプルなモデルを構築し、その後、大規模なバージョンを作って比較します。
比較基準を作る
トレーニング中に学習率を徐々に下げると、多くのモデルのトレーニングが向上します。tf.keras.optimizers.schedules を使用して、時間の経過とともに学習率を下げます。
lr_schedule = tf.keras.optimizers.schedules.InverseTimeDecay(
0.001,
decay_steps=STEPS_PER_EPOCH*1000,
decay_rate=1,
staircase=False)
def get_optimizer():
return tf.keras.optimizers.Adam(lr_schedule)
上記のコードは、tf.keras.optimizers.schedules.InverseTimeDecay を設定し、学習率を 1000 エポックで基本率の 1/2 に、2000 エポックで 1/3 に双曲線的に減少させます。
step = np.linspace(0,100000)
lr = lr_schedule(step)
plt.figure(figsize = (8,6))
plt.plot(step/STEPS_PER_EPOCH, lr)
plt.ylim([0,max(plt.ylim())])
plt.xlabel('Epoch')
_ = plt.ylabel('Learning Rate')
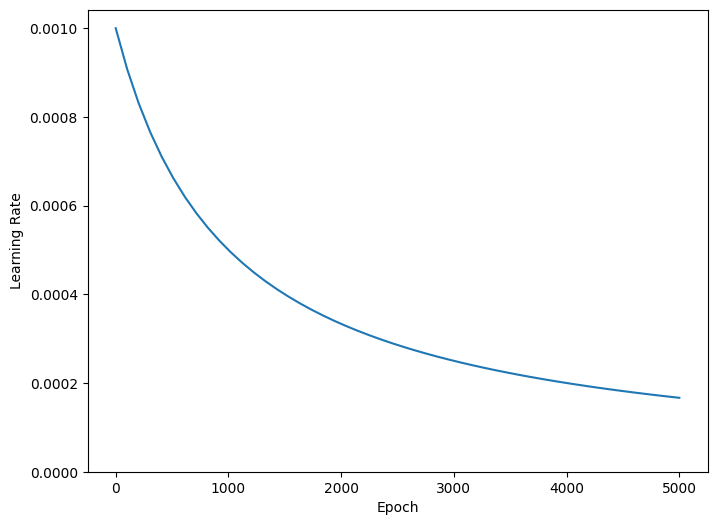
このチュートリアルの各モデルは、同じトレーニング構成を使用します。したがって、コールバックのリストから始めて、再利用可能な方法でこれらを設定します。
このチュートリアルのトレーニングは、多くの短いエポックで実行されます。不要なログ情報を減らすためには、tfdocs.EpochDots を使用します。これは、エポックごとに . を出力し、100 エポックごとにメトリックのフルセットを出力します。
次に、tf.keras.callbacks.EarlyStopping を含めて、トレーニング時間が不必要に長くならないようにます。このコールバックは、val_loss ではなく、val_binary_crossentropy を監視するように設定されていることに注意してください。この違いは後で重要になります。
callbacks.TensorBoard を使用して、トレーニング用の TensorBoard ログを生成します。
def get_callbacks(name):
return [
tfdocs.modeling.EpochDots(),
tf.keras.callbacks.EarlyStopping(monitor='val_binary_crossentropy', patience=200),
tf.keras.callbacks.TensorBoard(logdir/name),
]
同様に、各モデルは同じ Model.compile および Model.fit 設定を使用します。
def compile_and_fit(model, name, optimizer=None, max_epochs=10000):
if optimizer is None:
optimizer = get_optimizer()
model.compile(optimizer=optimizer,
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[
tf.keras.losses.BinaryCrossentropy(
from_logits=True, name='binary_crossentropy'),
'accuracy'])
model.summary()
history = model.fit(
train_ds,
steps_per_epoch = STEPS_PER_EPOCH,
epochs=max_epochs,
validation_data=validate_ds,
callbacks=get_callbacks(name),
verbose=0)
return history
非常に小規模のモデル（Tiny）
まず、モデルをトレーニングします。
tiny_model = tf.keras.Sequential([
layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
layers.Dense(1)
])
size_histories = {}
size_histories['Tiny'] = compile_and_fit(tiny_model, 'sizes/Tiny')
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 16) 464
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 481
Trainable params: 481
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.5012, binary_crossentropy:0.7472, loss:0.7472, val_accuracy:0.5070, val_binary_crossentropy:0.6981, val_loss:0.6981,
....................................................................................................
Epoch: 100, accuracy:0.5962, binary_crossentropy:0.6255, loss:0.6255, val_accuracy:0.5860, val_binary_crossentropy:0.6221, val_loss:0.6221,
....................................................................................................
Epoch: 200, accuracy:0.6227, binary_crossentropy:0.6131, loss:0.6131, val_accuracy:0.6190, val_binary_crossentropy:0.6108, val_loss:0.6108,
....................................................................................................
Epoch: 300, accuracy:0.6435, binary_crossentropy:0.6007, loss:0.6007, val_accuracy:0.6180, val_binary_crossentropy:0.6008, val_loss:0.6008,
....................................................................................................
Epoch: 400, accuracy:0.6584, binary_crossentropy:0.5929, loss:0.5929, val_accuracy:0.6310, val_binary_crossentropy:0.5936, val_loss:0.5936,
....................................................................................................
Epoch: 500, accuracy:0.6690, binary_crossentropy:0.5880, loss:0.5880, val_accuracy:0.6390, val_binary_crossentropy:0.5921, val_loss:0.5921,
....................................................................................................
Epoch: 600, accuracy:0.6688, binary_crossentropy:0.5852, loss:0.5852, val_accuracy:0.6560, val_binary_crossentropy:0.5877, val_loss:0.5877,
....................................................................................................
Epoch: 700, accuracy:0.6695, binary_crossentropy:0.5827, loss:0.5827, val_accuracy:0.6550, val_binary_crossentropy:0.5865, val_loss:0.5865,
....................................................................................................
Epoch: 800, accuracy:0.6756, binary_crossentropy:0.5804, loss:0.5804, val_accuracy:0.6600, val_binary_crossentropy:0.5853, val_loss:0.5853,
....................................................................................................
Epoch: 900, accuracy:0.6798, binary_crossentropy:0.5786, loss:0.5786, val_accuracy:0.6470, val_binary_crossentropy:0.5870, val_loss:0.5870,
....................................................................................................
Epoch: 1000, accuracy:0.6793, binary_crossentropy:0.5774, loss:0.5774, val_accuracy:0.6590, val_binary_crossentropy:0.5862, val_loss:0.5862,
......................................................................................
次に、モデルがどのように機能したかを確認します。
plotter = tfdocs.plots.HistoryPlotter(metric = 'binary_crossentropy', smoothing_std=10)
plotter.plot(size_histories)
plt.ylim([0.5, 0.7])
(0.5, 0.7)
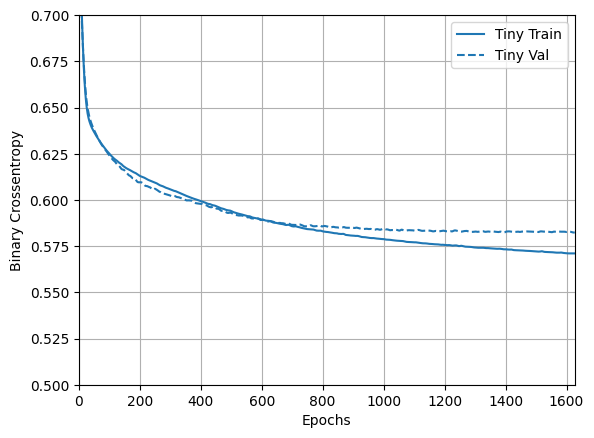
小規模のモデル（Small）
小規模なモデルのパフォーマンスを上回ることができるかどうかを確認するには、いくつかの大規模なモデルを段階的にトレーニングします。
隠れレイヤーが 2 つ、 1 つのレイヤー内のユニットが 16 あるモデルを構築します。
small_model = tf.keras.Sequential([
# `input_shape` is only required here so that `.summary` works.
layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
layers.Dense(16, activation='elu'),
layers.Dense(1)
])
size_histories['Small'] = compile_and_fit(small_model, 'sizes/Small')
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_2 (Dense) (None, 16) 464
dense_3 (Dense) (None, 16) 272
dense_4 (Dense) (None, 1) 17
=================================================================
Total params: 753
Trainable params: 753
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.5041, binary_crossentropy:0.7157, loss:0.7157, val_accuracy:0.4740, val_binary_crossentropy:0.7024, val_loss:0.7024,
....................................................................................................
Epoch: 100, accuracy:0.6303, binary_crossentropy:0.6100, loss:0.6100, val_accuracy:0.6040, val_binary_crossentropy:0.6160, val_loss:0.6160,
....................................................................................................
Epoch: 200, accuracy:0.6664, binary_crossentropy:0.5857, loss:0.5857, val_accuracy:0.6630, val_binary_crossentropy:0.5903, val_loss:0.5903,
....................................................................................................
Epoch: 300, accuracy:0.6743, binary_crossentropy:0.5758, loss:0.5758, val_accuracy:0.6820, val_binary_crossentropy:0.5871, val_loss:0.5871,
....................................................................................................
Epoch: 400, accuracy:0.6811, binary_crossentropy:0.5694, loss:0.5694, val_accuracy:0.6730, val_binary_crossentropy:0.5867, val_loss:0.5867,
....................................................................................................
Epoch: 500, accuracy:0.6828, binary_crossentropy:0.5643, loss:0.5643, val_accuracy:0.6670, val_binary_crossentropy:0.5886, val_loss:0.5886,
....................................................................................................
Epoch: 600, accuracy:0.6882, binary_crossentropy:0.5600, loss:0.5600, val_accuracy:0.6780, val_binary_crossentropy:0.5876, val_loss:0.5876,
...
中規模のモデル（Medium）
次に、隠れレイヤーが 3 つ、 1 つのレイヤー内のユニットが 64 あるモデルを構築します。
medium_model = tf.keras.Sequential([
layers.Dense(64, activation='elu', input_shape=(FEATURES,)),
layers.Dense(64, activation='elu'),
layers.Dense(64, activation='elu'),
layers.Dense(1)
])
同じデータを使って訓練します。
size_histories['Medium'] = compile_and_fit(medium_model, "sizes/Medium")
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_5 (Dense) (None, 64) 1856
dense_6 (Dense) (None, 64) 4160
dense_7 (Dense) (None, 64) 4160
dense_8 (Dense) (None, 1) 65
=================================================================
Total params: 10,241
Trainable params: 10,241
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.4871, binary_crossentropy:0.7102, loss:0.7102, val_accuracy:0.4970, val_binary_crossentropy:0.6888, val_loss:0.6888,
....................................................................................................
Epoch: 100, accuracy:0.7179, binary_crossentropy:0.5234, loss:0.5234, val_accuracy:0.6600, val_binary_crossentropy:0.6028, val_loss:0.6028,
....................................................................................................
Epoch: 200, accuracy:0.7802, binary_crossentropy:0.4354, loss:0.4354, val_accuracy:0.6510, val_binary_crossentropy:0.6874, val_loss:0.6874,
...................................................................
大規模のモデル（Large）
演習として、より大規模なモデルを作成し、それがどれだけ迅速に過適合し始めるかを確認してみましょう。次に、このベンチマークに、ここで必要とされる容量を大幅に上回るネットワークを追加します。
large_model = tf.keras.Sequential([
layers.Dense(512, activation='elu', input_shape=(FEATURES,)),
layers.Dense(512, activation='elu'),
layers.Dense(512, activation='elu'),
layers.Dense(512, activation='elu'),
layers.Dense(1)
])
このモデルもまた同じデータを使って訓練します。
size_histories['large'] = compile_and_fit(large_model, "sizes/large")
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_9 (Dense) (None, 512) 14848
dense_10 (Dense) (None, 512) 262656
dense_11 (Dense) (None, 512) 262656
dense_12 (Dense) (None, 512) 262656
dense_13 (Dense) (None, 1) 513
=================================================================
Total params: 803,329
Trainable params: 803,329
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.5079, binary_crossentropy:0.8317, loss:0.8317, val_accuracy:0.4690, val_binary_crossentropy:0.6976, val_loss:0.6976,
....................................................................................................
Epoch: 100, accuracy:1.0000, binary_crossentropy:0.0023, loss:0.0023, val_accuracy:0.6660, val_binary_crossentropy:1.6926, val_loss:1.6926,
....................................................................................................
Epoch: 200, accuracy:1.0000, binary_crossentropy:0.0001, loss:0.0001, val_accuracy:0.6710, val_binary_crossentropy:2.3084, val_loss:2.3084,
.....................................
訓練時と検証時の損失をグラフにする
実線はトレーニング用データセットの損失、破線は検証用データセットでの損失です（検証用データでの損失が小さい方が良いモデルです）。
より大きなモデルを構築すると、より多くのパワーが得られますが、このパワーが何らかの形で制約されていない場合、トレーニングセットに簡単に過適合する可能性があります。
この例では、通常、"Tiny" モデルのみが過適合を完全に回避し、より大規模なモデルはデータをより迅速に過適合します。過適合は、"large" モデルでは非常に深刻になるため、実際に何が起こっているかを確認するには、プロットを対数スケールに切り替える必要があります。
これは、検証メトリックをトレーニングメトリックとプロットして比較すると明らかです。
- わずかな違いがあるのは正常です。
- 両方のメトリックが同じ方向に移動している場合、すべて正常です。
- トレーニングメトリックが改善し続けているのに検証メトリックが停滞し始めた場合は、おそらく過適合に近づいています。
- 検証メトリックが反対方向に進んでいる場合、モデルは明らかに過適合しています。
plotter.plot(size_histories)
a = plt.xscale('log')
plt.xlim([5, max(plt.xlim())])
plt.ylim([0.5, 0.7])
plt.xlabel("Epochs [Log Scale]")
Text(0.5, 0, 'Epochs [Log Scale]')
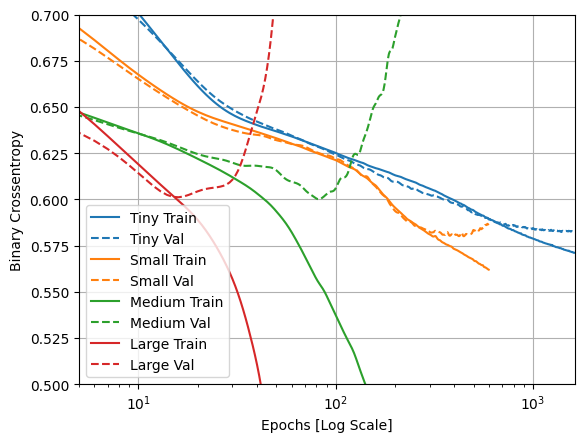
注意: 上記のすべてのトレーニング実行では、callbacks.EarlyStopping を使用して、モデルが進行していないことが明らかになった時点でトレーニングを終了しました。
TensorBoard で表示する
これらのモデルはすべて、トレーニング中に TensorBoard ログを書き込みました。
ノートブック内に埋め込まれた TensorBoard ビューアを開きます。
#docs_infra: no_execute
# Load the TensorBoard notebook extension
%load_ext tensorboard
# Open an embedded TensorBoard viewer
%tensorboard --logdir {logdir}/sizes
TensorBoard.dev で、このノートブックの前回の実行結果を閲覧できます。
TensorBoard.dev は、機械学習の実験をホスト、追跡、および共有するための、マネージドエクスペリエンスです。
便宜上、<iframe> にも含まれています。
display.IFrame(
src="https://tensorboard.dev/experiment/vW7jmmF9TmKmy3rbheMQpw/#scalars&_smoothingWeight=0.97",
width="100%", height="800px")
TensorBoard の結果を共有することを希望する場合は、以下のコードをコードセルに張り付けて、TensorBoard.dev にログをアップロードできます。
注意: Google アカウントが必要です。
tensorboard dev upload --logdir {logdir}/sizes
要注意: このコマンドは終了しません。長時間に及ぶ実験の結果を連続的にアップロードするように設計されています。データのアップロードが完了したら、ノートブックツールの "interrupt execution" オプションを使って停止する必要があります。
過学習防止の戦略
このセクションの内容に入る前に、上記の "Tiny" モデルからトレーニングログをコピーして、比較のベースラインとして使用します。
shutil.rmtree(logdir/'regularizers/Tiny', ignore_errors=True)
shutil.copytree(logdir/'sizes/Tiny', logdir/'regularizers/Tiny')
PosixPath('/tmpfs/tmp/tmpnzx30lyx/tensorboard_logs/regularizers/Tiny')
regularizer_histories = {}
regularizer_histories['Tiny'] = size_histories['Tiny']
重みの正則化を加える
「オッカムの剃刀」の原則をご存知でしょうか。何かの説明が2つあるとすると、最も正しいと考えられる説明は、仮定の数が最も少ない「一番単純な」説明だというものです。この原則は、ニューラルネットワークを使って学習されたモデルにも当てはまります。ある訓練用データとネットワーク構造があって、そのデータを説明できる重みの集合が複数ある時（つまり、複数のモデルがある時）、単純なモデルのほうが複雑なものよりも過学習しにくいのです。
ここで言う「単純なモデル」とは、パラメータ値の分布のエントロピーが小さいもの（あるいは、上記で見たように、そもそもパラメータの数が少ないもの）です。したがって、過学習を緩和するための一般的な手法は、重みが小さい値のみをとることで、重み値の分布がより整然となる（正則）ように制約を与えるものです。これを「重みの正則化」と呼ばれ、ネットワークの損失関数に、重みの大きさに関連するコストを加えることで行われます。このコストには 2 つの種類があります。
L1 正則化: 重み係数の絶対値に比例するコストを加える（重みの「L1 ノルム」と呼ばれる）。
L2 正則化: 重み係数の二乗に比例するコストを加える（重み係数の二乗「L2 ノルム」と呼ばれる）。L2 正則化はニューラルネットワーク用語では重み減衰（Weight Decay）と呼ばれる。呼び方が違うので混乱しないように。重み減衰は数学的には L2 正則化と同義である。
L1 正則化は重みパラメータの一部を 0 にすることでモデルを疎にする効果があります。L2 正則化は重みパラメータにペナルティを加えますがモデルを疎にすることはありません。そのため、L2 正則化のほうが一般的です。
tf.kerasでは、重みの正則化をするために、重み正則化のインスタンスをキーワード引数としてレイヤーに加えます。ここでは、L2 正則化を追加してみましょう。
l2_model = tf.keras.Sequential([
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001),
input_shape=(FEATURES,)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(1)
])
regularizer_histories['l2'] = compile_and_fit(l2_model, "regularizers/l2")
Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_14 (Dense) (None, 512) 14848
dense_15 (Dense) (None, 512) 262656
dense_16 (Dense) (None, 512) 262656
dense_17 (Dense) (None, 512) 262656
dense_18 (Dense) (None, 1) 513
=================================================================
Total params: 803,329
Trainable params: 803,329
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.4994, binary_crossentropy:0.8226, loss:2.3421, val_accuracy:0.5070, val_binary_crossentropy:0.6744, val_loss:2.1193,
....................................................................................................
Epoch: 100, accuracy:0.6396, binary_crossentropy:0.6014, loss:0.6224, val_accuracy:0.5930, val_binary_crossentropy:0.6030, val_loss:0.6239,
....................................................................................................
Epoch: 200, accuracy:0.6750, binary_crossentropy:0.5796, loss:0.6034, val_accuracy:0.6180, val_binary_crossentropy:0.5876, val_loss:0.6113,
....................................................................................................
Epoch: 300, accuracy:0.6817, binary_crossentropy:0.5733, loss:0.5976, val_accuracy:0.6220, val_binary_crossentropy:0.5872, val_loss:0.6112,
....................................................................................................
Epoch: 400, accuracy:0.6879, binary_crossentropy:0.5653, loss:0.5886, val_accuracy:0.6810, val_binary_crossentropy:0.5769, val_loss:0.6001,
..................................................
l2(0.001) というのは、レイヤーの重み行列の係数全てに対して 0.001 * weight_coefficient_value**2 をネットワークの損失値合計に加えることを意味します。
そのため、binary_crossentropy を直接監視しています。この正則化コンポーネントが混在していないためです。
したがって、L2 正則化ペナルティが設けられた同じ "Large" モデルのパフォーマンスははるかに優れています。
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
(0.5, 0.7)
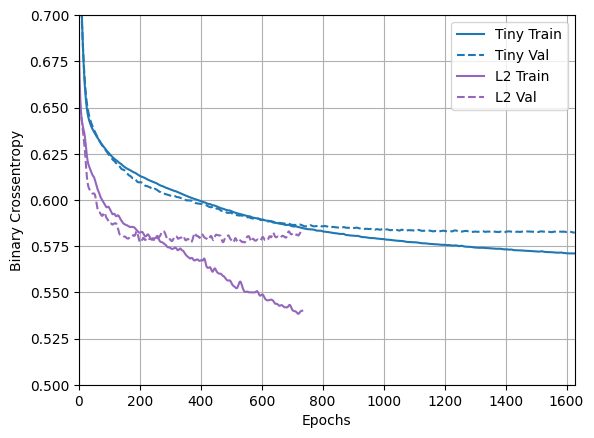
ご覧のように、"L2" 正則化ありのモデルは "Tiny" モデルとほぼ同等になりました。"L2" モデルは "Large" モデルと比べて過学習しにくくなっています。両方のモデルのパラメータ数は同じであるにもかかわらずです。
詳細情報
このような正則化について注意すべき重要事項が 2 つあります。
- 独自のトレーニングループを作成している場合は、モデルに正則化の損失を必ず確認する必要があります。
result = l2_model(features)
regularization_loss=tf.add_n(l2_model.losses)
- この実装は、モデルの損失に対して重みペナルティを与えてから標準の最適化手順を適用します。
2 番目のアプローチでは、代わりに、生の損失に対してのみオプティマイザを実行します。オプティマイザは計算されたステップを適用しながら、重みの減衰も適用します。この「分離された重みの減衰」は、tf.keras.optimizers.Ftrl や tfa.optimizers.AdamW などのオプティマイザで使用されます。
ドロップアウトを追加する
ドロップアウトは、ニューラルネットワークの正則化テクニックとして最もよく使われる手法の一つです。この手法は、トロント大学のヒントンと彼の学生が開発したものです。ドロップアウトは層に適用するもので、訓練時に層から出力された特徴量に対してランダムに「ドロップアウト（つまりゼロ化）」を行うものです。例えば、ある層が訓練時にある入力サンプルに対して、普通は[0.2, 0.5, 1.3, 0.8, 1.1] というベクトルを出力するとします。ドロップアウトを適用すると、このベクトルは例えば[0, 0.5, 1.3, 0, 1.1]のようにランダムに散らばったいくつかのゼロを含むようになります。「ドロップアウト率」はゼロ化される特徴の割合で、通常は0.2から0.5の間に設定します。テスト時は、どのユニットもドロップアウトされず、代わりに出力値がドロップアウト率と同じ比率でスケールダウンされます。これは、訓練時に比べてたくさんのユニットがアクティブであることに対してバランスをとるためです。
ドロップアウトを簡単に説明すると、ネットワーク内の個々のノードは他のノードの出力に依存できないため、各ノードはそれ自体で役立つ特徴を出力する必要があるということです。
ドロップアウトはレイヤーに適用するもので、トレーニング時にレイヤーから出力された特徴量に対してランダムに「ドロップアウト（つまりゼロ化）」を行うものです。例えば、あるレイヤーがトレーニング時にある入力サンプルに対して、普通は[0.2, 0.5, 1.3, 0.8, 1.1] というベクトルを出力するとします。ドロップアウトを適用すると、このベクトルは例えば[0, 0.5, 1.3, 0, 1.1]のようにランダムに散らばったいくつかのゼロを含むようになります。
「ドロップアウト率」はゼロ化される特徴の割合で、通常は 0.2 から 0.5 の間に設定します。テスト時は、どのユニットもドロップアウトされず、代わりに出力値がドロップアウト率と同じ比率でスケールダウンされます。これは、トレーニング時に比べてたくさんのユニットがアクティブであることに対してバランスをとるためです。
Keras では、tf.keras.layers.Dropout レイヤーを使ってドロップアウトをネットワークに導入できます。ドロップアウトレイヤーは、その直前のレイヤーの出力に対してドロップアウトを適用します。
ネットワークに 2 つのドロップアウトレイヤーを追加して、過適合を減らすのにどれだけ効果を発揮するか見てみましょう。
dropout_model = tf.keras.Sequential([
layers.Dense(512, activation='elu', input_shape=(FEATURES,)),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(1)
])
regularizer_histories['dropout'] = compile_and_fit(dropout_model, "regularizers/dropout")
Model: "sequential_5"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_19 (Dense) (None, 512) 14848
dropout (Dropout) (None, 512) 0
dense_20 (Dense) (None, 512) 262656
dropout_1 (Dropout) (None, 512) 0
dense_21 (Dense) (None, 512) 262656
dropout_2 (Dropout) (None, 512) 0
dense_22 (Dense) (None, 512) 262656
dropout_3 (Dropout) (None, 512) 0
dense_23 (Dense) (None, 1) 513
=================================================================
Total params: 803,329
Trainable params: 803,329
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.4986, binary_crossentropy:0.8199, loss:0.8199, val_accuracy:0.4610, val_binary_crossentropy:0.6931, val_loss:0.6931,
....................................................................................................
Epoch: 100, accuracy:0.6550, binary_crossentropy:0.5985, loss:0.5985, val_accuracy:0.6610, val_binary_crossentropy:0.5761, val_loss:0.5761,
....................................................................................................
Epoch: 200, accuracy:0.6958, binary_crossentropy:0.5530, loss:0.5530, val_accuracy:0.6720, val_binary_crossentropy:0.5829, val_loss:0.5829,
....................................................................................................
Epoch: 300, accuracy:0.7230, binary_crossentropy:0.5132, loss:0.5132, val_accuracy:0.6830, val_binary_crossentropy:0.5924, val_loss:0.5924,
...................................
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
(0.5, 0.7)
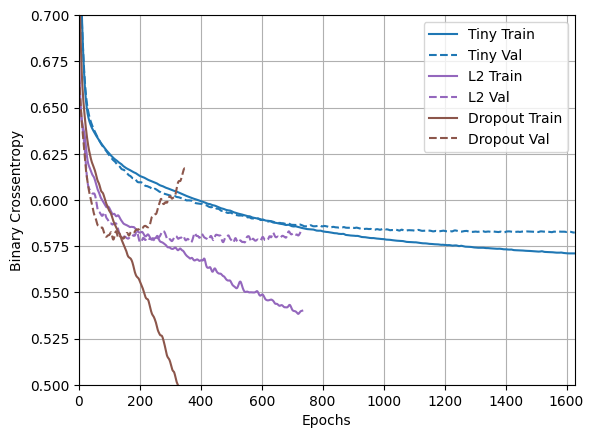
このプロットから、これらの正則化アプローチは両方とも "Large" モデルの動作を改善することが分かります。しかし、"Tiny" のベースラインと比較すると勝るものはありません。
次に、両方を一緒に試して、改善するかどうかを確認します。
L2 とドロップアウトを組み合わせる
combined_model = tf.keras.Sequential([
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu', input_shape=(FEATURES,)),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(1)
])
regularizer_histories['combined'] = compile_and_fit(combined_model, "regularizers/combined")
Model: "sequential_6"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_24 (Dense) (None, 512) 14848
dropout_4 (Dropout) (None, 512) 0
dense_25 (Dense) (None, 512) 262656
dropout_5 (Dropout) (None, 512) 0
dense_26 (Dense) (None, 512) 262656
dropout_6 (Dropout) (None, 512) 0
dense_27 (Dense) (None, 512) 262656
dropout_7 (Dropout) (None, 512) 0
dense_28 (Dense) (None, 1) 513
=================================================================
Total params: 803,329
Trainable params: 803,329
Non-trainable params: 0
_________________________________________________________________
Epoch: 0, accuracy:0.5021, binary_crossentropy:0.7948, loss:0.9534, val_accuracy:0.5140, val_binary_crossentropy:0.6753, val_loss:0.8333,
....................................................................................................
Epoch: 100, accuracy:0.6432, binary_crossentropy:0.6062, loss:0.6359, val_accuracy:0.6190, val_binary_crossentropy:0.5898, val_loss:0.6194,
....................................................................................................
Epoch: 200, accuracy:0.6623, binary_crossentropy:0.5907, loss:0.6167, val_accuracy:0.6860, val_binary_crossentropy:0.5699, val_loss:0.5958,
....................................................................................................
Epoch: 300, accuracy:0.6719, binary_crossentropy:0.5829, loss:0.6115, val_accuracy:0.6810, val_binary_crossentropy:0.5649, val_loss:0.5934,
....................................................................................................
Epoch: 400, accuracy:0.6767, binary_crossentropy:0.5764, loss:0.6070, val_accuracy:0.6730, val_binary_crossentropy:0.5652, val_loss:0.5958,
....................................................................................................
Epoch: 500, accuracy:0.6808, binary_crossentropy:0.5705, loss:0.6034, val_accuracy:0.6790, val_binary_crossentropy:0.5607, val_loss:0.5937,
....................................................................................................
Epoch: 600, accuracy:0.6861, binary_crossentropy:0.5658, loss:0.6005, val_accuracy:0.6840, val_binary_crossentropy:0.5481, val_loss:0.5828,
....................................................................................................
Epoch: 700, accuracy:0.6890, binary_crossentropy:0.5603, loss:0.5968, val_accuracy:0.6950, val_binary_crossentropy:0.5394, val_loss:0.5758,
....................................................................................................
Epoch: 800, accuracy:0.6947, binary_crossentropy:0.5558, loss:0.5939, val_accuracy:0.6970, val_binary_crossentropy:0.5485, val_loss:0.5865,
....................................................................................................
Epoch: 900, accuracy:0.6928, binary_crossentropy:0.5527, loss:0.5922, val_accuracy:0.6930, val_binary_crossentropy:0.5439, val_loss:0.5834,
.............................
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
(0.5, 0.7)
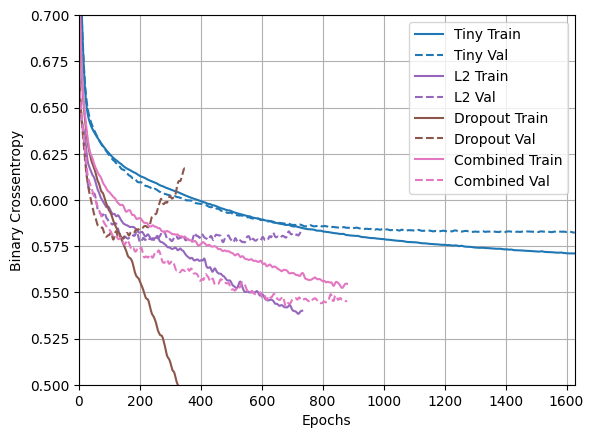
"Combined" 正則化を使用したモデルは、明らかに最も優れたモデルです。
TensorBoard で表示する
これらのモデルは、TensorBoard ログも記録しました。
ノートブック内に埋め込まれたテンソルボードビューアを開くには、以下をコードセルにコピーします。
%tensorboard --logdir {logdir}/regularizers
TensorBoard.dev で、このノートブックの前回の実行結果を閲覧できます。
便宜上、<iframe> にも含まれています。
display.IFrame(
src="https://tensorboard.dev/experiment/fGInKDo8TXes1z7HQku9mw/#scalars&_smoothingWeight=0.97",
width = "100%",
height="800px")
次のようにアップロードされました。
tensorboard dev upload --logdir {logdir}/regularizers
まとめ
ニューラルネットワークの過適合を防ぐための最も一般的な方法は次のとおりです。
- より多くのトレーニングデータを取得します。
- ネットワークの容量を減らします。
- 重みの正則化を追加します。
- ドロップアウトを追加します。
このガイドで説明されていない 2 つの重要なアプローチは次のとおりです。
- データ拡張
- バッチ正規化 (
tf.keras.layers.BatchNormalization)
それぞれの方法は個別に利用しても役立つ可能性がありますが、多くの場合、組み合わせるとさらに効果的になります。
# MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.