 عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
يتضمن دليل مقدمة إلى التدرجات والتمايز التلقائي كل ما هو مطلوب لحساب التدرجات في TensorFlow. يركز هذا الدليل على الميزات الأعمق والأقل شيوعًا لواجهة tf.GradientTape API.
يثبت
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
التحكم في تسجيل التدرج
في دليل التمايز التلقائي ، رأيت كيفية التحكم في المتغيرات والموترات التي يراقبها الشريط أثناء بناء حساب التدرج.
يحتوي الشريط أيضًا على طرق للتعامل مع التسجيل.
إيقاف التسجيل
إذا كنت ترغب في إيقاف تسجيل التدرجات ، يمكنك استخدام tf.GradientTape.stop_recording لتعليق التسجيل مؤقتًا.
قد يكون هذا مفيدًا لتقليل النفقات العامة إذا كنت لا ترغب في التمييز بين عملية معقدة في منتصف النموذج الخاص بك. يمكن أن يشمل ذلك حساب مقياس أو نتيجة وسيطة:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
إعادة تعيين / بدء التسجيل من البداية
إذا كنت ترغب في البدء من جديد بالكامل ، فاستخدم tf.GradientTape.reset . عادةً ما يكون الخروج من كتلة شريط التدرج وإعادة التشغيل أسهل في القراءة ، ولكن يمكنك استخدام طريقة reset عندما يكون الخروج من كتلة الشريط صعبًا أو مستحيلًا.
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all the tape recorded so far.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
وقف تدفق التدرج بدقة
على عكس عناصر التحكم العامة في الشريط أعلاه ، فإن وظيفة tf.stop_gradient أكثر دقة. يمكن استخدامه لإيقاف تدفق التدرجات على طول مسار معين ، دون الحاجة إلى الوصول إلى الشريط نفسه:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
التدرجات المخصصة
في بعض الحالات ، قد ترغب في التحكم بالضبط في كيفية حساب التدرجات بدلاً من استخدام الافتراضي. تشمل هذه المواقف:
- لا يوجد تدرج محدد للعملية الجديدة التي تكتبها.
- الحسابات الافتراضية غير مستقرة عدديًا.
- كنت ترغب في تخزين عملية حسابية باهظة الثمن مؤقتًا من التمرير الأمامي.
- تريد تعديل قيمة (على سبيل المثال ، باستخدام
tf.clip_by_valueأوtf.math.round) بدون تعديل التدرج اللوني.
بالنسبة للحالة الأولى ، لكتابة مرجع جديد ، يمكنك استخدام tf.RegisterGradient لإعداد ملفك الخاص (راجع مستندات API للحصول على التفاصيل). (لاحظ أن سجل التدرج عالمي ، لذا قم بتغييره بحذر.)
للحالات الثلاث الأخيرة ، يمكنك استخدام tf.custom_gradient .
فيما يلي مثال يطبق tf.clip_by_norm على التدرج المتوسط:
# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, shape=(), dtype=float32)
راجع مستندات واجهة برمجة تطبيقات tf.custom_gradient decorator لمزيد من التفاصيل.
التدرجات المخصصة في SavedModel
يمكن حفظ التدرجات المخصصة في SavedModel باستخدام الخيار tf.saved_model.SaveOptions(experimental_custom_gradients=True) .
ليتم حفظها في SavedModel ، يجب أن تكون وظيفة التدرج قابلة للتتبع (لمعرفة المزيد ، تحقق من أفضل أداء مع دليل وظيفة tf ).
class MyModule(tf.Module):
@tf.function(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
model = MyModule()
tf.saved_model.save(
model,
'saved_model',
options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
INFO:tensorflow:Assets written to: saved_model/assets tf.Tensor(2.0, shape=(), dtype=float32)
ملاحظة حول المثال أعلاه: إذا حاولت استبدال الكود أعلاه بـ tf.saved_model.SaveOptions(experimental_custom_gradients=False) ، فسيظل التدرج ينتج نفس النتيجة عند التحميل. والسبب هو أن سجل التدرج لا يزال يحتوي على التدرج المخصص المستخدم في الوظيفة call_custom_op . ومع ذلك ، إذا أعدت تشغيل وقت التشغيل بعد الحفظ بدون تدرجات مخصصة ، فسيؤدي تشغيل النموذج المحمل ضمن tf.GradientTape إلى ظهور الخطأ: خطأ LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .
شرائط متعددة
تتفاعل الأشرطة المتعددة بسلاسة.
على سبيل المثال ، يشاهد كل شريط هنا مجموعة مختلفة من الموترات:
x0 = tf.constant(0.0)
x1 = tf.constant(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
التدرجات العليا
يتم تسجيل العمليات داخل مدير سياق tf.GradientTape للتمييز التلقائي. إذا تم حساب التدرجات في هذا السياق ، فسيتم تسجيل حساب التدرج أيضًا. نتيجة لذلك ، تعمل واجهة برمجة التطبيقات نفسها تمامًا مع التدرجات عالية الترتيب أيضًا.
فمثلا:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient inside the outer `t2` context manager
# which means the gradient computation is differentiable as well.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0 d2y_dx2: 6.0
في حين أن هذا يعطيك المشتق الثاني للدالة العددية ، فإن هذا النمط لا يعمم لإنتاج مصفوفة هسي ، لأن tf.GradientTape.gradient يحسب فقط التدرج اللوني للعددي. لإنشاء مصفوفة Hessian ، انتقل إلى مثال Hessian ضمن القسم Jacobian .
"الاستدعاءات المتداخلة لـ tf.GradientTape.gradient " هي نمط جيد عندما تحسب مقياسًا من التدرج اللوني ، ثم يعمل العدد القياسي الناتج كمصدر لحساب التدرج الثاني ، كما في المثال التالي.
مثال: تسوية التدرج المدخلات
العديد من النماذج عرضة "لأمثلة الخصومة". هذه المجموعة من التقنيات تعدل مدخلات النموذج للتشويش على مخرجات النموذج. أبسط تطبيق - مثل المثال التنافسي باستخدام هجوم أسلوب التدرج السريع الموقّع - يأخذ خطوة واحدة على طول التدرج اللوني للمخرجات فيما يتعلق بالإدخال ؛ "التدرج المدخلات".
تتمثل إحدى تقنيات زيادة المتانة للأمثلة العدائية في تنظيم تدرج الإدخال (Finlay & Oberman ، 2019) ، والذي يحاول تقليل حجم التدرج اللوني للإدخال. إذا كان تدرج الإدخال صغيرًا ، فيجب أن يكون التغيير في الإخراج صغيرًا أيضًا.
يوجد أدناه تنفيذ ساذج لتنظيم تدرج الإدخال. التنفيذ هو:
- احسب تدرج الإخراج بالنسبة للإدخال باستخدام شريط داخلي.
- احسب مقدار هذا التدرج اللوني.
- احسب انحدار هذا المقدار بالنسبة للنموذج.
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The inner tape only takes the gradient with respect to the input,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the input gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the input gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
اليعاقبة
أخذت جميع الأمثلة السابقة تدرجات الهدف القياسي فيما يتعلق ببعض موتر (موترات) المصدر.
تمثل المصفوفة اليعقوبية تدرجات دالة ذات قيمة متجهية. يحتوي كل صف على تدرج أحد عناصر المتجه.
تتيح لك طريقة tf.GradientTape.jacobian حساب مصفوفة يعقوبية بكفاءة.
لاحظ أن:
- مثل
gradient: يمكن أن تكون وسيطةsourcesموترًا أو حاوية من موترات. - على عكس
gradient: يجب أن يكون الموترtargetموترًا واحدًا.
مصدر عددي
كمثال أولي ، هنا جاكوبي لهدف متجه فيما يتعلق بمصدر عددي.
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
عندما تأخذ Jacobian بالنسبة إلى العددية ، يكون للنتيجة شكل الهدف ، وتعطي التدرج اللوني لكل عنصر فيما يتعلق بالمصدر:
print(y.shape)
print(dy_dx.shape)
(201,) (201,)
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
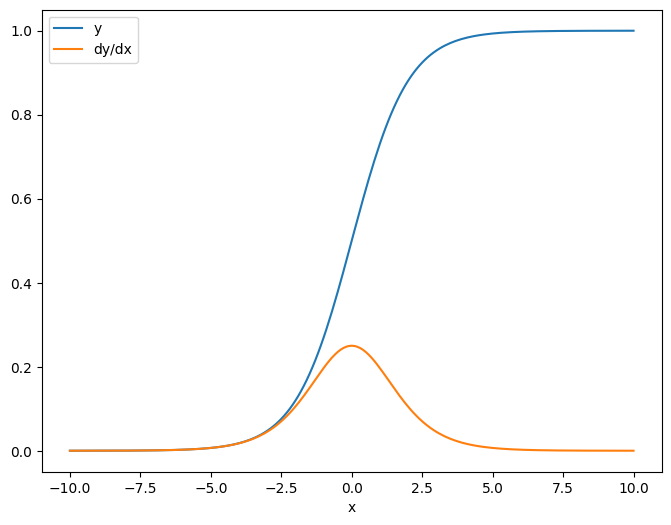
مصدر موتر
سواء كان الإدخال عدديًا أو موترًا ، tf.GradientTape.jacobian يحسب بكفاءة التدرج اللوني لكل عنصر من عناصر المصدر فيما يتعلق بكل عنصر من عناصر الهدف (الأهداف).
على سبيل المثال ، ناتج هذه الطبقة له شكل (10, 7) :
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.shape
TensorShape([7, 10])
وشكل نواة الطبقة هو (5, 10) :
layer.kernel.shape
TensorShape([5, 10])
شكل اليعقوبي الناتج بالنسبة للنواة هو هذين الشكلين المتصلين معًا:
j = tape.jacobian(y, layer.kernel)
j.shape
TensorShape([7, 10, 5, 10])
إذا جمعت أبعاد الهدف ، فسيتبقى لك تدرج المجموع الذي كان سيحسب بواسطة tf.GradientTape.gradient :
g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.shape: (5, 10) delta: 2.3841858e-07
مثال: هسه
بينما لا يعطي tf.GradientTape طريقة واضحة لإنشاء مصفوفة Hessian ، فمن الممكن إنشاء واحدة باستخدام طريقة tf.GradientTape.jacobian .
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')
layer.kernel.shape: (5, 8) h.shape: (5, 8, 5, 8)
لاستخدام هذا Hessian لخطوة طريقة نيوتن ، عليك أولاً تسطيح محاورها في مصفوفة ، وتسوية التدرج إلى متجه:
n_params = tf.reduce_prod(layer1.kernel.shape)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
يجب أن تكون مصفوفة هسه متماثلة:
def imshow_zero_center(image, **kwargs):
lim = tf.reduce_max(abs(image))
plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
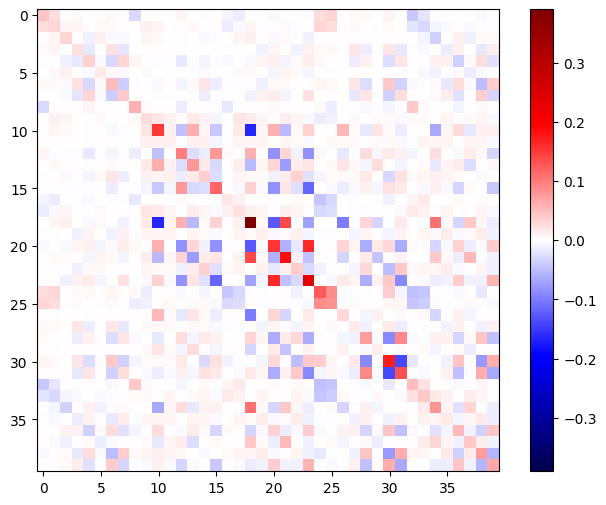
تظهر خطوة تحديث طريقة نيوتن أدناه:
eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps
# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)
# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))
في حين أن هذا بسيط نسبيًا لمتغير tf واحد ، فإن تطبيق هذا على نموذج غير تافه يتطلب tf.Variable دقيقًا لإنتاج Hessian كامل عبر متغيرات متعددة.
باتش جاكوبيان
في بعض الحالات ، تريد أن تأخذ Jacobian لكل مجموعة من الأهداف فيما يتعلق بمجموعة من المصادر ، حيث يكون اليعاقبة لكل زوج من مصادر الهدف مستقلين.
على سبيل المثال ، هنا يتم تشكيل المدخلات x (batch, ins) الناتج y (batch, outs) :
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.shape
TensorShape([7, 6])
جاكوبي الكامل لـ y بالنسبة إلى x له شكل (batch, ins, batch, outs) ، حتى لو كنت تريد فقط (batch, ins, outs) :
j = tape.jacobian(y, x)
j.shape
TensorShape([7, 6, 7, 5])
إذا كانت تدرجات كل عنصر في المكدس مستقلة ، فإن كل شريحة (batch, batch) من هذا الموتر هي مصفوفة قطرية:
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
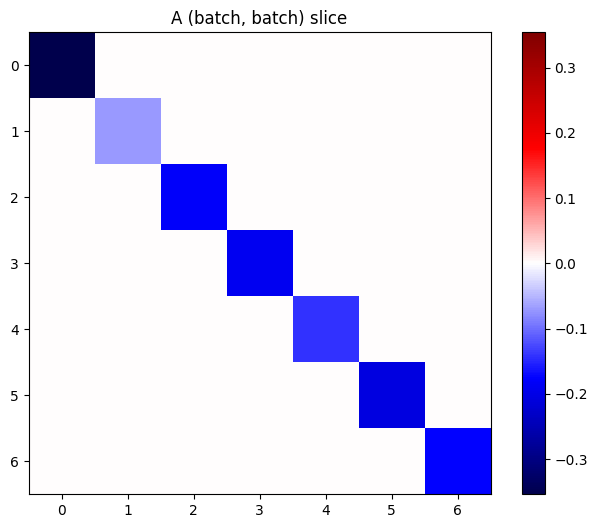
def plot_as_patches(j):
# Reorder axes so the diagonals will each form a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between each patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to form a single image.
s = j.shape
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
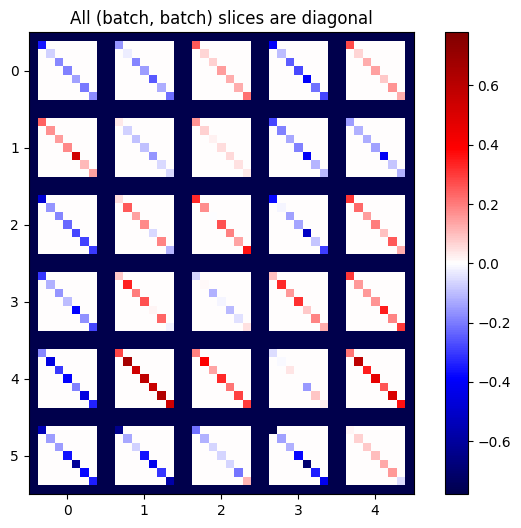
للحصول على النتيجة المرجوة ، يمكنك جمع أبعاد batch المكررة ، أو تحديد الأقطار باستخدام tf.einsum :
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)
(7, 6, 5) (7, 6, 5)
سيكون إجراء الحساب بدون البعد الإضافي أكثر فاعلية في المقام الأول. تقوم طريقة tf.GradientTape.batch_jacobian بما يلي بالضبط:
jb = tape.batch_jacobian(y, x)
jb.shape
WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. TensorShape([7, 6, 5])
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, training=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')
WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. j.shape: (7, 6, 7, 5)
plot_as_patches(j)
_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")
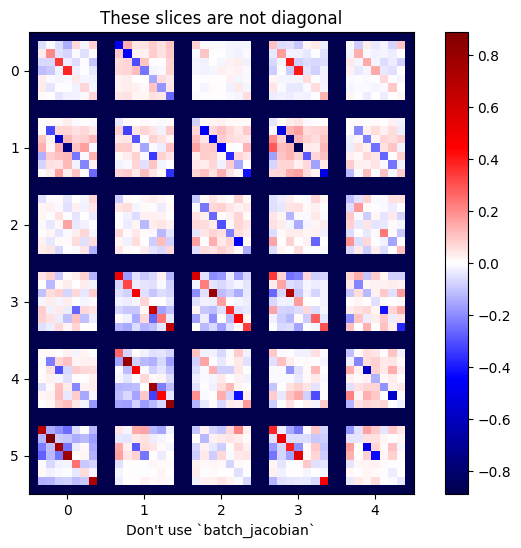
في هذه الحالة ، يستمر تشغيل batch_jacobian وإرجاع شيء ما بالشكل المتوقع ، لكن محتوياته لها معنى غير واضح:
jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')
jb.shape: (7, 6, 5)
