 הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
מדריך המבוא להדרגות והבידול האוטומטי כולל את כל מה שנדרש לחישוב מעברים ב-TensorFlow. מדריך זה מתמקד בתכונות עמוקות יותר ופחות נפוצות של ממשק ה-API של tf.GradientTape .
להכין
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
שליטה בהקלטת שיפוע
במדריך הבידול האוטומטי ראית כיצד לשלוט באילו משתנים וטנסורים נצפים על ידי הקלטת בזמן בניית חישוב הגרדיאנט.
לקלטת יש גם שיטות לתפעל את ההקלטה.
הפסק להקליט
אם ברצונך להפסיק להקליט מעברי צבע, תוכל להשתמש ב- tf.GradientTape.stop_recording כדי להשעות את ההקלטה באופן זמני.
זה עשוי להיות שימושי כדי להפחית את התקורה אם אינך רוצה להבדיל בין פעולה מסובכת באמצע המודל שלך. זה יכול לכלול חישוב מדד או תוצאת ביניים:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
אפס/התחל להקליט מאפס
אם ברצונך להתחיל מחדש לגמרי, השתמש ב- tf.GradientTape.reset . פשוט יציאה מבלוק הטייפ והפעלה מחדש היא בדרך כלל קלה יותר לקריאה, אבל אתה יכול להשתמש בשיטת reset כאשר היציאה מבלוק הטייפ קשה או בלתי אפשרית.
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all the tape recorded so far.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
עצור את זרימת השיפוע בדיוק
בניגוד לפקדי הקלטת הגלובליים לעיל, הפונקציה tf.stop_gradient היא הרבה יותר מדויקת. ניתן להשתמש בו כדי לעצור מעברי מעבר לאורך נתיב מסוים, ללא צורך בגישה לקלטת עצמה:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
מעברי צבע מותאמים אישית
במקרים מסוימים, ייתכן שתרצה לשלוט בדיוק כיצד מחושבים מעברי צבע במקום להשתמש בברירת המחדל. מצבים אלה כוללים:
- אין שיפוע מוגדר עבור ניתוח חדש שאתה כותב.
- חישובי ברירת המחדל אינם יציבים מספרית.
- אתה רוצה לאחסן חישוב יקר מהמעבר קדימה.
- אתה רוצה לשנות ערך (לדוגמה, באמצעות
tf.clip_by_valueאוtf.math.round) מבלי לשנות את הגרדיאנט.
במקרה הראשון, כדי לכתוב אופציה חדשה אתה יכול להשתמש ב- tf.RegisterGradient כדי להגדיר משלך (עיין במסמכי ה-API לפרטים). (שים לב שרישום ההדרגתיות הוא גלובלי, אז שנה אותו בזהירות.)
עבור שלושת המקרים האחרונים, אתה יכול להשתמש ב- tf.custom_gradient .
הנה דוגמה שמחילה את tf.clip_by_norm על שיפוע הביניים:
# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, shape=(), dtype=float32)
עיין במסמכי ה-API של tf.custom_gradient decorator לקבלת פרטים נוספים.
מעברי צבע מותאמים אישית ב- SavedModel
ניתן לשמור מעברי צבע מותאמים אישית ב- SavedModel על ידי שימוש באפשרות tf.saved_model.SaveOptions(experimental_custom_gradients=True) .
כדי להישמר ב-SavedModel, פונקציית הגרדיאנט חייבת להיות ניתנת למעקב (למידע נוסף, עיין במדריך Better Performance with tf.function ).
class MyModule(tf.Module):
@tf.function(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
model = MyModule()
tf.saved_model.save(
model,
'saved_model',
options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
INFO:tensorflow:Assets written to: saved_model/assets tf.Tensor(2.0, shape=(), dtype=float32)
הערה לגבי הדוגמה לעיל: אם תנסה להחליף את הקוד לעיל ב- tf.saved_model.SaveOptions(experimental_custom_gradients=False) , הגרדיאנט עדיין יפיק את אותה תוצאה בטעינה. הסיבה היא שרישום הגרדיאנט עדיין מכיל את הגרדיאנט המותאם אישית המשמש בפונקציה call_custom_op . עם זאת, אם תפעיל מחדש את זמן הריצה לאחר שמירה ללא מעברי צבע מותאמים אישית, הפעלת המודל הנטען תחת ה- tf.GradientTape תגרום לשגיאה: LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .
מספר קלטות
קלטות מרובות פועלות בצורה חלקה.
לדוגמה, כאן כל קלטת צופה בסט אחר של טנסורים:
x0 = tf.constant(0.0)
x1 = tf.constant(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
שיפועים מסדר גבוה יותר
פעולות בתוך מנהל ההקשרים tf.GradientTape נרשמות לצורך בידול אוטומטי. אם שיפועים מחושבים בהקשר זה, חישוב השיפוע נרשם גם כן. כתוצאה מכך, אותו API בדיוק עובד גם עבור מעברי צבע מסדר גבוה יותר.
לדוגמה:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient inside the outer `t2` context manager
# which means the gradient computation is differentiable as well.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0 d2y_dx2: 6.0
אמנם זה נותן לך את הנגזרת השנייה של פונקציה סקלרית , אבל דפוס זה אינו מכליל כדי לייצר מטריצה הסיאנית, מכיוון tf.GradientTape.gradient מחשב רק את הגרדיאנט של סקלאר. כדי לבנות מטריצה הסיאנית , עבור אל הדוגמה ההסיאנית תחת החלק היעקוביאנית .
"קריאות מקוננות ל- tf.GradientTape.gradient " הוא דפוס טוב כאשר אתה מחשב סקלר מדרגת, ואז הסקלר המתקבל פועל כמקור לחישוב שיפוע שני, כמו בדוגמה הבאה.
דוגמה: הסדרת מעברי קלט
דגמים רבים רגישים ל"דוגמאות יריבות". אוסף טכניקות זה משנה את הקלט של המודל כדי לבלבל את הפלט של המודל. היישום הפשוט ביותר - כמו הדוגמה האדוורסרית באמצעות מתקפה של Fast Gradient Signed Method - לוקח צעד אחד לאורך השיפוע של הפלט ביחס לקלט; "שיפוע הקלט".
טכניקה אחת להגברת החוסן לדוגמאות יריבות היא הסדרת שיפוע הקלט (Finlay & Oberman, 2019), המנסה למזער את גודל שיפוע הקלט. אם שיפוע הקלט קטן, אז גם השינוי בפלט צריך להיות קטן.
להלן יישום נאיבי של הסדרת שיפוע קלט. היישום הוא:
- חשב את שיפוע הפלט ביחס לקלט באמצעות סרט פנימי.
- חשב את גודל שיפוע הקלט הזה.
- חשב את השיפוע בגודל זה ביחס למודל.
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The inner tape only takes the gradient with respect to the input,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the input gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the input gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
יעקוביאנים
כל הדוגמאות הקודמות לקחו שיפועים של מטרה סקלרית ביחס לטנסורי מקור מסוימים.
המטריצה היעקוביאנית מייצגת את הגרדיאנטים של פונקציה בעלת ערך וקטור. כל שורה מכילה את הגרדיאנט של אחד מהאלמנטים של הווקטור.
שיטת tf.GradientTape.jacobian מאפשרת לך לחשב ביעילות מטריצה יעקוביאנית.
ציין זאת:
- כמו
gradient: ארגומנטsourcesיכול להיות טנסור או מיכל של טנסור. - בניגוד
gradient: טנסורtargetחייב להיות טנזור בודד.
מקור סקלרי
כדוגמה ראשונה, הנה היעקוביאנית של יעד וקטור ביחס למקור סקלרי.
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
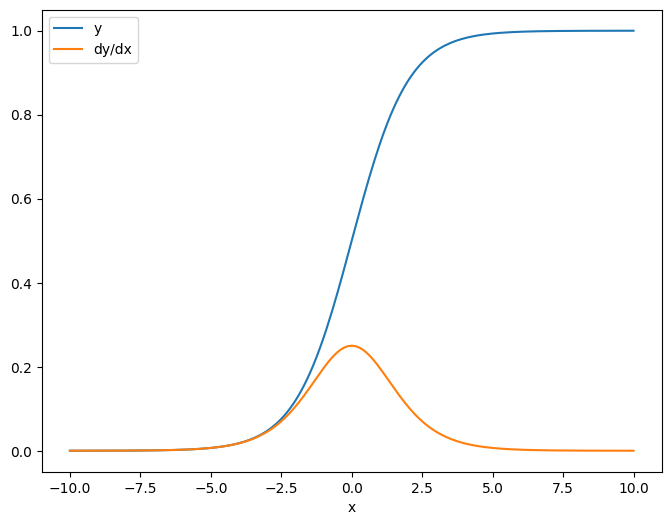
כאשר אתה לוקח את היעקוביאן ביחס לסקלר, לתוצאה יש את הצורה של המטרה , ונותנת את הגרדיאנט של כל אלמנט ביחס למקור:
print(y.shape)
print(dy_dx.shape)
(201,) (201,)
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
מקור טנסור
בין אם הקלט הוא סקלרי או טנזור, tf.GradientTape.jacobian מחשב ביעילות את הגרדיאנט של כל אלמנט של המקור ביחס לכל אלמנט של היעד/ים.
לדוגמה, לפלט של שכבה זו יש צורה של (10, 7) :
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.shape
TensorShape([7, 10])
וצורת הגרעין של השכבה היא (5, 10) :
layer.kernel.shape
TensorShape([5, 10])
צורת היעקוביאנית של הפלט ביחס לגרעין היא שתי הצורות המשורשרות יחד:
j = tape.jacobian(y, layer.kernel)
j.shape
TensorShape([7, 10, 5, 10])
אם אתה מסכם מעל ממדי היעד, אתה נשאר עם שיפוע הסכום שהיה מחושב על ידי tf.GradientTape.gradient :
g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.shape: (5, 10) delta: 2.3841858e-07
דוגמה: הססיאן
בעוד ש- tf.GradientTape לא נותן שיטה מפורשת לבניית מטריצה הסיאנית, אפשר לבנות אחת בשיטת tf.GradientTape.jacobian .
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')
layer.kernel.shape: (5, 8) h.shape: (5, 8, 5, 8)
כדי להשתמש בהסיאן הזה עבור שלב שיטת ניוטון , תחילה תשטח את הצירים שלו למטריצה, ותשטח את הגרדיאנט לוקטור:
n_params = tf.reduce_prod(layer1.kernel.shape)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
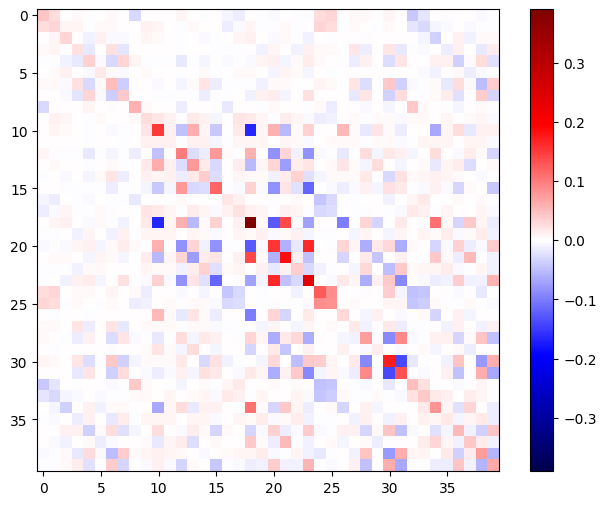
המטריצה ההסיאנית צריכה להיות סימטרית:
def imshow_zero_center(image, **kwargs):
lim = tf.reduce_max(abs(image))
plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
שלב העדכון של שיטת ניוטון מוצג להלן:
eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps
# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)
# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))
אמנם זה פשוט יחסית עבור tf.Variable בודד, אבל יישום זה על מודל לא טריוויאלי ידרוש שרשור ופיזור זהירים כדי לייצר הססיאן מלא על פני מספר משתנים.
אצ' יעקוביאן
במקרים מסוימים, אתה רוצה לקחת את היעקוביאן של כל אחד מערימת מטרות ביחס לערימה של מקורות, כאשר היעקוביאנים עבור כל זוג מטרה-מקור הם עצמאיים.
לדוגמה, כאן הקלט x מעוצב (batch, ins) והפלט y מעוצב (batch, outs) :
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.shape
TensorShape([7, 6])
ליעקוביאן המלא של y ביחס ל- x יש צורה של (batch, ins, batch, outs) , גם אם אתה רוצה רק (batch, ins, outs) :
j = tape.jacobian(y, x)
j.shape
TensorShape([7, 6, 7, 5])
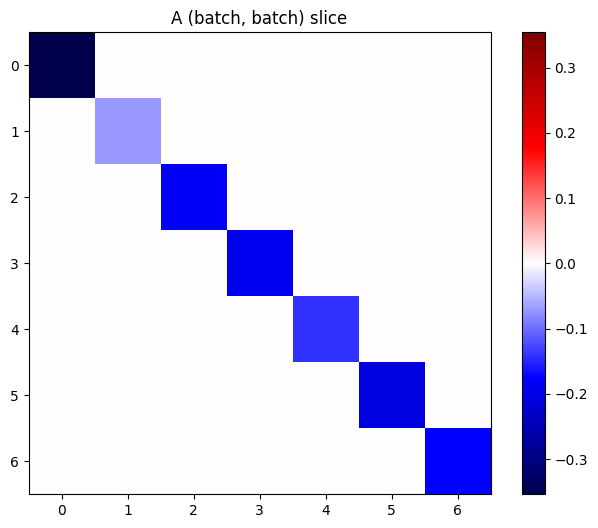
אם ההדרגות של כל פריט בערימה אינן תלויות, אז כל פרוסה (batch, batch) של טנזור זה היא מטריצה אלכסונית:
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
def plot_as_patches(j):
# Reorder axes so the diagonals will each form a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between each patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to form a single image.
s = j.shape
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
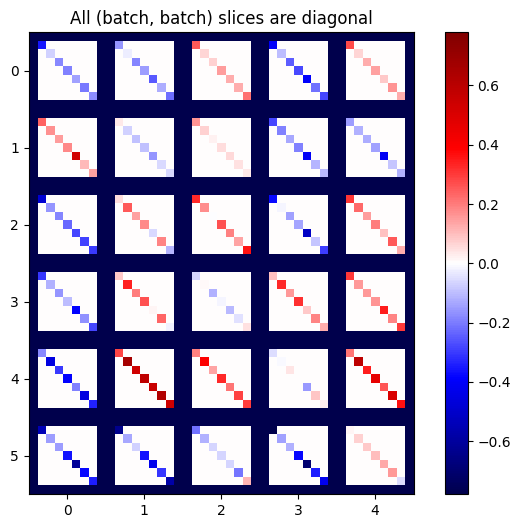
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
כדי לקבל את התוצאה הרצויה, אתה יכול לסכם על ממד batch הכפול, או לבחור באלכסונים באמצעות tf.einsum :
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)
(7, 6, 5) (7, 6, 5)
זה יהיה הרבה יותר יעיל לעשות את החישוב בלי הממד הנוסף מלכתחילה. שיטת tf.GradientTape.batch_jacobian עושה בדיוק את זה:
jb = tape.batch_jacobian(y, x)
jb.shape
WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. TensorShape([7, 6, 5])
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, training=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')
WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. j.shape: (7, 6, 7, 5)
plot_as_patches(j)
_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")
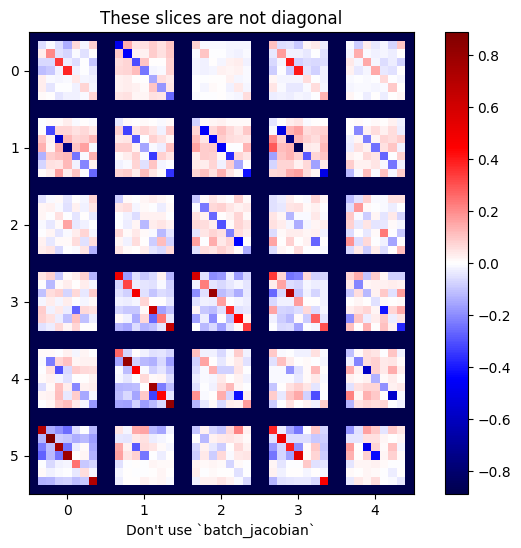
במקרה זה, batch_jacobian עדיין פועל ומחזיר משהו עם הצורה הצפויה, אך לתוכן שלו יש משמעות לא ברורה:
jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')
jb.shape: (7, 6, 5)
