TensorFlow torna al Google I/O il 14 maggio! Iscriviti ora

Questa pagina è stata tradotta dall'API Cloud Translation.

Differenziazione automatica avanzata

Visualizza su TensorFlow.org

Esegui in Google Colab

Visualizza l'origine su GitHub

Scarica quaderno

La guida Introduzione ai gradienti e alla differenziazione automatica include tutto il necessario per calcolare i gradienti in TensorFlow. Questa guida si concentra sulle funzionalità più profonde e meno comuni dell'API tf.GradientTape .

Impostare

import tensorflow as tf

import matplotlib as mpl
import matplotlib.pyplot as plt

mpl.rcParams['figure.figsize'] = (8, 6)

Controllo della registrazione del gradiente

Nella guida alla differenziazione automatica hai visto come controllare quali variabili e tensori vengono osservati dal nastro mentre costruisci il calcolo del gradiente.

Il nastro ha anche metodi per manipolare la registrazione.

Interrompi la registrazione

Se desideri interrompere la registrazione dei gradienti, puoi utilizzare tf.GradientTape.stop_recording per sospendere temporaneamente la registrazione.

Questo può essere utile per ridurre il sovraccarico se non si desidera differenziare un'operazione complicata nel mezzo del modello. Ciò potrebbe includere il calcolo di una metrica o di un risultato intermedio:

x = tf.Variable(2.0)
y = tf.Variable(3.0)

with tf.GradientTape() as t:
  x_sq = x * x
  with t.stop_recording():
    y_sq = y * y
  z = x_sq + y_sq

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

Ripristina/avvia la registrazione da zero

Se desideri ricominciare da capo, usa tf.GradientTape.reset . La semplice uscita dal blocco del nastro del gradiente e il riavvio sono generalmente più facili da leggere, ma è possibile utilizzare il metodo di reset quando l'uscita dal blocco del nastro è difficile o impossibile.

x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True

with tf.GradientTape() as t:
  y_sq = y * y
  if reset:
    # Throw out all the tape recorded so far.
    t.reset()
  z = x * x + y_sq

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

Arresta il flusso del gradiente con precisione

In contrasto con i controlli del nastro globali sopra, la funzione tf.stop_gradient è molto più precisa. Può essere utilizzato per impedire che i gradienti scorrano lungo un determinato percorso, senza dover accedere al nastro stesso:

x = tf.Variable(2.0)
y = tf.Variable(3.0)

with tf.GradientTape() as t:
  y_sq = y**2
  z = x**2 + tf.stop_gradient(y_sq)

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

Sfumature personalizzate

In alcuni casi, potresti voler controllare esattamente come vengono calcolati i gradienti piuttosto che usare l'impostazione predefinita. Queste situazioni includono:

Non esiste un gradiente definito per una nuova operazione che stai scrivendo.
I calcoli predefiniti sono numericamente instabili.
Desideri memorizzare nella cache un calcolo costoso dal passaggio in avanti.
Si desidera modificare un valore (ad esempio, utilizzando tf.clip_by_value o tf.math.round ) senza modificare il gradiente.

Per il primo caso, per scrivere una nuova operazione puoi usare tf.RegisterGradient per configurarne una tua (fare riferimento alla documentazione API per i dettagli). (Nota che il registro del gradiente è globale, quindi modificalo con cautela.)

Per gli ultimi tre casi, puoi usare tf.custom_gradient .

Ecco un esempio che applica tf.clip_by_norm al gradiente intermedio:

# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
  def backward(dy):
    return tf.clip_by_norm(dy, 0.5)
  return y, backward

v = tf.Variable(2.0)
with tf.GradientTape() as t:
  output = clip_gradients(v * v)
print(t.gradient(output, v))  # calls "backward", which clips 4 to 2

tf.Tensor(2.0, shape=(), dtype=float32)

Fare riferimento alla documentazione API del decoratore tf.custom_gradient per maggiori dettagli.

Sfumature personalizzate in SavedModel

I gradienti personalizzati possono essere salvati in SavedModel usando l'opzione tf.saved_model.SaveOptions(experimental_custom_gradients=True) .

Per essere salvata nel SavedModel, la funzione gradiente deve essere tracciabile (per saperne di più, consulta la guida Better performance with tf.function ).

class MyModule(tf.Module):

  @tf.function(input_signature=[tf.TensorSpec(None)])
  def call_custom_grad(self, x):
    return clip_gradients(x)

model = MyModule()

tf.saved_model.save(
    model,
    'saved_model',
    options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))

# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
  output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))

INFO:tensorflow:Assets written to: saved_model/assets
tf.Tensor(2.0, shape=(), dtype=float32)

Una nota sull'esempio precedente: se provi a sostituire il codice sopra con tf.saved_model.SaveOptions(experimental_custom_gradients=False) , il gradiente produrrà comunque lo stesso risultato durante il caricamento. Il motivo è che il registro del gradiente contiene ancora il gradiente personalizzato utilizzato nella funzione call_custom_op . Tuttavia, se si riavvia il runtime dopo aver salvato senza gradienti personalizzati, l'esecuzione del modello caricato in tf.GradientTape genererà l'errore: LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .

Più nastri

Più nastri interagiscono senza problemi.

Ad esempio, qui ogni nastro osserva un diverso insieme di tensori:

x0 = tf.constant(0.0)
x1 = tf.constant(0.0)

with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
  tape0.watch(x0)
  tape1.watch(x1)

  y0 = tf.math.sin(x0)
  y1 = tf.nn.sigmoid(x1)

  y = y0 + y1

  ys = tf.reduce_sum(y)

tape0.gradient(ys, x0).numpy()   # cos(x) => 1.0

1.0

tape1.gradient(ys, x1).numpy()   # sigmoid(x1)*(1-sigmoid(x1)) => 0.25

0.25

Gradienti di ordine superiore

Le operazioni all'interno del gestore di contesto tf.GradientTape vengono registrate per la differenziazione automatica. Se i gradienti vengono calcolati in quel contesto, viene registrato anche il calcolo del gradiente. Di conseguenza, la stessa identica API funziona anche per gradienti di ordine superiore.

Per esempio:

x = tf.Variable(1.0)  # Create a Tensorflow variable initialized to 1.0

with tf.GradientTape() as t2:
  with tf.GradientTape() as t1:
    y = x * x * x

  # Compute the gradient inside the outer `t2` context manager
  # which means the gradient computation is differentiable as well.
  dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)

print('dy_dx:', dy_dx.numpy())  # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy())  # 6 * x => 6.0

dy_dx: 3.0
d2y_dx2: 6.0

Sebbene ciò ti dia la derivata seconda di una funzione scalare , questo modello non si generalizza per produrre una matrice dell'Assia, poiché tf.GradientTape.gradient calcola solo il gradiente di uno scalare. Per costruire una matrice dell'Assia , passare all'esempio dell'Assia nella sezione giacobina .

"Chiamate nidificate a tf.GradientTape.gradient " è un buon modello quando si calcola uno scalare da un gradiente, quindi lo scalare risultante funge da origine per un secondo calcolo del gradiente, come nell'esempio seguente.

Esempio: regolarizzazione del gradiente di input

Molti modelli sono suscettibili di "esempi contraddittori". Questa raccolta di tecniche modifica l'input del modello per confondere l'output del modello. L'implementazione più semplice, come l' esempio Adversarial che utilizza l'attacco Fast Gradient Signed Method, esegue un singolo passaggio lungo il gradiente dell'output rispetto all'input; il "gradiente di input".

Una tecnica per aumentare la robustezza degli esempi contraddittori è la regolarizzazione del gradiente di input (Finlay & Oberman, 2019), che tenta di ridurre al minimo l'entità del gradiente di input. Se il gradiente di input è piccolo, anche la modifica nell'output dovrebbe essere piccola.

Di seguito è riportata un'implementazione ingenua della regolarizzazione del gradiente di input. L'implementazione è:

Calcolare il gradiente dell'output rispetto all'input utilizzando un nastro interno.
Calcola la grandezza di quel gradiente di input.
Calcola il gradiente di quella grandezza rispetto al modello.

x = tf.random.normal([7, 5])

layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)

with tf.GradientTape() as t2:
  # The inner tape only takes the gradient with respect to the input,
  # not the variables.
  with tf.GradientTape(watch_accessed_variables=False) as t1:
    t1.watch(x)
    y = layer(x)
    out = tf.reduce_sum(layer(x)**2)
  # 1. Calculate the input gradient.
  g1 = t1.gradient(out, x)
  # 2. Calculate the magnitude of the input gradient.
  g1_mag = tf.norm(g1)

# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)

[var.shape for var in dg1_mag]

[TensorShape([5, 10]), TensorShape([10])]

giacobini

Tutti gli esempi precedenti hanno preso i gradienti di un target scalare rispetto ad alcuni tensori di origine.

La matrice Jacobiana rappresenta i gradienti di una funzione con valori vettoriali. Ogni riga contiene il gradiente di uno degli elementi del vettore.

Il metodo tf.GradientTape.jacobian consente di calcolare in modo efficiente una matrice Jacobiana.

Notare che:

Like gradient : l'argomento delle sources può essere un tensore o un contenitore di tensori.
A differenza gradient : il tensore target deve essere un singolo tensore.

Sorgente scalare

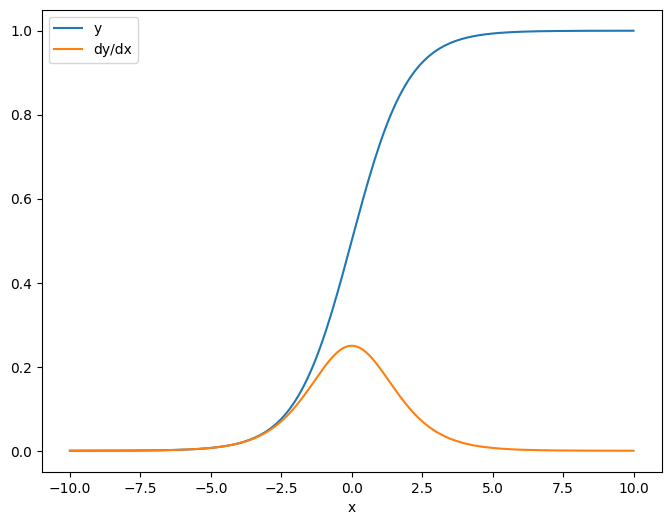
Come primo esempio, ecco lo Jacobiano di un vettore-bersaglio rispetto a una sorgente scalare.

x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)

with tf.GradientTape() as tape:
  y = tf.nn.sigmoid(x+delta)

dy_dx = tape.jacobian(y, delta)

Quando prendi lo Jacobiano rispetto a uno scalare il risultato ha la forma del target e fornisce il gradiente di ciascun elemento rispetto alla sorgente:

print(y.shape)
print(dy_dx.shape)

(201,)
(201,)

plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')

png

Sorgente tensoriale

Indipendentemente dal fatto che l'input sia scalare o tensore, tf.GradientTape.jacobian calcola in modo efficiente il gradiente di ciascun elemento della sorgente rispetto a ciascun elemento dei target.

Ad esempio, l'output di questo livello ha una forma di (10, 7) :

x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)

with tf.GradientTape(persistent=True) as tape:
  y = layer(x)

y.shape

TensorShape([7, 10])

E la forma del kernel del livello è (5, 10) :

layer.kernel.shape

TensorShape([5, 10])

La forma dello Jacobiano dell'output rispetto al kernel è quella di queste due forme concatenate insieme:

j = tape.jacobian(y, layer.kernel)
j.shape

TensorShape([7, 10, 5, 10])

Se sommi le dimensioni del target, ti rimane il gradiente della somma che sarebbe stata calcolata da tf.GradientTape.gradient :

g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)

j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)

g.shape: (5, 10)
delta: 2.3841858e-07

Esempio: Assia

Sebbene tf.GradientTape non fornisca un metodo esplicito per costruire una matrice dell'Assia, è possibile costruirne una usando il metodo tf.GradientTape.jacobian .

x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)

with tf.GradientTape() as t2:
  with tf.GradientTape() as t1:
    x = layer1(x)
    x = layer2(x)
    loss = tf.reduce_mean(x**2)

  g = t1.gradient(loss, layer1.kernel)

h = t2.jacobian(g, layer1.kernel)

print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')

layer.kernel.shape: (5, 8)
h.shape: (5, 8, 5, 8)

Per utilizzare questa iuta per un passaggio del metodo di Newton , devi prima appiattire i suoi assi in una matrice e appiattire il gradiente in un vettore:

n_params = tf.reduce_prod(layer1.kernel.shape)

g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])

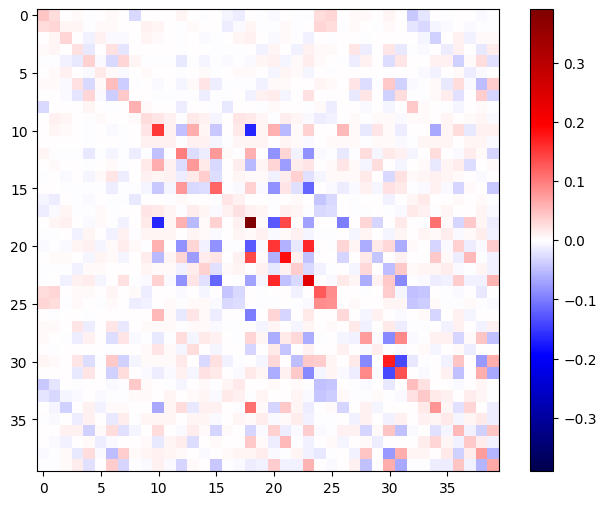
La matrice dell'Assia dovrebbe essere simmetrica:

def imshow_zero_center(image, **kwargs):
  lim = tf.reduce_max(abs(image))
  plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
  plt.colorbar()

imshow_zero_center(h_mat)

png

Il passaggio di aggiornamento del metodo di Newton è mostrato di seguito:

eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps

# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)

# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))

Sebbene ciò sia relativamente semplice per un singolo tf.Variable , applicarlo a un modello non banale richiederebbe un'attenta concatenazione e affettatura per produrre un'intera iuta su più variabili.

Lotto giacobino

In alcuni casi, si desidera prendere lo Jacobiano di ciascuno di uno stack di target rispetto a uno stack di origini, in cui gli Jacobiani per ciascuna coppia target-source sono indipendenti.

Ad esempio, qui l'input x è sagomato (batch, ins) e l'output y è sagomato (batch, outs) :

x = tf.random.normal([7, 5])

layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)

with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
  tape.watch(x)
  y = layer1(x)
  y = layer2(y)

y.shape

TensorShape([7, 6])

Il Jacobiano completo di y rispetto a x ha una forma di (batch, ins, batch, outs) , anche se vuoi solo (batch, ins, outs) :

j = tape.jacobian(y, x)
j.shape

TensorShape([7, 6, 7, 5])

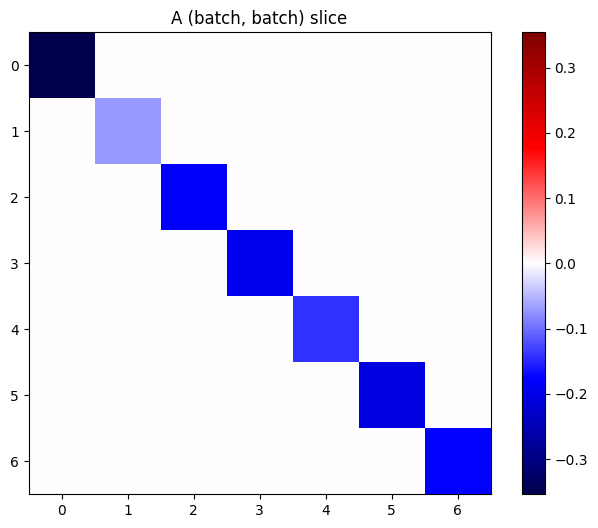
Se i gradienti di ogni elemento nella pila sono indipendenti, allora ogni sezione (batch, batch) di questo tensore è una matrice diagonale:

imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')

png

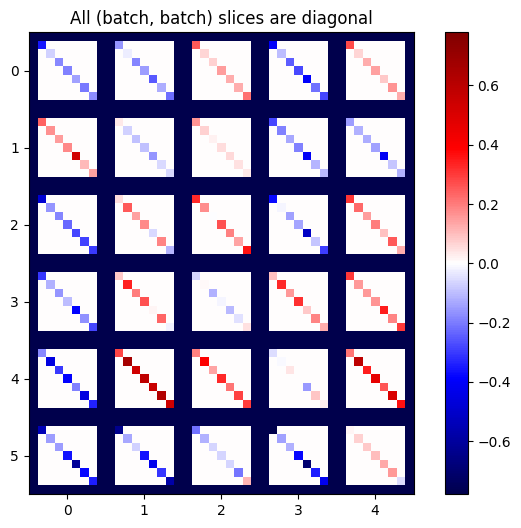
def plot_as_patches(j):
  # Reorder axes so the diagonals will each form a contiguous patch.
  j = tf.transpose(j, [1, 0, 3, 2])
  # Pad in between each patch.
  lim = tf.reduce_max(abs(j))
  j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
             constant_values=-lim)
  # Reshape to form a single image.
  s = j.shape
  j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
  imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])

plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')

png

Per ottenere il risultato desiderato, puoi sommare la dimensione batch duplicata, oppure selezionare le diagonali usando tf.einsum :

j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)

(7, 6, 5)
(7, 6, 5)

Sarebbe molto più efficiente eseguire il calcolo senza la dimensione extra in primo luogo. Il metodo tf.GradientTape.batch_jacobian fa esattamente questo:

jb = tape.batch_jacobian(y, x)
jb.shape

WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.
TensorShape([7, 6, 5])

error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())

0.0

x = tf.random.normal([7, 5])

layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)

with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
  tape.watch(x)
  y = layer1(x)
  y = bn(y, training=True)
  y = layer2(y)

j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')

WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.
j.shape: (7, 6, 7, 5)

plot_as_patches(j)

_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")

png

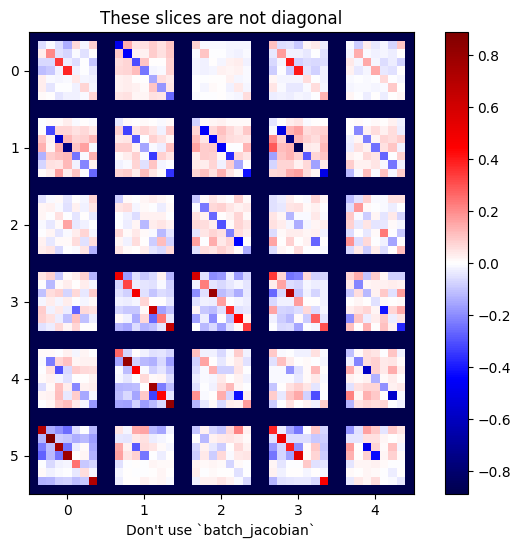
In questo caso, batch_jacobian viene ancora eseguito e restituisce qualcosa con la forma prevista, ma il suo contenuto ha un significato poco chiaro:

jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')

jb.shape: (7, 6, 5)