 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запустить в Google Colab Запустить в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
Руководство « Введение в градиенты и автоматическую дифференциацию » включает в себя все необходимое для расчета градиентов в TensorFlow. Это руководство фокусируется на более глубоких, менее распространенных функциях API tf.GradientTape .
Настраивать
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.figsize'] = (8, 6)
Управление записью градиента
В руководстве по автоматическому дифференцированию вы видели, как контролировать, какие переменные и тензоры отслеживаются лентой при построении вычисления градиента.
На ленте также есть методы управления записью.
Остановить запись
Если вы хотите остановить запись градиентов, вы можете использовать tf.GradientTape.stop_recording , чтобы временно приостановить запись.
Это может быть полезно для уменьшения накладных расходов, если вы не хотите выделять сложную операцию в середине вашей модели. Это может включать расчет метрики или промежуточного результата:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
x_sq = x * x
with t.stop_recording():
y_sq = y * y
z = x_sq + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Сбросить/начать запись с нуля
Если вы хотите начать все сначала, используйте tf.GradientTape.reset . Простой выход из блока ленты градиента и перезапуск обычно легче читаются, но вы можете использовать метод reset , когда выход из блока ленты затруднен или невозможен.
x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True
with tf.GradientTape() as t:
y_sq = y * y
if reset:
# Throw out all the tape recorded so far.
t.reset()
z = x * x + y_sq
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Остановите поток градиента с точностью
В отличие от глобальных элементов управления лентой, описанных выше, функция tf.stop_gradient намного точнее. Его можно использовать для остановки прохождения градиентов по определенному пути без необходимости доступа к самой ленте:
x = tf.Variable(2.0)
y = tf.Variable(3.0)
with tf.GradientTape() as t:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = t.gradient(z, {'x': x, 'y': y})
print('dz/dx:', grad['x']) # 2*x => 4
print('dz/dy:', grad['y'])
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32) dz/dy: None
Пользовательские градиенты
В некоторых случаях вы можете захотеть точно контролировать, как рассчитываются градиенты, а не использовать значение по умолчанию. К таким ситуациям относятся:
- Для новой операции, которую вы пишете, не существует определенного градиента.
- Расчеты по умолчанию численно нестабильны.
- Вы хотите кэшировать дорогостоящие вычисления из прямого прохода.
- Вы хотите изменить значение (например, используя
tf.clip_by_valueилиtf.math.round) без изменения градиента.
В первом случае, чтобы написать новую операцию, вы можете использовать tf.RegisterGradient для настройки своей собственной (подробности см. в документации по API). (Обратите внимание, что реестр градиентов является глобальным, поэтому меняйте его с осторожностью.)
Для последних трех случаев вы можете использовать tf.custom_gradient .
Вот пример применения tf.clip_by_norm к промежуточному градиенту:
# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
def backward(dy):
return tf.clip_by_norm(dy, 0.5)
return y, backward
v = tf.Variable(2.0)
with tf.GradientTape() as t:
output = clip_gradients(v * v)
print(t.gradient(output, v)) # calls "backward", which clips 4 to 2
tf.Tensor(2.0, shape=(), dtype=float32)
Дополнительные сведения см. в документации по API декоратора tf.custom_gradient .
Пользовательские градиенты в SavedModel
Пользовательские градиенты можно сохранить в SavedModel с помощью параметра tf.saved_model.SaveOptions(experimental_custom_gradients=True) .
Чтобы быть сохраненной в SavedModel, функция градиента должна быть отслеживаемой (чтобы узнать больше, ознакомьтесь с руководством по повышению производительности с помощью tf.function ).
class MyModule(tf.Module):
@tf.function(input_signature=[tf.TensorSpec(None)])
def call_custom_grad(self, x):
return clip_gradients(x)
model = MyModule()
tf.saved_model.save(
model,
'saved_model',
options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))
# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))
INFO:tensorflow:Assets written to: saved_model/assets tf.Tensor(2.0, shape=(), dtype=float32)
Примечание к приведенному выше примеру: если вы попытаетесь заменить приведенный выше код на tf.saved_model.SaveOptions(experimental_custom_gradients=False) , градиент по-прежнему будет давать тот же результат при загрузке. Причина в том, что реестр градиентов по-прежнему содержит пользовательский градиент, используемый в функции call_custom_op . Однако, если вы перезапустите среду выполнения после сохранения без пользовательских градиентов, запуск загруженной модели под tf.GradientTape вызовет ошибку: LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .
Несколько лент
Несколько лент взаимодействуют без проблем.
Например, здесь каждая лента отслеживает разные наборы тензоров:
x0 = tf.constant(0.0)
x1 = tf.constant(0.0)
with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
tape0.watch(x0)
tape1.watch(x1)
y0 = tf.math.sin(x0)
y1 = tf.nn.sigmoid(x1)
y = y0 + y1
ys = tf.reduce_sum(y)
tape0.gradient(ys, x0).numpy() # cos(x) => 1.0
1.0
tape1.gradient(ys, x1).numpy() # sigmoid(x1)*(1-sigmoid(x1)) => 0.25
0.25
Градиенты высшего порядка
Операции внутри менеджера контекста tf.GradientTape записываются для автоматической дифференциации. Если градиенты вычисляются в этом контексте, то вычисление градиента также записывается. В результате тот же самый API работает и для градиентов более высокого порядка.
Например:
x = tf.Variable(1.0) # Create a Tensorflow variable initialized to 1.0
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
y = x * x * x
# Compute the gradient inside the outer `t2` context manager
# which means the gradient computation is differentiable as well.
dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)
print('dy_dx:', dy_dx.numpy()) # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy()) # 6 * x => 6.0
dy_dx: 3.0 d2y_dx2: 6.0
Хотя это дает вам вторую производную скалярной функции, этот шаблон не обобщается для создания матрицы Гессе, поскольку tf.GradientTape.gradient вычисляет только градиент скаляра. Чтобы построить матрицу Гессе , перейдите к примеру Гессе в разделе Якобиана .
«Вложенные вызовы tf.GradientTape.gradient » — хороший шаблон, когда вы вычисляете скаляр из градиента, а затем результирующий скаляр действует как источник для второго вычисления градиента, как в следующем примере.
Пример: регуляризация входного градиента
Многие модели восприимчивы к «состязательным примерам». Этот набор методов изменяет входные данные модели, чтобы запутать выходные данные модели. Простейшая реализация, такая как пример Adversarial с использованием атаки Fast Gradient Signed Method , делает один шаг по градиенту выходных данных по отношению к входным; «входной градиент».
Одним из методов повышения устойчивости к враждебным примерам является регуляризация входного градиента (Finlay & Oberman, 2019), которая пытается минимизировать величину входного градиента. Если входной градиент мал, то и выходное изменение должно быть небольшим.
Ниже представлена наивная реализация регуляризации входного градиента. Реализация:
- Вычислите градиент выхода по отношению к входу, используя внутреннюю ленту.
- Вычислите величину этого входного градиента.
- Вычислите градиент этой величины по отношению к модели.
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape() as t2:
# The inner tape only takes the gradient with respect to the input,
# not the variables.
with tf.GradientTape(watch_accessed_variables=False) as t1:
t1.watch(x)
y = layer(x)
out = tf.reduce_sum(layer(x)**2)
# 1. Calculate the input gradient.
g1 = t1.gradient(out, x)
# 2. Calculate the magnitude of the input gradient.
g1_mag = tf.norm(g1)
# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)
[var.shape for var in dg1_mag]
[TensorShape([5, 10]), TensorShape([10])]
якобианцы
Во всех предыдущих примерах использовались градиенты скалярной цели относительно некоторого исходного тензора (тензоров).
Матрица Якоби представляет градиенты векторной функции. Каждая строка содержит градиент одного из элементов вектора.
Метод tf.GradientTape.jacobian позволяет эффективно вычислять матрицу Якоби.
Обратите внимание, что:
- Подобно
gradient: аргументsourcesможет быть тензором или контейнером тензоров. - В отличие от
gradient:targetтензор должен быть одним тензором.
Скалярный источник
В качестве первого примера, вот якобиан вектора-цели относительно скаляра-источника.
x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)
with tf.GradientTape() as tape:
y = tf.nn.sigmoid(x+delta)
dy_dx = tape.jacobian(y, delta)
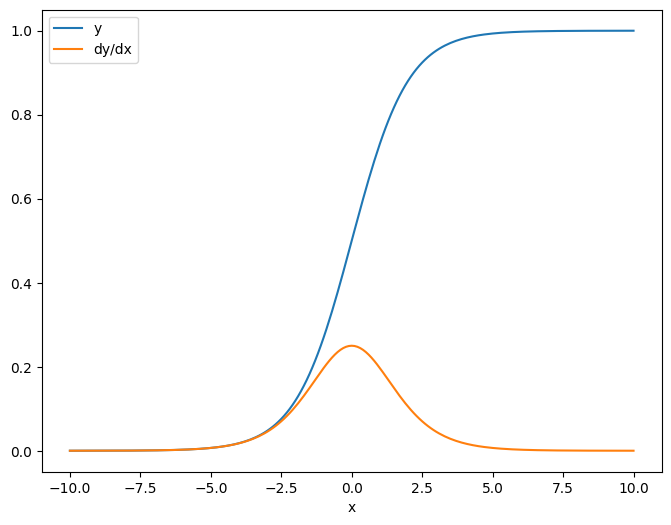
Когда вы берете якобиан по отношению к скаляру, результат имеет форму цели и дает градиент каждого элемента по отношению к источнику:
print(y.shape)
print(dy_dx.shape)
(201,) (201,)
plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')
Источник тензора
Независимо от того, являются ли входные данные скалярными или тензорными, tf.GradientTape.jacobian эффективно вычисляет градиент каждого элемента источника по отношению к каждому элементу цели (целей).
Например, выходные данные этого слоя имеют форму (10, 7) :
x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)
with tf.GradientTape(persistent=True) as tape:
y = layer(x)
y.shape
TensorShape([7, 10])
И форма ядра слоя (5, 10) :
layer.kernel.shape
TensorShape([5, 10])
Форма якобиана выходных данных по отношению к ядру - это эти две формы, объединенные вместе:
j = tape.jacobian(y, layer.kernel)
j.shape
TensorShape([7, 10, 5, 10])
Если вы просуммируете размеры цели, у вас останется градиент суммы, который был бы рассчитан tf.GradientTape.gradient :
g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)
j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)
g.shape: (5, 10) delta: 2.3841858e-07
Пример: Гессен
Хотя tf.GradientTape не дает явного метода построения матрицы Гессе, ее можно построить с помощью метода tf.GradientTape.jacobian .
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)
with tf.GradientTape() as t2:
with tf.GradientTape() as t1:
x = layer1(x)
x = layer2(x)
loss = tf.reduce_mean(x**2)
g = t1.gradient(loss, layer1.kernel)
h = t2.jacobian(g, layer1.kernel)
print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')
layer.kernel.shape: (5, 8) h.shape: (5, 8, 5, 8)
Чтобы использовать этот гессиан для шага метода Ньютона , вы должны сначала сгладить его оси в матрицу и сгладить градиент в вектор:
n_params = tf.reduce_prod(layer1.kernel.shape)
g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])
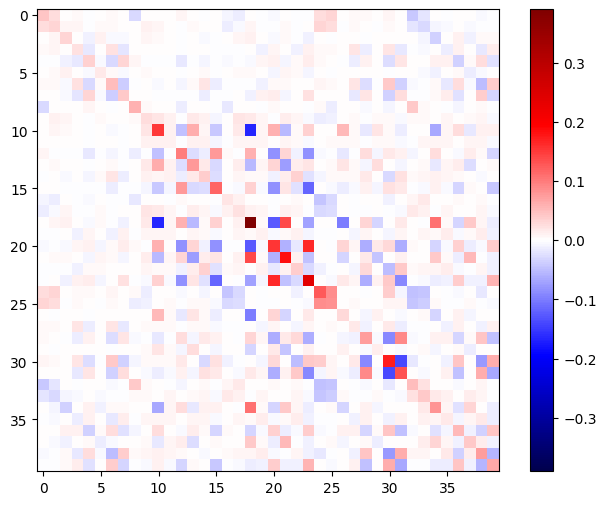
Матрица Гессе должна быть симметричной:
def imshow_zero_center(image, **kwargs):
lim = tf.reduce_max(abs(image))
plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
plt.colorbar()
imshow_zero_center(h_mat)
Шаг обновления метода Ньютона показан ниже:
eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps
# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)
# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))
Хотя это относительно просто для одной tf.Variable , применение этого к нетривиальной модели потребует тщательной конкатенации и разделения для получения полного гессиана по нескольким переменным.
Пакетный якобиан
В некоторых случаях вы хотите взять якобиан каждого из стека целей по отношению к стеку источников, где якобианы для каждой пары цель-источник независимы.
Например, здесь вход x сформирован (batch, ins) а выход y сформирован (batch, outs) :
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = layer2(y)
y.shape
TensorShape([7, 6])
Полный якобиан y по отношению к x имеет вид (batch, ins, batch, outs) , даже если вы хотите только (batch, ins, outs) :
j = tape.jacobian(y, x)
j.shape
TensorShape([7, 6, 7, 5])
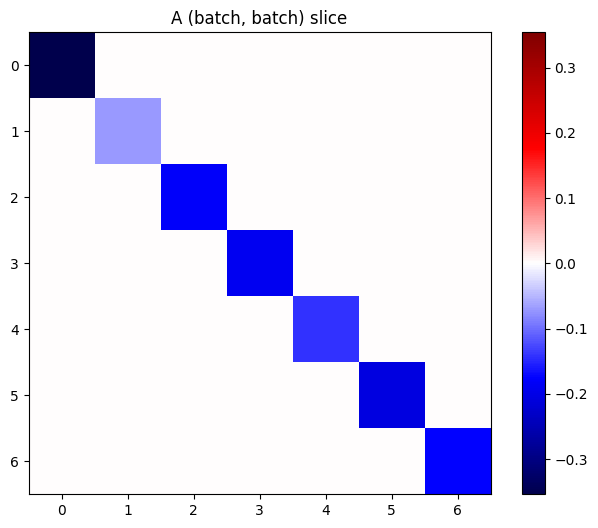
Если градиенты каждого элемента в стеке независимы, то каждый (batch, batch) срез этого тензора представляет собой диагональную матрицу:
imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')
def plot_as_patches(j):
# Reorder axes so the diagonals will each form a contiguous patch.
j = tf.transpose(j, [1, 0, 3, 2])
# Pad in between each patch.
lim = tf.reduce_max(abs(j))
j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
constant_values=-lim)
# Reshape to form a single image.
s = j.shape
j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])
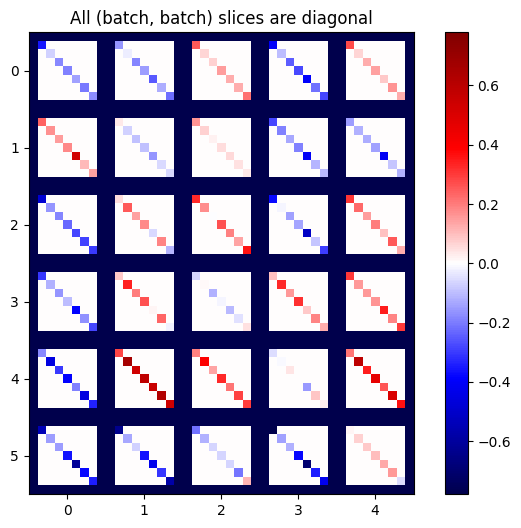
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')
Чтобы получить желаемый результат, вы можете просуммировать повторяющееся измерение batch или выбрать диагонали с помощью tf.einsum :
j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)
(7, 6, 5) (7, 6, 5)
Во-первых, было бы намного эффективнее выполнить расчет без дополнительного измерения. Метод tf.GradientTape.batch_jacobian делает именно это:
jb = tape.batch_jacobian(y, x)
jb.shape
WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. TensorShape([7, 6, 5])
error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())
0.0
x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)
with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
tape.watch(x)
y = layer1(x)
y = bn(y, training=True)
y = layer2(y)
j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')
WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. j.shape: (7, 6, 7, 5)
plot_as_patches(j)
_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")
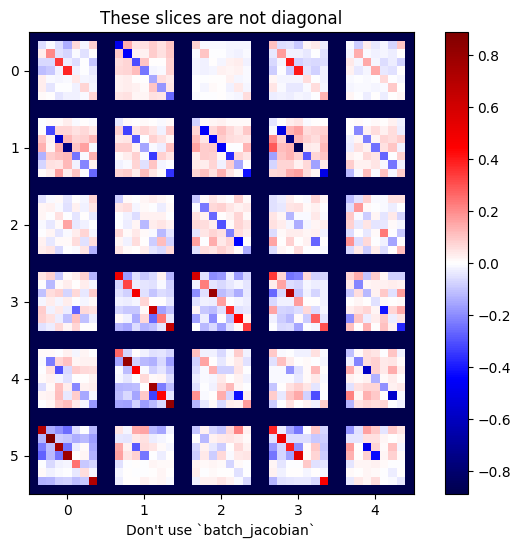
В этом случае batch_jacobian все равно запускается и возвращает что- то с ожидаемой формой, но его содержимое имеет неясный смысл:
jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')
jb.shape: (7, 6, 5)
